LASERII CU GROPI CUANTICE

Universitatea "Politehnica" Bucuresti

Facultatea "Electronica, Telecomunicatii si Tehnologia Informatiei"

LASERII CU GROPI CUANTICE

I.          Introducere

II.       Densitatea de stari intr-un cristal semiconductor

III.   Fenomene de absorbtie in gropi cuantice

III.1. Absorbtia fundamentala in gropi cuantice

III.2. Electroabsorbtia in gropi cuantice

IV.    Tipuri de laseri

IV. 1.    Laserii cu structuri mezoscopice

IV. 2. Laserii cu gropi cuantice multiple

V.       Fire cuantice semiconductoare

VI.    Concluzii

I.          Introducere

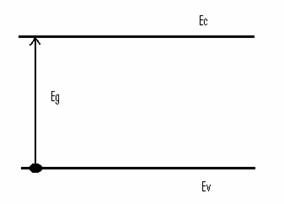
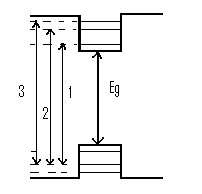
Intr-un cristal de semiconductor, electronii pot ocupa o stare intr-una din cele benzile energetice. Cele mai importante si asupra carora se focalizeaza interesul sunt benzile energetice superioare, banda de valenta si banda de conductie. Banda de valenta, care este populata ( din plin) de electronii de joasa energie si banda de conductie care este populata de electronii cu energii mari. Cele 2 benzii energetice sunt separate de o banda energetica interzisa, banda in care nu exista stari permise valabile pentru care electronul sa le ocupe.

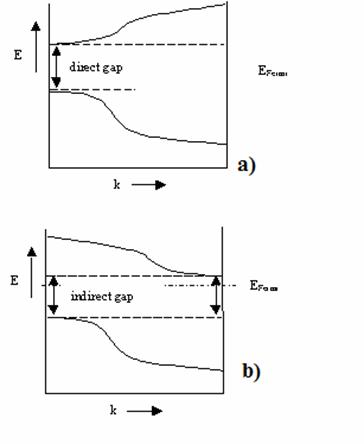Semiconductorii pot fi impartiti in 2 categorii in functie de diferenta energetica dintre cele 2 benzi, si anume semiconductori cu gap direct, in care maximul energetic al benzii de valenta este situat la aceeasi valoare a vectorului de unda ca si minimul benzii de conductie. In acest caz tranzitiile cu absorbtie de foton sunt verticale. Semiconductorii care prezinta minimul benzii de conductie si maximul benzii de valenta situate la puncte diferite se numesc semiconductori cu gap indirect, tranzitiile din banda de valenta in banda de conductie (prin absorbtie de foton) se produce numai cu participare de fonon

(absorbtie sau emisie). Astfel procesele cu participare de fonon fiind procese multiparticula sunt mai putin probabil decat procesele numai cu participare de foton, din acest motiv se prefera utilizarea semiconductorilor cu gap direct in dispozitivele optoelectronice.

Fig 1 Schema energetica a semiconductorilor cu a) gap direct si b)gap indirect

Laserele conventionale pe semiconductorii se bazeaza pe emisia unui foton de catre un electron, la trecerea acestuia din banda de conductie in banda de valenta. Astfel, lungimea de unda a fotonului depinde puternic de banda interzisa a materialului semiconductor.

O groapa cuantica este o groapa de potential, care confera particulei, care se misca liber in spatiul tridimensional, sa se miste liber numai pe 2 directii, obligand-o sa se miste intr-o regiune planara. Aceste efecte de confinare au loc atunci cand grosimea gropii cuantice este comparabila cu lungimea de unda de Broglie asociata carausului (de obicei electron sau gol ), ducand la nivele energetice , numite nivele de subbanda (adica purtatorii pot avea numai nivele discrete de energie).

Aceste heterostructuri sunt formate din "semiconductori grei" (GaAs) care se afla intr-o structura de tip sandwich, celelalte 2 perechi fiind facute din AlGaAs (care prezinta o diferenta de energie intre benzile de conductie si de valenta diferita de cea a GaAs, astfel creandu-se groapa de potential). Aceste structuri pot fii create utilizand epitaxia cu fascicul molecular sau depunere cu vapori chimici, controland astfel grosimea stratului molecular, ajungand la state monoatomice.

II.       Densitatea de stari intr-un cristal semiconductor

Datorita dualitatii sale, electronii din gropile cuantice au o densitate de stari mai mare decat a materialelor obisnuite. De aceea gropile cuantice sunt des folosite in constructia led-urilor, a diodelor laser sau a altor aplicatii optoelectronice (de ex. Celulele fotovoltaice) . De asemenea sunt folositi in fabricarea tranzistoarelor cu electroni de inalta mobilitate (HEMT's High Electrons Mobility Transistors). Fotodetectorii in infrarosu sunt de asemenea bazati pe gropi cuantice.

Pentru determinarea proprietatilor dispozitivelor realizate cu aceste structuri, trebuiesc cunoscute nivelele energetice caracteristice si densitatea de stari .

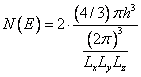Astfel in cazul 3D se stie ca in spatiul dual al vectorilor de unda fiecarei stari a lui ii revine un paralelipiped, cu latura . Energia este iar numarul de electroni cu energia mai mica decat este: , factorul 2 aparand degenerarii datorata spinului, iar numarul de stari este: .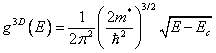

Fig 2.1 Densitatea de stari pentru un cristal 3D

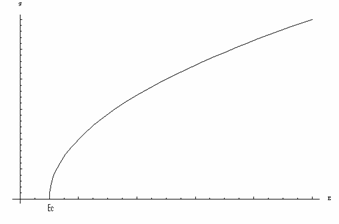
In cazul unei miscari intr-o groapa cuantica, energia este o functie de tipul , numarul de electroni cu energia mai mica decat o energie este si densitatea de stari este de tipul .

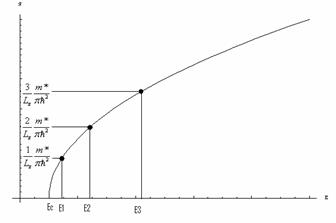
Fig Densitatea de stari pentru o groapa cuantica

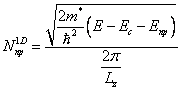Pentru un fir cuantic calculele sunt mult mai laborioase, energia este data de , numarul de electroni si .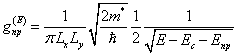

Laserii cu structuri mezoscopice sunt structuri cu dimensionalitate redusa - gropi cuantice, fire cuantice puncte cuantice. Laserii cu gropi cuantice prezinta o serie de avantaje si anume: dimensiuni foarte mici ale zonei active, spectrul radiatiei laser depinde de densitatea de stari din benzile de conductie si valenta. Aceasta densitate de stari, care variaza parabolic cu energia in semiconductorul 3D, au un spectru foarte bine localizat in jurul unor energii discrete (corespunzatoare unor stari stationare) in structurile cu dimensionalitate redusa. Localizarea densitatii de stari in jurul unor energii ofera o crestere a coeficientului de amplificare . De asemenea pierderile prin procese neradiative sunt mici, valorile curentului de prag este mai mic, care de altfel variaza slab cu temperatura. Laserii cu structuri mezoscopice prezinta o banda larga de modulatie in frecventa.

Totusi puterea emisa de acesti laseri este mai mica decat in cazul laserilor cu jonctiuni pentru ca numarul de purtatori implicati in tranzitii este mai mic. Cresterea coeficientului de amplificare , a densitatii de curent de prag si respectiv a largimii benzii de modulatie in laserii cu structuri mezoscopice, fata de aceeasi parametrii in jonctiunile (alesi ca unitate) este data in tabelul 2.1, astfel incat sa fie mai mare decat pierderile interne.

Tabelul 2.1

III.   Fenomene de absorbtie in gropi cuantice

Absorbtia fundamentala in gropi cuantice

Tinand cont ca in anumite conditii intre electroni si goluri pot aparea interactii atractive, de tip coulombiene, avand ca rezultat formarea unei stari legate stabile ale perechii electron- gol, stare ce se numeste exciton. Calculele se pot face prin doua metode:

a)          neglijand excitonii

In semiconductorii 3D tranzitiile din banda de valenta in banda de conductie cu absorbtie de fotoni sunt verticale in spatiul .

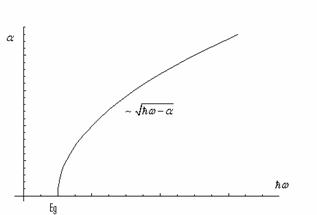
Tranzitiile cu absorbtie in spatiul sunt verticale

Pentru gropi cuantice, pentru directia de crestere , in loc de conservarea vectorului de unda, apare o noua regula de selectie si anume sunt permise numai tranzitiile intre nivelele de energie cu acelasi numar cuantic principal. De altfel aceasta regula este verificata riguros in cazul gropii infinite, probabilitatea de tranzitie din starea initiala in starea finala este proportionala cu integrala de suprapunere intre functiile Bloch corespunzatoare starilor initiale si finale. Aceasta integrala este nenula numai pentru functii de aceeasi paritate. Regula se verifica suficient de bine si pentru gropi finite, integrala de suprapunere avand valori apreciabile numai pentru . 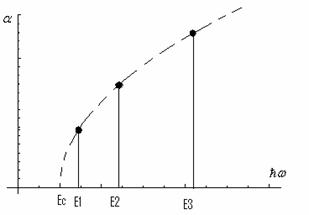In structurile reale nu exista nivele discrete de energie, ci subbenzi" care incep de la energiile calculate pentru starile localizate. Electronul (sau golul) intr-o astfel de stare localizata poate avea orice valoare pentru energia cinetica "in plan" (planul ) si prin urmare un spectru continuu de energii (energia de subbanda) deci densitatea de stari pentru o groapa de potential finita prezinta "trepte" care incep la energiile discrete . In tranzitiile optice se conserva vectorul de unda si pentru ca forma curbei de absorbtie este determinata de cea a densitatii de stari, spectrul de absorbtie este in trepte, cate o treapta pentru fiecare numar cuantic .

Regula de selectie: si conservarea

b)          cu efectele excitonilor

Pentru un cristal de GaAs energia de legatura a unui exciton este de aproximativ de astfel incat energia fotonului absorbit este . Efectele excitonice apar in majoritatea semiconductorilor 3D cu banda interzisa directa, la temperaturi scazute . La temperatura camerei, desi efectele excitonice sunt inca importante, maximile corespunzatoare din curba de absorbtie sunt greu de observat. Motivul este ionizarea excitonilor prin ciocniri cu fononi optici. Aceste procese de ciocniri sunt rapide, astfel incat timpul de viata al unui exciton este scurt si conform principiului de incertitudine al lui Heisenberg largimea liniei spectrale este mare. Prin urmare linia corespunzatoare absorbtiei excitonice nu poate fi distinsa ca o rezonanta clara. Comparativ cu semiconductorii 3D, in cazul unei gropi cuantice apar 2 diferente importante. In cristalul de GaAs diametrul excitonului este de . Intr-o groapa cuantica cu dimensiunea excitonului se reduce, cel putin dupa directia gropii de potential. Este de remarcat faptul ca dimensiunile se reduc si pe celelalte 2 directii. Astfel distanta relativa electron- gol este mult mai mica decat in cazul 3D, atunci coeficientul de absorbtie care este proportional cu integrala de suprapunere intre functiile de unda asociate celor 2 particule este mai mare. De asemenea energia de legatura a excitonului (data de atractia coulombiana ) este mai mare decat in semiconductorul 3D si viteza pe orbita este mai mare (modelul Bohr). Ca urmare, excitonul poate descrie o orbita completa inainte de a absoarbe fononul optic si va exista o rezonanta bine definita. Echivalent se poate spune ca desi largimea liniei excitonice este comparabila cu cea din cazul 3D, energia de legatura in cazul unei gropi cuantice este mai mare si linia excitonica poate fi observata distinctiv in curba de absorbtie din vecinatatea lui . Asa se explica de ce, chiar la temperatura camerei, efectele excitonice sunt importante in cazul "quantum well

Se defineste un coeficient de castig (amplificare) in mediu, ca variatia relativa a intensitatii pe unitatea de lungime , determinat de rata de emisie stimulata. El este pozitiv daca este realizata inversia de populatie. Aceasta conditie este necesara, dar nu si suficienta pentru a obtine amplificarea radiatiei. Acest termen trebuie sa fie nu numai pozitiv ci si mai mare decat pierderile. In laserii cu semiconductori aceste pierderi sunt legate de faptul ca un electron din banda de conductie avand energia poate absorbi radiatia de energie pentru a trece in starea de energie . Acest fenomen este cunoscut sub numele de efect Auger. El se manifesta si pentru purtatorii liberi din banda de valenta. Pentru a descrie aceste pierderi se introduce coeficientul de absorbtie pe purtatori liberi . Cum in material exista un numar mare de purtatori liberi, necesari pentru a asigura degenerarea nu este neglijabil, ordinul lui de marime fiind de . Astfel se defineste coeficientul net de amplificare al mediului si conditia de emisie stimulata se scrie . Daca aceasta conditie este realizata, mediul poate amplifica radiatia cu frecventa . Cei "cativa fotoni" aparuti prin emisie spontana in vecinatatea jonctiunii vor fii amplificati prin procesul de emisie stimulata. Atingerea pragului emisiei stimulate se traduce printr-o crestere abrupta a semnalului luminos emis de dioda si printr-o directivitate crescuta a acestuia. Se spune ca in acel moment dioda este superradianta.

Electroabsorbtia in gropi cuantice

Se considera initial structura nepolarizata electric. In acest caz functia modulatoare pentru un electron din banda de conductie verifica ecuatia lui Schrdinger

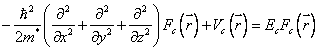, unde reprezinta potentialul de confinare in groapa unidimensionala, numeste functie modulatoare (infasuratoare) si este solutie a ecuatiei si se considera de forma . Astfel se obtine valoarea energiei la marginea inferioara a subbenzi : , unde reprezinta marginea inferioara a benzii de conductie, iar energia radiatiei absorbite se poate scrie cu masa redusa a perechii electron- gol. Folosind formula densitatii de stari in cazul 2D se poate determina coeficientul de absorbtie , deci inaltimea fiecarei trepte este proportionala cu integrala de suprapunere . Daca perpendicular pe straturile semiconductoare se aplica un camp electric, in expresia hamiltonianului intervine si expresia campului electric. Astfel se observa o deplasare a nivelelor energetice in camp electric, asa incat este mai mic pentru . Golurile si electronii sunt deplasati in sensuri opuse de catre campul electric, probabilitatea de localizare este maxima in vecinatatea lui pentru electron respectiv , unde L este lungimea gropii de potential. De asemenea functiile de unda (cel putin pentru nivelele inferioare) nu mai sunt ortogonale pentru . Prin urmare, multe dintre tranzitiile interzise in absenta campului (cand exista regula de selectie ) devin acum permise (in special in gropile cu lungime mare).

IV.    Tipuri de laseri

1. Laserii cu structuri mezoscopice

Din punct tehnologic, laserii cu gropi cuantice sunt mai usor de obtinut, si din acest motiv mult mai utilizati decat cei cu fire respectiv puncte cuantice.

Laserii cu gropi cuantice pot avea una sau mai multe gropi in mediul activ. In primul caz se numesc SQW (single quantum well) in al doilea caz MQW ( multiple quantum well). In ambele cazuri regina activa este separata printr-un start intermediar SCH (separate confinement heterostructure) de regiunile dopate sau , care reprezinta sursa de purtatori. Aceste regiuni au rolul de a creste gradul de confinare (localizare) a radiatiei emise in regiunea activa, actionand ca un ghid de unda pentru radiatia optica.

Structurile mezoscopice (in particular gropile cuantice) sunt nedopate, pentru ca nivelele energetice sa ramana discrete.

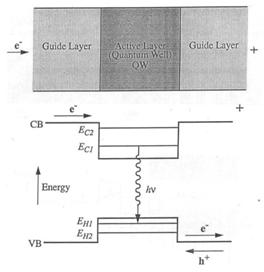
Fig 4.1 Schema de principiu a laserului cu groapa cuantica

Laserii cu gropi cuantice multiple

Laserii cu gropi cuantice multiple sunt realizati din 2 staturi alternative diferite de semiconductori, de exemplu care formeaza o heterostructura cuantica. Straturile sunt crescute folosind epitaxia moleculara sau depunere cu vapori. Unda emisa este determinata de grosimea straturilor dar si de materialele utilizate. Acesta este principalul avantaj fata de diodele laser, a carui lungime de unda depinde de banda interzisa a materialului.

Lungimea de unda a laserelor este cuprinsa intre , acoperind astfel infrarosul mediu.

Straturile alternative determina variatia potentialului pe toata lungimea materialului, astfel se variaza si probabilitatea de ocupare de catre electron a diferitelor stari. Prin alegerea cu grija a materialelor din compozitia laserului si cu un camp electric aplicat structurii, subbanda energetica minima a unui strat poate fi adusa la acelasi nivel cu energia minima a subbenzi superioare a stratului urmator.

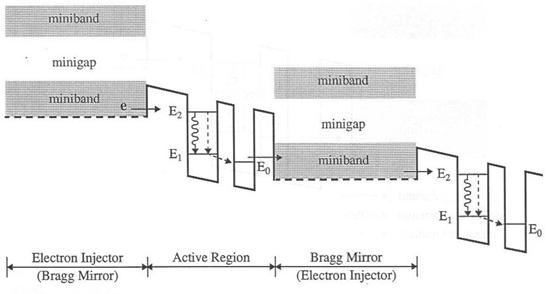
Fig 4.2 Schema de principiu a unui laser in cascada

Astfel un electron poate participa la o tranzitie optica intre benzile unui strat inainte de a tunela in structura urmatoare. Acest proces se poate repeta de mai multe ori, in functie de numarul de straturi, crescand astfel puterea optica de iesire.

Puterea de iesire mare, probabilitatea de tunelare ridicata si functionarea la temperatura camerei permit folosirea acestui tip de laser la masurarea variatiei atmosferei, inregistrandu-se concentratiile de gaze si poluanti (ca de ex. sau ) dar si pe post de radar, in conditii de vizibilitate scazuta. Independenta functionarii acestui tip de laser fata de valorile benzilor de valenta si conductie ofera o flexibilitate ridicata fata de un laser cu semiconductor (de ex. GaAs/AlGaAs)

V.       Fire cuantice semiconductoare

Calculele facute sunt realizate in unitati atomice, si anume pentru distante unitatea de masura este angstrom- ul , sau mai bine zis raza Bohr efectiva , pentru energie, unitatea de masura este dublul Rydgberg efectiv. Trecerea de la valoarea de dublul Rydgberg efectiv la o a alta unitate atomica a energiilor se face: . In cazul de fata s-a considerat o raza a firului cuantic de , raza efectiva determinata in urma primului program fiind de , in cazul electronului respectiv de in cazul golului. S-a considerat ca golul fiind de tipul gol greu, pentru o comportare mai buna in camp magnetic. Campurile considerate sunt campuri mari, cuprinse intre 0 si 15 de Tesla.

In rezolvarea programelor s-au ales functii de unda de tip hipergeometrice: 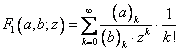sau solutii ale functiilor Bessel: ( BesselJ) sau (BesselK). Raza efectiva a fost introdusa deoarece aceste functii sunt determinate in cazul unei bariere de potential infinite (si nu finite cum este real), asa ca pentru a compensa bariera de energie finite fata e cea teoretica infinita fost folosita o raza efectiva in locul razei reale a firului cuantic.

Ecuatia Schrdinger, cu functii si valori proprii atemporala , unde expresia hamiltonianului este de forma:

, reprezinta energia potentiala in camp magnetic . Simetria problemei impune trecerea la coordonate cilindrice. In acest caz, hamiltanoianul se scrie:

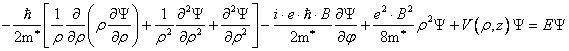
Astfel primul program se refera la calculul razei efective, in cazul campului extern , , 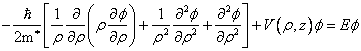solutia generala este de forma: , o functie plana pe directia Oz, semn ca electronul se misca liber pe aceasta directie, functie ce depinde de numarul cuantic magnetic si o functie necunoscuta . In starea fundamentala, , se poate scrie ca fiind:

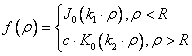, unde

este functia Bessel de ordinul intai, este functia Bessel de ordinul al doilea,

si .

Din conditia de continuitate in , se determina energia. Odata aflata energia, se determina raza efectiva, din conditia anularii functiei Bessel.

Cel de-al doilea program permite determinarea energiei in camp magnetic. In acest caz, starea fundamentala ecuatia functiei de unda este verificata de:

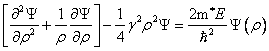, unde in unitati atomice. Folosind schimbarea de variabila , , cu . Solutia cautata este de forma , asta inseamna , solutia fiind satisfacuta de seria hipergeometrica degenerata . Insa se poate calcula efectul campului magnetic asupra electronului folosind o metoda variationala. Fie o functie de patrat integrabil si se calculeaza , cu . Se stie ca functiile proprii ale operatorului hamilton formeaza o baza , astfel incat se respecta regula de ortonormare a functiei, adica , iar .

In urma calculelor, se obtin o serie de valori ale energiei, valoarea apropiata de valoarea corecta fiind primul minim intalnit (parametru ).

Tabel 5.1 - contine valoarea energiei pentru campuri cuprinse intre 0 si 15 T, valori obtinute cu metoda razei efective si metoda variationala

Similar cu primele doua programe se procedeaza si in cazul golurilor. Se determina urmatoarele valori:

Tabel 5.2 contine valoarea energiei golului pentru campuri cuprinse intre 0 si 15 T

Astfel se poate determina valoarea potentialului in care se afla atat electronul cat si golul. O structura de tipul cu este un semiconductor cu gap direct (in cazul de fata ).

De asemenea

Astfel iar .

   

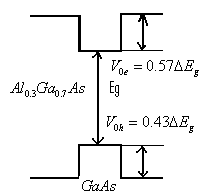
Fig 5.1 Stratul de actioneaza ca o bariera de potential

Tabel 5.3-contine valoarea energiei benzii interzise a heterostructurii pentru campuri cuprinse intre 0 si 15T

De asemenea se poate reprezenta si grafic probabilitatile de localizare a particulelor. De asemenea se observa ca, ca si in cazul electronilor, energia golurilor-grele creste odata cu marirea campului magnetic. Odata cu cresterea campului, valoarea benzii interzise creste, fapt ce a putut realizarea unor dispozitive cu banda interzisa modulata prin variatia campului magnetic.

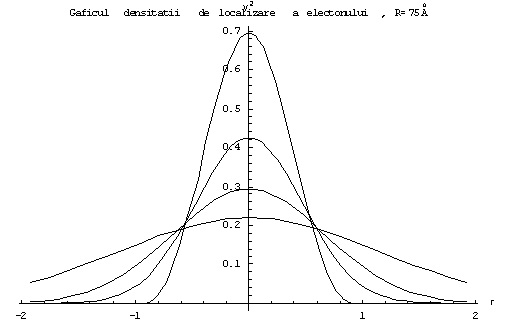
Fig 5.2 Graficul densitatii de localizare a electronului folosind metoda razei efective, pentru B= [0, 2.5, 7.5, 15] T. Odata cu cresterea campului are loc si o crestere a densitatii de localizare a particulei in centrul gropii de potential

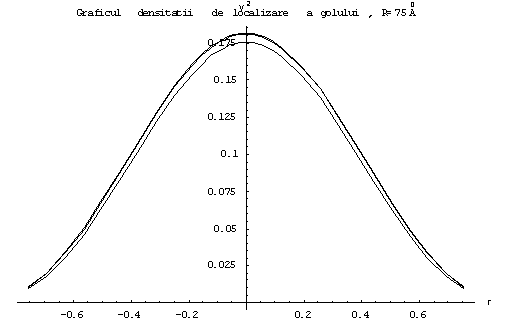
Fig 5.3 Graficul densitatii de localizare a electronului folosind metoda variationala, pentru B=[2.5, 7.5, 15]T

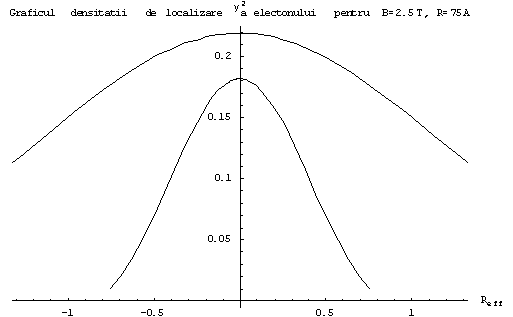
Fig 5.4 Graficul comparativ al densitatii de localizare a electronului pentru B=2.5T, folosind ambele metode. Functia de unda in cazul metodei variationale prezinta o comportare mai buna fata de metoda razei efective (functia de unda prezinta valori semnificative numai in centrul gropii).

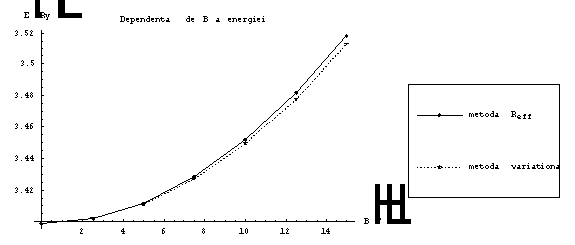
Fig 5.5 Dependenta de B a energiei electronului

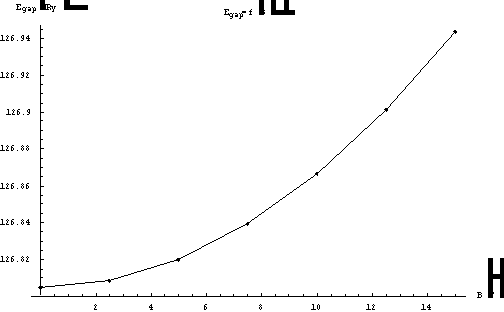
Fig 5.6 Graficul in functie de B

VI. Concluzii

In 1963 H. Kroemer din S.U.A. si Kazrinov si Alferov din fosta U.R.S.S. au sugerat primul laser cu gropi cuantice. In 1974 a fost facut primul laser cu gropi cuantice de catre J.P. Van der Ziel, R. Dingle, R.C. Miller, W. Wiegmann si W.R. Nordland, Jr. iar in 1994 a fost elaborat primul laser cu cascada.

Cercetatorii din California au reusit sa faca asa numitele "straturi de fire cuantice", folosind epitaxia de fasciculul molecular pentru a face straturi verticale. sau orizontale alternative de GaAs si straturi de conductivitate mai scazuta (AlGaAs)

Spre deosebire de semiconductorii uzuali, bazati pe siliciu, "firele cuantice" pot transforma energia de schimb a electronilor in lumina. Un electron excitat se poate relaxa, prin recombinare cu purtatorul pozitiv in stratul de GaAs, ei emitand lumina cu o lungime de unda specifica. Utilizand un laser, cu ajutorul caruia pompau energie, sub forma uni fascicul de mai multe frecvente, energie corespunzatoare unui dispozitiv simplu de "fir cuantic", ei au studiat energia de relaxare a electronului, pe un nivel energetic inferior. Experienta a verificat calculele facute, si anume lumina emisa de doua straturi diferite era diferita.

Aceste calcule au fost facute la laboratoarele AT&T Bell din Murray Hill si la institutul Bell Core din Red Bank, New Jersey de catre James P. Harbison, Leonard C. Feldman, F. Petroff

Bibliografie:- P. Sterian- Fotonica

Shallow Donors in a Quantum Well Wire: Electric Field and

Geometrical Effects

-https://www.mtmi.vu.lt/pfk/funkc_dariniai/nanostructures/

quant_structures.htm

-Donald A. Neamen Semiconductor Physics and Devices

-https://edu.ioffe.ru/links/pub/?ref=110

-Computational Optoelectronics of Semiconductor

Nanostructures Including Many-Body Effects Torsten Meier,

Huynh Thanh Duc, Matthias Reichelt, Bernhard Pasenow,

Tineke Stroucken and Stephan W. Koch

https://www.lasalle.edu/academ/chem/laser_web