Largimea regiunii de trecere la echilibru termic

Largimea regiunii de trecere la echilibru termic

Pentru descrierea matematica exacta a fenomenelor din jonctiunea pn se utilizeaza ecuatia lui Poisson:

(12.22)

unde r_v = Q/V (V fiind volumul jonctiunii pn) se numeste densitatea volumica de sarcina si e este permitivitatea electrica a mediului.

Pentru determinarea largimii regiunii de trecere a unei jonctiuni pn abrupte, se utilizeaza un model unidimensional simplificat (de-a lungul axei Ox) numit modelul Schottky (Fig. 12.6 a). Acest model are la baza aproximatia de golire, conform careia, jonctiunea pn se imparte in trei regiuni: regiunea de trecere situata in jurul jonctiunii metalurgice care este cuprinsa intre si doua regiuni neutre, una situata in semiconductorul de tip p, cuprinsa intre iar cealalta in semiconductorul de tip n si cuprinsa intre . Toate fenomenele specifice jonctiunii pn la echilibru termic se petrec in regiunea de sarcina spatiala. Aproximatia de golire considera ca in regiunea de sarcina spatiala sarcina concentratiile de electroni si goluri se neglijeaza fata de concentratiile de impuritati, adica regiunea de trecere este complet saracita in purtatori mobili de sarcina, singura sarcina fiind sarcina spatiala Q_p si Q_n data de ionii negativi si respectiv pozitivi de impuritati.

Fig. 12.6. Modelul Schottky unidimensional al jonctiunii pn: a) jonctiunea pn, b) densitatea volumica de sarcina r_v, c) variatia campului electric intern , d) variatia potentialului electric U(x).

Avand in vedere relatiile (12.3) si (12.4) ale sarcinilor spatiale, densitatile volumice de sarcina r_v (Fig. 12.6 b), in cele doua regiuni sunt date de relatiile:

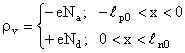(12.23)

Distributiile campului electric si a potentialului electric se pot deduce din rezolvarea ecuatiei Poisson in cazul unidimensional:

(12.24)

cu conditiile la limita:

(12.25)

pentru campul electric la echilibru termic si:

(12.26)

pentru potentialul electric.

In regiunile neutre si , campul electric este nul, iar potentialul este constant.

Pentru regiunea de trecere din semiconductorul de tip p:, unde , din ecuatia lui Poisson se obtine:

(12.27)

sau daca se tine seama de legatura dintre campul electric si potential:

(12.28)

se obtine:

(12.29)

Integrand relatia (12.29) intre () si x< , rezulta:

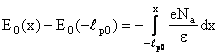(12.30)

sau daca se are in vedere conditia la limita pentru campul electric , se obtine distributia campului electric In aceasta regiune:

(12.31)

Integrand apoi relatia (12.28) se obtine distributia potentialului electric:

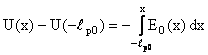(12.32)

sau daca se tine seama de conditia la limita a potentialului (12.26), , rezulta:

(12.33)

Analog pentru regiunea de trecere din semiconductorul de tip n, unde , pentru campul electric se obtine:

(12.34)

care prin integrare si impunerea conditiei la limita , devine:

(12.35)

Pentru potentialul electric in aceasta regiune rezulta:

(12.36)

Tinand seama de conditia la limita (12.26): la potentialul electric este , din relatia (12.32) rezulta:

Mai departe, impunand conditia de continuitate a intensitatii campului electric la x = 0, din relatiile (12.38) si (12.39) se obtine:

(12.38)

relatie care exprima neutralitatea globala a semiconductorului la echilibru termic.

Relatia (12.38) indica faptul ca regiunea de sarcina spatiala patrunde mai puternic in regiunea mai slab dopata a jonctiunii pn.

Largimea totala a regiunii de trecere: se poate calcula daca se tine seama de conditia de continuitate a potentialului la x=0 (Fig. 12.6 d), din care se obtine:

Din relatiile (12.34) si (12.35) se obtine largimea regiunii de trecere la echilibru termic:

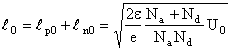(12.40)

Relatia (12.40) arata ca largimea totala a regiunii de trecere depinde numai de concentratiile de impuritati si mai ales de concentratia impuritatilor din regiunea mai slab dopata si de tensiunea interna U₀. In acest caz largimea totala a regiunii de trecere se gaseste numai in regiunea mai slab dopata.

De exemplu, pentru o jonctiune asimetrica de forma n⁺p pentru care N_d>>N_a, largimea regiunii de trecere are expresia aproximativa:

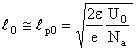(12.41)

iar pentru o jonctiune asimetrica de forma p⁺n pentru care N_a>>N_d, largimea regiunii de trecere va fi:

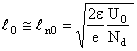(12.42)

Din relatiile (12.31) si (12.35) se observa ca intensitatea campului electric in regiunea de trecere este negativa in ambele regiunii p si n, avand o variatie liniara cu distanta (Fig. 12.6 c), atingand o valoare maxima, in modul, la x=0:

(12.43)

Exprimand largimea regiunii de trecere din regiunea p, sau din regiunea n, , in functie de largimea totala a regiunii de trecere se poate obtine valoarea maxima a campului electric.

Din relatiile (12.38) si (12.40), se gasesc largimile si :

si apoi din relatia (12.43), unde se tine seama de relatia (12.40), se obtin relatiile:

(12.46)

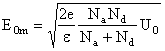(12.47)

Pentru jonctiuni asimetrice campul electric maxim depinde si se gaseste, ca si largimea totala a regiunii de trecere, numai in regiunea mai slab dopata. Pentru o jonctiune asimetrica de forma n⁺p, cu N_d>>N_a:

(12.48)

iar pentru jonctiune de tipul p⁺n, cu N_a>>N_d:

(12.49)