Studiul experimental al dependentei de temperatura a rezistentei electrice

Introducere

Scopul lucrarii este de a verifica experimental modul cu se modifica rezistenta electrica la metale si semiconductoare cand se modifica temperatura acestora. Dupa cum vom demonstra in cele ce urmeaza, variatia rezistentei electrice cu temperatura este efectul modificarii parametrului de material numit rezistivitate electrica (sau a conductivitatii electrice care este inversul rezistivitatii).

Teoria clasica a conductivitatii electrice: rezistenta, rezistivitate, conductivitate

In teoria clasica a fenomenului de conductie electrica este folosit modelul gazului de electroni. In acest model, electronii liberi (cazul unui conductor metalic) se comporta ca moleculele unui gaz avand o miscare dezordonata (prin ciocnire cu reteaua cristalina) cu viteza termica .

Fie un conductor metalic de lungime , sectiune , rezistenta electrica , supus la o diferenta de potential (determinata din exteriorul conductorului- sursa de tensiune electromotoare si restul circuitului de care apartine conductorul). Conform legii lui Ohm pentru o portiune de circuit, aceste marimi sunt legate cauzal sub forma

. (1)

Rezistenta electrica este o marime macroscopica care masoara inertia electrocinetica a portiunii de circuit (a conductorului definit mai sus) si depinde de lungimea si sectiunea conductorului, care sunt, din punct de vedere al electromagnetismului, parametrii sistemului nespecifici.

Trecerea, de la forma locala

sau (2)

( este conductivitatea electrica si este rezistivitatea electrica) la forma integrala (1), implica urmatoarea dependenta a rezistentei conductorului de rezistivitate

. (3)

Deoarece unitatea de masura a rezistentei, in SI, este ohmul, , unitatea de masura pentru rezistivitate este

. (4)

Legea locala este valabila, sub forma (2), pentru intensitati ale campului mai mici de un milion de volti pe metru. Aceasta valoare corespunde acelei intensitati care determina intre doua ciocniri o viteza de drift egala cu viteza medie in miscarea dezordonata (apropiata ca valoare de viteza termica). Abateri de la lege avem si in cazul cand campul este variabil in timp si variatiile periodice au o perioada mai mica decat timpul mediu intre doua ciocniri.

Variatia rezistivitati si a rezistentei cu temperatura

Rezistivitatea este un parametru de material microscopic care depinde de temperatura materialului. Rezistivitatea masoara inertia electrocinetica ca rezultat al interactiunii purtatorilor intre ei si cu reteaua cristalina. Aceasta interactiune se opune miscarii ordonate a purtatorilor.

Conform teoriei clasice a conductiei electrice, pentru metale (numarul de purtatori este independent de temperatura, rezistivitatea depinde de temperatura, prin intermediul vitezei termice

(5)

si deci este proportionala cu temperatura absoluta la puterea ( si se neglijeaza faptul ca si drumul liber mediu depinde de temperatura). Experimental, pentru metale, se constata ca rezistivitatea depinde liniar

. (6a)

In expresia (6a), este rezistivitatea la temperatura de si este un coeficient apropiat ca valoare de . Din acest motiv, relatia dependenta rezistivitatii metalelor de temperatura absoluta () este

. (6b)

Dependenta liniara este valabila la variatii ale temperaturii , in jurul valorii de zero grade Celsius, de ordinul zecilor de grade. Pentru variatii mai mari, apare un efect neliniar, prin termeni proportionali cu puterea a doua a temperaturii, de forma .

La semiconductori, dependenta de temperatura a rezistivitatii este determinata de cresterea numarului de purtatori cu cresterea temperaturii (si nu de procesul de interactiune cu reteaua). Deoarece numarul de purtatori creste exponential cu cresterea temperaturii, rezistivitate scade exponential cu cresterea temperaturii

(7a)

Subliniem faptul ca relatiile (6) si (7) nu sunt valabile la temperaturi apropiate de zero kelvini cand apare fenomenul de supraconductibilitate.

O categorie interesanta de materiale, din punct de vedere al aplicatiilor, a caror rezistivitate scade cu cresterea temperaturii sunt oxizii metalelor de tranzitie (Fe, Mn, Zn). Dispozitivele construite din aceste materiale se numesc termistoare. Legea de variatie este tot exponentiala dar se exprima in functie de rezistenta la o temperatura de referinta (de obicei temperatura care poate fi considerata ca fiind temperatura camerei)

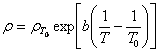(7b)

Daca neglijam fenomenul de dilatare termica a conductorului (modificarea lungimii si sectiunii), conform relatiei     (3), dependenta rezistentei de temperatura este ca si cea a rezistivitatii:

, (8)

pentru conductorii metalici si

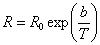, (9a)

sau

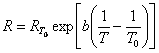(9b)

pentru semiconductori.

Diferenta dintre rezultatele teoretice si cele experimentale pun in evidenta faptul ca modelul clasic al dependentei de temperatura nu este corect. Dependenta corecta a rezistivitatii de temperatura este obtinuta in teoria cuantica a conductiei electrice.

Supraconductibilitatea

Unele substante, racite la temperaturi sub o anumita valoare, isi modifica rezistivitatea care poate sa ajunga la zero, conductivitatea electrica devenind infinita. Acest fenomen se numeste supraconductibilitate. Materialele respective se numesc materiale supraconductoare . Fenomenul a fost observat prima data in anul 1911 de catre H. Kamerling Onnes pentru mercur (4,15 K), staniu (3,8 K) si plumb (7,2 K). Teoria care explica supraconductibilitatea a fost fundamentata in anul 1957 de: J. Bardeen, L. N. Cooper si J. B. Schrieffer, este cunoscuta ca teoria BCS si este o teorie cuantica. Cei trei autori explica fenomenul prin faptul ca electronii, care sunt fermioni si nu pot exista decat cate unul in fiecare stare (principiul lui Pauli) formeaza perechi care au spinul zero si din acest motiv se comporta ca bozonii care pot fi mai multi in aceeasi stare (in cazul nostru, starea de miscare ordonata). Formarea perechilor este posibila, la temperaturi mici, cand miscarea haotica a electronilor devine atat de slaba incat fortele de atractie magnetica dintre electroni mentine perechea formata. Perechile de electroni nu se mai ciocnesc cu reteaua si deci efectul termic inceteaza si implicit rezistivitatea materialului se anuleaza. Pana in deceniul al 9-lea al secolului douazeci, supraconductibilitate se obtinea greu deoarece erau necesare instalatii costisitoare de racire la temperaturi apropiat de zero kelvin. Ulterior, au fost obtinute materiale care devin supraconductoare la temperaturi mai mari, de ordinul 100-150K. Cercetarile in acest domeniu sunt importante deoarece, obtinerea supraconductibilitatii la temperaturi de ordinul a 300K ar produce o revolutie in electrotehnica si electronica (reduce pierderile in retelele de transport, se obtin campuri magnetice mai intense, nu mai sunt necesare sistemele de racire a instalatiilor electrice si electronice etc.).

Montajul experimental

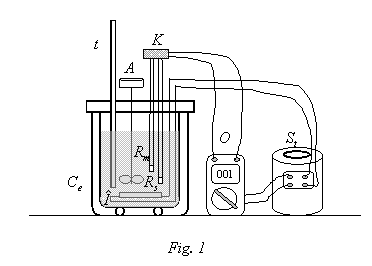
Montajul experimental este alcatuit din: calorimetru electric prevazut cu termometru , rezistenta metalica , rezistenta semiconductoare , ohmetru digital conectat printr-un comutator la cele doua rezistente si sursa de alimentare (transformator) pentru incalzitor si ohmetru. Rezistentele sunt incalzite prin intermediul uleiului din calorimetru. Uniformizarea temperaturii in baia de ulei a calorimetrului se face cu ajutorul uni agitator cu palete.

Se masoara temperatura uleiului din calorimetru care, in cazul cand este uniforma in tot volumul, este si temperatura celor doua rezistente. Apoi, cu ajutorul comutatorului se cupleaza pe rand cele doua rezistente la ohmetru. Se noteaza datele in tabel.

Cu ajutorul datelor din tabel se traseaza curbele si , tinand cont de erorile de citire ale temperaturii si rezistentelor. Pentru rezistenta metalica se poate calcula coeficientul , conform relatiei

, (10)

Erorile pentru coeficientul se determina conform relatiilor:

, (11)

. (12)

Cu ajutorul reprezentarii grafice se poate afla valoarea rezistentei metalice la temperatura de zero grade Celsius si temperatura la care rezistenta ar trebui sa devina zero (teoretic ). Practic s-a observat ca rezistenta se anuleaza la temperaturi superioare punctului de zero absolut (). In cazul rezistentei semiconductoare se observa scaderea acesteia dupa o curba exponentiala.