UNDE ELECTROMAGNETICE - CAMP ELECTROMAGNETIC

UNDE ELECTROMAGNETICE

CAMP ELECTROMAGNETIC

Campul electromagnetic, se caracterizeaza, din punct de vedere macroscopic: printr-o distributie si evolutie continua in timp si spatiu, cu un impuls, un moment cinetic, o energie (de natura electromagnetica) prin intermediul caruia se transmit din punct in punct, cu o viteza finita (nu poate depasi viteza luminii in spatiul liber) actiuni de tip electromagnetic.

Campul electromagnetic este constituit din doua componente: campul electric, definit de vectorul intensitate camp electric si campul magnetic, definit de vectorul camp magnetic , vectori ce depind de coordonatele de pozitie ale unui punct din spatiu si de timp (precizam ca in sistemul de unitati S.I. unitatea de masura pentru campul electric este; volt/metru, iar unitatea de masura pentru campul magnetic este: tesla = 10⁴ gauss; atragem atentia asupra faptului ca vectorul inductie magnetica). Cele doua componente ale campului electromagnetic se afla intr-o stransa interdependenta: un curent electric de conductie (sau de convectie) si un camp electric variabil in timp dau nastere la un rotational al campului magnetic,dupa cum un camp magnetic variabil in timp da nastere la un rotational al campului electric, de semn schimbat. Aceasta interdependenta isi gaseste confirmarea in teoria clasica a campului electromagnetic, elaborata de J.C. Maxwell (1864) si care abordeaza studiul fenomenelor electromagnetice din punct de vedere fenomenologic (acest studiu este raportat la nivelul macroscopic de organizare al materiei).

Extinderea teoriei clasice a campului electromagnetic la electroni (particule elementare cu sarcina electrica negativa, cu o masa de repaus bine

determinata, care intra in structura fiecarui atom) l-a condus pe H. Lorentz la elaborarea teoriei clasica electronilor, cunoscuta si sub numele de teoria clasica a campului electromagnetic microscopic (1895) (atragem atentia asupra faptului ca in cadrul acestei teorii nu se iau in considerare efectele cuantice si utilizarea notiunii "microscopic" trebuie privita doar in sensul ca teoria respectiva se bazeaza pe existenta electronilor, care genereaza asa-numitul camp electromagnetic microscopic).

Elaborarea electrodinamicii corpurilor in miscare (studiul fenomenelor electromagnetice pentru corpuri in miscare) de catre H. Hertz si H. Lorentz, prin generalizarea ecuatiilor Maxwell-Lorentz pentru medii materiale in miscare, precum si diversele experiente de natura fizica efectuate in cadrul electrodinamicii corpurilor in miscare, au constituit fundamentale pe care sa bazat elaborarea teoriei relativitatii restranse de catre A. Einstein (1905). Studiul fenomenelor electromagnetice prin prisma teoriei relativitatii restranse a pus intr-o noua lumina notiunea de camp electromagnetic, unitatea dintre campul electric si campul magnetic primind o semnificatie fizica mult mai profundam in cadrul acestei teorii.

Un pas deosebit de important pe calea dezvoltarea teoriei campului electromagnetic l-a constituit cuantificarea campului electromagnetic, care face parte integranta dintr-o ramura a electrodinamicii, cu importante implicatii teoretice si aplicative, cunoscuta sub numele de electrodinamica cuantica (dintre problemele centrale cu care se ocupa electrodinamica cuantica sunt: campul fotonic, interactiunile dintre electroni si fotoni s.a.). Generalizarea acestor rezultate pentru cuantificarea campurilor asociate si altor particule "elementare" (nucleoni, mezoni s.a.) constituie obiectul de studiu al teoriei cuantice a campurilor, disciplina cu importante aplicatii in diverse domenii ale fizicii: fizica particulelor "elementare", fizica tranzitiilor de faza s.a.(aceste probleme, cat si altele, vor fi analizate in detaliu la disciplinele respective).

2.UNDE ELECTROMAGNETICE

2. Ecuatiile de propagare a undelor electromagnetice in medii materiale

Este binecunoscut faptul ca o distributie spatiala de sarcini electrice variabila in timp , respectiv curentii electrici variabili in timp, , creeaza in spatiul inconjurator un camp electromagnetic variabil (in spatiu si in timp), care se va propaga sub forma de unde electromagnetice. Viteza de faza v a acestora unde este: fie mai mica decat viteza c luminii in spatiul liber (vid), (daca undele se propaga in medii materiale), fie egala cu viteza c a luminii in spatiul liber (daca undele electromagnetice se propaga in acest spatiu).

Teoretic, existenta undelor electromagnetice a fost prevazuta, pentru prima oara de catre Faraday si apoi de catre Maxwell,iar experimental au fost puse in evidenta de catre Hertz (1888).

In prezent se cunoaste un spectru foarte larg de unde electromagnetice, cu diverse proprietati fizice si cu numeroase aplicatii in: radiocomunitatii, electronica, optica cuantica, spectroscopie, precum si in alte domenii ale fizicii.

2. Ecuatiile de propagare a undelor electromagnetice in semiconductoare

Este important sa precizam de la inceput care este criteriul dupa care putem defini un mediu material, din punct de vedere electromagnetic, in ceec ce priveste fenomenul de propagare a undelor electromagnetice in mediile respective. Acest criteriu este dat de raportul dintre marimea densitatii curentului de conductie si marimea densitatii curentului de deplasare electrica, deoarece prin acest raport obtinem valoarea conductivitatii electrice a mediului fata de valoarea permitivitatii mediului respectiv. Dupa cum se stie de la ecuatia Maxwell-Ampre, unde este vectorul densitate de curent de conductie, iar este vectorul densitate de curent de deplasare electrica. Daca admitem ca intensitatea campului electric variaza periodic cu timpul: , unde are semnificatia unei amplitudini, rezulta

(1)

Facand raportul dintre marimile si .

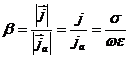(2)

distingem trei cazuri:

1. pentru, marimea densitatii curentului de conductie este de acelasi ordin de marime cu cea a densitatii curentului de deplasare (cazul semiconductoarelor);
2. pentru, , predomina densitatea curentului de conductie fata de densitatea curentului de deplasare (cazul metalelor);
3. pentru,, predomina densitatea curentului de deplasare fata de densitatea curentului de conductie [cazul    dielectricilor (al izolatoarelor)].

Asadar, ne situam in conditia prezentata la cazul Pentru a obtine ecuatia de propagare a undelor electromagnetice intr-un astfel de mediu, procedam astfel: aplicam operatorul "rotational" ecuatiei si tinem seama de ecuatia din sistemul de ecuatii Maxwell. Obtinem egalitatea:

(3)

unde am pus (4) si am tinut seama ca: (5). Daca avem in vedere relatia vectoriala: (6) (deoarece ), egalitatea (3) capata forma:

(7)

Inlocuind ecuatia in (7) obtinem

(8)

Aceasta este ecuatia de propagare a campului magnetic in mediul considerat.

Pentru a obtine ecuatia de propagare a campului electric , procedam in mod analog, cu deosebirea ca aplicam operatorul rotational ecuatiei (9), apoi tinem seama de ecuatia si de ecuatia unde luam (admitem nu ca in mediu nu exista sarcini electrice libere). Se obtine ecuatia

(10)

Aceasta este ecuatia de propagare a campului electric in mediul considerat.

2.2. Ecuatiile de propagare a undelor electromagnetice in conductoare

Propagarea undelor electromagnetice intr-un mediu conductor se studiaza luand in considerare conditia de la cazul 2 (analizat la pct. 2.2.1). Ecuatia de propagare a undelor electromagnetice in conductori (metale) se obtine printr-un procedeu analog cu cel utilizat la pct. 2. cu precizare ca in ecuatia neglijam curentul de deplasare electrica fata de curentul de conductie. Facand calculele, obtinem ecuatiile de propagare a campului magnetic si a campului electric in conductor:

(12)

2.3. Ecuatiile de propagare a undelor electromagnetice in dielectrici

Propagarea undelor electomagnetice intr-un mediu dielectric se studiaza luand in considerare criteriul de la cazul 3 (analizat la pct. 2.2.1). Obtinerea ecuatiilor de propagare a campului magnetic si a campului electric intr-un mediu conductor se face printr-un procedeu analog cu cel utilizat la pct. 2.2.1 cu precizarea ca in ecuatia se neglijeaza curentul de conductie fata de curentul de deplasare. Ecuatiile respective sunt de forma

(13)

si

(14)

unde

v este viteza de faza a undelor electromagnetice in mediul dielectric

3. ECUATIILE DE PROPAGARE A POTENTIALELOR ELECTROMAGNETICE

3. Ecuatiile de propagare a potentialelor in prezenta distributiei de sarcini electrice si a curentilor electrici

Pentru a stabili ecuatiile de propagare a potentialelor electrodinamice si intr-un mediu in care exista o distributie spatiala de sarcini electrice libere si o densitate de curent de conductie si o densitate de curent de deplasare , utilizam ecuatiile lui Maxwell (16) si (17) , unde inlocuim campul magnetic prin relatia (18), iar campul electric prin relatia (19). Obtinem egalitatile

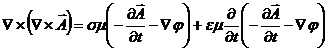(20)

si

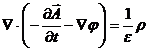(21)

Daca avem in vedere relatia vectoriala: (22)si egalitatea operatoriala: (23), ecuatiile (20) si (21) capata forma

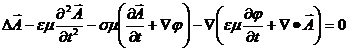(24)

Si

(25)

Sa observam un fapt important: ne putem alege astfel potentialul vector , in functie de potetialulscalar φ, incat sa avem verificata conditia

(26)

Aceasta este asa-numita conditie a lui Lorentz.

Inlocuind (26) in ecuatia (24), aceasta capata forma

. (27)

Deoarece din ecuatia (26), rezulta

(28)

ecuatia (25) se poate scrie si sub forma

(29)

Aceasta este ecuatia de propagare a potentialului scalar , care este o ecuatie diferentiala de ordinul doi neomogena, cu derivate partiale.

Ecuatia de propagare a potentialului vector obtinem din egalitatea (26), unde ultimii doi termeni ii trecem in partea dreapta a egalitatii respective, iar vectorul densitate de curent de conductie il scriem sub o alta forma:

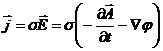(30)

Obtinem

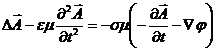(31)

Inlocuind (30) in (31) rezulta

Aceasta este ecuatia de propagare a potetialului vector si este de aceasi forma cu ecuatia diferetiala (29).

3.2. Ecuatiile de propagare a potentialelor in absenta distributiei de sarcini electrice si a curentilor electrici

In cazul in care mediul material se caracterizeaza prin absenta distributiei de sarcini electrice libere si a curentului electric de conductie , ecuatiile (29) si (30) se reduc la forma:

(33)

si

(34)

Ecuatiile respective sunt de forma ecuatiilor de propagare a undelor electromagnetice iin dielectrici.

Daca introducem operatorul lui d'Alambert

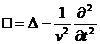(35)

Ecuatiile (33) si (34) capata forma

(36)

si

Sa observam ca in cazul in care propagarea undelor electromagnetice respectiv a potetialelor, se face in spatiul liber, se inlocuieste, in ecuatiile de propagare respective, viteza de faza cu viteza luminii , unde ε permitivitatea spatiului liber, μ este permeabilitatea spatiului liber.

4. PROPAGAREA UNDELOR ELECTROMAGNETICE IN DIELECTRICE

Sa analizam modul de propagare a undelor electromagnetice intr-un mediu dielectric. Ecuatiile de propagare utilizate sunt de forma si si pe care le putem scrie ca o singura ecuatie de propagare

(38)

daca prin vectorul intelegem fie vectorul , fie vectorul . Discutia solutiei ecuatiei diferentiale (38) o limitam la cazul undei plane. Aceasta se poate scrie sub forma

unde si sunt doua functii vectoriale arbitrare, periodice in spatiu si timp, iar este faza undei electromagnetice [ este vectorul de pozitie al unui punct situat pe planul de faza, a carei    ecuatie este este versorul normala la planul de faza, ν este frecventa undei, este vectorul de unda ( este lungimea de unda, este versorul vectorului de unda )]. Sa observam ca functia reprezinta unda electromagnetica progresiva, care se propaga in sensul pozitiv al vectorului , iar functia reprezinta unda electromagnetica regresiva, care se propaga in sensul negativ al vectorului .In problemele de propagare a undelor vom utiliza doar unda progresiva, astfel ca solutia (39) se poate scrie sub forma:

(40)

unde ; sunt cosinusii directori ai versorului . Functia se poate exprima: fie prin cosinus, fie prin sinus, al carui argument este tocmai faza . Deci

sau   

, (41)

unde amplitudinea undei (poate fi o marire complexa). De asemenea, putem scrie functia ca solutie a ecuatiei undelor, si sub forma exponentiala:

. (42)

Aceasta reprezinta o unda plana monocromatica (o unda a carei lungime de unda,respectiv frecventa, sunt bine determinate).

In concluzie, solutiile ecuatiilor de propagare si sunt undele electromagnetice plane monocratice, de forma:

(43)

si

,    (44)

unde este amplitudinea undei magnetice, iar este amplitudinea undei electrice (aceste amplitudini pot fi si marimi complexe).

Pentru a determina transversabilitatea undelor electromagnetice in medii dielectrice, scriem sistemul de ecuatii Maxwell in cazul unui mediu dielectric (unde se neglijeaza curentul de conductie, nu exista o distributie de sarcini electrice libere):

,

,

,

,

unde vom calcula operatorii si in functie de faza a undei electromagnetice. Pentru aceasta calculam derivatele functiei in functie de variabilele: x, y, z, t. Tinand seama de solutia (40), obtinem:

,

, (45)

,

si deci

, (46)

iar derivata functiei in raport cu timpul t este:

. (47)

Asadar, operatorii si au urmatoarea forma:

, (48)

,

.    (49)

Avand in vedere formulele (48) si (49), ecuatiile si capata forma:

,   

si

. (51)

Prin integrare obtinem:

,    (52)

,    (53)

unde am renotat ( este versorul normala la planul de faza al undei). Din (52) si (53) rezulta:

    (54)

si

(55)

unde Deoarece

(56)

Formulele (54) si (55) se scriu in forma finala;

,    (57)

. (58)

Asadar, vectorul camp electric este perpendicular pe planul format de vectorii si , iar vectorul camp magnetic este perpendicular pe planul format de vectorii si .

Marirea acestor vectori este:

    (59)

    (60)

deoarece unghiul dintre vectorii este si deci sin .

Sa aratam ca vectorul perpendicular pe directia versorului si, de asemenea, si vectorul este perpendicular pe directia acestui vector. Pentru aceasta, inmultim scalar egalitatile (52) si (53) cu versorul :

,    (61)

    (62)

Tinand cont de regula produsului mixt, cele doua egalitati devin:

(63)

    (64)

deoarece Rezulta deci:

(65)

Aceasta ne dau conditia de perpendicularitate dintre vectorii respectivi.

In concluzie, vectorii si formeaza un triedru drept si undele electromagnetice se propaga in dielectrici sub forma de unde transversale. In teoria propagarii undelor electromagnetice o marime fizica importanta este impedanta Z a undei. Aceasta se defineste prin raportul:

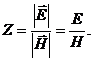    (66)

Aceasta ne arata ca impedanta undelor electromagnetice in dielectrici este o marime constanta. Vom calcula urmatoarele marimi: marimea P a vectorului Poynting densitatea de energie electromagnetica , marimea a vectorului densitate de impuls electromagnetic . Tinand cont de formulele (59) si (60), obtinem urmatoarele valori pentru marimile P si :

,    (68)

(69)

.    (70)