CAMP ELECTROMAGNETIC VARIABIL - LEGILE CAMPULUI ELECTROMAGNETIC

CAMP ELECTROMAGNETIC VARIABIL

1. LEGILE CAMPULUI ELECTROMAGNETIC

In teoria macroscopica-fenomenologica, campul electromagnetic i se asociaza mai multe marimi de stare : -intensitatea campului electric; -intesitatea campului magnetic; -inductia electrica; -inductia magntica. Intre aceste marimi exista relatiile exprimate prin ecuatiile Maxwell-Minkowski, care sub forma globala se scriu:

(1)

(2)

(3)

(4)

unde C este o curba inchisa , F o suprafata deschisa ce se sprijina pe C, C=FrF, G este o suprafata inchisa, iar este versorul dupa normala la suprafata considerata. In ecuatia (1) I este curentul electric care trece prin suprafata F, iar in relatia (3) Q este sarcina totala aflata in interiorul suprafatei G. Curentul total I este format din mai multi termeni:

Unde este densitatea volumica de curent electric de conductie, densitatea de suprafata de curent electric de conductie, iar un curent de linie. Prin C_i s-au notat curbele de intersectie dintre panzele de curent si suprafata F; I_c este curentul de convectie, iar I_i curentul imprimat. La mediile in miscare se pune in evidenta si curentul Roentgen de densitate, , unde este viteza locala a mediului.

FORMA LOCALA A ECUATIILOR LUI MAXWELL

Plecand de la legile globale, se poate stabili expresia diferentiala a acestor legi, utilizand relatia analizei vectoriale. Tinand seama de identitatile

,

si admitand ca, in jurul punctului considerat, I se reduce la un curent volumic, legea lui Maxwell se poate scrie:

,

de unde rezulta

. (5)

Aceasta relatie este o teorema care rezulta din legea globala (1).

Procedand in mod analog, se obtine:

(6)

In ceea ce priveste legile de stare, admitand ca Q provine numai din sarcini volumice, rezulta relatia:

(7)

Din ultima lege se obtine forma echivalenta:

(8)

Luand divergenta relatiei (1) si tinand seama de faptul ca , rezulta:

Permutand si si tinand cont de (3), rezulta ca a existat candva un moment in care si , se deduc ca teoremele legile de stare (3) si (4) din sistemul (1), (2) si (9).

In noul sistem de legi se pleaca de la relatiile locale (1), (2) si (9). luand divergenta primei relatii, rezulta, comutand operatorii si

(10)

Dar, conform cu (9), relatia (10) devine:

sau , unde c este o constanta in raport cu timpul.

Daca pentru exista un moment in care , atunci c=0 si rezulta legea lui Gauss: . In mod asemanator, plecand de la relatia (2), se deduce

Relatiile de continuitate se pot deduce si pentru curentii de suprafata si de linie.

3. FORMA ECUATIILOR CAMPULUI ELECTROMAGNETIC

Sub forma lui Maxwell, campul electromagnetic este descris prin ecuatii cu operatori care sunt liniare. Remarcam ca ecuatiile lui Maxwell sunt cele mai simple ecuatii vectoriale.

Astfel, cele mai simple relatii matematice prin care un camp scalar se ataseaza unui camp vectorial sunt:

In sistemul de unitati SI, luand , , , , regasim legea care asociaza intensitatea campului electric de potentialul scalar φ in cazul electrostatic. Luand , , si , regasim legea lui Gauss.

In mod asemanator se pot gasi legile de desfasurare din relatiile generala:

, unde D    este un operator diferential, in particular D =.

Aceste remarci ne permit a urmari eventualele modificari liniare ale ecuatiilor lui Maxwell, cautam conditiile pe care trebuie sa le satisfaca marimile a,b,c,d pentru ecuatiile

sa fie compatibile unele cu altele. Aplicand operatorul relatiei care corespunde legii inductiei, rezulta, tinand seama de modificarea legii polilor magnetici liberi:

.

La fel, din legile circuitului magnetic si a lui Gauss rezulta:

In medii fara sarcini si curenti aceste conditii devin:

Luand

;

prima relatie devine liniar relatia lui Lorentz si se gasesc modificarile liniare propuse de L. de Broglie pentru foton (b=0, c=0):

; ,

; ,

unde potentialele si φ satisfac relatiile clasice

;

.

4. CONDITIILE SATISFACUTE DE CAMP LA SUPRAFATA DE SEPARATIE A DOUA MEDII

Se pleaca de la legea lui Maxwell:

(11)

unde ψ este fluxul inductiei electrice prin F, iar I curentul care trece printr-o suprafata deschisa F, delimitata de curba inchisa C.

Pentru a determina relatia dintre valorile lui in celedoua medii, se ia conturul C un dreptunghi situat intr-un plan perpendicular pe supafata N de separatie a celor doua medii.

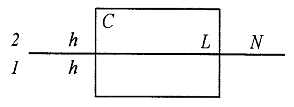
Fig.1.

Fie L intersectia dintre planul C si N. Daca din (11) deformand prin aplatizare pe C, rezulta cu :

,

unde k_t este componenta lui cuprinsa in N. Daca in punctul considerat k=0, atunci componenta tangentiala a lui trece in mod continuu prin suprafata de separatie a celor doua medii. Nu este insa obligatorie aceasta trecere continua, putand prezenta discontinuitati.

Daca una din componentele lui e nula si se reduce la , se poate scrie:

,

deorece este cumprins in planul normal la . Marimea permite deci explicarea unor discontinuitati in componenta tangentiala a lui . Pentru a justifica discontinuitatile campului electric, se introduce prin simterie marimea:

numita densitate de curent magnetic de suprafata. Semnul din fata parantezei se justifica ulterior.

Pentru discontinuitatile care apar in componentele normale ale campului electric, in mod firesc, plecand de la legea lui Gauss, se deduce:

unde G este o suprafata inchisa care cuprinde in ea sarcina totala Q

,

unde ρ este densitatea electrica de volum, η densitatea de sarcina de suprafata, w densitatea de sarcina in linie.

Suprafata G se ia un cilindru plat, avand bazele paralele cu N si care e sectionat de N.

Deformand pe G prin aplatizare astfel incat cele doua baze sa ramana de o parte si de alta a lui N, in cazul w=0 rezulta:

sau daca una din componentele e nula,

,

iar pentru mediile izotrope

.

Se explica astfel existenta unor discontinuitati in componenta normala a lui .

In mod simetric se introduce densitatea de suprafata de sarcina magnetica pentru a justifica discontinuitatile lui . Scriem :

.

Pentru mediile izotrope rezulta:

.

In modul acesta se arata ca pot aparea discontinuitati in unele componente ale campului electromagnetic.

La suprafata unui conductor perfect (σ=∞), campul electromagnetic are o structura deosebit de simpla. In interiorul conductorului este valabila legea lui Ohm, care, sub forma local, se scrie . Din conditia de stabilitate a sistemelor exprimata sub forma "intrare marginita iesire marginita", rezulta ca in conductor, pentru a avea , este necesar si suficient ca . Daca la suprafata conductorului perfect , componenta tangentiala a cimpului E trece in mod continuu, deci fiind nula in interiorul conductorului perfect, va fi nula si in corpul cu care acesta vine in contact. Rezulta deci ca, la suprafata unui conductor perfect, campul trebuie sa fie perpendicular pe suprafata conductorului:

.

Combinand acest rezultat cu legea inductiei

,

rezulta ca nu poate avea decat componente tangentiale la suprafata conductorului perfect:

.

Ca un corolar rezulta ca, la suprafata conductorilor perfecti, vectorii si sunt perpendiculari unul pe celalalt.

5. RELATII DE CONTINUITATE

Tinand seama de legile locale (1) si (3) si luand divergenta relatiei (1), se deduce :

.

Impunem ca marimile magnetice introduse sa verifice o ecuatiei de acelasi tip. Pentru aceasta scriem:

,

Semnul minus din fata termenului se explica prin aceea ca dorim ca legea de conservare sa fie de aceeasi forma ca in cazul electric:

.

In cazul sarcinilor utilizam aceleasi legi globale (1) si (3), dar deformam volumul elementar la o suprafata (fig.2) cu doua fete lipite (S₁ si S₂). Din (3) rezula

,

unde este divergenta superficiala a lui ; din (1) rezulta:

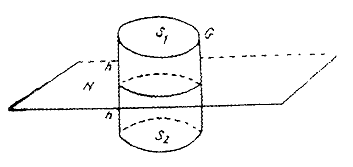
Fig.

Transpunand aceasta lege pentru marimile magnetice se obtine o relatie analoga. Daca se tine seama de posibilitatea acumularii unor sarcini superficiale prin aportul lui , se poate scrie

si o relatie analoga pentru marimile magnetice.

In mod analog, utilizand aceleasi legi, se arata ca subzista relatia:

una, formal identica, pentru marimile magnetice corespunzatoare.

Notand cu w densitatea de sarcina de linie, ecuatia de continuitate permite sa se obtina (fig.3), pentru ,

.

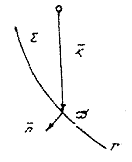
Fig. 3.

6.CONSIDERENTE SISTEMICE

Din punct de vedere al teoriei sistemelor, ecuatiile Maxwell dau relatii dintre variabilele terminale ale oricarui sistem electromagnetic. Prin variabilele asociate unui obiect O se intelege variabilele v₁,v₂,.,v_n intre care exista relatii de forma:

, (i=1,2,.),

ele fiind marimi caracteristice sistemului considerat.

Relatiile expuse in acest capitol nu epuizeaza relatiile dintre variabilele terminale, deoarece trebuie sa se tina cont si de legile de material care stabilesc legatura dintre si , si , , si . Exista si medii la care dependenta este inca mai complexa, relatiile stabilindu-se intre trei marimi terminale.

Necesitatea introducerii unor legi de material se poate justifica foarte simplu, tinand seama de numarul relatiilor si al variabilelor terminale. Vom considera pentru aceasta ecuatiile lui Maxwell sub forma locala si vom considera ecuatiile vectoriale pe componente. Rezulta ca in ecuatii intervin in total cinci marimi vectoriale (,,,,) si una scalara, ρ, deci in total 16 marimi scalare; numarul ecuatiilor scalare este opt. Evident ca din opt relatii scalare si reale nu se pot determina in general decat tot opt marimi scalare. Rezulta necesitatea de a se introduce alte legi in afara celor stabilite de Maxwell. Sarcina stabilirii acestor legi revine experientei, care descrie prin relatii proprietatile electrice ale substantelor.

In ceea ce priveste marimile de intrare si cele de iesire, trebuie observat ca se disting doua mari cazuri. In unele situatii se cunosc si ρ, care se considera marimi de intrare si se cer marimile de camp , , , , care, in acest caz, sunt marimi de iesire. Aceasta situatie se intalneste, de exemplu, la emitatoarele radio. La receptie, din contra, se cunoaste campul si se cere curentul produs de antena. In acest caz, marimile de intrare sunt marimile de camp , , si , iar marimile de iesire si ρ.

7.CLASIFICAREA MEDIILOR

Din punct de vedere al fenomenelor electromagnetice, mediile se pot clasifica in mai multe moduri. In aproape toate cazurile insa va fi vorba de relatiile dintre si , pe de alta parte, si marimile , si , pe de alta parte.

Mediile se numesc liniare daca relatiile dintre si , si ca si cele dintre si , sunt liniare. In cazul cel mai simplu,

, , ,

unde permitivitatea ε, conductivitatea σ si permeabilitate μ sunt constante scalare reale. In acest caz mediul se numeste izotop.

Daca una din cele trei constante macroscopice este un tensor de ordinul doi, mediul este din acel punct de vedere anizotrop.

Daca σ=0, mediul e pur dielectric sau nedisipativ, la el neexzistand transformari de energie electromagnetica in caldura prin efect Joule. Daca , mediul e disipativ, cu conductivitatea sau conductor .

Daca toate aceste trei constante macroscopice au aceeasi valoare in intreg spatiul, atunci mediul se numeste omogen. In caz contrar, el este neomogen.

In cazul fenomenelor electroagnetice cu variatie aronica in timp, vom scrie pentru o marime oarecare a campului:

,

relatie care defineste fazorul .

Pentru cimpuri electroagnetice avand o variatie armonica in timp, constantele macroscopice pot avea o valoare care sa depinda de frecventa, mediul e nedisipativ.

In unele cazuri, mediile prezinta fenomene de memorie, in sensul ca starea prezenta a mediului depinde de starile trecute.

De exemplu,

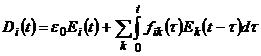
unde este un tensor de ordinul doi. Astfel de medii se numesc ereditare.

Mentionam, de asemenea, mediile cu polarizatie independente si nu intereseaza in studiul radiatiei si propagarii undelor electromagnetice daca au valori constante in timp.

Mediile la care nu exista o relatie liniara intre si si intre si se numesc neliniare.

In cazul mediilor cu ereditate, se admite de obicei ca tensorul este simetric, deci mediul este reciproc, in sensul ca admite aplicarea teoremelor de reciprocitate de tip Lorentz. Aplicand opoeratorul de transformare a lui Laplace, se obtine.

unde reprezinta transformata Laplace, iar

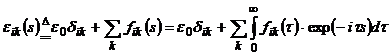
Anizotropia se poate manifesta si relativ la conductivitatea, legea lui Ohm modificandu-se in acest caz.

Daca se admite ca tensorul σ este simetric, atunci se exclud din tratarea unele clase de materiale, cum sunt de exemple, materialele care prezinta efect Hall.

In cazul unei variatii armonice in timp a marimilor de camp, indiferent de caracterul lor scalar sau tensorial, parametrii mediului pot fi reali sau complecsi. Daca sunt toti reali, mediul este fara vascozitate electromagnetica. In caz contrar, el prezinta o astfel de vascozitate. In general scriem:

, , ,

unde , nu sunt independente, fiind legate prin relatiile Kramers-Kronig.

8.MEDII BIANIZOTROPE

Aceste medii se caracterizeaza prin aceea ca vectorii si depind atat de , cat si de , fara a fi paraleli cu vreunul dintre ei. Notand cu c niteza luminii in spatiul liber, Cheng si Kong descriu mediile bianizotrope prin relatia matriceala

; ,

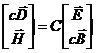unde P, Q, L si M sunt matrice . De exemplu, pentru un mediu girotropic stationar, mediu la care permitivitatea si permeabilitatea sunt marimi tensoriale, matricea C este:

,

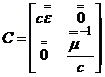unde si sunt formele matriceale ale tensorilor ε si μ, iar este matricea nula. Bianizotropia apare in conditii de laborator    la mediile in miscare, chiar daca acestea sunt izotrope fata de un referential fix.

9. REGIMUL ARMONIC

Un caz particular, dar deosebit de important, este constituit de regimul armonic, in care toate marimile campului variaza armonic cu aceeasi pulsatie ω. In acest caz, ecuatiile capului se scriu:

, ,

, ,

unde , , , iar , , .

In cazul mediilor liniare si izotrope

deci legile de evolutie devin:

sau

, ,

unde

.

Acest rezultat este important, aratand ca, in cazul regimului armonic, pentru mediile disipative ecuatiile campului electromagnetic pot capata forma pe care o au mediile fara pierderi, introducand permitivitatea echivalenta .

Trebuie remarcat faptul esential ca in regim armonic campul este complet descris de ecuatiile de evolutie si de legea de continuitate. Aplicand operatorul ecuatiilor de evolutie, se obtine:

de unde rezulta imediat Comparand cu legea continuitatii , rezulta Fiind vorba de un regim permanent, nu se mai pune problema determinarii unor constante C, ca in cazul studiat anterior.