MODELAREA NUMERICA A CURGERII IN TOBELE DE ESAPAMENT

Notiuni introductive in calculul dinamicii fluidelor

In calculul dinamicii fluidelor (CFD - COMPUTATIONAL FLUID DYNAMICS) contine metodele de calcul si analiza a sistemelor care cuprind curgerile fluidelor, transferul de caldura si fenomenele asociate, cum ar fi reactiile chimice cu ajutorul simularilor pe calculator.

Codurile CFD sunt structurate in jurul algoritmilor care pot aborda problemele de curgere a fluidelor. Pentru a furniza acces usor la toate facilitatile de rezolvare a pachetelor comerciale, CFD include intercalarea interferentelor sofisticate pentru introducerea parametrilor problema si sa examineze rezultatele. toate codurile contin in principiu trei elemente principale:

preprocesarea;

rezolvarea;

postprocesarea.

Metoda volumului finit a fost la origine o dezvoltare speciala a formularii prin diferente finite. Algoritmul numeric, in acest caz, consta in urmatorii pasi:

forma integrala a ecuatiilor de curgere a fluidului peste toate volumele de control ale domeniului de solutii;

discretizarea cuprinde substitutia unei variabile din ecuatiile integrale ale curgerii, reprezentand procese, cum ar fi: de convectie, difuzie si surse; acestea transforma ecuatiile integrale intr-un sistem algebric de ecuatii;

rezolvarea ecuatiilor algebrice printr-o metoda iterativa.

Codurile CFD contin tehnici specifice de discretizare pentru tratarea fenomenelor de transport, convectie (transport datorat curgerii fluidului) si difuzie (transport datorat variatiei variabilei de la punct la punct, precum si pentru termeni sursa (asociati cu aparitia si disparitia variabilei ) si viteza de schimb in unitatea de timp. Fenomenul fizic de ansamblu este complex si neliniar, asa ca se cer solutii de rezolvare iterative.

Modelarea curgerii gazelor prin tobele de esapament construite si a Daciei 1300, a fost realizata cu programul Fluent.

FLUENT furnizeaza o serie de capabilitati de modelare pentru o gama forte larga de curgeri incompresibile, laminare sau turbulente. In FLUENT, o gama larga de modele matematice pentru fenomene de transport (precum transferul termic sau reactiile chimice) este combinata cu abilitatea de a modela geometrii complexe.

Se pot modela moduri diferite de transfer termic, incluzand convectia naturala, fortata sau mixta cu sau fara considerearea medilor poroase sau a transferului de caldura conjugat, etc. Un set de modele de radiatie generale poat fi folosite pentru fenomenele complexe de combustie.

2.1 Ecuatia de conservare a masei

Ecuatia de conservare a masei sau ecuatia de continuitate, poate fi scrisa [15, 16, 47, 48]:

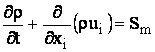(1)

2.2 Ecuatiile de conservare a miscarii

Conservarea miscarii in directia i fata de un sistem de referinta inertial (neaccelerat) este descrisa de

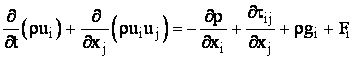(3)

unde p este presiunea statica, este tensorul tensiunilor (descris mai jos), si F_i sunt fortele gravitationale si cele exterioare pe directia i. F_i poate deasemenea sa contina si alti termeni in functie de modelul adoptat, cum ar fi spre exemplu influenta unui mediu poros.

2.3 Ecuatia conservarii energiei

FLUENT rezolva ecuatia de conservare a energiei in forma urmatoare [15, 16, 47, 4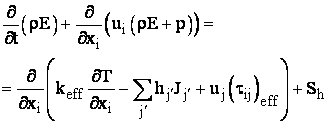8]:

(8)

unde     este conductivitatea efectiva (k + k_t, unde k_t is the conductivitatea termica turbulenta care este definita de modelul de turbulenta ales pentru curgere), iar J_j^' este fluxul difuziv al speciei j^'. Primii trei termeni din partea dreapta a relatiei (8) reprezinta trensferul de energie datorat conductivitatii termice, a difuzibilitatii speciilor si a disiparii vascoase. S_h include caldura reactiilor chimice si a celorlate surse termice considerate.

3 Modele de turbulenta utilizate in integrarea numerica

a ecuatiilor Navier-Stokes

3.1 Modelarea transferului de caldura si masa turbulent

Transportul turbulent al caldurii este modelat prin utilizarea conceptului analogiei Reynolds la transferul de impuls turbulent. Ecuatia "modelata" a energiei este data de

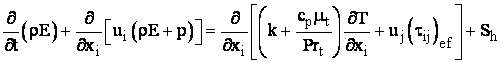(13)

unde E este energia totala iar este tensorul derivat al tensiunii, definit ca:

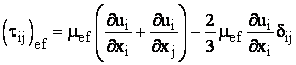(14)

Termenul ce include     reprezinta incalzirea vascoasa si este totdeauna necesar a fi calculat atunci cand se utilizeaza metoda de rezolvare cuplata. Valoarea implicita a numarului Prandtl turbulent este Pr 0.85. Transferul de masa turbulent este tratat similar cu transferul de caldura, utilizand pentru transferul de masa un numar Schmidt turbulent Sc = 0.7.

Conditiile la limita la perete pentru transportul scalar sunt tratate analog cu cele pentru impuls, utilizand o "lege la perete" corespunzatoare.

3.2 Modelul k-e standard

Modelul k-e standard este un model semi-empiric bazat pe modelarea ecuatiilor de transport pentru energia cinetica turbulenta (k) si viteza sa de disipare (e). Ecuatia de transport a modelului pentru k este derivata din ecuatia exacta, in timp ce ecuatia de transport a modelului pentru e a fost obtinuta utilizand considerente fizice, asemanandu-se foarte putin cu forma exacta a acestei ecuatii.

In formele derivate ale modelului k-e, s-a considerat curgerea complet turbulenta, iar efectele vascozitatii moleculare neglijabile; de aceea modelul k-e standard este validat doar pentru curgeri complet turbulente.

Ecuatiile de transport pentru modelul k-e standard

Energia cinetica turbulenta, k, si viteza sa de disipare, e, sunt obtinute din urmatoarele ecuatii de transport

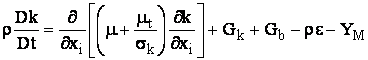(15)

si

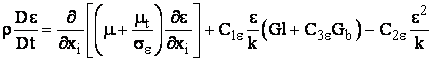(16)

5 Modelarea curgerii gazelor prin tobele de esapament

Considerand tobele prezentate in capitolul 7, s-au realizat modelele prezentate in figurile 3, 4 si 5. Intrarea gazului in domeniile considerate se realizaza prin sectiunile transversale ale tevilor, care contin originea sistemului de coordonate (v. cap. 7).

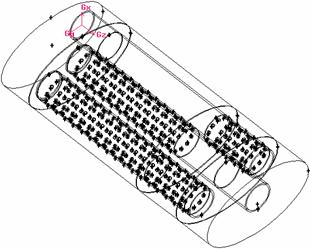
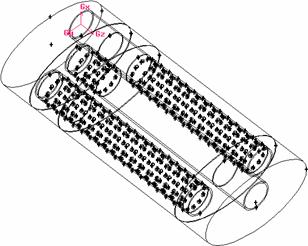
Fig. 3 Geometria variantei 1 Fig. 4 Geometria variantei 2

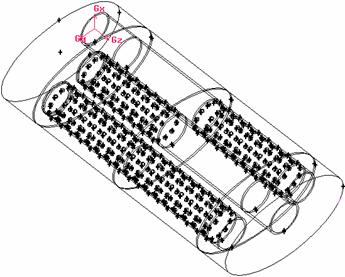
Fig. 5 Geometrie toba Dacie 1300

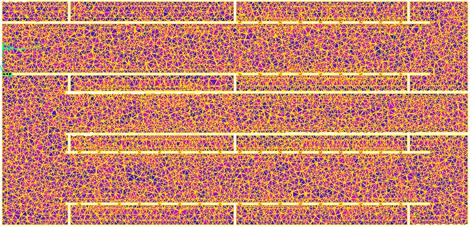
Fig. 6 Strat de elemente in sectiune prin planul yoz pentru toba de la Dacia 1300

Parametrii de intrare pentru toate cazurile s-au considerat:

viteza gazelor la intrarea in tobe: ;

temperatura de intrare a gazelor in tobe:

Se considera ca peretii care sunt in contact cu mediul exterior pierd cadula prin convectie, cu coeficientul , temperatura mediului ambiant fiind de 20 C.

Pentru peretii interiori se considera ca transferul este neglijabil.

Curgerea se considera stationara si turbulenta. Modelul de turbulenta ales este k-e

Pentru prezentarea rezultatelor s-au folosit 4 plane de sectiune. Planul 1 este planul sistemului de coordonate yoz. Planul 2 de sectiune este planul xoz (se observa ca acest plan contine axa conductei de intrare in toba). Planul 3 de sectiune este paralel cu planul xoz la cota y = 51,5 mm (se observa ca acest plan contine axa conductei. Planul 4 de sectiune este paralel cu planul xoz la cota y = 103 mm.

5.1 Cazul tobei varianta 1-a

In figurile 9, 10, 11 si 12 sunt prezentate distributiile vitezelor dupa planele de sectiune 1,2 3 si 4.

Fig. 9 Distributia de viteze in planul de sectiune 1

In figurile 13 este prezentat campul temperaturilor in planul de sectiune 1.

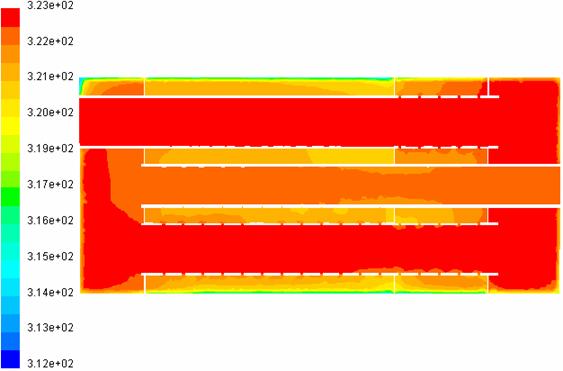
Fig. 13 Distributia de temperaturi in planul de sectiune 1

In figurile 15, 16, 17 si 18 sunt prezentate distributiile presiunii manometrice dupa planele de sectiune 1,2 3 si 4.

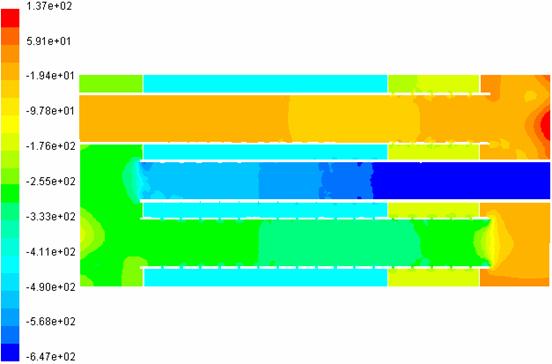
Fig. 15 Distributia presiunilor manometrice in planul de sectiune 1

5.2 Cazul tobei varianta 2-a

In figurile 20, 21, 22 si 23 sunt prezentate distributiile vitezelor dupa planele de sectiune 1,2 3 si 4.

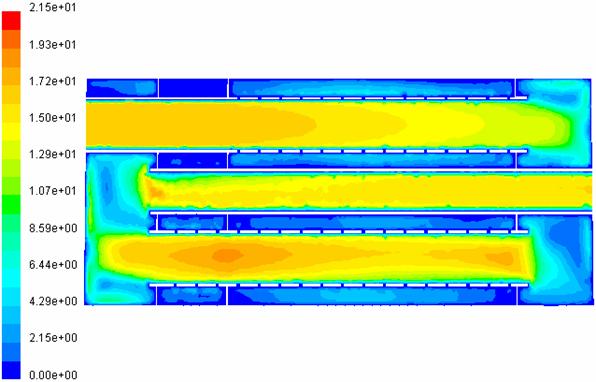
Fig. 20 Distributia de viteze in plan de sectiune 1

In figurile 24 este prezentat campul temperaturilor in planul de sectiune 1.

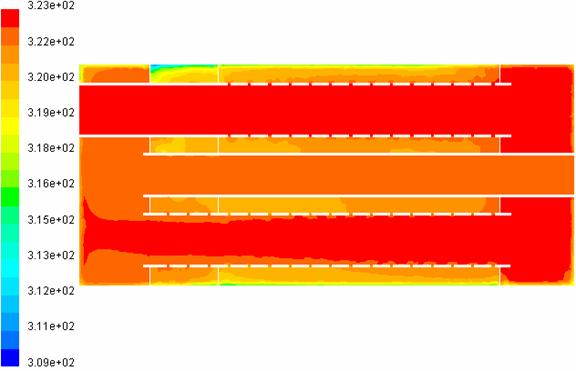
Fig. 24 Distributia de temperaturi in planul de sectiune 1

In figurile 26, 27, 28 si 29 sunt prezentate distributiile presiunii manometrice dupa planele de sectiune 1,2 3 si 4.

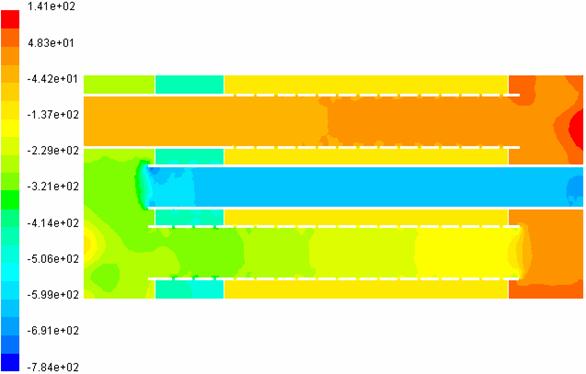
Fig. 26 Distributia presiunilor manometrice in planul de sectiune 1

5.3 Cazul tobei Dacia 1300

In figurile 31, 32, 33 si 34 sunt prezentate distributiile vitezelor dupa planele de sectiune 1,2 3 si 4.

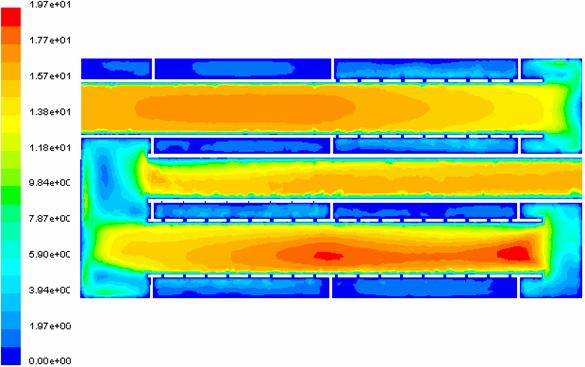
Fig. 31 Distributia de viteze in plan de sectiune 1

In figurile 35 este prezentat campul temperaturilor in planul de sectiune 1.

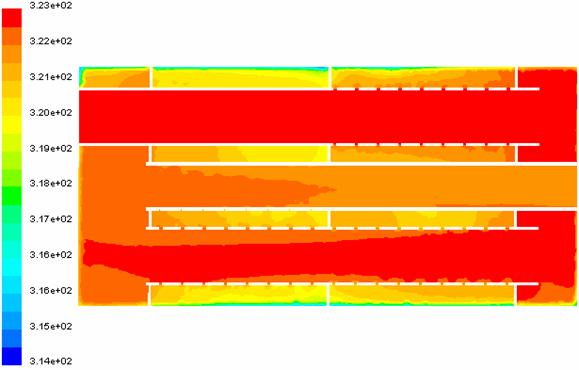
Fig. 35 Distributia de temperaturi in planul de sectiune 1

In figurile 37, 38, 39 si 40 sunt prezentate distributiile presiunii manometrice dupa planele de sectiune 1,2 3 si 4.

Fig. 37 Distributia presiunilor manometrice in planul de sectiune 1

Pentru varianta 1 se constata o cadere de presiune, intre sectiunea de intrare in toba si cea de iesire, de 647 . Pentru varianta a 2-a de toba, se constata o cadere de presiune intre sectiunile de intrare si de iesire, de 784 . Pentru toba de pe Dacia 1300 se constata o cadere de presiune de 706 .