Tensiuni electromotoare induse

Tensiunea electromotoare, de armonica j indusa intr-o infasurare monofazata, cuplata magnetic cu alte infasurari, se determina folosind legea inductiei electromagnetice

(2.83)

unde reprezinta fluxul total al infasurarii, datorat armonicilor spatiale de ordin j ale campurilor magnetice.

Considerand suprapunerea efectelor, expresia (2.83) a tensiunii electromotoare devine:

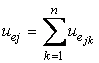(2.83.a)

unde este tensiunea electromotoare indusa de infasurarea k si are doua expresii:

Daca tensiunea este indusa de campul magnetic produs de o infasurare monofazata parcursa de curentul sinusoidal

,

atunci expresia tensiunii electromotoare este:

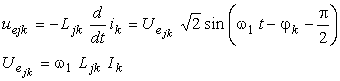(2.84.a)

unde reprezinta valoarea efectiva a tensiunii electromotoare induse de infasurarea k, iar este inductivitatea mutuala definita de relatia (2.76).

Daca tensiunea electromotoare este indusa de catre o unda magnetica progresiva de armonica spatiala j (2.79) atunci tensiunea electromotoare indusa are expresia:

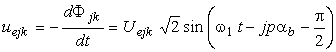(2.84.b)

(2.84.c)

unde este inductivitatea ciclica mutuala definita de relatia (2.79.a),

precizeaza pozitia infasurarii induse pe armatura, iar curentul care strabate faza de referinta a infasurarii inductoare este .

1. Tensiunile electromotoare induse de o unda magnetica progresiva in barele unei infasurari in colivie

Consideram o armatura rotorica care are o infasurare in colivie (vezi paragraful 1.1) formata in bare. In figura 2.31.a este prezentata o sectiune transversala prin rotor. Rotorul are lungimea si se deplaseaza intr-un camp magnetic invartitor de succesiune directa, de armonica spatiala j (2.63.a), care determina p poli magnetici:

(2.85)

unde amplitudinea are expresia (2.63.c).

Unda magnetica (2.85) este produsa de o infasurare polifazata, asezata pe stator, care este parcursa de un sistem polifazat, simetric si echilibrat de curenti; faza de referinta (faza 1) are axa magnetica suprapusa peste axa spatiala a armaturii (), iar curentul care o parcurge are expresia:

(2.85.a)

Rotorul are axa de referinta spatiala suprapusa peste axa crestaturii 1 (vezi figura 2.31.a) si se gaseste in miscare, in sensul crescator al coordonatei spatiale a statorului . Pozitia sa, la un moment dat este definita de unghiular (vezi figura 2.31.a).

Unda magnetica (2.85) se exprima in coordonata rotor , folosind schimbarea de variabila:

si are expresia:

(2.86)

unde s-a efectuat notatia:

(2.86.a)

In conformitate cu cele prezentate in paragraful 2.2.3.a se poate considera ca unda magnetica progresiva (2.86) poate fi produsa de o infasurare polifazata, dispusa pe rotor, avand axa magnetica a fazei de referinta suprapusa peste axa de referinta spatiala a rotorului. Infasurarea este alimentata cu un sistem simetric si echilibrat de curenti, curentul prin faza de referinta fiind:

(2.86.b)

Daca analizam desfasurarea in plan a coliviei (vezi figura 2.31.b), rezulta ca aceasta poate fi considerata ca fiind formata din bobine, fiecare avand o singura spira, constituita din doua bare succesive si portiunile aferente de inel. Deschiderea unghiulara a unei spire este . Axa bobinei de referinta (spira ABCD) - figura 2.31.b - formata din barele 1 si 2 si portiunile aferente de inel este deplasata inainte cu unghiul fata de axa de referinta spatiala a armaturii.

Tensiunile electromotoare induse de unda progresiva (2.86) in cele bobine ale infasurarii in colivie au expresiile (2.84.b):

(2.87)

unde este inductivitatea ciclica mutuala definita de relatia (2.79.a).

Pentru ca se neglijeaza efectele de capat, inductia magnetica este nula in zona inelelor. In consecinta tensiunea electromotoare indusa intr-o bobina este suma tensiunilor electromotoare din barele care formeaza bobina (vezi figura 2.31.b). Astfel se pot exprima tensiunile electromotoare din bare (avand ca indice numarul barei) in raport cu tensiunile electromotoare induse in bobine:

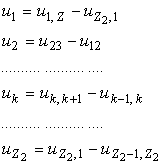(2.88.a)

Introducand (2.87) in (2.88.a) se obtin expresiile tensiunilor electromotoare din bare:

(2.88.b)

Expresiile tensiunilor (2.88.b) sugereaza posibilitatea echivalarii infasurarii in colivie avand bare, cu o infasurare dubla in stea cu faze si conductor de inchidere fictiv - vezi figura 2.18. Fiecare faza a acestei infasurari este formata dintr-o bara a colivie si cele doua portiuni de inele aferente.

Observatie

In cazul miscarii uniforme a rotorului, cu viteza unghiulara rezulta

si folosind egalitatile (2.86.b) si (2.69) se obtine:

(2.89)

unde alunecarea undei directe are expresia (2.69.a).

Aceleasi concluzii se obtin si in cazul in care unda magnetica progresiva este de succesiune inversa.