| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Schema lui Bernoulli cu bila intoarsǎ cu mai multe stǎri (multinomiala sau polinomialǎ)
Aceasǎ schemǎ de probabilitate este o generalizare a schemei binomiale. Se aplicǎ atunci cand la fiecare repetare a experimentului, se urmǎreste aparitia a r evenimante, care formeazǎ un sistem complet de evenimante. Probabilitǎtile de aparitie pentru evenimentele considerate nu depind de rangul repetǎrii, deci sunt constante. Se doreste calculul probabilitǎtii ca in n repetǎri independente ale experimentului, cele r evenimante precizate sǎ aparǎ de un numǎr de ori dat.
Modelul probabilistic este
realizat printr-o urnǎ ce contine bile
de r culori. Din urnǎ se
extrag, pe rand, bile cu intoarcerea bilei extrase in urnǎ, dupǎ ce
s-a constatat culoarea bilei extrase. Se cere sǎ se calculeze
probabilitatea![]() , ca din n bile
extrase
, ca din n bile
extrase ![]() sǎ fie de
culoarea intai,
sǎ fie de
culoarea intai, ![]() bile de culoarea a
doua s.a.m.d.
bile de culoarea a
doua s.a.m.d. ![]() sǎ fie de
culoarea a
sǎ fie de
culoarea a ![]() a.
a.
Folosind aceeasi metodǎ ca la schema binomialǎ, se obtine cǎ
![]()
unde ![]() sunt respectiv
probabilitǎtile de-a obtine la o extragere bilǎ de culoarea
sunt respectiv
probabilitǎtile de-a obtine la o extragere bilǎ de culoarea
![]()
Observatia 2.4 Daca se dezvolta urmatorul polinom
![]()
atunci probabilitatea ![]() este coefcientul
monomului
este coefcientul
monomului ![]() din aceasta dezvoltare. De aici si denumirea de
schema multinomiala sau polinomiala folosita pentru aceasta
schema de probabilitate.
din aceasta dezvoltare. De aici si denumirea de
schema multinomiala sau polinomiala folosita pentru aceasta
schema de probabilitate.
Observatia 2.5 Desigur ca au loc relatiile
![]() si
si ![]()
Exemplul 2.6. Piesele produse de
o masina sunt supuse la doua teste. Probabilitatile ca
o piesa sa treaca aceste teste sunt respectiv ![]() si
si ![]() . Vrem sa calculam probabilitatea ca din cinci
piese luate la intamplare, doua sa treaca ambele teste, una
numai al doilea test, iar una sa nu treaca nici un test.
. Vrem sa calculam probabilitatea ca din cinci
piese luate la intamplare, doua sa treaca ambele teste, una
numai al doilea test, iar una sa nu treaca nici un test.
Aceasta probabilitate se
calculeaza cu schema multinomiala, unde ![]() , iar daca se presupune ca cele doua teste
sunt independente, avem ca
, iar daca se presupune ca cele doua teste
sunt independente, avem ca
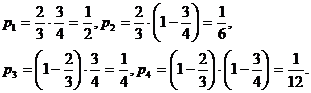
In acest fel putem scrie
![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 4876
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved