| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
||||
|
||||
In order to understand interference, recall that optical disturbances are described by second order, homogeneous, linear partial differential equations. This means that they obey the principle of superposition. Thus, the resultant electric field intensity, E, at a point in space where two or more waves overlap is equal to the vector sum of the individual constituent disturbances. This leads us to say that optical interference may be considered as an interaction of two or more light waves which yield a resulting flux that is different from the scalar sum of the component fluxes.
We have previously considered the problem of the superposition of two scalar waves, and these results will again be applicable here. However, light is a vector phenomenon; both the electric and magnetic field are vector quantities. Understanding this added level of complexity is crucial to understanding many optical phenomena.
Starting with the principle of superposition, the electric field intensity at a particular point in space is generated by the various fields, E1, E2, , of the constituent sources,
![]() (13.1)
(13.1)
For the sake of simplicity, consider two point sources, S1 and S2, emitting monochromatic waves of the same frequency in a homogenous medium. Let their separation a be much greater than l Locate the point of observation, P, far enough away from the sources so that at P the wavefronts will be planes. For now, consider only linearly polarized waves of the form
![]() (13.2)
(13.2)
and
![]() . (13.3)
. (13.3)
The irradiance at P is given by
 . (13.4)
. (13.4)
Recognizing that ![]() is the time average of
the square of the magnitude of the electric field intensity, we see that
is the time average of
the square of the magnitude of the electric field intensity, we see that
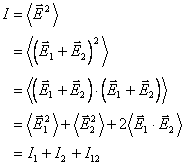 . (13.5)
. (13.5)
The last term is
known as the interference term. For the waves described by (13.2) and (13.3),
this can be evaluated as follows. First,
consider the effect of ![]() :
:
 . (13.6)
. (13.6)
Recall that the time average of a function f(t), taken over an interval T, is
![]() .
.
The period t
of a harmonic function is ![]() ; for this problem
; for this problem ![]() . After multiplying
out and averaging equation (13.6) we have
. After multiplying
out and averaging equation (13.6) we have
![]() , (13.7)
, (13.7)
where we used the
fact that ![]() ,
, ![]() , and
, and ![]() . The interference
term is then
. The interference
term is then
![]() , (13.8)
, (13.8)
where ![]() is the phase
difference. It comes from the
combined path length and the initial phase angle difference.
is the phase
difference. It comes from the
combined path length and the initial phase angle difference.
We can simplify our results in the
case of parallel amplitudes, ![]() . In this case,
equation (13.8) reduces to
. In this case,
equation (13.8) reduces to
![]() . (13.9)
. (13.9)
Using the fact that
![]()
and
![]() ,
,
this can be rewritten as
![]() , (13.10)
, (13.10)
so that the total irradiance becomes
![]() . (13.11)
. (13.11)
This reaches a maximum value of
 (13.12)
(13.12)
when ![]() , where
, where ![]() . In this case the
distributions are said to be in phase. This is known as total constructive interference. When
. In this case the
distributions are said to be in phase. This is known as total constructive interference. When ![]() , the waves are out of
phase,
, the waves are out of
phase, ![]() , and the condition is known as constructive interference. At
, and the condition is known as constructive interference. At ![]() ,
, ![]() , the optical disturbances are said to be 90 out of phase. For
, the optical disturbances are said to be 90 out of phase. For ![]() we get destructive interference,
we get destructive interference, ![]() . The minimum occurs
when
. The minimum occurs
when
 (13.13)
(13.13)
when ![]() , where
, where ![]() . This is known as total destructive interference.
. This is known as total destructive interference.
Another special case is when the amplitudes of both waves are equal. In this case the irradiances from both sources are equal, so let I1 = I2 = I0. Equation (13.11) can then be written as
 (13.14)
(13.14)
from which it
follows that ![]() and
and ![]() .
.
We have now discussed how two waves overlap to create an interference, or fringe, pattern. In order for this pattern to be observed, the two sources do not need to be in phase with each other. If there is some constant initial phase difference between the two sources, the resulting interference pattern will be identical to the original pattern, although it will be shifted in terms of the location of the minima and maxima. Such sources are said to be coherent. Remember that conventional quasimonochromatic sources produce light which is a mix of photon wavetrains. At each illuminated point in space there is a net field which oscillates through approximately a million cycles, which averages 10 ns or less, before it randomly changes phase. This interval over which the light wave resembles a sine function is a measure of its temporal coherence. Since the average time interval during which the wavetrain oscillates in a predictable manner is given by the coherence time, we see that the longer the coherence time, the greater the temporal coherence of the source.
In a similar way, if we observe the light wave from a fixed point in space, we see that it appears to be fairly sinusoidal for some number of oscillations between abrupt phase changes. The corresponding spatial extent over which the light wave oscillates in a regular, predictable way has already been identified as the coherence length. If we view the light beam as a progression of well defined sinusoidal wavegroups of average length DxC, whose phases are uncorrelated to one another, then we find that normal coherence lengths range from several millimeters for standard laboratory discharge tubes up to tens of kilometers for some lasers.
Two ordinary sources will normally maintain a constant relative phase for a time no greater than DtC, so the interference pattern that they produce will randomly shift around in space at an extremely rapid rate, averaging out and making it impractical to observe. Until the advent of the laser, it was generally accepted that no two individual sources would ever produce an observable interference pattern. The coherence time of lasers, however, is long enough so that interference of two independent lasers has been detected electronically.
If two beams are to interfere to produce a stable pattern, they must have nearly the same frequency. A significant frequency difference would result in a rapidly varying time dependent phase difference, which would cause I12 to average out to zero during the detection interval. If the sources both emit white light, the component reds will interfere with the reds, and the blues with the blues. A great many overlapping monochromatic patterns will be produces which combine to create a total white light pattern. This final pattern will not be as sharp or extensive as a monochromatic pattern, but white light will produce observable interference.
In addition to situations in which two coherent beams are combined to produce interference patterns, there are circumstances in which a much larger quantity of mutually coherent waves are made to interfere. To begin analyzing such a system, consider a glass plate, slightly silvered on both sides so that the reflection coefficients, the rs, are near unity. Assume that the silver film, substrate, and surrounding medium are transparent dielectrics, and let the film be nonabsorbing. For simplicity, let n1 = n2; this avoids the necessity of introducing different reflection and transmission coefficients at each interface.

Assume that the rays pass through a lens (not shown in the diagram), and focus at points P on the left side of the plate and at P on the right side of the plate. The optical fields at P are given by
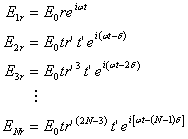 (13.15)
(13.15)
where ![]() is the incident wave.
is the incident wave.
The terms ![]() are the contributions
to the phase arising from the optical path length difference between adjacent
rays,
are the contributions
to the phase arising from the optical path length difference between adjacent
rays, ![]() . There is an
additional phase contribution arising from the optical distance traversed in
reaching point P, but this is common
to each ray and thus can be ignored. The
resultant reflected scalar wave is
then
. There is an
additional phase contribution arising from the optical distance traversed in
reaching point P, but this is common
to each ray and thus can be ignored. The
resultant reflected scalar wave is
then
 . (13.16)
. (13.16)
If ![]() , and if the number of terms in the series approaches
infinity, the series converges to
, and if the number of terms in the series approaches
infinity, the series converges to
![]() . (13.17)
. (13.17)
The reflected flux density at P is
 . (13.18)
. (13.18)
The amplitude of the transmitted waves are given by
 . (13.19)
. (13.19)
These can be added to yield
![]() . (13.20)
. (13.20)
In turn, this leads to the irradiance of the transmitted beam being given by
 . (13.21)
. (13.21)
Using the identity
![]() , and setting
, and setting ![]() , (13.18) and (13.21) can be rewritten as
, (13.18) and (13.21) can be rewritten as

and

or, defining the coefficient of finesse as
![]() ,
,![]() (13.22)
(13.22)
then
 (13.23)
(13.23)
and
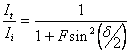 . (13.24)
. (13.24)
The term ![]() is known as the Airy function, and is denoted A(q).
It represents the transmitted flux density distribution. The complementary function, [1 - A(q)]
represents the reflected flux density distribution.
is known as the Airy function, and is denoted A(q).
It represents the transmitted flux density distribution. The complementary function, [1 - A(q)]
represents the reflected flux density distribution.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1499
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved