| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
1) GENERALITES.
Nous avons déjà abordé la notion de continuité dans la leçon précédente,
au cours des études locales pour les fonctions usuelles.
Rappelons les définitions générales énoncées à ce propos.
Une fonction f définie sur une partie I de R et à valeurs réelles est dite continue au réel x0 si et seulement ![]() .
.
Si f est continue en tout point de
lensemble I, on dira que f est
continue sur I
A)
Exemples, contre-exemples.
On a établi sans problÃmes que les fonctions polynômes, les
rationnelles, les fonctions sinus, cosinus, tangente, la fonction logarithme
Népérien, lexponentielle et les puissances de base quelconque sont continues
en tout point de leur ensemble de définition.
La continuité apparait donc au premier coup dœil comme un comportement
normal, du moins sur les fonctions classiques. Mais lensemble des fonctions
numériques déborde largement celui des fonctions dites élémentaires, décrites
ci-dessus.
Un premier exemple de phénomÃne de non-continuité en un point, on dira
plutôt de discontinuité, nous est donné en observant la fonction partie
entiÃre E qui fait correspondre à chaque réel x le plus grand entier relatif E(x)
inférieur ou égal à x.
_ Cette fonction est évidemment continue en tout réel non relatif, puisque la
restriction de E à un intervalle ouvert du type ]n, n+1[ avec nIZ est la fonction constante de valeur n.
_ Par contre en tout entier n la
limite à droite de E est encore n=E(n), tandis que la limite à gauche
est n-1, toujours daprÃs la
remarque sur la valeur n-1 de E sur ]n-1, n[.
On peut multiplier les exemples de ce type en raccordant par exemple
artificiellement deux courbes représentant des fonctions continues définies au
voisinage dun point mais dont les valeurs en ce point diffÃrent.
Par exemple si les fonctions u et v sont continues respectivement sur les
intervalles [c, a] et [a, d], la fonction f définie sur [c, d] par f(x)=u(x) si xI[c, a[
et f(x)=v(x)
si xI[a, d] satisfait
daprÃs les hypothÃses à : ![]()
Si u(a) est choisi différent de v(a), la fonction f ne présentera pas de limite au point a et ne sera donc pas continue en ce point. Par contre la
restriction de f à [a, d]
est continue en a car sa limite en ce
point, soit v(a), correspond exactement à la valeur de f en a.
On parle alors de continuité à droite de f en a.
On dira de mÃme que f est
continue à gauche en a si et
seulement si ![]()
Avec ces conventions on peut alors énoncer léquivalence pratique pour les études
de ce type :
f continue en a f continue à droite et à gauche en a ![]()
Remarquons à ce sujet que si une fonction f admet en un réel a
nappartenant pas à son ensemble de définition des limites à
droite et à gauche de mÃme valeur réelle l, on pourra prolonger f
en une fonction continue en a en lui
attribuant la valeur l en ce point..
On dit alors que lon a effectué un prolongement par continuité.
_ Dans les contre-exemples précédents, la discontinuité apparait comme un saut
brusque des valeurs de f au voisinage
du point détude, cest une rupture soudain de la courbe, un décrochage des
valeurs dont on peut avoir une intuition grossiÃre en imaginant une
marche que lon rate ou une ampoule électrique qui grille soudainement. (En
fait ce phénomÃne nous apparait discontinu bien que continu pour le
physicien mais à variations trÃs rapides, dans un intervalle de
temps inaccessible à nos sens, de mÃme quune projection
discontinu mais de cadence assez rapide dimages cinématographiques nous
donnera lillusion du mouvement continu auquel nous sommes habitués).
Il existe dautres façons de mettre en évidence une discontinuité, par exemple
en considérant une fonction nadmettant ni de limite à droite ni de
limite à gauche en ce point.
Ainsi la fonction f définie par f(x)=sin(![]() ) si x non nul et f(0)=0
est discontinue en 0.
) si x non nul et f(0)=0
est discontinue en 0.
Remarquons quici il ny a pas perte brusque de valeurs au voisinage
étudié mais plutôt des variations
damplitude constante dans des zones arbitrairement petites (tout lintervalle
[-1, 1] est décrit par les images, quel que soit le voisinage de 0 auquel on se
restreint).
_ Citons pour terminer un exemple de discontinuité totale. La fonction
caractéristique des rationnels, prenant la valeur 1 sur Q et 0 sur R Q nest continue en aucun réel.
B)
Opérations usuelles.
ThéorÃme. Soient f et g deux fonctions numériques définies sur
le mÃme ensemble I et continues en un point x0 de I. On Peut alors affirmer que la somme f+g, le produit f.g , le quotient ![]() (si g ne sannule pas sur I), sont également
continues au point x0.
(si g ne sannule pas sur I), sont également
continues au point x0.
La preuve est élémentaire et repose sur les rÃgles de calcul pratique
des limites.
Par hypothÃse on sait que ![]()
Ces limites
étant réelles on en déduit :
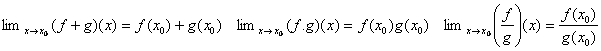
C)
ThéorÃme de composition.
Toute composée du type f![]() j
avec j continue en t0 et f
continue en x0=j(t0) est continue en t0
j
avec j continue en t0 et f
continue en x0=j(t0) est continue en t0
Par hypothÃse j
tend vers x0 en t0 et f tend vers f(x0)
en x0 .
On en déduit, daprÃs la rÃgle sur la limite dune composée, que ![]() , cest à dire que f
, cest à dire que f![]() j est
bien continue au point t0.
j est
bien continue au point t0.
2)
CONTINUITE SUR UN INTERVALLE.
La propriété de continuité devient particuliÃrement intéressante
lorsquelle est réalisée pour une fonction donnée f sur tout un intervalle I inclus dans son ensemble de définition.
Les effets cumulés des limites en chacun des points de I assurent alors
à la courbe de f une
régularité proche de lidée intuitive de continuité évoquée plus haut (pas de
perte de valeurs, pas de saut brusque), pouvant se résumer en disant que f(I) est encore un intervalle de R, de type fermé borné si I est lui
mÃme un fermé borné.
Létude rigoureuse est abordée en détail dans les théorÃmes suivants
dont les démonstrations reposent essentiellement sur laxiome de la borne
supérieure pour les parties majorées de R A)
ThéorÃme des valeurs intermédiaires.
Soit f fonction à valeurs réelles, continue en
tout point de lintervalle [a, b] de R.
Toute valeur réelle y comprise entre
les deux images f(a) et f(b) admettra au moins un
antécédent pour f situé dans
lintervalle [a, b].
Preuve : Il sagit donc de montrer que
léquation f(x)=y, de paramÃtre y intermédiaire entre les valeurs f(a)
et f(b), admet au moins une solution appartenant
à [a, b].
Cette équation équivaut à f(x)-y=0.
En remplaçant f par la différence g=f-y , on se ramÃne donc
à une équation standard du type g(x)=0, avec g toujours continue sur [a, b]
(différence entre f continue sur cet
intervalle et la fonction constante de valeur y) et telle que les images de g
aux bornes a et b de lintervalle soient de signe contraire. ( ceci venant de la
condition : y intermédiaire
entre f(a)
et f(b)
)
Quitte enfin à remplacer éventuellement g par g , on pourra
toujours se ramener au cas oà g(a) sera négatif ou nul et g(b)
positif ou nul.
Notons alors E lensemble des éléments x
de [a, b] tels que g(x) £0.
_ E est non vide car il contient au moins a
par hypothÃse sur le signe de g
aux bornes.
_ E est majoré de maniÃre évidente par b.
E possÃde donc une borne supérieure que lon notera c, plus petit majorant possible pour E.
La fonction g étant continue sur tout [a,
b] sera en particulier continue en c.
Analysons en sappuyant sur cette propriété le signe de g en ce point.
_ Supposons dabord g(c) strictement positif. On pourra alors trouver un voisinage V de cette
image ne contenant que des nombres strictement positifs.
Puisque g a pour limite g(c)
en c, on pourra trouver un
voisinage W=]c-a, c+a tel que g(W [a, b]) ÌV.
Or c étant le plus petit majorant
possible de E, c-a qui lui est strictement
inférieur ne peut majorer E. Il existe donc au moins un élément x de E tel que c-a < x £
c.
Cet x étant élément de W [a, b] on devrait donc
avoir g(x) IV,
donc strictement positif, ce qui est en contradiction avec lappartenance de x à E (caractérisée par g(x)
£0)
g(c)
ne peut donc Ãtre strictement positif.
_ Si g(c) est strictement négatif..
Suivant le mÃme schéma de continuité en c on pourra trouver un voisinage V de g(c) inclus dans ]-¥, 0[ et un voisinage W=]c-a, c+a tel que g(W [a, b]) ÌV.
Puisque g(c) <0
et g(b) ³0,
c est strictement inférieur à b. On pourra donc en restreignant
éventuellement W, se ramener au cas oà c+a est
lui aussi strictement inférieur à b.
Remarquons alors que tout élément x
de [c, c+a[ a
son image par g strictement négative
donc est élément de E. Mais ceci est en contradiction avec le fait que c majore E. On ne peut en effet trouver
déléments de E strictement supérieurs à c.
g(c)
ne peut donc non plus Ãtre strictement négatif.
La seule possibilité est donc g(c)=0, ce qui assure lexistence dune
solution pour léquation étudiée.
B)
Image dun intervalle fermé borné par une fonction continue.
Si la fonction f à valeurs réelles est continue en tout point de
lintervalle fermé borné [a, b] de R, alors limage f([a, b])
est aussi un intervalle fermé borné [m,
M] avec :
m=inf et M=sup
Montrons dabord que f est bornée sur
[a, b]. Le processus sera voisin de la méthode précédente et repose sur
lidée : jusquoà peut on aller sur [a, b] en gardant la
propriété analysée vérifiée ?
Ainsi on notera E lensemble des éléments x
de [a, b] tels que f soit bornée
sur [a, x]
E est évidemment non vide, (il contient a !)
et est majoré par b. On peut donc
parler de la borne supérieure c de E.
Par continuité de f au point c de [a, b], on pourra trouver
un voisinage W=]c-a, c+a[ pour
lequel f(W [a,
b])Ì ] f(c)-1, f(c)+1[. La restriction de f à W [a, b] sera donc bornée.
c-a étant strictement inférieur au
plus petit majorant c de E ne sera
pas majorant de E .
Il existe donc un élément x de E tel
que c-a < x £
c.
Par caractérisation mÃme des éléments de E, f est alors bornée sur [a, x].
Or on vient de voir quelle est bornée sur ]c-a, c+a [a, b]. Elle est donc
bornée sur la réunion des intervalles mentionnés, donc aussi sur le sous
intervalle [a, c] de cette réunion.
Le point c est donc élément de
E . (Ceci nétait pas assuré car la borne supérieure dun ensemble nest
pas nécessairement élément de cet ensemble)
_ Si c=b, le résultat est
établi : f est bien bornée sur [a,
b].
_ Si c <b. On pourra alors en diminuant au
besoin la valeur a, se
ramener au cas oà c+a <b
Mais dans ce cas on sait que f bornée sur [a, c] et sur [c, c+a[. On en déduit que f sera bornée sur la réunion de ces intervalles, donc aussi sur la
partie [a, c+![]() ].
].
Le point c+![]() est alors élément de E et strictement supérieur à la
borne supérieure c de cet ensemble E,
ce qui est contradictoire.
est alors élément de E et strictement supérieur à la
borne supérieure c de cet ensemble E,
ce qui est contradictoire.
Seule lhypothÃse précédente c=b est donc réaliste, f est bien bornée sur [a, b]
Montrons maintenant que la borne supérieure M=sup des valeurs de f sur
[a, b] est en fait une valeur effective de la fonction, atteinte en un
point de lintervalle.
Nous emploierons pour cela une méthode classique dite de dichotomie, reposant
sur des divisions successives de lintervalle initial I0=[a, b].
_ PremiÃre étape. Considérons c=![]() le milieu de lintervalle I0. La fonction f étant bornée sur I0 est
donc également bornée sur chacune des deux parties [a, c] et [c, b].
le milieu de lintervalle I0. La fonction f étant bornée sur I0 est
donc également bornée sur chacune des deux parties [a, c] et [c, b].
Posons M1=sup et M2=sup. On vérifie trÃs
facilement que la borne supérieure M
de f sur I0 nest autre
que la plus grande des deux bornes précédentes, soit M=max(M1, M2). Une de ces deux bornes
au moins coÃncide donc avec M.
Notons alors I1=[a, c] si M1=M et I1=[c, b]
sinon.
Dans les deux cas apparait un sous intervalle I1=[a1, b1] de I0,
de longueur ![]() , et tel que lon ait M=sup.
, et tel que lon ait M=sup.
_ Poursuite du procédé. On peut répéter lopération de division précédente
à partir de lintervalle I1. On mettra donc en évidence un
sous intervalle I2=[a2,
b2] de I1, de
longueur ![]() , et tel que lon ait encore M=sup
, et tel que lon ait encore M=sup
Il est clair que lon peut récidiver en divisant maintenant I2, puis
poursuivre suivant le mÃme schéma aussi loin que lon veut.
On construit donc de proche en proche une suite dintervalles emboités, n a In=[an,
bn], de longueurs
respectives l(In)=![]() et tels que pour tout n : M=sup.
et tels que pour tout n : M=sup.
La suite de réels n aan est alors croissante, (puisque In+1 Ì In pour tout n) et majorée par b, donc
va converger vers un élément l de [a, b].
Supposons que f(l)
<M et considérons un réel l tel que f(l) <l < M.
Par continuité de f en l, pour tout e >0 il existe un voisinage W=]l-a, l+a[ de l tel que f(W [a, b]) Ì] f(l)-e, f(l)+e[.
Si on utilise ceci pour e l- f(l), on aura donc : x I]l-a, l+a [a, b] Þ f(x) <l.
La suite n aan convergent vers l, il va exister un rang n1 tel que n ³n Þ anI]l-a, l+a[
Mais la suite n abn converge aussi vers l puisque ![]()
On pourra donc trouver aussi un rang n2 tel que n ³n Þ bnI]l-a, l+a[.
Pour tout entier n supérieur à
n1 et n2, lintervalle [an,
bn] sera donc contenu entiÃrement dans le voisinage ]l-a, l+a[. On en déduit daprÃs le
choix de ce voisinage : f(In)Ì ¥ l]
M ne peut donc Ãtre la borne
supérieure de f sur In puisque lon a un majorant l des images de f sur cet intervalle strictement
inférieur à M. Ceci est en
contradiction avec le choix de In.
LhypothÃse f(l)
<M est donc à rejeter. Puisque f(l)
£M borne supérieure des images de f,
on aura nécessairement f(l)=M.
On démontrerait de mÃme que la borne inférieure m de f sur [a, b]
est également atteinte par f en un
point de cet intervalle. (On peut aussi appliquer le résultat précédent
concernant la borne supérieure à la fonction continue f , car inf=-sup
On savait déjà f([a,
b])Ì [m , M]. Le
théorÃme des valeurs intermédiaires appliqué à f sur un intervalle dont les bornes sont
des antécédents respectifs de m et M nous donne linclusion inverse [m, M]
Ì
f([a, b]).
On a donc bien f([a,
b])=[m, M].
C)
Inversion dune fonction continue strictement monotone.
ThéorÃme :
Soit I un intervalle quelconque de R, de bornes a et b (éléments de R ).
Si f est une fonction continue sur I,
à valeurs réelles, strictement monotone sur I, on peut alors
conclure :
_ f(I)=J est un intervalle de bornes c=![]() et d=
et d=![]() . avec en plus les équivalences : c IJ a II et d
IJ b II.
. avec en plus les équivalences : c IJ a II et d
IJ b II.
_ f relie bijectivement I à J et la
bijection réciproque est continue en tout point de J.
Nous effectuerons létude sous lhypothÃse oà f est strictement croissante sur
lintervalle I.
On se ramÃnera à ce cas si f
est décroissance en considérant g = -f .
1) Supposons dabord que I est un intervalle fermé borné I=[a, b].
Le théorÃme précédent assure alors que f([a, b]) est égal à
[ f(a), f(b)]
puisque les bornes inférieures m et M de f
sur [a, b] ne sont autres ici , vu la croissance de f, que les valeurs de cette fonction aux extrémités de lintervalle
en question.
Tout élément de J=[ f(a), f(b)]
admet donc un antécédent au moins pour f
sur [a, b] et un seul vu la stricte croissance de f. En effet (x,
y) I [a, b] [a, b], : x <y f(x) < f(y)
ce qui assure linjectivité.
Pour la continuité de la réciproque f
1, considérons un point y0
de J et x0=f 1(y0).
_ Si y0 est distinct des
bornes de J, x0 sera
distinct des bornes de I, et tout voisinage V de ce point contiendra un
voisinage fondamental ]x0-e, x0+e[ inclus entiÃrement dans ]a, b[.
On aura alors, vu la stricte croissance
de f , léquivalence suivante :
x0-e < x < x0+e f(x0-e < f(x)< f(x0+e)
Si W=]y0-a, y0+a[ est un voisinage de y0 inclus dans ] f(x0-e), f(x0+e)[, on en déduit daprÃs ce qui précÃde
limplication : yIW Þ x=f
1(y) IV.
Le schéma de la continuité en y0
est donc vérifié.
_ Si y0 est une des bornes
de J, il suffit dadapter légÃrement la démonstration ci dessus en
tenant compte que lon étudie uniquement la limite à droite en f(a) si y0 est cette image ou la limite à gauche si y0= f(b).
Par exemple dans le premier cas on choisira e tel que [a, a +e Ì [a, b[ V, pour VIV(a) donné, puis W=[ f(a) ,
f(a)+a[ inclus dans [ f(a),
f(a+e)[.
2) Considérons maintenant un intervalle du type I=[a, b[ avec a réel. En considérant une suite
strictement croissante n abn de réels de I convergent vers b, on constate que I nest autre que la
réunion croissante des In=[a, bn].
En effet tout réel x tel que a £x <b pourra Ãtre dépassé par un
des termes bn pour un rang
n assez grand.
On peut alors écrire : ![]() =
=![]()
Or la suite de réels n a
f(bn) étant croissante admet
une limite d pour n tendant vers +¥, réelle si f majorée sur I, égale à +¥ sinon.
Dans les deux cas on en déduit facilement f(I)=[
f(a), d[=J
Linjectivité vient encore bien sÃr de la stricte croissance.
La continuité de f 1
sétablit comme dans le cas précédent. On pourrait aussi dire que pour tout y0 de J et tout voisinage V
de ce point on pourra trouver un entier n
tel que [f(a), f(bn)] contient V J . La continuité de la
restriction de f 1
à [ f(a), f(bn)]
est alors assurée vu la premiÃre étude, donc aussi la continuité de f 1 en y0 vu la localité de la
notion de limite.
3) Les autres configurations dintervalles se traitent suivant des schémas
analogues.
D)
Monotonie dune bijection continue reliant deux intervalles.
ThéorÃme :
Si f est une bijection continue reliant lintervalle I à lintervalle J, alors f est strictement monotone sur cet intervalle.
Il sagit dun semblant de réciproque de létude précédente. La démonstration
repose essentiellement sur le théorÃme des valeurs intermédiaires.
Nous considérerons pour commencer un point a
arbitraire de I, distinct des bornes de cet intervalle.
Il existe donc un élément b de I
strictement supérieur à a, et
dont limage sera bien sÃr distincte de celle de a par injectivité de f.
Nous allons voir que si f(b)
>
f(a), f
sera nécessairement strictement croissante sur I. (Le cas oà f(b) <
f(a) se traitera en considérant g=-f
et conduira à la stricte
décroissance de f).
1) Commençons par montrer que pour tout x
de I : x >a Þ f(x) > f(a).
Raisonnons par labsurde et soit x >a tel que f(x) < f(a).
_ Lélément x ne peut appartenir
à [a, b], sinon, daprÃs le théorÃme des valeurs
intermédiaires, il existerait au moins un réel c de [x, b] tel que f(c)= f(a), ( puisque f(a) serait comprise entre f(x)
et f(b).).
Légalité f(c)
= f(a) serait alors contraire à linjectivité de f.
_ De mÃme x ne peut Ãtre
strictement plus grand que b, car il
existerait un c entre b et x
tel que f(c)= f(a). On a donc bien établi limplication
mentionnée plus haut.
2) Soit maintenant x et y
de I tels que a <x <y.
Supposons f(x)
>
f(y).
_ Si f(a)
<
f(y) il existera alors, toujours
daprÃs le théorÃme des valeurs intermédiaires, un réel c de [a, x] tel que f(c)=
f(y) ce qui est contraire
à linjectivité.
_ Si f(y)
<
f(a), f(a)
est alors intermédiaire entre f(x)
et f(y).
La fonction f devra donc prendre la
valeur f(a)
en un point c de [x, y]
ce qui nie encore linjectivité de f.
On a donc établi la stricte croissance de f
sur lintervalle [a, +¥ I.
3) Remarquons maintenant quil est impossible de trouver deux éléments x et y
de I tels que :
x <y <a et f(x) > f(y).
En effet en procédant comme précédemment on pourrait en déduire que f est strictement décroissante sur I [x, +¥[
ce qui nest pas conforme avec f
croissante sur lintervalle [a, +¥ I.
f est donc bien croissante
strictement sur I ¥, a] et sur I [a,
+¥[, donc sur I entier.
E)
Image dun intervalle quelconque par une fonction continue.
ThéorÃme :
Limage dun intervalle quelconque I de R par une fonction continue sur I à valeurs réelles est encore un intervalle de R
Ici aucune hypothÃse sur le sens de variation de f.
Le résultat a déjà été établi dans le cas oà I est un intervalle
fermé borné.
Examinons une configuration du type I=]a,
b[. Il est facile décrire un tel
intervalle comme réunion strictement croissante dune suite dintervalles
emboités In=[an, bn].
Posons pour tout entier n : f([an,
bn])=[cn, dn].
On peut alors écrire : f(I)=![]() =
=![]()
En appelant c la limite de la suite
décroissante n a
cn et
d celle de la suite croissante n a dn
(Limites éventuellement infinies), on peut vérifier facilement que f(I)
est un intervalle dont les bornes sont c
et d.
Plus précisément on aura :
_ c I f(I) la suite n a cn
est stationnaire (constante à partir dun certain rang)
_ d I f(I) la suite n a dn
est stationnaire (constante à partir dun certain rang)
Les autres cas se traitent en utilisant des recompositions analogues de I en
réunion dintervalles emboités .
Exercices sur la continuité.
Etudier
la continuité des fonctions définies sur R
par les formules suivantes :
a) xIR- f(x)=![]()
b) xIR- f(x)=(x-p)sin(![]() ) et f(p)=0
) et f(p)=0
c) x £0 f(x)=![]() et x> f(x)=
et x> f(x)=![]()
Etudier
la continuité des fonctions définies par les formules suivantes :
a) Sur ]1,+¥[
f(x)=![]() et sur ]-¥,1[
et sur ]-¥,1[ ![]()
b) Sur R- f(x)=![]() et f(3)=1
et f(3)=1
c) xIQ f(x)=x-![]() et xIR Q
f(x)=0
et xIR Q
f(x)=0
On
considÃre la fonction f
définie par :
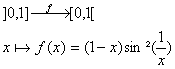
a) f est-elle continue sur
]0,1] ?
b) Peut-on prolonger f en une
fonction continue sur [0,1] ?
c) f est-elle injective ?
surjective ?
f désigne une fonction à valeurs dans R , continue sur [0,+¥[ et telle que f(0)=1
Etudier les problÃmes aux limites
en 0 et +¥
pour les fonction g et h définies
sur ]0,+¥[
par les formules respectives :
![]() ;
; ![]()
On
considÃre f définie sur ]0,+¥[ par le procédé suivant :
_ Si x rationnel a pour représentant
irréductible ![]() , alors f(x)=
, alors f(x)=![]() .
.
_ Si x est irrationnel f(x)=0.
Montrer que f est continue en tout
irrationnel et discontinue en tout rationnel
Soit f une fonction à valeurs
réelles, continue sur [0,+¥[ .
a) Montrer que si f admet une limite
réelle en +¥,
f est nécessairement bornée sur ¥ b) Montrer que si f est périodique, f est également bornée sur ¥ mais nadmettra de limite en +¥ que si cest une fonction
constante.
Soit
f une fonction de [a, b]
dans [a, b] telle que x
¹y : ![]()
Montrer que léquation f(x)=x admet alors toujours une et une seule
solution sur [a, b]
Soient
f et g deux fonctions à valeurs réelles, continues sur [0, ¥ et telles que pour tout x réel : 0 < f(x)< g(x).
a) Montrer que pour toute suite n axn déléments de [0, 1] on a :
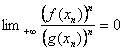
b) Montrer à laide dun contre-exemple précis que le résultat précédent
nest plus nécessairement vrai si la suite n
axn nest plus supposée bornée.
On
considÃre une fonction f
à valeurs réelles, continue sur [0,+¥[, avec f(0)=1 et telle quau voisinage de +¥ on ait léquivalence : f(x) x².
Montrer quil existe au moins un point M de la courbe C représentant f dans un repÃre cartésien
dorigine O tel que le milieu I de (O, M) appartienne aussi à C.
f
désigne une
fonction à valeurs réelles, strictement croissante sur ]a,
b[ et telle que limage par f de
]a, b[ soit un intervalle du type ]c,
d[.
Montrer que f est continue sur ]a,b[.
A toute fonction f à valeurs réelles définie sur R on associe la fonction g définie par :
xIR g(x)=[f(x)]²- f(x)
a) Montrer que si f est continue sur R, alors g est aussi continue sur R.
b) Donner un contre-exemple précis montrant que g peut Ãtre continue sur R entier sans que f
ne le soit.
c) On suppose g continue sur R et f
à valeurs strictement
supérieures à ![]() .
.
Montrer que sous ces hypothÃses f
est alors aussi nécessairement continue sur R entier.
f
et g désignent deux fonctions à
valeurs réelles, continues sur lintervalle [a, b] et telles que f([a, b])Ì g([a, b]).
Montrer quil existe au moins un point x
de [a, b] pour lequel f(x)=g(x).
a) Quelles sont les fonctions f à valeurs réelles continues sur
R telles que pour tout x réel on ait légalité : (f(x))²= f(x).
b) Déterminer toutes les fonctions à valeurs réelles, continues à
droite sur [0,+¥[
et telles que pour tout x réel :
f(x)=
f(x²).
a) Montrer que pour tout nombre
rationnel x>0 il existe un et un seul réel
que lon notera f(x)
tel que f(x)I]0,![]() [ et x- f(x) soit un multiple de
[ et x- f(x) soit un multiple de ![]() avec un coefficient
entier.
avec un coefficient
entier.
b) On considÃre alors lapplication f
à valeurs dans ]0,![]() [ qui à tout x de A=Q ¥[ fait correspondre lélément f(x) défini précédemment. Montrer que f est injective, non surjective et
continue en tout point de A.
[ qui à tout x de A=Q ¥[ fait correspondre lélément f(x) défini précédemment. Montrer que f est injective, non surjective et
continue en tout point de A.
c) Soit g la réciproque de la
restriction de f à lensemble
darrivée B=f(A). Montrer que g est discontinue en tout point de B.
On considÃre une fonction f à valeurs réelles, continue sur [0,+¥[ et telle que pour tout réel positif x on ait f(2x)+ f(x) =0. Montrer que f est la fonction nulle sur [0,+¥
f désigne une fonction continue
sur [0,+¥[,
à valeurs réelles et telle que
a) xI[0,1] f(x)=x(x+1)
b) La courbe C représentant f dans un
repÃre cartésien admet une asymptôte oblique au voisinage de +¥ de coefficient directeur ![]() .
.
Montrer quil existe au moins un réel x>0 tel que ![]() .
.
On considÃre une fonction f de ]0, 1] vers R satisfaisant aux deux propriétés suivantes :
a) la fonction g définie sur ]0,1]
par x ag(x)=f(x)-f(![]() ) est continue en tout point.
) est continue en tout point.
b) xI]0,10-6[ f(x)=![]()
Montrer que f est continue sur ]0,
1].
On considÃre une fonction f à valeurs réelles continue sur
[0, 1], avec f(0)=0 et f(1)=1. On
suppose aussi que la courbe C représentant f
dans un repÃre cartésien dorigine O est toute entiÃre au dessus
de la droite (OA) ; A désignant le point de coordonnées (1, 1).
Montrer que quel que soit le réel t
de [0, 1] il existe au moins deux points M et N de la courbe C tels que ![]() .
.
On considÃre une fonction f continue et strictement décroissante
sur [0, 1], à valeurs dans ce mÃme intervalle [0,1].
a) Montrer que pour tout entier non nul n
il existe un et un seul réel de [0, 1] que lon notera xn , pour lequel f(xn)=(xn)n.
b) Montrer que la suite n axn est croissante et converge vers
1.
Soit f une bijection continue de [0, 1] sur [0, 1].
On considÃre lapplication g
de [0,1] vers [0,1] définie par la formule : ![]()
Lapplication g est-elle
bijective ?
Solutions des exercices sur la continuité.
a)
Pour x ¹0 : 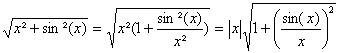
Ainsi f admet ![]() pour limite à
droite en 0 et -
pour limite à
droite en 0 et -![]() comme limite à gauche.
comme limite à gauche.
f nest pas continue en 0, elle nest
continue quà droite en ce point.
En tout autre point x0 on
peut restreindre létude à un voisinage ne contenant pas lorigine et
sur lequel f sera définie par x a f(x)=![]() donc continue daprÃs la continuité des fonctions
usuelles et les rÃgles opératoires.
donc continue daprÃs la continuité des fonctions
usuelles et les rÃgles opératoires.
b) xIR ![]() . On en déduit daprÃs le théorÃme
dencadrement que
. On en déduit daprÃs le théorÃme
dencadrement que ![]() La fonction f est bien continue au point p.
La fonction f est bien continue au point p.
En tout autre x0 on peut
comme précédemment se restreindre à un voisinage oà f sera définie par la formule x a f(x)=(x-p)sin(![]() ) . La continuité est donc assurée daprÃs les
théorÃmes sur les produits et composées de fonctions continues.
) . La continuité est donc assurée daprÃs les
théorÃmes sur les produits et composées de fonctions continues.
c) Il est clair que f est continue
à gauche en 0, le quotient étudié ne présentant pas dindétermination.
Pour létude à gauche il suffit décrire x >0 f(x)=![]()
Il vient bien alors aussi : ![]()
En x0 non nul, la
continuité sétablit sans problÃme comme dans les questions précédentes
en utilisant le principe de localité.
a)
La restriction de f à ]1, +¥[ est une fonction rationnelle x a![]() continue en tout point distinct du pôle 1. De mÃme la
restriction de f à ]-¥, 1[ est la composée dune fraction rationnelle
par la fonction racine carrée donc est également continue sur ]-¥, 1[.
continue en tout point distinct du pôle 1. De mÃme la
restriction de f à ]-¥, 1[ est la composée dune fraction rationnelle
par la fonction racine carrée donc est également continue sur ]-¥, 1[.
Chacun des deux intervalles en question contenant un voisinage fondamental de
chacun de ses points, le principe de localité assure la continuité de f sur la totalité de son ensemble de
définition R-.
Remarquons que le problÃme de continuité ne se pose pas en 1 qui nappartient
pas à lensemble de définition de f.
Par contre, f tendant vers +¥ en 1, il est clair quon ne peut
prolonger la fonction donnée en une application continue sur R entier.
b) Il est facile détablir que f
nadmet pas de limite au point 3. Il suffit de considérer dune part la suite n aan=3+![]() convergent vers 3 avec
convergent vers 3 avec ![]() et dautre part la
suite n a bn=3+
et dautre part la
suite n a bn=3+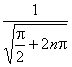 pour laquelle
pour laquelle ![]()
f nest donc pas continue au point 3,
mais lest en tout autre point en invoquant à nouveau le principe de
localité et la continuité des fonctions rationnelles et du sinus.
c) _ Tout rationnel x0 est
limite de la suite de rationnels n aan=x0+![]() et aussi limite de la suite dirrationnels n a bn=x0+
et aussi limite de la suite dirrationnels n a bn=x0+![]() .
.
Par définition de f, on a f(an)=an-![]() qui tend donc vers x0-
qui tend donc vers x0-![]() ¹0 lorsque n
tend vers +¥ et f(bn)=0
de limite nulle pour n tendant vers +¥. La fonction donnée nest donc
continue en aucun nombre rationnel x0.
¹0 lorsque n
tend vers +¥ et f(bn)=0
de limite nulle pour n tendant vers +¥. La fonction donnée nest donc
continue en aucun nombre rationnel x0.
_ Soit maintenant x0 un
irrationnel. Il est facile en utilisant la fonction partie entiÃre E, de
définir une suite de rationnels convergent vers x0.
Il suffit de poser pour tout n non
nul : an=![]() .
.
On a en effet n IN* E(nx0)
£ nx0 < E(nx0)+1
par définition de la partie entiÃre, doà lon tire
lencadrement : ![]() .
.
On a donc une suite convergent vers x0
dont la suite des images n a
f(an)=an-![]() converge vers x0
-
converge vers x0
-![]() .
.
Puisque f(x0)=0, f
sera discontinue en tout irrationnel distinct de ![]() .
.
Par contre en ![]() la continuité est
assurée par la majoration
la continuité est
assurée par la majoration ![]() , valable pour tout réel x.
, valable pour tout réel x.
f est donc seulement continue au
point ![]() .
.
a)
f est bien continue sur ]0,1] en tant
que produit dune fonction affine par le carré de la composée de la fonction
rationnelle x a![]() avec le sinus.
avec le sinus.
b) On ne peut prolonger par continuité f en 0 car la fonction nadmet pas de limite en
ce point. Il suffit pour voir cela de considérer les deux suites de termes
généraux respectifs
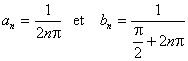 convergentes vers 0 et
dont les images par f tendent respectivement vers les limites
différentes 0 et 1.
convergentes vers 0 et
dont les images par f tendent respectivement vers les limites
différentes 0 et 1.
c) f nest pas injective, tous les
inverses des multiples entiers de p ont pour image 0.
Par contre elle est surjective. En effet, utilisons la suite n abn ci dessus pour laquelle ![]() . Pour tout y de [0, 1[ on peut donc trouver un
entier n tel que y < f(bn) <1. Le nombre y est donc situé entre limage par f de bn et f(1)
=0.
. Pour tout y de [0, 1[ on peut donc trouver un
entier n tel que y < f(bn) <1. Le nombre y est donc situé entre limage par f de bn et f(1)
=0.
La fonction f étant continue sur [bn, 1], le théorÃme
des valeurs intermédiaires assure lexistence dun antécédent de y pour f sur cet intervalle.
a)
Pour x >0 : 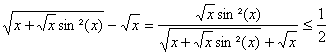
Pour x ³ 0, la différence étudiée ci
dessus appartient donc toujours à lintervalle [0, ![]() ].
].
f étant supposée continue sur [0,+¥[ sera donc bornée sur le fermé
borné [0, ![]() ].
].
Le numérateur de g est donc borné et
son dénominateur tend vers +¥ en + ¥. On en déduit que g tend vers 0 en +¥.
_ Pour létude en 0, toujours par continuité de f : ![]()
Le dénominateur de g tendant vers 0
par valeurs positives, il vient : ![]()
b) Au voisinage de +¥
, sin(f((x)) est négligeable, car bornée, devant 3x qui tend vers +¥.
Par continuité de f, limage f([0,1])
est un intervalle fermé borné. f(sin²(x)) est donc aussi négligeable devant x au voisinage de +¥.
On en déduit que h(x) est équivalente en +¥ au quotient de 3x par x, donc a pour limite 3.
_ En 0 la fonction h est continue
daprÃs les rÃgles opératoires sur les fonctions continues et le
théorÃme de composition. ![]()
_
Montrons dabord que f est
discontinue en tout rationnel strictement positif donné sous forme irréductible :![]() . En un tel point, par définition de f, on a f(x0)=
. En un tel point, par définition de f, on a f(x0)=![]() .
.
Examinons la suite dirrationnels positifs n
aan=x0+![]() . Elle converge de maniÃre évidente vers x0 , mais la suite des images
n a
f(an) stagne en 0 donc ne converge pas vers f(x0). La fonction étudiée est donc discontinue en x0.
. Elle converge de maniÃre évidente vers x0 , mais la suite des images
n a
f(an) stagne en 0 donc ne converge pas vers f(x0). La fonction étudiée est donc discontinue en x0.
_ Soit maintenant x0 un
irrationnel strictement positif donné. Un tel point a son image par f nulle. Pour un réel a >0 quelconque, examinons les rationnels
de lintervalle ]x0 , x0 +a[
Il en existe toujours, par exemple les approximations décimales de x0 à a prÃs par excÃs.
Considérons lensemble des représentants irréductibles de ces fractions
dentiers et notons q0 la
plus petite valeur possible pour les dénominateurs.
Pour tout rationnel ![]()
Le numérateur de la fraction encadrée ci dessus est un entier non nul donc au
moins égal à 1, quand au dénominateur, on peut le majorer par q² daprÃs le
caractÃre minimal de q0.
On en déduit : ![]() et par suite
et par suite ![]()
Pour tout réel e >0 on pourra donc trouver un
intervalle du type [x0 , ![]() tel que pour tout x de cette zone on ait 0 £
f(x) < e .
tel que pour tout x de cette zone on ait 0 £
f(x) < e .
Il suffit de choisir ![]() correspondant à
létude ci dessus pour la valeur a e .
correspondant à
létude ci dessus pour la valeur a e .
On aura en effet pour x rationnel de [x0 , ![]() , 0 < f(x).<
, 0 < f(x).<![]() et pour x irrationnel
f(x)=0 La fonction f est donc continue à droite en x0.
et pour x irrationnel
f(x)=0 La fonction f est donc continue à droite en x0.
La continuité à gauche sétablit par un raisonnement similaire.
a) En revenant à la définition originelle de la limite, on est sÃr
de lexistence dun voisinage V de +¥ tel que f(V ¥ Ì ]l-1, l+1[ , donc de
lexistence dun réel a >0 tel que f soit bornée sur [a, +¥[. (En désignant par l la limite réelle de f en +¥)
Limage dun intervalle fermé borné par une fonction continue étant encore un
fermé borné, f sera également borné sur [0, a] et donc aussi daprÃs ce qui
précÃde, sur la réunion [0,a] [a,+¥ ¥[
b) Soit t une période de f, cest
à dire un réel strictement positif tel que x ³0 f(x+t)=f(x)
f étant supposée continue sur R transformera lintervalle [0,t] en un
intervalle fermé borné J=[m , M] de R. Vu la périodicité, on démontre
trÃs facilement par récurrence que J est aussi limage de tout
intervalle du type [nt, (n+1)t] pour n entier quelconque.
On a donc, puisque R+ est la réunion de tous ces
intervalles : f([0,+¥[)=[m, M]
Pour x réel positif donné, la suite n a x+nt
tend vers +¥.
Si f admettait une limite l en +¥ on devrait donc avoir, daprÃs
le théorÃme de composition : ![]() .
.
Or la suite des images en question est stationnaire en f(x), ceci vu la périodicité de f
.
Un tel schéma nest donc possible que si f
est constante sur [0,+¥
Soit
x0 un élément donné de I=[a, b].
DaprÃs la propriété vérifiée par f
on peut écrire que pour tout x de I
distinct de x0 : ![]() .
.
On en déduit, daprÃs le
théorÃme dencadrement que : ![]()
La fonction f est donc continue sur
I.
La fonction g définie sur le
mÃme intervalle par x ag(x)= f(x)-x
est continue comme différence de deux fonctions continues. Examinons ses
valeurs aux bornes.
g(a)=f(a)-a ³0 et g(b)=
f(b)-b £0
, car les valeurs de f appartiennent
par hypothÃse à [a, b]
Le théorÃme des valeurs intermédiaires appliqué à g assure donc déjà lexistence
dun point c de I oà g va sannuler, cest à dire pour
lequel f(c)=c.
LhypothÃse de majoration stricte sur I, soit ![]() montre quun tel point
est nécessairement unique. En effet appliquée à x=c et y=d deux points
supposés fixes pour f, on en déduit
linégalité
montre quun tel point
est nécessairement unique. En effet appliquée à x=c et y=d deux points
supposés fixes pour f, on en déduit
linégalité ![]() , contradictoire si c distinct de d.
, contradictoire si c distinct de d.
a)
La fonction h définie sur [0,+¥[ par x ah(x)=![]() est continue comme quotient de deux fonctions continues.
Elle transforme donc lintervalle fermé borné [0, 1] en un intervalle du
mÃme type, soit [a, q].
est continue comme quotient de deux fonctions continues.
Elle transforme donc lintervalle fermé borné [0, 1] en un intervalle du
mÃme type, soit [a, q].
La borne q étant une valeur effective
de h, il existe un réel c ³0 pour lequel ![]() .
.
Puisque 0 <f(c)<g(c) par hypothÃse , on en déduit 0<q<1.
On montrerait de mÃme que a >0.
Ainsi, pour tout entier n on aura 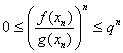 , puisque tous les termes xn
sont à valeurs dans [0, 1] et ont par suite leur image par h appartenant à [a, q].
, puisque tous les termes xn
sont à valeurs dans [0, 1] et ont par suite leur image par h appartenant à [a, q].
Puisque 0<q<1, on en déduit ![]() , puis
, puis 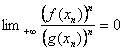 daprÃs le
théorÃme dencadrement.
daprÃs le
théorÃme dencadrement.
b) Comme contre-exemple on peut considérer f(x)=x+1 ; g(x)=x+2 et xn=n-1 pour n ³1
On remarque alors que 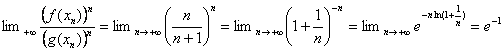
(En utilisant léquivalent élémentaire au voisinage de 0 : ln(1+h)
h
Prenons
pour inconnue labscisse x du point M
cherché dans le repÃre proposé.
Les coordonnées de M sont alors (x, f(x)) et celles du milieu I de (O, M) sont
![]()
La contrainte sur lappartenance de I à la courbe C se traduit alors par
léquation ![]() , elle mÃme équivalente à
, elle mÃme équivalente à ![]()
Considérons donc la fonction g définie
sur [0,+¥[
par g(x)= ![]()
_ g est continue en tout point par
continuité de f sur [0,+¥[ et grace aux théorÃmes
généraux de la théorie (rÃgles opératoires, théorÃme de
composition).
_ La valeur de g en 0 est la seule
calculable exactement : g(0)=
f(0)-2f(0)=-1
_ Etudions maintenant g au voisinage
de +¥.
Par hypothÃse on peut écrire au V(+¥) : f(x)=x²+o(x²).
On en déduit ![]()
et par suite g(x)=![]() sera équivalente à
sera équivalente à ![]() au voisinage de +¥.
au voisinage de +¥.
On en déduit que g sera du signe de x² , strictement positive au
voisinage de +¥,
donc prendra des valeurs positives sur un intervalle du type [a, +¥[.
Le théorÃme des valeurs intermédiaires assure alors lannulation de g en au moins un point de [0, a] puisque g reste continue sur cet intervalle et prend des valeurs de signes
différents aux bornes.
Soit x0 un élément de ]a,
b[ et [ f(x0)-e, f(x0)+e] un intervalle de centre f(x0)
inclus dans
]c,
d[. (Tout voisinage fondamental de f(x0) en contient
nécessairement un de ce type, il suffit puisque c < f(x0)
< d de choisir e >0 suffisamment petit.)
Puisque ]c, d[= f(]a, b[)
, il existe deux réels x1
et x2 de ]a, b[
dont les images respectives par f
sont f(x0)-e et f(x0)+e, avec de plus x1 < x0
<x puisque f est supposée strictement croissante.
Cette mÃme croissance permet de conclure : x1 < x
<x Þ
f(x1) <
f(x) <
f(x2).
Ainsi si on choisit le réel a tel que le voisinage V=]x0-a, x0+a[ soit inclus dans ]x1, x2[,
on aura bien f(V) Ì ] f(x0)-e, f(x0)+e[.
Ce schéma justifie que ![]() , donc établit la continuité de f en tout point.
, donc établit la continuité de f en tout point.
a) La fonction f étant supposée continue sur R, g=f f
- f le sera également daprÃs les
théorÃmes sur le produit et la différence de fonctions continues.
b) Les contre-exemples sont nombreux ! On peut par exemple obtenir la
fonction g identiquement nulle
à partir de f ne prenant
exclusivement que lune des deux valeurs 0 ou 1 sans Ãtre constante. Une
telle fonction ne satisfait pas à la propriété des valeurs
intermédiaires et ne peut donc Ãtre continue sur R entier.
Par exemple f nulle sur ]-¥,0[ et égale à 1 sur [0,+¥[ sera discontinue à
lorigine.
c) Le procédé de définition de g
montre que pour tout réel x fixé, f(x) est une des solutions de léquation
du second degré dinconnue X : X²-X-g(x)=0
La demi somme de ces deux racines (point milieu) est égale à ![]()
Sous lhypothÃse supplémentaire que f
ne prend que des valeurs supérieures à ![]() ,
,
f est nécessairement définie sur R entier par la seule formule : ![]()
f
sera donc continue sur R daprÃs la continuité de g, de la fonction racine carrée et grace
aux théorÃmes classiques de la théorie (compositions, sommes, produits
de fonctions continues. )
Si on considÃre la
fonction d définie sur [a, b]
par d(x)= g(x)-
f(x) , continue comme différence
de deux fonctions continues, la question posée revient à établir que d sannule au moins une fois sur [a, b].
DaprÃs le théorÃme des valeurs intermédiaires, il suffit alors
de trouver deux points de lintervalle oà g a des images de signe différents.
Considérons pour cela des nombres a et b oà g atteint respectivement ses bornes inférieures m et supérieures M sur [a, b]. Ils existent effectivement, puisque
limage dun fermé borné par une fonction continue est encore un intervalle de
ce type.
g([a, b])=[m, M]=[ g(a), g(b)].
Vu lhypothÃse f([a,
b])Ì g([a, b])=[m,
M], il est clair maintenant que d(a)=m- f(a £0 et que d(b)=M-
f(b ³
a) Sur R : (f(x))²= f(x)
f(x) I.
Une fonction non constante ne prenant sur R que ces deux valeurs ne peut donc Ãtre continue sur R entier, ceci daprÃs le
théorÃme des valeurs intermédiaires.( Elle devrait prendre aussi toute
valeur de [0, 1].)
Il ny a donc que deux fonctions possibles, celle identiquement nulle et la
constante 1.
b)
_ Soit x un réel de [0, 1[. DaprÃs lhypothÃse sur f on peut écrire la chaine
dégalités :
f(x)= f(x²)= f(x4)=f(x8)=
..=![]()
Or la suite n a![]() converge vers 0 par valeurs supérieures puisque 0 £x <1.
converge vers 0 par valeurs supérieures puisque 0 £x <1.
Par continuité à droite de f
en 0, on en déduit lim+ ¥ ![]() f(0)
f(0)
Ainsi sur [0,1[ : f(x)=
f(0) par unicité de la limite.
_ LhypothÃse sur f peut se traduire également sous la
forme :
x ³0 , f(x)= f(![]() )
)
Par répétition de cette variante on en déduit alors :
f(x)=
f(![]() )= f(
)= f(![]() )= f(
)= f(![]() )=
.= f(
)=
.= f(![]() )=
..
)=
..
Si on prend maintenant x >1, la suite n a![]() converge vers 1 par valeurs supérieures.
converge vers 1 par valeurs supérieures.
La continuité de f à droite en
1 permet donc ici de conclure que sur ]1,+¥[ f(x)= f(1)
f doit donc Ãtre constante sur [0,1[ et
sur ]1,+¥[.
Ce sont les seules solutions possibles.
(On vérifie aisément que toutes ces fonctions vérifient la contrainte : xI ¥[ f(x²)= f(x) et sont bien continues à droite en tout point de [0, +¥
a) On veut décomposer tout
rationnel strictement positif x sous
la forme x=y+n![]() avec n entier et 0
<y <
avec n entier et 0
<y <![]() . Cette écriture équivaut à
. Cette écriture équivaut à ![]()
Lentier n cherché doit donc vérifier
lencadrement : 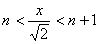
Ceci caractérise n comme le plus
grand entier inférieur ou égal à ![]() cest à dire
à la partie entiÃre de ce quotient que nous noterons E(
cest à dire
à la partie entiÃre de ce quotient que nous noterons E(![]() ).
).
Du fait que x est supposé rationnel
non nul, ![]() ne pourra Ãtre
entier et lencadrement de ce nombre par
les entiers n=E(
ne pourra Ãtre
entier et lencadrement de ce nombre par
les entiers n=E(![]() ) et n+1 sera bien
strict.
) et n+1 sera bien
strict.
Il sensuit que z=![]() - n est bien
élément de ]0,1[.
- n est bien
élément de ]0,1[.
La décomposition de x est donc
toujours possible et unique avec n=E(![]() ) et y=
) et y=![]() z .
z .
Ceci peut se résumer par la formule : y= f(x)=x-![]() E(
E(![]() ) .
) .
b) _ f
injective. Soient x et x deux éléments de A ayant mÃme
image par f. Vu la formule
définissant cette fonction on en déduit aussitôt x-x=![]() (E(
(E(![]() )-E(
)-E(![]() )).
)).
Or ![]() est irrationnel et x-x rationnel, légalité nest donc
possible que si les deux membres sont nuls.
est irrationnel et x-x rationnel, légalité nest donc
possible que si les deux membres sont nuls.
_ f
non surjective. Tout élément de ]0,![]() [ du type y=l
[ du type y=l![]() avec l rationnel na pas dantécédent pour f. En effet on ne pourra trouver de
rationnel x et dentier n tels que
avec l rationnel na pas dantécédent pour f. En effet on ne pourra trouver de
rationnel x et dentier n tels que
x=l![]() +n
+n![]() =(l+n)
=(l+n) ![]()
_ f
continue sur A. Soit x0 un
point de A et n0 la partie
entiÃre de ![]() .
.
Lintervalle I=]n0![]() , (n0+1)
, (n0+1)![]() [ contient un voisinage fondamental V de x0 puisque ce point appartient à I. Pour tout x de A V on a alors E(
[ contient un voisinage fondamental V de x0 puisque ce point appartient à I. Pour tout x de A V on a alors E(![]() )=n0 et par suite f(x)=x-n0
)=n0 et par suite f(x)=x-n0![]()
f est donc localement affine au
voisinage de x0 , donc est
continue en ce point.
c) Gardons les notations ci dessus et considérons une suite de rationnels n arn convergent vers ![]() par valeurs
supérieures.
par valeurs
supérieures.
De f(x0)=x0 n0![]() on déduit immédiatement : n IN x0+rn=f(x0)
+(n0+1)
on déduit immédiatement : n IN x0+rn=f(x0)
+(n0+1) ![]() + rn-
+ rn-![]()
Puisque ![]() , il existe un rang
à partir duquel les termes de cette suite seront bien éléments de ]0,
, il existe un rang
à partir duquel les termes de cette suite seront bien éléments de ]0, ![]() [, auquel appartient y0.
[, auquel appartient y0.
A partir de ce rang, par définition mÃme de f, on aura alors : f(x0+rn)= f(x0)+rn-![]() .
.
En utilisant la réciproque g de f restreinte à lensemble
darrivée B, on peut donc écrire par définition dun antécédent : g(y0+rn-![]() )=x0+rn
)=x0+rn
Il vient donc : ![]()
Cette limite est différente de g(y0)=x0. Ceci entraine la discontinuité de g en y0
puisque la suite n ay +rn-![]() converge vers le point y0.
converge vers le point y0.
Pour x=0 la relation sécrit 2f(0)=0
et donne donc f(0) nul.
Remarquons que léquation vérifiée par f
peut se traduire aussi par : x ³0, f(x)=- f(![]() )
)
En appliquant cette relation en cascade, on en déduit la suite
dégalités :
f(x)=-![]()
Or ![]() par continuité de f. On a donc bien : x I ¥[ f(x)=0.
par continuité de f. On a donc bien : x I ¥[ f(x)=0.
Le problÃme posé se
ramÃne à léquation f(x)f(![]() )-1=0.
)-1=0.
Considérons donc la fonction g
définie sur ]0,+¥[
par la formule g(x)=f(x)f(![]() )-1.
)-1.
Cette fonction est continue en tout point vu la continuité supposée de f et les théorÃmes classiques sur
les sommes, produits, composées de fonctions continues.
Compte tenu du théorÃme des valeurs intermédiaires, son annulation en au
moins un point sera établi si on prouve que g
ne garde pas un signe constant sur son intervalle détude.
_ 1 est le seul point x oÃ
lon sait exprimer de maniÃre exacte les images par f de x et ![]()
On trouve f(1)=1(1+1)=2 et g(1)=3
_ Au voisinage de +¥
on peut écrire par hypothÃse un développement asymptotique du type :
f(x)=![]() avec b constante réelle.
avec b constante réelle.
Pour x >1 on a 0 < ![]() <1
, doà lon déduit f(
<1
, doà lon déduit f(![]() )=
)=![]() (
(![]() +1)
+1)
Ainsi, au voisinage de +¥ : g(x)=(![]() )
)![]() (
(![]() +1)-1=
+1)-1=![]()
Ainsi g tend vers -![]() en +¥ et verra donc nécessairement toutes ses
valeurs négatives pour x assez grand.
en +¥ et verra donc nécessairement toutes ses
valeurs négatives pour x assez grand.
La fonction g change de signe et
sannule donc au moins une fois sur [1,+¥[
Remarque : x >0 g(x)=g(![]() ). g sannule donc aussi en un point de
]0,1[.
). g sannule donc aussi en un point de
]0,1[.
Notons j la fonction de ]0,1] vers ]0,1]
définie par la formule j(x)=![]()
La composée g![]() j est continue en tant que composée de deux
fonctions continues et est caractérisée par la formule x a f(
j est continue en tant que composée de deux
fonctions continues et est caractérisée par la formule x a f(![]() )-f(
)-f(![]() )
)
Plus généralement, pour tout entier n,
la composée g![]() jn est continue sur I=]0,1] et associe
à tout x limage
jn est continue sur I=]0,1] et associe
à tout x limage ![]() .
.
Par sommation, la fonction ![]() est donc continue sur
I et est définie par la formule
est donc continue sur
I et est définie par la formule ![]()
Pour tout x de I on a : 0 <![]() £
£
![]() .
.
Or, les puissances de 2 sont supérieures à 106 dÃs que
lexposant atteint la valeur 20.
On en déduit que sur I la fonction S19 est définie par la
formule :
![]() . Ceci entraine la continuité de f , en tant que somme de la fonction continue S19 avec la composée x
asin(
. Ceci entraine la continuité de f , en tant que somme de la fonction continue S19 avec la composée x
asin(![]() ) de fonctions usuelles continues.
) de fonctions usuelles continues.
Prenons pour inconnues les
abscisses respectives x et y des points M et N cherchés.
Le vecteur ![]() a donc (y-x, f(y)-
f(x)) comme couple de composantes
et légalité vectorielle
a donc (y-x, f(y)-
f(x)) comme couple de composantes
et légalité vectorielle ![]() se traduit par le
systÃme :
se traduit par le
systÃme : ![]()
Par substitution il vient donc y=x+t et f(x+t)- f(x)=t
Notons alors g la fonction définie
sur lintervalle I=[0, 1-t] par g(x)= f(x+t)- f(x)-t
g est évidemment continue sur I par
continuité de f et grace aux
théorÃmes sur la somme et la composée de fonctions continues. Examinons
les valeurs de g aux bornes de I.
g(0)= f(t)-t est positif. car lhypothÃse C
au dessus de (OA) se traduit : uI[0, 1] f(u) ³u
g(1-t)=1- f(1-t)-t= (1-t)- f(1-t) est donc négatif pour la mÃme
raison géométrique.
On peut donc conclure, avec le théorÃme des valeurs intermédiaires,
à lannulation de g en un
point au moins de I. Il existe donc bien un couple de points (M, N) de la
courbe C réalisant la contrainte ![]()
a) Pour tout entier n non nul notons gn la fonction définie sur I=[0,1] par gn(x)=f(x)-xn
Cette fonction est continue en tant que différence de deux fonctions continues
sur I.
Or gn(0)=f(0) est positif et gn(1)=f(1)-1
est négatif puisque f est à
valeurs dans [0, 1]
Il existe donc, daprÃs le théorÃme des valeurs intermédiaires,
un point au moins oà gn
sannule. Ce point est en fait unique car gn
est strictement décroissante sur I comme somme de deux fonctions strictement
décroissantes.
b) DaprÃs la définition de la suite étudiée, on a pour tout entier n non nul les égalités successives :
f(xn)=(xn)n
et f(xn+1)=(xn+1)n+1.
Remarquons dabord que les termes de cette suite sont à valeurs dans ]0,
1[.
En effet les égalités f(0)=0 et f(1)=1 sont impossibles vu
la stricte décroissance de f et le
fait que les valeurs de celle ci sont entre 0 et 1.
Supposons xn ³ xn+1. On en déduit par monotonie de f , linégalité f(xn) £ f(xn+1), soit encore
daprÃs les égalités précédentes : (xn)n £ (xn+1)n+1.
Or (xn+1)n+1 < (xn+1)n car xn+1
I]0,1[.
On en tire, daprÃs la relation précédente, linégalité xn <xn+1 contradictoire avec lhypothÃse de départ.
La suite en question est donc strictement croissante.
DaprÃs le théorÃme de convergence monotone, la suite croissante n axn a pour limite le réel l de I avec l=sup. On a donc pour tout n : 0 <(xn)n £ (l)n
Si l était strictement inférieur
à 1, on en déduirait que la suite n
a(xn)n
converge vers 0.
Or cette suite nest autre que celle des images n a f(xn) qui doit converger vers f(l) par continuité de f en
l.
Lunicité de la limite entraine f(l)=0
ce qui est impossible vu la stricte décroissance de f. (on aurait f(1) <0)
La seule possibilité est donc la convergence vers l=1.
f
réalisant une
bijection continue de I=[0, 1] sur lui mÃme, elle est soit strictement
croissante avec f(0)=0 et f(1)=1, soit strictement
décroissante avec f(0)=1 et f(1)=0
_ Dans le premier cas, la fonction g
définie par g(x)=![]() est de maniÃre évidente continue et strictement
croissante sur I comme somme de deux fonctions continues strictement
croissantes. Elle réalise donc une bijection de I sur [g(0), g(1)]=[0, 1]
est de maniÃre évidente continue et strictement
croissante sur I comme somme de deux fonctions continues strictement
croissantes. Elle réalise donc une bijection de I sur [g(0), g(1)]=[0, 1]
_ Dans le deuxiÃme cas, la continuité est encore assurée, mais plus la
monotonie.
Prenons par exemple pour f la
fonction affine x a
f(x)=1-x.
La fonction g construite à
partir de celle-ci nest autre que la fonction constante x a g(x)=![]()
On ne peut donc conclure à la bijectivité de g lorsque f est décroissante.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2423
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved