| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
THEORIE DE LA DIMENSION
1)
SYSTEMES LIBRES, GENERATEURS, BASES.
Rappelons
les définitions déjà posées dans le chapitre précédent. Un
systÃme S=(e1, e2,
, en) de n
vecteurs du K espace E est dit générateur de E
si et seulement si tout vecteur v de
E peut sécrire comme combinaison linéaire des vecteurs de S. Si de plus la
décomposition de chacun des vecteurs de E est unique, on dit que S est une base
du K-espace E.
On peut présenter différemment ces notions en associant à S
lapplication K-linéaire f du
K espace standard Kn vers E définie par : xIKn f(x)=![]() .
.
Notons les traductions évidentes :
S générateur de E
f est surjective.
S base de E
f est bijective.
Linjectivité de f na pour linstant
pas fait lobjet dune définition particuliÃre. Nous allons combler ce
vide en appelant systÃme libre tout systÃme S pour lequel f satisfait à linjectivité, ou
encore, puisque f est une application
K-linéaire, tout systÃme S
pour lequel Ker(f) est réduit au zéro
de Kn.
Ceci se résume donc à :
S=(e1,
e2,
, en) Libre le seul jeu x=(x1,
, xn) de coefficients de K tel que ![]() est
celui oà chacun des
coefficients xk est nul.
est
celui oà chacun des
coefficients xk est nul.
Cette définition permet de distinguer clairement les deux caractÃres
essentiels dune base.
De mÃme que f bijective f surjective et f injective , on pourra énoncer :
S est une base du K-espace E S est générateur du K-espace E et S est K-libre.
Compléments et remarques sur la définition.
_ Lorsquil peut y avoir ambiguÃté au sujet du corps sur lequel est
construit lespace vectoriel on précisera systÃme K-libre.
Ainsi le systÃme S=(1, i) de
complexes est R-libre mais nest pas C-libre. En effet la combinaison linéaire x.1+y.i=0 entraine la nullité des
deux coefficients x et y lorsque ceux-ci sont supposés réels
mais peut Ãtre réalisée avec un jeu de complexes non nuls (ex : x=i ; y=-1)
Remarquons que tout systÃme C-libre
sera nécessairement R-libre.
_ Au lieu de libre on adopte aussi le terme de systÃme linéairement
indépendant.
_ Un systÃme non libre sera dit lié ou linéairement dépendant.
_ Un systÃme contenant le vecteur nul est toujours lié.
_ Un sous-systÃme dun systÃme libre est nécessairement libre,
une extension dun systÃme lié est toujours lié.
Formulations
particuliÃres : On tire immédiatement des définitions les
énoncés équivalents qui suivent :
a) Un systÃme S=(e1)
réduit à un seul vecteur est libre si et seulement si e1¹0E.
b) Un systÃme S=(e1,
e2) est libre aucun des deux vecteurs de S
nest multiple de lautre.
c) Si n ³3 un systÃme S=(e1, e2,
, en)
est libre
aucun des vecteurs de S ne peut sécrire comme combinaison linéaire des autres
vecteurs de ce systÃme.
Les deux premiÃres affirmations sont pratiquement évidentes à
justifier.
Pour la troisiÃme, de portée plus générale, procédons par contraposée.
_ Si S est lié, il existe un élément x
non nul de Kn tel que x1e1+
+xnen=0E.
Soit alors i un indice de tel que xi ¹0 (Il en existe car x nest pas, par hypothÃse, le jeu de coefficients
identiquement nul.)
On pourra donc écrire ![]() . Le vecteur ei est donc combinaison des
autres vecteurs de S.
. Le vecteur ei est donc combinaison des
autres vecteurs de S.
_ Si un des vecteurs de S, soit par exemple ei
,peut sobtenir comme combinaison linéaire des autres vecteurs de S : ![]() . On en déduit immédiatement par différence
. On en déduit immédiatement par différence ![]()
avec yk=xk pour
tout indice k distinct de i et yi=-1.
Le systÃme S est donc lié.
Sous cet angle, un systÃme lié dau moins 2 vecteurs apparait donc comme
un systÃme au sein duquel résident des éléments inutiles pour la tache de représentation en combinaisons
linéaires. En effet un vecteur combinaison linéaire des autres vecteurs du
systÃme sera superflu car tout multiple de celui ci pourra se décomposer
aussi comme combinaison linéaire de ces mÃmes vecteurs restants. (La
charge du multiple en question est répartie sur les autres).
On peut donc envisager des compressions de personnel dans un systÃme
lié en vue déliminer des éléments parasites et dobtenir un systÃme
minimal, libre, oà chacun des vecteurs sera essentiel au sein de cette
équipe S. Plus précisément :
Ce principe de compressions successives
est une des méthodes essentielles pour construire une base dun K-espace E non réduit à
pour lequel on connait un systÃme S=(e1,e2,
,en) générateur.
_ Si S est libre il constitue bien daprÃs ce qui précÃde une
base de E (générateur et libre ).
_ Si S nest pas libre, on enclenche le processus de compression que lon poursuit
jusquà obtenir un sous-systÃme S dans lequel aucun des vecteurs
nest combinaison des autres éléments de S ou bien est réduit à un seul
vecteur non nul.
S est donc libre et toujours générateur de E donc constitue une base de cet
espace, construite en quelque sorte comme un systÃme générateur minimal
obtenu en raffinant un systÃme générateur donné.
Il existe une autre façon tout aussi fondamentale de construire des bases dun
espace.(¹)
Son application repose sur la remarque suivante :
Si S=(e1 ,e2,
, en) est libre et si un vecteur en+1 nest pas combinaison linéaire des
vecteurs de S, alors lextension S du systÃme S obtenue en rajoutant le
vecteur en+1
est encore libre.
La preuve est simple : Supposons ![]() . On ne peut avoir xn+1 ¹0, sinon on en déduirait
immédiatement que en+1
est combinaison des vecteurs de S, ce qui est contraire à
lhypothÃse. Doà nécessairement xn+1=0.
. On ne peut avoir xn+1 ¹0, sinon on en déduirait
immédiatement que en+1
est combinaison des vecteurs de S, ce qui est contraire à
lhypothÃse. Doà nécessairement xn+1=0.
Il reste donc ![]() doà lon
déduit la nullité de tous les xk
pour kI puisque S est un systÃme supposé libre. Lextension S
est donc encore libre.
doà lon
déduit la nullité de tous les xk
pour kI puisque S est un systÃme supposé libre. Lextension S
est donc encore libre.
On peut là aussi donner une image économique de ce principe, en
considérant des embauches répétées
jusquà réalisation du projet dentreprise.
Ici le but à atteindre est la création dune équipe S permettant de
reconstituer tout vecteur de E comme combinaisons linéaires des éléments de S,
et ceci de maniÃre unique.
On commence par choisir arbitrairement un vecteur e1 non nul dans E.
_ Si tout vecteur de E est multiple de e1,
le systÃme S=(e1)
est alors générateur de E et libre puisque e1¹0E donc constitue une
base de E.
_ Sinon il existe au moins un vecteur de E non multiple de e1.
Soit e2 un de ces éléments
et S=(e1,e2). Létude précédente
montre que S est encore libre.
_ Si S est générateur de E, il constitue bien une base de cet espace. Sinon il
existe des vecteurs non combinaisons linéaires de S. On en recrute un, soit e3 , ce qui nous donne un
systÃme S=(e1, e2 , e3) toujours libre et couvrant un peu plus de vecteurs
par combinaisons linéaires que les systÃmes précédents.
Une différence essentielle avec la méthode descendante des compressions
successives est que lon nest pas sÃr ici darriver à terme fini
sur un systÃme effectivement générateur de E.
Ainsi dans le cas du K-espace des polynômes quelconques
à coefficients dans K il est clair
que le systÃme Sn=(1,X,
,Xn) est libre quelque soit
lentier n mais nest jamais
générateur de lespace total puisque ses combinaisons linéaires sont des
polynômes de degré au plus n.
En résumé nous disposons de deux méthodes générales, lune descendante,
lautre ascendente, pour construire des bases dun K-espace E mais avec les limitations suivantes :
_ Pour démarrer la premiÃre il faut disposer dun systÃme S=(e1,
e2,
,en) générateur.de E.
_ On nest pas sÃr que la deuxiÃme aboutisse au bout dun nombre
fini détapes.
A la question de comment construire des bases sajoute aussi une
interrogation naturelle :
toutes les bases que lon va ainsi construire au sein dun mÃme espace E
auront elles toujours le mÃme nombre de vecteurs ?
La recherche démarrée ici va séclaircir trÃs nettement dans le
paragraphe suivant à la lumiÃre dun théorÃme essentiel
aux nombreuses retombées que nous appellerons le théorÃme fondamental de
la dimension.
2)
ESPACES DE DIMENSION FINIE.
A)
ThéorÃme fondamental
Pour tout entier n non nul, n+1 vecteurs dun K-espace E tous combinaisons linéaires dun mÃme systÃme S de n vecteurs de E sont toujours en situation de dépendance linéaire.
Nous allons procéder par récurrence sur lentier n.
1) Pour n=1. Soit S=(e1) un systÃme réduit
à un seul vecteur de E et S=(u1,
u2) formé de deux vecteurs
multiples de e1, cest
à dire du type u1=ae1 ; u2=be1.
On en déduit immédiatement la relation bu1-au2=0E qui assure
le caractÃre lié du systÃme S lorsque le couple (a, b)
nest pas identiquement nul.
Si (a, b)=(0,0). Il est encore plus évident que S est lié puisquil
contient le vecteur nul.
2) Pour n=2. Notons  3 combinaisons de S.
3 combinaisons de S.
_ Supposons y¹0. On peut alors écrire ![]() puis en déduire, en
substituant dans les deux premiÃres égalités, le systÃme :
puis en déduire, en
substituant dans les deux premiÃres égalités, le systÃme : 
Remarquons alors que les vecteurs ![]() forment un
systÃme lié daprÃs létude précédente car ils sont tous deux
multiples de e1. Il existe
donc une combinaison linéaire de ces vecteurs utilisant un couple de
coefficients (a b) non identiquement nul et
conduisant au vecteur nul de E.
forment un
systÃme lié daprÃs létude précédente car ils sont tous deux
multiples de e1. Il existe
donc une combinaison linéaire de ces vecteurs utilisant un couple de
coefficients (a b) non identiquement nul et
conduisant au vecteur nul de E.
AprÃs regroupement des termes cela peut sécrire : 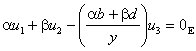
Ceci montre clairement que le systÃme S est lié puisque (a b ¹(0,0).
_ Si y=0. Il est clair que la notion
de liberté ne dépend pas de lordre des vecteurs dun systÃme. On pourra
donc si b¹0 échanger u1 et u3 ce
qui nous ramÃne à la situation précédente avec encore la
conclusion S lié. De mÃme si b=0
mais d¹0 on échangera u2 et u3.
Reste le pire des cas oà y=b=d=0.
Mais dans cet état les trois vecteurs de S sont multiples du seul vecteur e1. S est alors lié puisque
extension du systÃme (u1,
u2) lui mÃme lié
daprÃs létude faite pour n=1.
3) Plus généralement, supposons la propriété établie pour un certain entier n ³2.
Le passage au rang suivant n+1 va
seffectuer suivant le mÃme principe que le passage de 1 à 2
examiné ci dessus. La seule difficulté réside dans lécriture à double
indice, nécessaire ici pour représenter une configuration générale.
On posera donc S=(e1, e2,
., en, en+1) et S=(u1,
u2,
.., un+1, un+2) avec pour
tout indice i de : ![]()
_ Si le dernier coefficient y=a(n+2,n+1) du dernier vecteur un+2 est non nul on pourra écrire
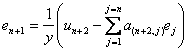 , puis en substituant cette expression dans les n+1 premiÃres égalités, en
déduire le systÃme formé par les égalités du type :
, puis en substituant cette expression dans les n+1 premiÃres égalités, en
déduire le systÃme formé par les égalités du type :
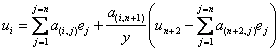 , pour i variant de 1 à n+1.
, pour i variant de 1 à n+1.
Les n+1 vecteurs vi=![]() sont alors tous combinaisons linéaires du mÃme
systÃme Sr formé
par les n premiers vecteurs ej ; jI.
sont alors tous combinaisons linéaires du mÃme
systÃme Sr formé
par les n premiers vecteurs ej ; jI.
DaprÃs lhypothÃse de récurrence à lordre n ils forment donc un systÃme lié
et on pourra trouver un (n+1)-uplet
non identiquement nul, soit (x1,
..,
xn+1) tel que x1v1+
..+xn+1vn+1=0E.
En développant puis en regroupant les multiples de un+2 on obtient la relation :
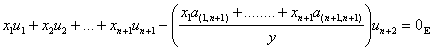 qui assure la
dépendance linéaire de S puisque un au moins des n+1 premiers coefficients est non nul.
qui assure la
dépendance linéaire de S puisque un au moins des n+1 premiers coefficients est non nul.
_ Si y=a(n+2, n+1)=0 mais
quun au moins des coefficients de la derniÃre colonne est non nul,
par exemple si a(k,n+1)
est différent de zéro, on échangera uk
et un+2 ce qui
nous ramÃnera à la situation précédente et donc encore à
la dépendance linéaire de S.
Enfin, si tous les coefficients de la derniÃre colonne sont nuls, les
vecteurs de S sont tous combinaisons linéaires du systÃme réduit formé
des n premiers vecteurs Sr=(e1,
., en).
DaprÃs lhypothÃse de récurrence au rang n S est donc encore lié en
tant quextension dun systÃme de n+1
vecteurs tous combinaisons linéaires du systÃme de n vecteurs Sr.
B) Applications.
Une
premiÃre conséquence importante est quau sein dun espace E possédant
un systÃme générateur fini S de n
vecteurs, la méthode de recherche dune base par extensions successives dun
systÃme libre initial conduira toujours à une solution effective.
En effet on sait
maintenant que n est un plafond pour
le nombre de vecteurs dun systÃme libre de E, ceci daprÃs le
théorÃme fondamental. (n+1
vecteurs tous combinaisons linéaires du mÃme systÃme S à n vecteurs forment un systÃme
lié.).
On ne pourra donc étendre indéfiniment un systÃme en gardant son
caractÃre libre. Au bout dun nombre fini détapes dans la méthode de
recherche ascendante on mettra en évidence un systÃme libre maximal,
donc nécessairement générateur de lespace total E.
Dans
la foulée considérons deux bases du mÃme espace E, lune notée B formée de n vecteurs, lautre désignée par B de cardinal p.
B étant génératrice et B libre, le théorÃme fondamental
implique p £ n.
En inversant les rôles, chaque base étant à la fois libre et
génératrice, on en déduit n £p. Ainsi au sein dun mÃme espace toutes les bases ont
nécessairement le mÃme nombre déléments.
Ceci nous permet de poser les définitions suivantes :
_ On dira quun espace est de dimension
finie si et seulement si il possÃde un systÃme générateur
fini.
_ Si E est un espace de dimension finie non réduit au seul vecteur nul, E
possÃde des bases et toutes ces bases ont nécessairement le mÃme
nombre déléments que nous appellerons la dimension du K-espace E et qui sera noté dimK(E).
Remarque : Lespace trivial est bien de dimension
finie car le systÃme S réduit à 0E est générateur,
mais ne possÃde pas de base puisque S nest pas libre.
Par convention nous poserons dimK=0. (Ne pas chercher
dans E des bases à 0 éléments ! Il sagit simplement dun artifice
qui évitera de considérer des cas particuliers dans les résultats essentiels de
la théorie de la dimension énoncés ci-aprÃs.)
_ Enfin nous dirons aussi quun espace est de dimension infinie sil nest pas
de dimension finie.
Si E est un espace de dimension
non nulle n.
_ Tout systÃme générateur de E de cardinal n est une base de E.
_ Tout systÃme libre de E de cardinal n est une base de E.
En effet, soit pour commencer un systÃme S engendrant E formé de n vecteurs.
_ Si S est réduit à un seul vecteur, celui ci ne peut Ãtre nul,
sinon lespace engendré E serait réduit à ce qui est
contraire à lhypothÃse n¹0.
_ Si n >1 et si S nétait pas libre, on
pourrait alors compresser S à un systÃme de n-1 vecteurs engendrant encore E. Or ceci est en contradiction avec
le théorÃme fondamental car E est de dimension n donc possÃde des systÃmes libres de n vecteurs .
S générateur de E est donc aussi libre et constitue bien ainsi une base de E.
Considérons maintenant un systÃme libre L de cardinal n.
Si L nengendrait pas E, on pourrait alors létendre en un systÃme libre
L de n+1 vecteurs, en rajoutant un
élément de E non combinaison linéaire de L.
Ceci est directement en contradiction avec le théorÃme fondamental, le
cardinal dun systÃme générateur de E étant un plafond pour le nombre de
vecteurs dun systÃme libre de E. ( On aurait n+1£n). L est donc libre et générateur de E.
On a en fait repris lidée essentielle des méthodes ascendantes et descendantes
dans lesquelles une base apparait soit comme un systÃme libre maximal,
soit comme un systÃme générateur minimal. Résumons létude par les
équivalences suivantes :
Si card(S)=dimK(E) S base de E
S libre dans E
S générateur de E.
Si E est de dimension finie n, tout sous-espace A de E est
nécessairement de dimension finie p
inférieur ou égal à n. De plus
si p=n ce sous-espace A coÃncide avec lespace
total E.
_ Si A=, le résultat est évident et tient à la convention
adoptée plus haut.
_ Si A¹
enclenchons la méthode ascendante de recherche dune base de A par extensions
successives dun systÃme libre initial L. (Par exemple en partant de L= avec v quelconque non nul dans A).
E étant de dimension finie n, le cardinal
dun systÃme libre de vecteurs de E (et donc aussi dun systÃme
de vecteurs du sous-espace A) sera majoré par n. Au bout dun nombre fini détapes on est alors sÃr
datteindre un systÃme libre maximal B dans A soit une base de A formé dun
nombre p de vecteurs avec p£n . A est bien de dimension finie p.
Enfin, si p=n, la base B de A construite ci dessus apparait comme
un systÃme libre maximal de E, donc une base de cet espace total. E est
alors formé par lensemble des combinaisons linéaires dun systÃme de
vecteurs de A et est donc inclus dans A vu la stabilité dun sous-espace pour
les combinaisons linéaires. On a bien établi E=A.
Si
A et B sont deux sous-espaces de dimension finie dun mÃme K-espace E, alors A B et A+B sont aussi de dimension
finie et satisfont à léquation aux dimensions suivante :
dimK(A+B)=dimK(A)+dimK(B)-dimK(A B)
En particulier, si la somme est
directe : dimK(AÅB)=dimK(A)+dimK(B)
_ Remarquons dabord que si un des sous espaces A ou B est réduit à ,
le résultat sera évident vu la convention dimK=0.
_Examinons ensuite le cas le cas dune somme directe. Par hypothÃse on
peut construire une base B=(e1,
., en)
de A et une base B=(u1,
, up)
de B.
Or par définition tout vecteur v de
A+B peut sécrire comme somme dun vecteur de A avec un vecteur de B donc peut
se décomposer, en utilisant le caractÃre générateur de B et B, sous la forme : v=x1e1+
.+xnen+y1u1+
.+ypup .
Le systÃme B obtenu en juxtaposant B et B
apparait donc comme engendrant le sous-espace somme A+B. Montrons que B est libre.
Considérons pour cela un jeu de coefficients de K, soit : (x1,
.,xn, y1,
., yp), tel que x1e1+
.+xnen+y1u1+
.+ypup = 0E. La somme étant supposée
directe, chacune des deux composantes sur A et B est nulle , cest à
dire x1e1+
.+xnen= y1u1+
.+ypup = 0E
On termine en utilisant le caractÃre libre de B et B. Nécessairement, chacun des coefficients
xi et yj
apparaissant dans les deux combinaisons nulles suivantes est nécessairement
égal à 0.
On a donc bien mis en évidence un systÃme générateur et libre de A+B
donc une base B de cardinal n+p=dimK(A)+dimK(B).
Retenons au passage le principe de construction par juxtaposition dune base
de A avec une base de B.
_ Abordons pour finir le cas général oà A B¹ et choisissons
comme point de départ une base B=(e1,
., er)
de cette intersection.
_ Si A B=A
ou A B=B, le résultat cherché est
encore évident car lun des deux sous-espaces sera inclus dans lautre, et la
somme ne sera autre que le plus grand des deux.
_ Sinon, on pourra en utilisant la méthode ascendante, compléter dune part B en une base B de A en rajoutant judicieusement des
vecteurs u1,
,up , dautre part prolonger
ce mÃme systÃme B en une base B de B en rajoutant v1,
.,vq
.
Tout vecteur a de A peut alors sécrire
comme combinaison linéaire du type :
a=x1e1+
+xrer+y1u1+
.+ypup
De mÃme tout vecteur b de B
peut sobtenir sous la forme :
![]()
On en déduit que tout vecteur de la somme A+B pourra se décomposer suivant le
format :
![]()
Le systÃme B=(e1,
.,er,,u1,
,up,v1,
.,vq) apparait donc comme
générateur de A+B.
Montrons quil est libre et considérons pour cela une combinaison du
type :
x1e1+
+xrer+y1u1+
.+ypup
+z1v1+
.+zqvq=0E.
On en déduit immédiatement légalité :
x1e1+
+xrer+y1u1+
.+ypup=-( z1v1+
.+zqvq) dans laquelle le premier membre est un
vecteur de A et le second un élément de B.
Il sagit donc dun vecteur de lintersection que lon va pouvoir décomposer
dans la base B , doà une nouvelle
égalité du type :
x1e1+
+xrer+y1u1+
.+ypup=-( z1v1+
.+zqvq)=t1e1+
.+trer
Or B étant une base on aura nécessairement,
vu lunicité de la décomposition, les égalités
x1=t1 ;
.. ; xr=tr ;
y1=0 ;
. ; yp=0.
De mÃme B étant une base on en conclÃt t1=0 ;
. ; tr=0 ; z1=0 ;
. ; zq=0.
Tous les coefficients de la combinaison étudiée sont donc nécessairement nuls. B est bien une base de la somme A+B dont
la dimension est r+p+q=(r+p)+(r+q)-r cest à
dire effectivement dimK(A)+dimK(B)-dimK(A B)
C) Quelques Résultats classiques.
1) Dimension des espaces standards.
Pour les
espaces vectoriels classiques, la mise en évidence de bases simples dites
naturelles ou canoniques donne directement la dimension.
_ Ainsi K est un K espace de dimension 1, en considérant la base évidente réduite
à 1K.
_ Lespace produit Kn est de dimension n sur K, en considérant la base élémentaire
formée des n-uplets ek dont toutes les
composantes sont nulles sauf celle d'ordre k
égale à 1K.
e1=(1K, 0K,
.,0K) ; e2=(0K,
1K, 0K,
, 0K) ;
; en=(0K,
.. , 0K, 1K).
_ Lespace Kn[X] est de dimension n+1 sur K, en remarquant que le systÃme de fonctions monômes Sn=(1, X, X²,
., Xn) est bien libre et
générateur de cet espace.
_ Lespace K[X] nest pas de dimension finie
sur K puisque le systÃme Sn défini ci dessus est libre
quel que soit lentier n.
2) C
espaces et R
espaces.
Soit E est un C-espace de dimension finie n, et B=(e1,e2,
.,en) une base de E.
Pour tout vecteur v de E il va
exister un unique jeu de complexes (z1,
..,
zn) tel que v se décompose v=z1e1+
+znen. En écrivant
les zk sous forme
algébrique zk=xk+iyk
, cette égalité se traduit vu les axiomes dun C-espace : v=x1e1+
.+xnen+y1(ie1)+
..+yn(ien).
Le systÃme S=(e1, e2,
.,en, ie1,
ie2,
., ien) apparait alors comme un
systÃme générateur du R espace E. Il est facile de
prouver que ce systÃme est libre. En effet une combinaison linéaire
à coefficients réels du type x1e1+
.+xnen+y1(ie1)+
..+yn(ien)=0E se
condense avec les notations précédentes en la combinaison à coefficients
complexes z1e1+
+znen=0E et entraine donc la
nullité de chacun des complexes zk=xk+iyk
par suite du caractÃre C-libre de B et par suite la nullité de tous les
couples de réels (xk, yk).
S est donc une R-base de E et on peut donc écrire
que dimR(E)=2n=2dimC (E)
La dimension de E en tant que R-espace est le double de sa
dimension sur C.
3) Dimension dun espace produit.
Soit B =(e1,
.,en)
une base dun K-espace E et B=(u1,
,up)
une base du K-espace F.
Si on munit le produit cartésien P=E F des lois classiques :
(x,y)+(x,y)=(x+x,y+y) et a.(x,y)=(ax ay) pour a scalaire, il est clair que lon
construit un K-espace vectoriel et que le
systÃme de n+p couples (e1, 0F),
..,( en, 0F), (0E, u1),
..,(0E, up) en est une base. Il suffit décrire (x,y)=(x,0F)+(0E,y) puis de décomposer les vecteurs x et y
dans les bases respectives B et B. On aura donc dimK(E F)=dimK(E)+dimK(F).
La formule se généralise sans problÃme à un produit dun nombre
fini de K-espaces :
dimK(E1 E2 En)=dimK(E1)+dimK(E2)+
..+dimK(En)
3) DIMENSION ET MORPHISMES DESPACES.
Dans ce paragraphe E et F désignent deux espaces vectoriels
sur le mÃme corps K, reliés par une application K-linéaire f de E vers F. On se propose détudier comment le morphisme f agit sur les caractÃres liés
à la notion de dimension.
Commençons par établir les résultats élémentaires suivants :
Soit S=(e1, e2,
., en) un systÃme fini de vecteurs de E et f(S)=(f(e1),
.., f(en))
le systÃme dit image de S par f
, formé par les images successives des éléments de S.
1) Si S est générateur de E, alors le
systÃme f(S) est générateur de f(E).
2) Si S
est libre, alors f(S) est libre si et seulement si VecK(S)
Ker(f)=.
_ Pour la premiÃre propriété remarquons que par définition mÃme,
tout vecteur w de f(E) est du type w= f(v) avec v élément de E.
S engendrant E, on pourra écrire v
comme combinaison linéaire des vecteurs de S : v=x1e1+
.+xnen . Enfin, par K-linéarité de f, on obtient : w=x1f(e1)+
..+xnf(en) .
Le systÃme f(S) est donc bien générateur de f(E).
_ Pour la deuxiÃme affirmation supposons S libre et examinons une
combinaison linéaire du systÃme f(S)
donnant le vecteur nul : x1f(e1)+
..+xnf(en)=0F.
Toujours par K-linéarité de f on en déduit f(x1e1+
.+xnen)=0F
, exprimant lappartenance au noyau de f
du vecteur v= x1e1+
.+xnen .
Or v appartient au sous-espace
vectoriel engendré par S, noté classiquement VecK(S).
a Si ce sous espace ninterfÃre
avec le noyau que par le vecteur nul, on aura donc nécessairement v=0E, et par suite chacun des
coefficients xk nul vu que
S est supposé libre.
a Par contre si il existe un
vecteur non nul appartenant à la fois à VecK(S) et
à Ker(f), on pourra lécrire v=x1e1+
.+xnen
avec la relation x1f(e1)+
..+xnf(en)=0F.
Or au moins un des coefficients xk
est non nul puisque v¹0E. On a donc ici une
relation de dépendance linéaire entre les vecteurs de f(S). Par contraposée on en déduit que si S est libre, alors VecK(S) Ker(f)=.
Ces deux principes de base établis examinons les premiÃres conséquences
suivantes :
Limage par f dun sous-espace A de dimension finie n est un sous-espace de dimension finie tel que dimK( f(A)) £
dimK(A).
Il suffit dappliquer la premiÃre propriété à la restriction de f au sous-espace A.
Si S est une base du K-espace A formée de n vecteurs, le systÃme f(S) sera un systÃme de n vecteurs générateur de lespace image f(A). Par suite f(A) est bien de dimension finie p£n
Si f est injective, limage dun systÃme libre par f est toujours un systÃme libre.
En effet Ker(f) étant réduit à ,
la deuxiÃme propriété nous donne directement le résultat.
Si A est un sous-espace de
dimension finie, dimKf(A)=dimK(A)-dimK(A Ker(f))
a Si A Ker(f)= il suffit dappliquer les deux résultats
précédents. En effet limage par f
dune base de A sera à la fois libre et génératrice de f(A) donc une base de cet espace image
constituée dun nombre de vecteurs égal à la dimension de A.
Dans ce cas f conserve la dimension.
a Si dimK(A Ker(f))=p avec p³1. (Cette dimension est bien finie
puisque la trace de A sur le noyau de f
est un sous-espace de A de dimension finie.)
Partons alors dune base S=(e1,
e2,
., ep) de cette intersection et
étendons la en une base B =(e1, e2,
.,
en) de A. On sait que f(B) est un systÃme générateur de f(A).
Cependant, dans ce systÃme, les images f(ek) des p premiers
vecteurs sont nulles puisquil sagit dimages par f de vecteurs du noyau de f.
On peut donc compresser ce systÃme générateur en éliminant ces images
inutiles.
_ Si p=n on a alors A Ker(f)=A donc AÌKer(f)
et f(A)=.
_ Si p<n le systÃme réduit apparait comme limage dun systÃme S=(ep+1,
., en) tel que VecK(S) Ker(f)=. En effet la juxtaposition de S et S étant une
base de A on a vu un peu plus haut que VecK(S)ÅVecK(S)=A.
Le deuxiÃme principe nous assure alors que f(S) est libre. On a donc
construit une base de f(A) formée de n-p vecteurs.
Dans les deux cas on a bien dimKf(A)=n-p=dimK(A)-dimK(A Ker(f)).
Cette relation précise le rôle important du noyau pour la connaissance dun
morphisme f.
Si E est de dimension finie,
alors dimK( f(E))=dimK(E) dimK(Ker(f))
Il suffit
dappliquer le résultat précédent à A=E.
Ce théorÃme est souvent connu comme le théorÃme du rang car il permet de préciser ce que lon appelle
le rang dune application linéaire,
cest à dire la dimension de lespace image :.Im(f)=
f(E).
Si E est de dimension finie et si
f est bijective, alors dimK(F)=dimK(E)
Cest un cas particulier du résultat précédent avec A=E puisque f(E)=F et Ker(f)=
Deux espaces de dimension finie isomorphes sont donc nécessairement de mÃme
dimension.
Un espace de dimension finie ne peut Ãtre isomorphe à un espace de
dimension infinie.
Si E et F sont deux K
espaces de mÃme dimension finie, alors pour tout application linéaire f de E vers F : f bijective
f injective
f surjective .
_ On sait que f est injective si et
seulement si Ker(f) est réduit
à . Ceci équivaut daprÃs le théorÃme du
rang à : dimK( f(E))=dimK(E), donc daprÃs
lhypothÃse, à légalité
dimK( f(E))=dimK(F),
ou encore à f(E)=F puisque f(E) est un sous-espace de
F.
Ainsi linjectivité de f équivaut
à sa surjectivité et par suite à sa bijectivité.
En particulier, pour montrer quun
endomorphisme f dun K-espace
E de dimension finie est bijectif il suffira détablir un seul des deux
caractÃres fondant cette notion, linjectivité ou la surjectivité.
De mÃme pour vérifier que lendomorphisme g est réciproque de f, il
suffira de sassurer quune au moins des deux égalités g![]() f=IE ou f
f=IE ou f![]() g=IE est
réalisée.
g=IE est
réalisée.
En effet de la premiÃre on déduit directement linjectivité de f ainsi que la surjectivité de g. Létude ci dessus assure alors la
bijectivité de g et f et la relation g=f 1.
Raisonnement identique à partir de la deuxiÃme égalité en
échangeant les rôles des deux applications.
Deux K-espaces
de mÃme dimension finie sont nécessairement isomorphes.
Pour létablir
il suffit de remarquer que tout K-espace de dimension finie n est isomorphe à lespace
standard Kn par lintermédiaire de
lapplication j
définie aprÃs le choix dune base B=(e1,e2,
.,en).de
E comme :
v=x1e1+
.+xnen
, j(v)=(x1,
.,
xn).
Il ne sagit pas vraiment ici dune application des deux principes en question
mais simplement une autre formulation de la notion de base, déjà évoquée
dans le premier paragraphe.
4) RANG DUN SYSTEME.
On a défini précédemment le rang dune application linéaire
comme la dimension de son espace image.
Plus généralement nous appellerons rang
dun systÃme S de vecteurs du
K-espace E la dimension du K-espace engendré par S.a rang(S)=dimK(VecK(S))
Le lien entre les deux notions est précisé par la propriété évidente qui
suit :
Si fILK(E,F) et si S=(e1,e2,
.,en) est une base de E, alors rang(f)=rang(f(e1),f(e2),
.,f(en))
.
En effet on sait que si S est générateur de E, f(S) engendre f(E)=Im(f).
Détermination pratique du rang.
On peut toujours bien sÃr appliquer la méthode consistant à
compresser progressivement le systÃme générateur initial S
jusquà obtention dune base. Cependant la détermination effective de
relations de dépendance linéaire nest pas toujours évidente si le nombre de
vecteurs de S est élevé.
On lui préfÃre souvent une méthode plus algorithmique décrite
ci-aprÃs, reposant sur un principe dit du pivot de Gauss, assez
universelle puisquon la retrouvera dans la résolution des systÃmes
linéaires et le calcul des déterminants, avec lavantage considérable de
pouvoir se transcrire aisément dans les langages de programmation usuels.
Description de la méthode.
A) Notation matricielle.
La mise en place nécessite la connaissance des composantes des vecteurs de S
dans une base du K-espace détude E.
Nous désignerons par B=(e1, e2,
.,
en) une telle base et
noterons S=(u1,
.., up) avec pour tout k élément de : ![]() =
=![]()
La notation a double indice est ici inévitable. Notons quelle fait apparaitre
une application x définie sur le
produit cartésien à valeurs dans K
avec pour ![]() la composante suivant ei dans la base B du vecteur uk.
la composante suivant ei dans la base B du vecteur uk.
Cette application sera souvent résumée à laide dun tableau à
double entrée constitué de n lignes
et p colonnes et dont lélément
générique situé à la croisée de la ligne i et de la colonne k sera
précisément ![]() . Ce tableau sera appelé matrice des composantes des vecteurs
du systÃme S dans la base B (ou plus simplement matrice de S
dans B ).
. Ce tableau sera appelé matrice des composantes des vecteurs
du systÃme S dans la base B (ou plus simplement matrice de S
dans B ).
Sa colonne dordre k notée Ck représente dans lordre les
composantes de uk dans la
base B .
Mat(S,B )=A=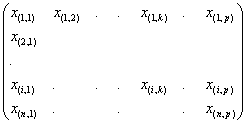
B) Rang dun systÃme
triangulaire inférieur.
On appelle ainsi, de maniÃre imagée, un systÃme S de r vecteurs dont la matrice
représentative dans B ne contient que des zéros dans le triangle correspondant aux couples
(i,
k) dindices tels que i < k. Ces vecteurs se décomposent donc suivant le schéma :
![]()
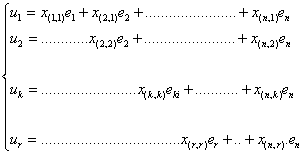
Il sagit en fait plutôt dun dessin en trapÃze, le vrai triangle
napparaissant que si r=n.
LintérÃt de cette structure réside dans la propriété qui suit :
Si aucun des coefficients diagonaux x(i,i) nest nul, alors le rang du
systÃme est égal à r.
La preuve est facile. Considérons une relation de dépendance a1u1+
..+arur=0E.
Chacune des composantes dans la base B
de la combinaison linéaire précédente doit donc sannuler.
_ Ainsi, en projetant sur e1.,
on obtient a1x(1,1)=0 doà lon tire a1=0 puisque x(1,1)
¹0.
_ Ensuite, en projetant sur e2
on aura a1x(2,1)+a2x(2,2)=0.
Mais a1=0 et x(2,2)
nest pas nul, on en déduit donc a2=0.
_ Il est facile de poursuivre ce procédé en cascade et de montrer que de proche
en proche tous les coefficients ak
vont sannuler successivement jusquà ar. Le systÃme étudié est donc bien libre, son
rang est égal à son cardinal r..
C) Manipulations conservant le rang
dun systÃme.
La partie active de la méthode va consister à laide de
transformations élémentaires, à remplacer le systÃme initial S en
un systÃme triangulaire du type précédent, sans modifier lespace
vectoriel engendré.
Pour cet objectif trois types de manipulations fondamentales suffisent, que
lon va codifier de la façon suivante :
a) ![]() Echange des
vecteurs uk et uj.
Echange des
vecteurs uk et uj.
b) ![]() Remplacement du
vecteur uk par le multiple
auk avec a non nul.
Remplacement du
vecteur uk par le multiple
auk avec a non nul.
c) ![]() . Remplacement du
vecteur uk par la
différence uk-uj avec k
¹j .
. Remplacement du
vecteur uk par la
différence uk-uj avec k
¹j .
Justifications :
_ La somme des vecteurs étant commutative, la modification de lordre des
vecteurs dun systÃme S ne perturbe aucunement lespace vectoriel
engendré par celui-ci. La premiÃre transformation est donc tout à
fait licite.
_ Si le scalaire a est non nul, les
droites vectorielles engendrées par uk
et auk sont identiques et
ces deux vecteurs ont donc des rôles interchangeables pour ce qui concerne les
combinaisons linéaires. Ceci justifie lemploi de la manipulation b).
_ Enfin remarquons que le sous-espace engendré par le couple (uk,uj) est identique à celui engendré par (uk-uj,,uj).
Il suffit de remarquer que uk=(uk-uj)+uj.
On pourra donc aussi utiliser des manipulations du type c).
Ces justifications précisées, le déroulement des opérations est relativement
simple :
_ En modifiant au besoin lordre, on se place sous lhypothÃse oÃ
la premiÃre composante
a=x(1,1) du premier
vecteur u1 est non
nulle.(Si toutes les composantes sur e1
sont nulles, on travaillera sur la base restreinte B ,
suffisante pour représenter les vecteurs de S)
_ On remplace ensuite pour chaque k >1 chacun des vecteurs uk
par ![]() .
.
Ceci ne modifie rien si x(1,k) est nul, et correspond dans le
cas contraire à lenchainement des trois opérations permises : 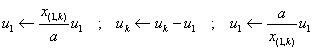
Cette séquence a pour effet de mettre à zéro toutes les composantes
suivant e1 des vecteurs uk dindice k
strictement supérieur à 1. Notons S1 le sous systÃme
formé par ces r-1 vecteurs ainsi
modifiés.
_ On recommence avec S1 la démarche précédente avec cette fois ci
lobjectif dannuler les composantes sur e2 (sauf une !).
_ On poursuit le procédé jusquà obtention de la forme triangulaire
recherchée.
Si au cours de ces opérations le vecteur nul apparait, il sera bien entendu
exclu du systÃme en évolution car il na aucune influence sur le rang.
Insistons sur la forme dépouillée de la méthode : on nutilise que les
composantes des vecteurs de S dans la base B . On travaille en fait dans lespace
standard Kn, isomorphe à E par
lintermédiaire de la base B suivant : v=x1e1+
+xnen
a(x1,
, xn).
Le rang de S est donc aussi celui du systÃme S des vecteurs colonnes de
la matrice représentant S dans B , rang que lon appellera donc
aussi rang de la matrice A= Mat(S,B )
Lintervention de cette matrice a un autre intérÃt pratique non
négligeable. On va montrer en effet que le rang de A, cest à dire du
systÃme des vecteurs colonnes coÃncide en fait aussi avec le rang
du systÃme des vecteurs lignes de cette matrice, considérés comme
vecteurs de lespace standard Kp.
Cette symétrie nétait pas du tout imaginable à priori, en restant
prisonnier de lespace initial E oà sont choisis les vecteurs de S. La
détermination pratique du rang pourra donc Ãtre enrichie de manipulations
du type pivot de Gauss sur les lignes de la matrice et conduire plus rapidement
au résultat.
Reste donc à justifier cette égalité des rangs des systÃmes
lignes et colonnes dune mÃme matrice rectangulaire. Cest encore une
conséquence simple du théorÃme fondamental de la dimension, avec pour seule
difficulté une notation indicielle un peu lourde et obscure.
Aussi pour montrer comment intervient le principe essentiel et alléger
lécriture nous allons dabord considérer le cas particulier oà le rang
du systÃme des vecteurs colonnes est égal à 3 et oà les
trois premiÃres colonnes forment effectivement un systÃme libre.
On aura ainsi pour tout k supérieur
ou égal à 3 : Ck=akC1+bkC2+gkC3.
Examinons alors une ligne quelconque de A, soit Li.
Ses trois premiers termes sont les coefficients respectifs 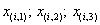 des colonnes
respectives C1, C2, C3, et le coefficient
dordre k ³4 sécrit
des colonnes
respectives C1, C2, C3, et le coefficient
dordre k ³4 sécrit ![]() .
.
Considérons alors les trois lignes l1, l2, l3
définies comme suit :
l1=(1, 0, 0, a ak ap)
l2=(0, 1, 0, b bk bp)
l3=(0, 0, 1, g gk , gp)
Il est clair que Li=x(i,1)l1+x(i,2)l2+x(i,3)l3. Lespace des vecteurs lignes
possÃde donc un systÃme générateur formé de 3 vecteurs et par
suite sera de dimension inférieure ou égal à 3.
On généralise sans peine ce raisonnement si le rang du systÃme des
vecteurs colonnes est quelconque. On établit donc ainsi que : rang(L1,
.,Ln)
£ rang(C1,
.,Cp).
Une démarche symétrique peut seffectuer en échangeant dans la précédente les
rôles joués par les lignes et les colonnes.
On en déduit linégalité inverse et par suite légalité des deux rangs.
Soit
E un R-espace vectoriel,![]() et
et ![]() deux vecteurs de E et
S le systÃme défini par les trois vecteurs
deux vecteurs de E et
S le systÃme défini par les trois vecteurs ![]() .
.
Montrer que S est lié et donner une relation de dépendance linéaire précise
entre ses vecteurs.
Dans
le R-espace des fonctions de R dans R on considÃre f1,
f2, f3 définies par
les formules :
f1(x)=sin(x+1) ; f2(x)=sin(x-1) ; f3(x)=sin(x+2).
a) Le systÃme S formé par ces trois fonctions est-il libre ?
b) Déterminer une base de E=VecR(S).
c) Déterminer les composantes de la fonction x asin(x)
dans la base précédente.
Soit
S=(e1, e2,
., en) un systÃme libre dun C espace E.
Le systÃme S=(e1+e2, e2+e3,
..,
en-1+en, en+e1)
est-il également libre ?
Dans
R on considÃre lensemble E des
quadruplets (x, y, z, t) tels
que :
2x+y+t=0 et x+y-z+3t=0
Montrer que E est un sous-espace et déterminer en une base.
Soit S le R-espace des suites à valeurs réelles. On note E lensemble des éléments de S tels que les termes de rang pair soient en progression arithmétique ainsi que les termes de rang impair. Montrer que E est un sous-espace de S de dimension finie.
Dans
R on considÃre le sous-ensemble E
des triplets du type (x+y-3z, x+2y-t,
t+x-z) , les coefficients x,
y, z, t pouvant prendre toute valeur réelle.
Montrer que E est un sous-espace de dimension finie et déterminer en une base.
Dans
le R-espace des fonctions de R dans R montrer que le systÃme de n vecteurs définis par les formules : sin(x), sin(2x),
., sin(nx) ,
est libre quel que soit lentier n
non nul.
(On pourra procéder par récurrence et mettre à profit loutil de la
dérivation.)
Ceci prouvé, la fonction ![]() appartient-elle au
sous-espace engendré par le systÃme défini ci dessus ?
appartient-elle au
sous-espace engendré par le systÃme défini ci dessus ?
Soit
E un R-espace de dimension 4 décomposé
sous la forme E=VecR(a,b)ÅVecR(c,d).
Peut on en déduire E=VecR(a+c)ÅVecR(b,
d, c-a) ?
Que se passe t-il si on supprime lhypothÃse sur la dimension de
E ?
Dans
le R-espace des fonctions de R dans R on considÃre pour tout entier non nul k le vecteur fk défini par la formule fk(x)=ln(x²+k).
Le systÃme Sn=(f1, f2,
, fn)
est il libre pour tout n entier non
nul ?
Dans R on considÃre le systÃme S
formé des 4 vecteurs :
e1=(2, 0, 1) ; e2=(-1, 1, 1) ; e3=(3, 1, 3) ; e4=(3, -1, 0). Déterminer le
rang de S, donner une base de R3 qui soit extension dune base du
sous-espace engendré par S.
Montrer que tout systÃme S=(P1, P2, ., Pn) de polynômes non nuls à coefficients dans K dont les degrés sont tous distincts deux à deux est nécessairement libre.
On considÃre lensemble
noté M3(R) des matrices carrés à
coefficients réels dordre 3
(3 lignes et 3 colonnes) muni des lois usuelles suivantes :
_ Somme + des matrices, définie en additionnant terme à terme les
éléments correspondants de chacun des tableaux.
_ Produit . dune matrice par un réel a, obtenu en multipliant chacun des
éléments du tableau par le scalaire a.
1) Montrer que (M3(R) , +, . ) est un R-espace vectoriel de dimension finie.
2) On note E lensemble des carrés magiques dordre 3, cest à dire des
éléments de M3(R) pour lesquels les sommes des 3
colonnes, des 3 lignes et des deux diagonales sont toutes égales entre elles.
Déterminer une base de E.
Soit E un R espace de dimension infinie, F et P deux sous-espaces de E tels que E=FÅP avec dimR(P)=2. Montrer que tout autre sous-espace G supplémentaire de F dans E cest à dire tel que E=FÅG est nécessairement de dimension 2.
Dans R [X] quel est le rang du systÃme
constitué par les 5 polynômes :
P1=1+2X-X²+X3 ; P2= 2+7X+2X3 ;
P3=5+X-11X²+5X3 ; P4=-1+X+3X²-X3 ;
P5=-5-4X+9X²-5X3
Soit f un endomorphisme dun K-espace
E. Etablir léquivalence suivante :
x IE le systÃme (x, f(x)) est lié f
est une homothétie vectorielle.
f désigne un endomorphisme dun K-espace vectoriel E.
a) On suppose quil existe un entier k non nul tel que f k=0
et f k-1 ¹0.
Montrer quil existe un vecteur a de
E tel que le systÃme (a, f(a),f
2(a),
,f k-1(a))
soit libre.
b) On suppose E de dimension finie n.
Montrer que si lendomorphisme f est
nilpotent, cest à dire si une puissance de f sannule, alors nécessairement f n=0.
Soient E et F deux K-espaces vectoriels et f un élément de LK(E,F).
a) Montrer que f est de rang 1 si et
seulement si il existe un vecteur b
non nul de F et une application K linéaire non nulle u de E vers K tels que pour tout x de E on ait f(x)=u(x).b
b) Si E=F en déduire une condition nécessaire et suffisante pour quun
endomorphisme de rang 1 soit un projecteur.
c) Plus généralement, soit r le rang
de lapplication K-linéaire f de E vers F. Montrer que f
peut se décomposer en une somme de r
applications linéaires de rang 1.
E, F, G désignent trois K espaces de dimension finie. f ILK(E, F) et gILK(F, G).
1) Montrer que Im(g![]() f)=g(Im(f)).
f)=g(Im(f)).
2) Montrer que rang(g![]() f)£ min( rang(f), rang(g) ) . (le plus petit des deux rangs).
f)£ min( rang(f), rang(g) ) . (le plus petit des deux rangs).
3) Etablir léquivalence : rang(g![]() f)=rang(f)
Im(f) Ker(g)=
f)=rang(f)
Im(f) Ker(g)=
4) Etablir léquivalence : rang(g![]() f)=rang(g) F=Im(f)+Ker(g).
f)=rang(g) F=Im(f)+Ker(g).
E, F, G trois K-espaces vectoriels de dimension finie. f ILK(E, F) et gILK(F, G).
1) Montrer que Ker(f)ÌKer(g![]() f)
f)
2) Montrer que Ker(g![]() f)=f 1(Ker(g))
f)=f 1(Ker(g))
3) Montrer que dimK(Ker(g![]() f) £ dimK(Ker(f))+dimK(Ker(g)
f) £ dimK(Ker(f))+dimK(Ker(g)
4) Etablir léquivalence dimK(Ker(g![]() f)=dimK(Ker(f))+dimK(Ker(g)) Ker(g) Ì
Im(f)
f)=dimK(Ker(f))+dimK(Ker(g)) Ker(g) Ì
Im(f)
5) Montrer que rang( g![]() f) ³ rang(f)+rang(g)-dimK(F).
f) ³ rang(f)+rang(g)-dimK(F).
E un K-espace vectoriel de dimension n et f un endomorphisme
de E.
On suppose quil existe un entier k
tel que Ker(f k)=Ker(f k+1)
Montrer que Ker(f k+1)=Ker(f k+2) et que E=Ker(f k)ÅIm(f k)
SOLUTIONS.
Les
trois vecteurs en question étant combinaisons linéaires dun mÃme
systÃme de deux vecteurs, le théorÃme fondamental assure leur
dépendance linéaire.
Pour une solution effective remplaçons suivant le schéma principal de la
démonstration, ![]() par
par ![]() =
=![]() dans les deux premiÃres égalités. On obtient
aprÃs simplifications :
dans les deux premiÃres égalités. On obtient
aprÃs simplifications :
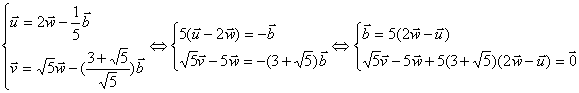
On obtient donc la relation de dépendance : ![]()
a)
DaprÃs les formules trigonométriques daddition on remarque que pour
tout x réel :
f1(x)=cos1sinx+sin1cosx ; f2(x)=cos1sinx-sin1cosx ; f3(x)=cos2sinx+sin2cosx
Si on note u la fonction classique
sinus de R dans R et v la fonction
cosinus, ce qui précÃde peut se résumer par les égalités
vectorielles :
f1=(cos1)u+(sin1)v ; f2=(cos1)u-(sin1)v ; f3=(cos2)u+(sin2)v.
On est donc en présence dun systÃme de 3 vecteurs tous combinaisons
linéaires du mÃme systÃme (u,
v) de deux vecteurs, donc formant
nécessairement un systÃme lié daprÃs le théorÃme
fondamental de la dimension.
b) Pour une relation effective on peut tirer des deux premiÃres égalités
une expression de (u, v) en fonction
de (f1, f2) que lon reporte dans la
derniÃre équation.
![]() ;
; ![]()
Soit, aprÃs simplifications : ![]()
VecR(S) est donc engendré par le systÃme réduit (f1, f2). Il est facile de vérifier que celui-ci est libre
car d une relation du type af bf =0 on déduit a=0 en écrivant légalité
fonctionnelle au point x=1 et b=0 en considérant limage de 1.
c) Les composantes de u=sin dans la
base (f1, f2) apparaissent dans les
calculs précédents..
Considérons
une relation de dépendance du type :
![]() E
E
Par regroupement des termes et puisque par hypothÃse le systÃme
initial S est libre, on en déduit que nécessairement : ![]()
Laissons de côté la premiÃre relation, particuliÃre vu le retour
de en à e1.
On voit alors facilement que, de proche en proche, ![]() pour tout k élément de . Ainsi
pour tout k élément de . Ainsi ![]() . En reportant cette expression dans la premiÃre
égalité non encore exploitée on obtient
. En reportant cette expression dans la premiÃre
égalité non encore exploitée on obtient ![]()
La discussion est claire :
_ Si n est impair, nécessairement a doit Ãtre nul et par suite tous
les autres coefficients considérés. Le systÃme S sera libre.
_ Si n est pair a peut Ãtre quelconque et il
existera donc des relations de dépendance non triviales entre les vecteurs de
S. Par exemple pour a =1 :
(e1+e2)-(e2+e3)+
+(-1)k+1(ek+ek+1)+
.+
(en-1+en)-(en+e1)=0E. S est lié.
Résolvons
par substitution élémentaire le systÃme traduisant lappartenance dun
quadruplet à E : ![]()
E apparait donc comme lensemble des vecteurs de R du type v=(x, y, -5x-2y, -2x-y)
avec pour (x, y) un couple quelconque de réels. En décomposant pour séparer le
rôle des deux paramÃtres on obtient E=
Ainsi E est le sous espace de R engendré par le systÃme(u,
v) de deux quadruplets
u=(1, 0, -5, -2) ; v=(0, 1, -2, -1). Reste à
remarquer que ce systÃme est libre.
En effet u ne peut Ãtre
multiple de v car sa premiÃre
composante est 1 alors que celle de v
est nulle, de mÃme lexamen des deuxiÃmes composantes montre que v ne peut Ãtre multiple de u.
E est un plan vectoriel de base (u, v).
Soit
x un vecteur de E. Par
hypothÃse ses termes de rang pair sont en progression arithmétique donc
régis par une formule élémentaire du type x2n=x0+nr.
De mÃme si r désigne la raison
de la progression arithmétique des termes dindice impair on peut écrire x2n+1=x1+nr pour tout entier n.
Considérons alors les quatre suites a,b,c,d
définies par les formules suivantes :
n IN
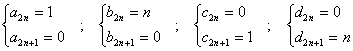
Il est clair que x se décompose sous
la forme x=x0a+rb+x1c+rd.
Le systÃme B =(a, b, c, d) engendre donc le R espace E.
De plus il sagit dun systÃme libre car de x=aa+ bb+ac+bd=0S on déduit dabord a=0 en écrivant x(0)=0, puis a=0 à partir de x(1)=0 et enfin b b=0 comme conséquence de x(2)=x(3)=0.
On a donc bien mis en évidence une base finie B de E et on peut conclure : dimR(E)=4.
En
séparant les rôles de chacun des paramÃtres on obtient la décomposition
naturelle :
(x+y-3z, x+2y-t, t+x-z)=x(1, 1, 1)+y(1, 2, 0)+z(-3, 0, -1)+t(0, -1, 1).
E est donc le sous-espace de R engendré par le systÃme S formé
des quatre triplets
u=(1, 1, 1) ; v=(1, 2, 0) ; w=(-3, 0, -1) ; j=(0,
-1, 1).
Déterminons le rang de S. grace à
la méthode du pivot de Gauss.
La matrice de S dans la base canonique de R est A=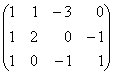
_ Les manipulations 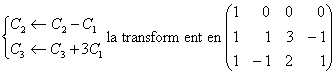
_ On poursuit avec 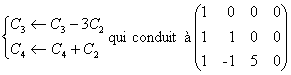
Le rang de S est donc égal à 3. En effet :
Lannulation de la derniÃre colonne est lexpression de légalité j=u-v
et le systÃme réduit aux 3 premiÃres colonnes est triangulaire
inférieur avec tous les coefficients diagonaux distincts de 0.
E est donc un sous-espace de R de mÃme dimension que celui-ci,
donc confondu avec lui. E=R . (u,
v, w) est bien sÃr une des
bases possibles.
_
Pour n=1, la propriété étudiée est
évidente car la fonction sinus nest pas la fonction identiquement nulle sur R et constitue donc bien à elle
seule un systÃme libre.
_ Supposons la propriété vraie au rang n ³1 et essayons den déduire que le
systÃme formé par les n+1
fonctions fk définies sur R par fk(x)=sin(kx) avec kI est encore libre.
Pour cela examinons les conséquences dune relation de dépendance du
type :
![]() .
.
DaprÃs les rÃgles élémentaires de dérivation il est clair que
pour tout entier k on a la relation
différentielle : fk=-k²fk . On en déduit, vu légalité précédente et la linéarité
de la dérivation : -a f a f -
.-n²anfn-(n+1)²an fn+1=0.
On peut alors combiner les deux relations précédentes de façon à
éliminer le terme en fn+1.
On obtient ![]()
DaprÃs lhypothÃse de récurrence à lordre n, tous les coefficients affectant les
vecteurs fk dans la
relation précédente sont nécessairement nuls.
Or k I (n+1)²-k²¹0. Tous les coefficients ak correspondants sont donc nuls et
.légalité initiale se résume à an fn =0 dont on tire immédiatement an =0 puisque fn+1 nest pas le zéro de lespace vectoriel.
La propriété de liberté étudiée est donc bien héréditaire , validée à
lordre 1, donc transmissible de proche en proche à tout entier
supérieur ou égal à 1.
Supposons maintenant f= ![]() . On en déduit que pour tout réel x, en multipliant par (cosx+2) :
. On en déduit que pour tout réel x, en multipliant par (cosx+2) : ![]() .
.
En utilisant ![]() la relation ci dessus
peut se condenser en légalité fonctionnelle :
la relation ci dessus
peut se condenser en légalité fonctionnelle : ![]()
( avec la convention f0=0).
Létude précédente nous permet dégaler les coefficients relatifs à un
mÃme vecteur fk et
donne le systÃme:
![]()
On en déduit facilement par un processus descendant lannulation de tous les
coefficients ak ce qui est incompatible avec la
premiÃre égalité. f ne peut
donc sécrire comme combinaison linéaire du systÃme (f1,
., fn).
La
somme étant supposée directe, on peut écrire 4=dimR(VecR(a,
b))+dimR(VecR(c, d)).
De plus, chacun des deux espaces constituant la somme est engendré par un
systÃme de deux vecteurs donc est de dimension au plus égale à 2.
La seule configuration compatible avec les remarques précédentes est donc dimR(VecR(a,
b))=dimR(VecR(c, d))=2.
Les deux couples générateurs (a, b)
et (c, d) constituent donc des bases des espaces respectifs engendrés et
lon sait que dans le cas de sous-espaces supplémentaires, la juxtaposition de
ces deux systÃmes constitue une base de lespace somme E.
S=(a, b, c, d) est donc une base de E.
Le remplacement de a par a+c ne modifie pas le rang et nous
conduit à la base (a+c,b,c,d)
De mÃme le remplacement de c
par 2c-(a+c) nous donne la base (a+c
,b, c-a, d)
Enfin léchange de c-a et d nous dit que S=(a+c, b, d, c-a) est une base de E.
On en déduit immédiatement la décomposition demandée : E=VecR(a+c)ÅVecR(b,d,c-a)
Si E nest plus supposé de dimension 4, laffirmation S base de E nest plus
assurée et la deuxiÃme décomposition peut savérer fausse. Par exemple
elle lest manifestement si a=0E
et si c¹0E car dans ce cas a+c=c-a=c vecteur non nul
appartenant aux deux sous-espaces que lon voudrait supplémentaires.
Envisageons
une relation de dépendance du type a f anfn=0.
On en déduit immédiatement par dérivation que sur R entier on a légalité :
![]() .
.
Puis, en posant X=x², que sur ]0,+¥[ : ![]()
Définissons alors pour tout k de
le polynôme  .
.
Légalité ci dessus équivaut avec ces notations à ![]() , toujours pour tout X >0.
, toujours pour tout X >0.
Or un polynôme à coefficients réels et admettant une infinité de racines
ne peut Ãtre que le polynôme identiquement nul. Légalité précédente est
donc vraie sur R entier et en particulier en tout
X=-k. On en déduit immédiatement ak=0 car Pj(-k)=0 j ¹k
La matrice représentant S dans la
base canonique de R est A=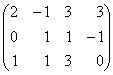
Les manipulations 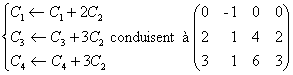 matrice dun
systÃme S de mÃme rang que S. Or il est clair que S est de rang
2 car les deux premiÃres colonnes de sa matrice représentative ne sont
pas proportionnelles alors que les deux derniÃres sont des multiples
évidents de la premiÃre. VecR(S)=VecR(e1, e2).
matrice dun
systÃme S de mÃme rang que S. Or il est clair que S est de rang
2 car les deux premiÃres colonnes de sa matrice représentative ne sont
pas proportionnelles alors que les deux derniÃres sont des multiples
évidents de la premiÃre. VecR(S)=VecR(e1, e2).
Pour compléter (e1, e2) en une base de R il suffit de lui adjoindre un vecteur v non combinaison linéaire de S cest
à dire pour lequel une égalité du type v=ae be est impossible. v=(0, 0, 1) est une des nombreuses possibilités !
On sait que lordre des vecteurs
dun systÃme ninflue pas sur le rang de celui ci.
On peut donc supposer sans restriction du problÃme que polynômes Pk seront rangés selon les
degrés strictement croissants.
Considérons alors une relation de dépendance non triviale du type a P1+
.+anPn=0 et notons r le
plus grand indice k tel que ak¹0.
_ Si r > 1on en déduit une expression de
Pr en fonction des
polynômes précédents : ![]() . Egalité impossible
car Pr serait alors
combinaison linéaire de polynômes de degré strictement inférieur à son
propre degré.
. Egalité impossible
car Pr serait alors
combinaison linéaire de polynômes de degré strictement inférieur à son
propre degré.
_ Si r=1, il reste a P1=0, impossible également
puisque a et P1
sont non nuls.
Le systÃme étudié ne peut donc Ãtre lié.
1) La vérification de la
structure de R-espace ne pose aucun
problÃme.
Pour la dimension, il suffit de remarquer quune matrice quelconque M de coefficient générique x(i, j) se décompose de maniÃre unique ![]() avec P= et U(i,j) matrice carrée dordre 3 dont tous les
éléments sont nuls excepté celui de la ligne i et la colonne j que
lon prend égal à 1.
avec P= et U(i,j) matrice carrée dordre 3 dont tous les
éléments sont nuls excepté celui de la ligne i et la colonne j que
lon prend égal à 1.
La dimension de lespace considéré est donc 9.
2) Pour létude de E, le plus simple consiste à essayer de construire
ces carrés magiques, sous la forme la plus générale. Pour cela notons que les
données de la valeur s des sommes
communes imposées, de lélément central c
et des deux éléments de la premiÃre ligne soient a et b déterminent de
proche en proche les valeurs restantes. En effet, deux éléments alignés sur une
ligne, colonne ou diagonale de la matrice étant connus, on trouve le
troisiÃme élément en amenant la somme à la valeur s. On aura par exemple aprÃs 6
opérations de ce type la structure 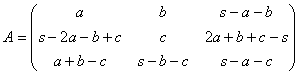
Dans ce schéma on na pas utilisé les contraintes des sommes sur les deux
derniÃres lignes de la matrice. Pour quelles soient réellement
réalisées on voit que la condition s=3c est nécessaire et suffisante, ce qui
nous donne une forme générale fonction des trois seuls paramÃtres a,b,c : 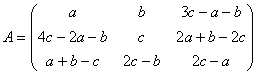 que lon peut
décomposer en :
que lon peut
décomposer en :
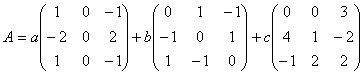 .
.
On a donc mis en évidence un systÃme générateur de E formé des trois
matrices apparaissant dans lécriture ci dessus et en situation dindépendance
car la combinaison précédente de maniÃre évidente ne peut donner la
matrice nulle que si les trois coefficients a, b,
c sont égaux à 0. E est donc un R-espace de dimension 3.
Notons P=VecR(u, v). Nous allons
montrer que tout supplémentaire G de F dans E est de dimension au plus 2.
Pour cela, soient x, y,
z trois vecteurs de G. DaprÃs lhypothÃse E =FÅP on peut les écrire sous la
forme ![]() avec f1, f2, f3
éléments de F.
avec f1, f2, f3
éléments de F.
Les vecteurs x-f1, y-f2, z-f3 sont alors élément du plan P donc nécessairement en
situation de dépendance linéaire. On peut donc trouver un triplet de réels non
identiquement nul, soit (a,b,c), tel
que : a(x-f1)+b(y-f2)+c(z-f3)=0E
En développant on peut écrire ax+by+cz=af1+bf2+cf3 égalité dont
le premier membre est situé dans le sous-espace G et le second membre
appartient à F.
Or par hypothÃse F G=, il sensuit que ax+by+cz=0E et que (x,y,z) est un systÃme lié. On a
bien dimR(G) £2.
G ne peut Ãtre réduit à car F ¹ E . Montrons que G ne peut
Ãtre une droite vectorielle. Il suffit de reprendre le raisonnement
précédent en inversant les rôles de P et G.
Si G=VecR(a) on peut
écrire u=f1+aa ; v=f2+ba avec f1, f2
éléments de F. Par suite le systÃme u-f1,
v-f2
sera lié. On en déduit comme précédemment lexistence dun couple de réels (x,y)
non identiquement nul tel que x(u-f1)+y(v-f2) =0E, puis à partir de xu+yv=xf1+yf2 légalité xu+yv=0E
car P F=.G ne peut donc
Ãtre que de dimension 2.
Sur la matrice représentant le
systÃme étudié dans la base canonique de R [X] les manipulations 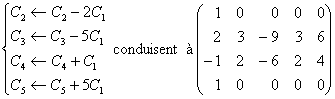
Les 4 derniÃres colonnes sont de maniÃre évidente
proportionnelles et les deux premiÃres non colinéaires. Le rang du systÃme est donc égal à 2.
_ Si f est une homothétie de rapport a, il est bien évident que pour
tout vecteur x de E le systÃme
(x, f(x))=(x,ax) est lié.
_ Réciproquement supposons que pour tout x
de E (x, f(x)) soit lié.
Soit a un vecteur non nul de E. Il
existe donc un scalaire a tel que f(a)=aa.
Pour tout x multiple de a on a encore f(x)=ax. En effet on peut écrire x=ba , doà par linéarité de f : f(x)= f(ba b
f(a)=b aa a ba ax
Montrons que
lon a encore f(x)=ax si (a, x) est un
systÃme libre.
Par hypothÃse il existe deux scalaires b et l tels que f(x)=bx et f(a+x)=l(a+x).
Or, par linéarité de f on aura :
l(a+x)= f(a+x)=
f(a)+ f(x)=aa+bx.
Le systÃme (a, x) étant supposé libre, on en déduit a l b et donc f(x)=ax
f nest donc autre que lhomothétie
vectorielle de rapport a
a) Par hypothÃse f k-1est
non nulle, il existe donc au moins un vecteur, soit a, dont limage
f
k-1(a) ne soit
pas le vecteur nul de E .
Montrons alors que le systÃme S= (a,
f(a),
f 2(a),
, f k-1(a)) est libre. Supposons pour cela une
combinaison linéaire du type ![]()
En prenant limage par f k-1
on en déduit vu la linéarité et lhypothÃse de nilpotence f k=0 :
a f
k (a)=0E et par
suite a =0 puisque f k-1(a)
est non nul.
De mÃme en prenant limage par f
k-2 il ne restera que a f
k (a)=0E. dont on déduit a =0.
De proche en proche, en prenant les images par les puissances dordre q de f,
q variant en décroissant de k-3 à 0, on en déduit que tous
les coefficients ak-q sont nuls.
Le systÃme S est bien libre.
b) _ Si f k=0 pour un
entier k inférieur à la
dimension n de E on en déduit
immédiatement en composant avec f
n-k que : f n=0.
_ Si lannulation dune puissance de
f est réalisée pour un exposant
strictement supérieur à n,
notons k le plus petit entier
supérieur ou égal à n tel que f k=0.
Par minimalité de k, on a donc f k-1¹0 et daprÃs létude faite
précédemment, il existe un vecteur a
de E tel que S= (a, f(a),
f 2(a),
, f k-1(a)) soit libre. Ceci entraine que le
cardinal de S, soit k , est au plus
égal à n dimension de lespace E. Ainsi k=n
et f n=0.
a) _ Si pour tout x de E f(x)=u(x)b , lespace image Im(f ) est inclus dans la droite
vectorielle engendrée par b. Si de
plus u est supposé non nulle, il
existera au moins un x de E tel que u(x)¹0 et donc pour lequel f(x)¹0E.
Le sous-espace Im(f) nest donc pas
réduit au sous-espace nul, est inclus dans la droite VecK(b) donc coÃncide avec cette droite
vectorielle. f est de rang 1.
_ Réciproquement, si f est supposé de rang 1, lespace image
Im(f) est une droite engendrée par un
vecteur non nul b. Notons alors u lapplication de E vers K qui à tout x de E fait correspondre la composante sur b de son image f(x). :
xIE f(x)=u(x)b
Il nous reste à montrer que f
est linéaire. Soient x et y quelconques dans E et a scalaire.
Par définition de u on a : f(x)=u(x)b ;
f(y)=u(y)b ; f(ax+y)=u(ax+y)b.
Puis, par linéarité de f, on peut
écrire : u(ax+y)b=a(u(x)b)+u(y)b.
b étant non nul, on en déduit u(ax+y au(x)+u(y).
(Lapplication u nest pas
identiquement nulle puisque Im(f) nest
pas réduit à ).
b) Avec les notations précédentes on peut écrire :
xIE f![]() f(x)=
f(u(x)b)=u(x) f(b)=u(x)u(b)b. On aura donc f 2=f xIE u(x)=u(x)u(b)
f(x)=
f(u(x)b)=u(x) f(b)=u(x)u(b)b. On aura donc f 2=f xIE u(x)=u(x)u(b)
Ceci étant en fait équivalent à u(b)=1 car u nest pas lapplication nulle.
Or u(b)=1
f(b)=b
. Un endomorphisme f de rang 1 est
donc une projection si et seulement si il existe un vecteur non nul b invariant pour f.
f est alors la projection sur VecK(b) parallÃlement à Ker(f)
c) Soit maintenant f de rang r et considérons une base B = (b1,
,.br) de Im(f).
Pour tout x de E on peut donc écrire f(x)=![]() en désignant par uk(x) la composante dordre k de f(x)
dans la base B . On montre aussi facilement que
dans a) le caractÃre linéaire de chacune des applications uk . Remarquons pour conclure
quaucune de ces applications nest nulle, sinon Im(f) serait inclus dans un espace de dimension strictement inférieur
à r, ceci en contradiction
avec rang(f)=r.
en désignant par uk(x) la composante dordre k de f(x)
dans la base B . On montre aussi facilement que
dans a) le caractÃre linéaire de chacune des applications uk . Remarquons pour conclure
quaucune de ces applications nest nulle, sinon Im(f) serait inclus dans un espace de dimension strictement inférieur
à r, ceci en contradiction
avec rang(f)=r.
On a donc bien écrit f comme
somme de r applications de rang 1,
les applications fk définies sur E par fk(x)=uk(x)bk.
1) Im(g![]() f)===g(Im(f))
f)===g(Im(f))
2) _ On vient de voir que Im(g![]() f) est un sous-espace de Im(g), on a donc nécessairement dimK(Im(g
f) est un sous-espace de Im(g), on a donc nécessairement dimK(Im(g![]() f £ dimK(Im(g)), soit : rang(g
f £ dimK(Im(g)), soit : rang(g![]() f £rang(g).
f £rang(g).
_ On sait que tout morphisme de K-espace transforme un sous-espace de
dimension finie r du départ en un
sous-espace à larrivée de dimension au plus r. On aura donc en particulier rang(g![]() f)=dimK(g(Im(f)))
£ dimK(Im(f))=rang(f).
f)=dimK(g(Im(f)))
£ dimK(Im(f))=rang(f).
3) Plus précisément, on sait que dimK(g(Im(f)))=dimK(Im(f))-dimK(Im(f) Ker(g))
On a donc rang(g![]() f)=rang(f)
dimK(Im(f) Ker(g))=0
Im(f) Ker(g)=.
f)=rang(f)
dimK(Im(f) Ker(g))=0
Im(f) Ker(g)=.
4) On a vu que Im(g![]() f) est un sous-espace de Im(g). On a donc une premiÃre
équivalence simple : rang(g
f) est un sous-espace de Im(g). On a donc une premiÃre
équivalence simple : rang(g![]() f)=rang(g)
Im(g
f)=rang(g)
Im(g![]() f)=Im(g).
f)=Im(g).
Etudions maintenant cette égalité ensembliste.
_ Si Im(g![]() f)=Im(g).
f)=Im(g).
Pour tout vecteur y de F on pourra
dire que g(y) admet au moins un antécédent x
pour g![]() f, donc sécrira g(y)= g
f, donc sécrira g(y)= g![]() f(x). On en déduit lexistence dun vecteur n de Ker(g) pour lequel y= f(x)+n.
Ainsi F coÃncide avec la somme des deux sous-espaces Im(f) et Ker(g).
f(x). On en déduit lexistence dun vecteur n de Ker(g) pour lequel y= f(x)+n.
Ainsi F coÃncide avec la somme des deux sous-espaces Im(f) et Ker(g).
_ Si F=Im(f)+Ker(g).
Tout élément de Im(g) est par
définition du type z=g(y)
avec y vecteur de F donc pouvant se
décomposer par hypothÃse en somme y=f(x)+n avec xIE et
nIKer(g).
Par linéarité de g on en déduit :
z=g(y)=g( f(x))+g(n)= g![]() f(x)+0G= g
f(x)+0G= g![]() f(x).
f(x).
Ainsi z appartient à Im(g![]() f).
f).
On a donc bien légalité Im(g![]() f)=Im(g) de par la double inclusion.
f)=Im(g) de par la double inclusion.
Remarquons la synthÃse intéressante des deux derniÃres
questions :
F=Im(f)ÅKer(g)
rang(g![]() f)=rang(f)=rang(g).
f)=rang(f)=rang(g).
1) Si x appartient à Ker(f)
on a, par définition , f(x)=0F, puis par linéarité de g, g( f(x))=0G
exprimant lappartenance de x
à Ker(g![]() f). On a bien Ker(f)ÌKer(g
f). On a bien Ker(f)ÌKer(g![]() f).
f).
2) xIKer(g![]() f) g( f(x))=0G f(x)IKer(g)
xIf (Ker(g)).
f) g( f(x))=0G f(x)IKer(g)
xIf (Ker(g)).
3) On sait daprÃs le théorÃme du rang que :
dimK f(f -1(Ker(g)))=dimKf -1(Ker(g))-dimK(Ker(f) f (Ker(g)))
Or on a vu Ker(f)ÌKer(g![]() f)=f -1(Ker(g)). Légalité ci dessus se simplifie donc en :
f)=f -1(Ker(g)). Légalité ci dessus se simplifie donc en :
dimK f(f -1(Ker(g)))=dimKKer(g![]() f)-dimK(Ker(f)).
f)-dimK(Ker(f)).
Il suffit maintenant de rappeler linclusion évidente f(f -1(Ker(g))Ì Ker(g) pour conclure linégalité demandée : dimKKer(g![]() f)£dimKKer(f)+dimKKer(g)
f)£dimKKer(f)+dimKKer(g)
4) DaprÃs les calculs précédents, linégalité obtenue est une égalité
si et seulement si
f(f
-1(Ker(g))
coÃncide avec Ker(g).
Montrer cette égalité équivaut à établir linclusion : Ker(g)Ì f(f-1(Ker(g)))
_ Il est clair que cette relation entraine également Ker(g)Ì
Im(f).
_ Réciproquement, si Ker(g)Ì Im(f), tout y de Ker(g) pourra sécrire image y=f(x)
dun vecteur x de E. Mais cet x appartiendra à f-1(Ker(g)) puisque son image y
est dans Ker(g).
Ainsi y est par définition élément de
f(f-1(Ker(g))).
On a donc bien : dimK(Ker(g![]() f)=dimK(Ker(f))+dimK(Ker(g)) Ker(g) Ì
Im(f)
f)=dimK(Ker(f))+dimK(Ker(g)) Ker(g) Ì
Im(f)
5) DaprÃs le théorÃme du rang on peut écrire les égalités :
dimK(E)=rang(f)+dimK(Ker(f)) (Pour f ILK(E,F)).
dimK(F)=rang(g) +dimK(Ker(g)) (Pour g I LK(F,G) ).
dimK(E)=rang(g![]() f)+dimK(Ker(g
f)+dimK(Ker(g![]() f)) (Pour g
f)) (Pour g![]() f I LK(E,G)) .
f I LK(E,G)) .
On en déduit rang(g![]() f)=dimK(E)-dimK(Ker(g
f)=dimK(E)-dimK(Ker(g![]() f))³ dimK(E)-dimK(Ker(f))-dimK(Ker(g))
f))³ dimK(E)-dimK(Ker(f))-dimK(Ker(g))
daprÃs la troisiÃme relation et linégalité de la question 3.
Les deux premiÃres formules conduisent ensuite à la minoration demandée :
rang( g![]() f ³ rang(f)+rang(g)-dimK(F).
f ³ rang(f)+rang(g)-dimK(F).
_ Linclusion Ker(f k+1)Ì Ker(f k+2) est évidente car f k+1(x)=0E
Þ f(f k+1(x))=f(0E)=0E.
_Réciproquement, si f k+2(x)=0E, on peut écrire f k+1(f(x))=0E,
ou encore f(x)IKer(f k+1)
Or daprÃs lhypothÃse, ce noyau coÃncide avec Ker(f k).
On en déduit donc f k(f(x))=0E
, cest à dire x élément de
Ker(f k+1).
De proche en proche, en répétant le raisonnement précédent, on peut établir que
les noyaux des puissances dordre q
de f sont confondus avec Ker(f k) pour tout entier q ³k
En utilisant le
théorÃme du rang on en déduit alors que les espaces images de ces
puissances sont tous égaux à Im(f
k).
En effet pour q ³k on a de maniÃre évidente :
Im(f
q)ÌIm(f k) , ainsi que la relation :
rang(f q)=dimK(E)-dimK(Ker(f q))=dimK(E)-dimK(Ker(f k))=rang(.f k)
En particulier on peut dire Im(f 2k)=Im(f k). Pour tout vecteur x de E on aura donc :
f 2k(x)= f k(x) , cest à dire x= f
k(x)+n avec nIKer(f k).
On a donc déjà la décomposition en somme : E=Im(f k)+Ker(f k).
Vérifions quelle est directe. Soit y
commun aux deux sous-espaces composants.
On peut donc lécrire sous la forme y=
f k(x) avec xIE et f k(y)=0E.
Mais alors, par composition : f 2k(x)=0E,
cest à dire xIKer(f 2k)=Ker(f k).
On en déduit y= f k(x)=0E.
La somme est bien directe.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1192
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved