| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
On a été constate par expérience que tout corps dans la nature est une source de rayonnement électromagnétique, dont les caractéristiques dépendent tant de la nature des corps que de leur température. Par cette raison, ce type de rayonnement a été nommé rayonnement thermique. La cause du rayonnement thermique est le mouvement d'agitation thermique des atomes ou des molécules, qui a comme résultat leur excitation énergétique par des collisions et, plus tard, leur désexcitation par l'émission de rayonnement électromagnétique. L'ensemble de ces rayonnements de désexcitation est le rayonnement thermique lui-mÊme.
Si on introduit un corps chauffé dans une enceinte fermée, à parois réfléchissants et isolée adiabatiquement de l'extérieur, on pourra atteindre dans le temps l'équilibre entre le rayonnement thermique émis par le corps et le rayonnement absorbé par les corps de l'enceinte. Dans ce cas, on dit qu'à l'intérieur de l'enceinte il y a un rayonnement thermique d'équilibre. On peut considérer le rayonnement thermique d'équilibre comme un systÈme thermodynamique à l'équilibre qui a les propriétés suivantes:
Þ il est homogÈne et isotrope
Þ il a un spectre continu
Þ il est non-polarisé
Le rayonnement thermique d'équilibre possÈde une certaine énergie interne U. Puisqu'il est homogÈne et isotrope il peut Être caractérisé par la densité d'énergie w, qui représente l'énergie totale du rayonnement thermique contenu dans le volume unitaire de l'enceinte
![]()
Quoique le spectre du rayonnement thermique d'équilibre soit continu, l'énergie n'est pas également distribuée entre toutes les longueurs d'onde qu'il les contient. La modalité de distribution de l'énergie du rayonnement thermique en fonction de la longueur d'onde est décrite par la grandeur physique nommée densité spectrale d'énergie, symbolisée par wl et définie comme la quantité d'énergie rayonnante qui correspond à l'unité de longueur d'onde et au volume unitaire
![]()
Si on considÈre un corps quelconque en contact avec un rayonnement externe, il y a trois phénomÈnes possibles:
Þ réflexion d'une partie de ce rayonnement, mesurée par le coefficient de réflexion r, défini comme le rapport entre les flux de rayonnement réfléchi et incident

Þ transmission d'une partie de ce rayonnement à travers le matériau du corps, mesurée par le coefficient de transmission t, défini comme le rapport entre les flux de rayonnement transmis et incident

Þ absorption d'une autre partie du rayonnement et sa transformation dans d'autres formes d'énergie, mesurée par le coefficient absorption a, défini comme le rapport entre les flux de rayonnement absorbé et incident
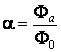
|
|
Selon la loi de la conservation de l'énergie, on obtient
![]()
D'habitude, tant le coefficient d'absorption que les coefficients de transmission ou de réflexion dépendent de la longueur d'onde du rayonnement incident, aussi bien que de la nature ou de la température du corps. Un corps dont le coefficient d'absorption est unitaire
a
pour toutes les longueurs d'onde du rayonnement incident et pour toute température s'appelle corps noir absolu . Dans la nature, on ne peut pas trouver des corps noirs absolus, ceux-ci étant des objets idéals, mais on pourrait construire des dispositifs qui peuvent les modeler en bonnes conditions.
Le corps noir expérimental consiste d'une enceinte sphérique, munie d'un petit orifice. Le rayonnement qui pénÈtre par l'orifice subit des multiples réflexions sur la paroi intérieur de la cavité, aboutissant par Être complÈtement absorbé. On peut chauffer la paroi de l'enceinte ainsi qu'elle deviendra une source de rayonnement thermique. Une partie de ce rayonnement peut quitter l'enceinte à travers l'orifice, ce qui transforme l'enceinte en source de rayonnement thermique.
|
|
Le rayonnement thermique émis par un corps chauffé est décrit par la grandeur physique nommée densité intégrale de rayonnement, notée par M et définie comme la quantité d'énergie émise pendant l'unité de temps par la surface unitaire du corps
![]()
|
|
On peut aussi écrire
![]()
car l'énergie émise pendant l'unité de temps représente le flux d'énergie rayonnante.
Pour un corps donné, l'énergie émise n'est pas également distribuée par rapport à la longueur d'onde. La modalité par laquelle la distribution de l'énergie est partagée en fonction de la longueur d'onde est mesurée par la grandeur physique nommée densité spectrale de rayonnement
![]()
La densité spectrale de rayonnement est la quantité d'énergie émise pendant l'unité de temps et dans l'unité de longueur d'onde par la surface unitaire d'un corps rayonnant.
En considérant un systÈme physique formé d'un corps noir et le rayonnement thermique, à l'équilibre thermodynamique, il résulte
dWabsorbé = dWincident (corps noir, a
dWabsorbé = dWémis (équilibre thermodynamique)
Donc
dWincident = dWémis
c'est-à-dire le rayonnement issu d'un corps noir a les mÊmes caractéristiques que le rayonnement thermique avec lequel il est en équilibre. De la il résulte la possibilité pratique d'étudier le rayonnement thermique d'équilibre, en mesurant les caractéristiques du rayonnement du corps noir en équilibre avec celui-ci.
Puisque le flux du rayonnement thermique incident est proportionnel à la densité d'énergie du rayonnement thermique, il résulte qu'entre la densité intégrale de rayonnement du corps noir et la densité d'énergie du rayonnement thermique avec lequel le corps noir est à l'équilibre il y a une relation de proportionnalité
![]()
De mÊme il existe une relation de proportionnalité entre la densité spectrale de rayonnement et la densité spectrale d'énergie
![]()
Par expérience, on constate que la densité spectrale de rayonnement d'un corps noir dépend seulement de sa température absolue et de la longueur d'onde, sans dépendre de la nature, de la forme géométrique et des dimensions du corps
ml = ml l,T)
Par l'intégration de la densité spectrale de rayonnement en fonction de la longueur d'onde, on obtient
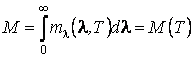
c'est-à-dire la densité intégrale de rayonnement du corps noir est une fonction universelle de sa température absolue.
Parce que la densité spectrale de rayonnement est proportionnelle à la densité spectrale d'énergie du rayonnement thermique d'équilibre, il résulte que celle-ci est aussi une fonction universelle de température et de la longueur d'onde
wl = wl l,T)
et la densité d'énergie de ce rayonnement ne dépend que de la température absolue
w = w(T)
|
|
Pour offrir une explication théorique de cette loi, on va considérer un systÈme formé par deux corps noirs, mécaniquement isolés entre eux et ayant la mÊme température absolue T. Les corps peuvent faire des échanges d'énergie seulement par l'intermédiaire du rayonnement thermique, filtré ainsi qu'il contiendrait une seule composante monochromatique. On observe que:
Þ l'énergie émise par l'un de deux corps est absorbée par l'autre et vice-versa
Þ si la densité spectrale d'énergie rayonnante émise par l'un des corps serait plus grande que celle émise par l'autre corps, alors il en résulterait l'existence d'un transfert d'énergie, sous forme de chaleur, d'un corps à l'autre
Þ mais, puisque les corps ont la mÊme température, ils sont en équilibre thermodynamique et, selon le deuxiÈme principe de la thermodynamique, l'échange de chaleur se produit seulement accompagné par un échange de travail
Þ comme les corps sont mécaniquement isolés, il résulte que l'échange de chaleur est nul
Þ la conclusion est que l'hypothÈse selon laquelle la densité spectrale d'énergie rayonnante d'un corps diffÈre de celle du autre corps est fausse, en démontrant ainsi théoriquement la loi de Kirchhoff.
Par expérience, on constate que la densité intégrale de rayonnement d'un corps noir est proportionnelle à la quatriÈme puissance de sa température absolue
M(T) = sT
Dans cette expression s s'appelle la constante de Stefan-Boltzmann et a la valeur
s = 5,67 10-8 W/(m2K4)
En essayant une démonstration théorique de cette loi on va considérer un systÈme thermodynamique composé par le rayonnement thermique d'équilibre, à l'intérieur d'une enceinte fermée. Le rayonnement de l'enceinte exerce une pression sur la paroi. Conformément à la relation d'Einstein entre la masse et l'énergie
W = mc2
il résulte qu'un flux d'énergie est équivalent à un transport de masse qui s'effectue avec la vitesse de propagation du flux d'énergie. Cela signifie que le rayonnement ayant le flux F transporte dans chaque seconde vers la paroi de l'enceinte l'impulsion

Le flux d'énergie incident dépend de la composante perpendiculaire sur la paroi de la densité du courant d'énergie et de l'aire de la paroi
![]()
Conformément aux lois du rayonnement électromagnétique, la densité du courant d'énergie est proportionnelle à la densité d'énergie des ondes électromagnétiques
![]()
Le rayonnement thermique d'équilibre est homogÈne et isotrope, ce qui signifie que la densité du courant d'énergie dans tout point est nulle, donc les rayonnements qui y sont présents se propagent dans toutes les directions possibles. Une telle situation est équivalente à l'affirmation que dans la direction de chaque axe de coordonnée il y a deux courants d'énergie, égaux en module, mais de sens opposés. Il y a, par conséquent, six composantes de la densité de courant d'énergie (trois axes deux sens pour chaque axe) qui transportent des quantités égales d'énergie. La composante qui nous intéresse, I , est l'une des six composantes et transporte l'énergie
![]()
L'expression de l'impulsion transporté vers la paroi dans l'unité de temps devient
![]()
Quand la paroi est parfaitement réfléchissante, la variation de l'impulsion du rayonnement consécutive à l'interaction avec la paroi est donnée par la différence entre l'impulsion du rayonnement réfléchi et l'impulsion du rayonnement incident. Dans l'unité de temps, cette variation d'impulsion a l'expression

Cette variation d'impulsion du rayonnement peut Être interprétée comme l'effet de l'action d'une force de la part de la paroi contre le rayonnement incident. La réaction de cette force justifie, à son tour, la pression exercée sur la paroi
![]()
c'est-à-dire la pression exercée sur la paroi de l'enceinte par le rayonnement thermique d'équilibre est numériquement égale à un tiers de la densité d'énergie du rayonnement.
Quand on utilise le modÈle photonique du rayonnement, le résultat final est le mÊme. Dans ce cas, le rayonnement thermique d'équilibre est associé à un gaz, formé par des photons, et la pression est due aux collisions entre les photons et la paroi de l'enceinte. On connait l'équation thermique d'état d'un gaz parfait
![]()
D'autre part, l'équation calorique d'état a la forme suivante
![]()
oÙ i est le nombre de degrés de liberté de la molécule. Un photon a six degrés de liberté (trois directions de translation, chacune à deux possibilités de polarisation). L'énergie interne du gaz photonique peut Être exprimée en fonction de la densité d'énergie
![]()
En divisant la premiÈre équation par la deuxiÈme équation, il résulte

Selon le premier principe de la thermodynamique on peut écrire
![]()
ou
![]()
oÙ S est l'entropie du systÈme thermodynamique. De cette relation, on va trouver l'expression de la variation élémentaire de l'entropie
![]()
Selon la loi de Kirchhoff,
![]()
En substituant dans l'équation, on obtient
![]()
L'entropie est une fonction d'état. La conséquence mathématique est que l'entropie est une fonction à différentielle totale exacte, ainsi qu'on peut écrire

Il résulte
![]()
ou
![]()
Par l'intégration on obtient
![]()
ou
![]()
Parce que la densité d'énergie du rayonnement thermique est proportionnelle à la densité intégrale de rayonnement du corps noir, il résulte
![]()
c'est-à-dire justement la loi de Stefan-Boltzmann.
|
|
Le résultat de l'étude de la densité intégrale de rayonnement du corps noir est compris dans une courbe de distribution de l'énergie rayonnante en fonction de la longueur d'onde.
La figure ci-jointe présente deux courbes, tracées pour deux températures différentes. On peut observer que les longueurs d'onde pour lesquelles les densités spectrales d'énergie sont maxima dépendent de la température absolue du corps noir. La loi de déplacement de Wien montre que le produit entre la température absolue du corps noir et la longueur d'onde correspondante au maximum de la courbe de distribution a une valeur constante
l T l T = const
On peut utiliser encore une fois les lois de la thermodynamique pour démontrer la loi de déplacement de Wien.
|
|
Soit une enceinte sphérique, contenant du rayonnement thermique d'équilibre. Le rayonnement de l'enceinte peut Être modelé comme un systÈme d'ondes stationnaires. Par une transformation adiabatique, peuvent varier tant la température que la distribution des ondes stationnaires. Ainsi l'onde stationnaire, de longueur d'onde l, qui 's'appuie' dans les points A et B de l'enceinte, sera replacée par une autre onde stationnaire, de longueur d'onde l', qui s'étend entre les mÊmes points. Il résulte
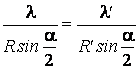
ou

D'autre part, puisque dans une transformation adiabatique dQ = 0, il résulte
![]()
En utilisant la loi de Stefan-Boltzmann, on obtient

ou
![]()
Par l'intégration, on obtient
![]()
ou
![]()
Alors

D'autre part
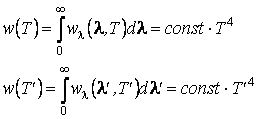
De la
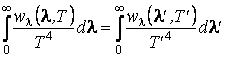
Mais
![]()
donc
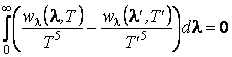
Il résulte
![]() = constante de la transformation
adiabatique considérée
= constante de la transformation
adiabatique considérée
En notant
![]()
et en observant que n'importe quelle fonction de u est aussi une constante de la transformation adiabatique, il résulte
![]()
ou
![]()
c'est-à-dire la densité spectrale d'énergie est proportionnelle à une fonction universelle, qui ne dépend que du produit entre la longueur d'onde du rayonnement et la température absolue du corps noir.
L'extremum de la courbe de distribution correspond à la condition
![]()
La valeur du u pour laquelle cette condition est remplie vérifie les égalités
![]()
ce qui représente justement la loi de déplacement de Wien.
On peut aussi démontrer la loi de déplacement de Wien en utilisant la théorie photonique. On sait que l'énergie cinétique la plus probable d'une molécule de gaz parfait est proportionnelle à la température absolue du gaz. En considérant que dans le gaz photonique cette propriété reste valable, il résulte

Selon la relation de Planck
![]()
ainsi que
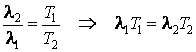
Le dernier problÈme à résoudre qui restait devant les théoriciens était de trouver la relation mathématique capable d'expliquer la forme de la courbe de distribution de l'énergie rayonnante en fonction de la longueur d'onde. Le modÈle théorique était l'ensemble d'ondes stationnaires décrit dans le chapitre précÈdent. On peut considérer que l'énergie avec laquelle contribuent les rayonnements de longueur d'onde l de l'enceinte est proportionnelle au nombre de ventres de ces rayonnements et à l'énergie moyenne associée à un tel ventre. Pour calculer le nombre de ventres on fait l'hypothÈse que le volume de l'enceinte est rempli par des tétraÈdres réguliers, chacun côté, de longueur l/2, étant un fuseau de l'onde stationnaire (le fuseau est borné par deux noeuds et a au centre un ventre). Vu que le volume d'un tétraÈdre est proportionnel à la troisiÈme puissance de la longueur du côté
![]()
il résulte que le nombre de ventres est proportionnel au volume de l'enceinte et à l'inverse de la troisiÈme puissance de la longueur d'onde
![]()
Si on note avec <e> l'énergie moyenne attribuée à un fuseau (ainsi nommé mode de vibration), on obtient l'expression de la densité spectrale d'énergie sous la forme
![]()
Pour le calcul de l'énergie moyenne qui revient à un mode de vibration on a été fait l'hypothÈse que l'énergie d'un fuseau peut prendre n'importe quelle valeur, mais que la probabilité d'une valeur donnée de l'énergie este de type maxwellien
![]()
expression dans laquelle k est la constante de Boltzmann et C est une constante est déterminée avec la relation
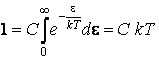
Dans ces conditions, l'énergie moyenne d'un mode de vibration est
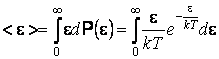
Vu que

ou
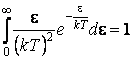
il résulte
![]()
Finalement
![]()
Cette forme de la fonction de distribution de la densité spectrale par rapport avec la longueur d'onde et la température porte le nom de 'loi de Rayleigh-Jeans'.
Malheureusement ce résultat théorique vient en contradiction avec les observations expérimentales, suivant la courbe expérimentale seulement dans le domaine des grandes longueurs d'onde. L'échec de l'explication théorique du mode de distribution spectrale de l'énergie rayonnante a été, à son temps, extrÊmement grave, parce que la démonstration était basée sur les lois fondamentales de la thermodynamique et de l'électromagnétisme et l'absence de leur validité dans ce domaine mettait à l'épreuve mÊme les fondements de la physique.
Un autre essai, appartenant à Wien, de trouver la formule de la densité spectrale de l'énergie a été concrétisé dans la relation

nommée la loi de Wien. Mais, encore une fois, l'expression théorique contredisait les résultats expérimentaux, à seule différence que cette fois-ci l'approximation était correcte dans le domaine des petites longueurs d'onde.
|
|
Ainsi, au début du vingtiÈme siÈcle, la physique était dans une vraie situation de crise, parce que les connaissances de thermodynamique et de théorie des ondes électromagnétiques, unanimement acceptées, ne pouvaient pas expliquer les lois expérimentales du rayonnement thermique du corps noir. La sortie de l'état de crise s'était produit par l'acceptation de la théorie photonique de la lumiÈre comme alternative à la théorie ondulatoire.
Planck était le physicien qui, introduisant le concept de photon, a montré que l'énergie moyenne attribuée à un mode de vibration doit Être calculée d'une toute autre maniÈre. Selon Planck, le rayonnement thermique est constitué par des photons, chacun d'eux ayant une énergie
![]()
Dans ces conditions, l'énergie d'un mode de vibration ne peut plus varier de façon continue, mais seulement par des quantités discrÈtes, égales avec au moins à l'énergie d'un photon. Par cette raison, les opérations d'intégration effectuées auparavant doivent Être substituées par des opérations de sommation. L'énergie totale d'un mode de vibration dépend seulement du nombre n de photons correspondants
![]()
La probabilité que l'énergie ait cette valeur décroit exponentiellement avec la croissance de la valeur de l'énergie
![]()
Evidemment, chacun mode de vibration a une certaine valeur de l'énergie, ce qui signifie que la probabilité en question est normée
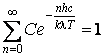
On calcule l'énergie moyenne par la sommation de toutes les valeurs possibles de l'énergie, pondérées par la probabilité d'apparition de ces valeurs

En notant ![]() , on observe
que
, on observe
que

De mÊme
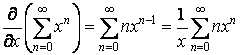
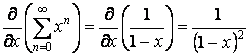
ainsi que

Donc
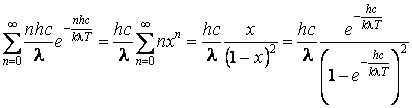
Il résulte

ou
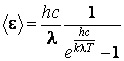
L'expression de la fonction de distribution de l'énergie devient

Cette expression est connue sous le nom de loi de Planck, ayant la qualité qu'elle suit parfaitement la courbe expérimentale. De plus, le fait que les lois de Rayleigh-Jeans et Wien sont de bonnes approximations pour certaines régions de la courbe expérimentale peut s'expliquer par cela qu'elles sont des approximations de la loi de Planck correspondantes aux grandes longueurs d'onde, respectivement aux petites longueurs d'onde. Ainsi
Þ
si 
Þ
si 
On peut reprocher à la démonstration de Planck le caractÈre inconséquent. Plus précisément, il utilise l'hypothÈse de la structure photonique du rayonnement thermique (à base duquel on calcule l'énergie moyenne d'un mode de vibration) en mÊme temps que l'hypothÈse ondulatoire (à base duquel on calcule le nombre de modes de vibration). Pour éliminer les lacunes de cette théorie, Einstein a proposé une nouvelle variante de démonstration de la loi de Planck, basée sur un modÈle purement quantique.
Selon le modÈle d'Einstein, le rayonnement thermique est le résultat des processus d'absorption ou d'émission d'énergie qui se produisent au niveau des atomes qui composent le corps noir. Les atomes absorbent ou émettent d'énergie seulement en quantités bien déterminées, correspondantes à la différence entre les états énergétiques permis. Ainsi, prenant en considération un état énergétique fondamental e et un état énergétique excité e , l'atome peut passer du premier état dans le deuxiÈme état seulement par l'absorption d'un photon d'énergie
|
e N2 e N1 |
|||||||||||||||||||||
e e e
et longueur d'onde
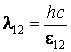
Le nombre d'atomes trouvés dans l'état fondamental est N1, et le nombre d'atomes de l'état excité est N2. On peut imaginer trois types de processus qui conduisent à la modification du nombre d'atomes de chacun état:
Þ absorption stimulée ou le processus par lequel sous l'influence des rayonnements de longueur d'onde l l'atome passe de l'état fondamental dans l'état excité par l'absorption d'un photon. Le nombre d'atomes qui participent aux tels processus est proportionnel à l'intervalle de temps pris en considération (dt), au nombre d'atomes en état fondamental (N1) et à la densité spectrale d'énergie du rayonnement incident correspondant à la longueur d'onde l
![]()
Le signe moins indique le fait que le nombre d'atomes en état fondamental diminue. Le coefficient B12 s'appelle le coefficient d'Einstein d'absorption stimulée.
Þ émission stimulée ou le processus par lequel sous l'influence des rayonnements de longueur d'onde l l'atome passe de l'état excité dans l'état fondamental par l'émission d'un photon. Le nombre d'atomes qui participent aux tels processus est proportionnel à l'intervalle de temps pris en considération (dt), au nombre d'atomes en état excité (N2) et à la densité spectrale d'énergie du rayonnement incident correspondant à la longueur d'onde l
![]()
Le coefficient B21 s'appelle le coefficient d'Einstein d'émission stimulée.
Þ émission spontanée ou le processus par lequel l'atome passe par soi-mÊme de l'état excité dans l'état fondamental par l'émission d'un photon. Le nombre d'atomes qui participent aux tels processus est proportionnel à l'intervalle de temps pris en considération (dt) et au nombre d'atomes en état excité (N2)
![]()
oÙ le coeffficient A21 s'appelle le coefficient d'Einstein d'émission spontanée.
À l'équilibre les nombres d'atomes de l'état fondamental ou de l'état excité sont constants, en résultant
![]()
ou
![]()
ou 
En considérant que le nombre d'atomes trouvés dans un certain état énergétique obéit à une statistique maxwellienne, il résulte
![]()
En substituant dans l'expression de la densité spectrale d'énergie, il résulte

ou

L'expérience montre que T ¥ Þ wl ¥. Ceci implique que B12 = B21. Alors

Pour obtenir la vraie expression de la densité spectrale d'énergie il suffit seulement que
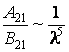
ce qui a été démontré dans la mécanique quantique.
Il y a deux modÈles différents des rayonnements lumineux: le modÈle ondulatoire et le modÈle corpusculaire. Certains phénomÈnes lumineux peuvent Être expliqués en utilisant toutes les deux théories (par exemple, la réflexion, la réfraction, certaines des lois du rayonnement thermique). D'autres phénomÈnes lumineux peuvent Être expliqués seulement en utilisant le modÈle ondulatoire (par exemple, l'interférence, la diffraction, la polarisation). Enfin, il y a des phénomÈnes qui ne peuvent Être expliqués qu'en utilisant la théorie photonique (par exemple, l'effet photoélectrique, l'effet de Compton, la loi de la distribution spectrale de l'énergie rayonnante du corps noir).
Cette réalité nous fait à soutenir que la lumiÈre est, au niveau de modÈle, un dualisme corpuscule-onde, en dépit du fait que les concepts impliqués sont contradictoires. En fond, ces deux concepts sont seulement des hypothÈses utilisées pour simplifier les choses, qui exposent une facette ou l'autre d'une réalité physique qui est beaucoup plus complexe. Dans ce contexte, il pourrait Être intéressant de remarquer que le mÊme rayonnement peut manifester tant de propriétés ondulatoires que de propriétés corpusculaires, en fonction du processus auquel il est part (ainsi, la lumiÈre visible se comporte comme une onde dans le phénomÈne d'interférence, mais elle se manifeste comme un flux de corpuscules dans le cas de l'effet photoélectrique). On peut affirmer que le comportement ondulatoire est probable quand l'énergie lumineuse est petite par comparaison à l'énergie caractéristique au phénomÈne étudié (par exemple, si l'énergie du photon hc/l est petite par comparaison à l'énergie caractéristique d'agitation thermique, alors le rayonnement thermique peut Être considéré de nature ondulatoire, limite dans laquelle la loi de Planck correspond à la loi de Rayleigh-Jeans). Le comportement corpusculaire se retrouve dans le cas contraire (par exemple, quand l'énergie du photon est comparable au travail d'extraction dans le cas de l'effet photoélectrique).
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1281
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved