| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
On va examiner en suite un exemple facile d'utilisation de l'équation stationnaire de Schrödinger pour déterminer l'expression de la fonction d'onde.
|
|
On va considérer une microparticule située dans une région de l'espace de longueur l, oÙ son énergie potentielle est nulle. En dehors de cette région, l'énergie potentielle est infinie. La particule peut se déplacer seulement au long de l'axe Ox. Un tel type de distribution de l'énergie potentielle s'appelle puits de potentiel infini unidimensionnel.
Puisque la hauteur du puits de potentiel est infinie, la probabilité de trouver la particule en dehors du puits est nulle. Il résulte
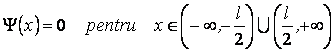
À l'intérieur du puits, l'énergie potentielle de la particule est nulle, ainsi que l'équation stationnaire de Schrödinger est
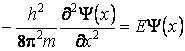
On peut mettre l'équation sous la forme
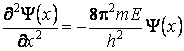
Il y a trois situations possibles:
Þ
![]()
Avec
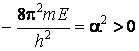
la solution générale de l'équation différentielle est
![]()
la fonction d'onde doit Être continue dans les points x = l/2, ainsi que
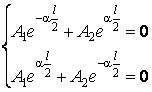
La solution du systÈme est A1 = A2 = 0, c'est-à-dire Y(x) = 0, solution sans sens physique.
Þ E
dans ce cas on obtien aussi une solution sans sens physique Y(x) = 0.
Þ
![]()
Avec
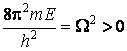
l'équation différentielle
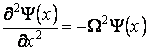
a la solution générale
![]()
oÙ A et j sont deux constantes d'intégration. La fonction d'onde doit Être continue dans les points x = l/2, ainsi que
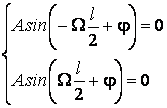
Puisque l'amplitude A ne peut pas Être nulle, les solutions du systÈme sont
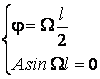
De la deuxiÈme équation on obtient
![]()
ou
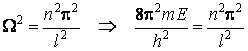
ou
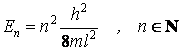
c'est-à-dire les valeurs propres de l'énergie de la particule sont quantifiées (ou, autrement dit, l'énergie de la particule ne peut pas avoir que de valeurs discrÈtes).
En introduisant les valeurs de W et j dans la solution générale de l'équation différentielle, on obtient
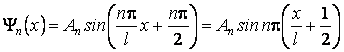
Puisque la fonction d'onde doit Être normée, il résulte

On obtient
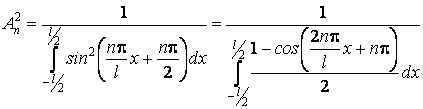
ou
![]()
La résolution de l'équation de Schrödinger est finalisée à cet instant. Les fonctions propres ont les expressions

L'état fondamental du systÈme physique correspond à l'énergie minimum, respectivement à la valeur minimum du nombre quantique n: n = 1. La valeur de l'énergie du niveau fondamental est
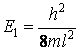
et l'énergie d'un niveau supérieur est
![]()
La densité de probabilité de la présence de la particule dans un point du puits de potentiel est donnée par le module carré de la fonction d'onde
|
|
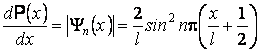
Le graphique de la densité de probabilité de la présence de la particule dans un point du puits de potentiel montre que celle-ci n'est pas uniformément distribuée. La localisation de la particule semble a une onde stationnaire (les points de probabilité maximum correspondant aux ventres de l'onde stationnaire, est ceux de minimum aux noeuds). Dans la mécanique classique, la particule pourrait occuper avec la mÊme probabilité n'importe quel point du puits de potentiel, en résultant une valeur constante pour la densité de probabilité
![]()
On observe que la densité quantique de probabilité atteint dans certains points une valeur double par rapport à la probabilité classique, mais il y a aussi des points ou elle s'annule. Si on observe de plus que la densité quantique de probabilité peut Être écrite comme
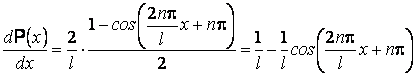
il résulte
que la situation classique est la limite de la solution quantique dans le cas
oÙ la moyenne du terme 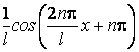 est nulle sur une distance Dx arbitrairement
petite, autour le point considéré. Ceci veut dire que le terme
est nulle sur une distance Dx arbitrairement
petite, autour le point considéré. Ceci veut dire que le terme ![]() représente un relativement grand nombre de
périodes de la fonction trigonométrique
représente un relativement grand nombre de
périodes de la fonction trigonométrique
![]()
De la
![]()
Comme ![]() , il
résulte
, il
résulte
![]()
c'est-à-dire le comportement quantique de la particule se confond avec le comportement classique quand la valeur du nombre quantique est trÈs grande. Cette affirmation équivaut à soutenir que la mécanique classique est valide seulement pour les particules qui ont des énergies beaucoup plus grandes que l'énergie de l'état fondamental, respectivement l'énergie caractéristique du processus dont elles font partie.
On avait déjà montré que dans la mécanique quantique, quand les valeurs propres de l'énergie sont discrÈtes, l'énergie de la particule peut varier seulement par sauts. Dans notre cas
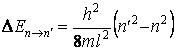
Dans la mécanique classique, l'énergie peut varier d'une maniÈre continue. Du point de vue des mathématiques, ceci signifie que la variation relative d'énergie peut tendre à zéro
![]()
La variation minimum d'énergie dans le cas quantique correspond à l'augmentation du nombre quantique avec une unité. Dans cette situation, la variation relative d'énergie est
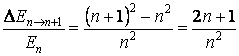
L'analyse de cette expression confirme une fois de plus que l'approximation classique correspond aux grandes valeurs du nombre quantique, quand
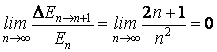
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1639
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved