| CATEGORII DOCUMENTE |
| Aeronautica | Comunicatii | Electronica electricitate | Merceologie | Tehnica mecanica |
ASAMBLARI ELASTICE (ARCURI)
Definire, clasificare, domenii de folosire
Arcurile sunt organe de masini care realizeaza o legatura elastica intre anumite piese sau subansamble ale unei masini. Prin forma lor si prin caracteristicile mecanice deosebite ale materialelor din care se confectioneaza, arcurile au capacitatea de a se deforma sub actiunea unei forte exterioare, preluand lucrul mecanic al acesteia si inmagazinandu-l sub forma de energie de deformatie. La disparitia sarcinii exterioare, energia inmagazinata este restituita sistemului mecanic din care face parte arcul.
Clasificarea arcurilor se face dupa o serie de criterii, prezentate in continuare.
Dupa forma constructiva, se deosebesc: arcuri elicoidale, arcuri bara de torsiune, arcuri spirale plane, arcuri in foi, arcuri inelare, arcuri disc si arcuri bloc.
Dupa modul de actionare a sarcinii exterioare, clasificarea se face in: arcuri de compresiune, arcuri de tractiune, arcuri de torsiune si arcuri de incovoiere.
Dupa solicitarea principala a materialului, se deosebesc arcuri solicitate la torsiune, la incovoiere si la tractiune-compresiune.
Dupa natura materialului din care este executat arcul, se deosebesc arcuri metalice si arcuri nemetalice.
Dupa variatia rigiditatii, arcurile pot fi cu rigiditate constanta sau cu rigiditate variabila (progresiva sau regresiva).
Dupa forma sectiunii arcului, se deosebesc arcuri cu sectiune circulara, inelara, dreptunghiulara, profilata sau compusa.
Domeniile de folosire ale arcurilor sunt variate, cele mai importante fiind:
amortizarea socurilor si vibratiilor (la suspensiile autovehiculelor, cuplaje elastice, fundatia utilajelor etc.);
acumularea de energie (la ceasuri cu arc, arcurile supapelor etc.), care apoi poate fi restituita treptat sau brusc;
exercitarea unei forte permanente, elastice (la cuplajele de siguranta prin frictiune, ambreiaje prin frictiune etc.);
reglarea sau limitarea fortelor (la prese, robinete de reglare etc.);
masurarea fortelor si momentelor, prin utilizarea dependentei dintre sarcina exterioara si deformatia arcului (la cantare, chei dinamometrice, standuri de incercare etc.);
modificarea frecventei proprii a unor sisteme mecanice.
Materiale si tehnologie
Materialele utilizate in constructia arcurilor se aleg astfel incat sa indeplineasca o serie de conditii generale, cum sunt: rezistenta ridicata la rupere, limita ridicata de elasticitate, rezistenta mare la oboseala (uneori si rezistenta la temperaturi inalte, rezistenta la coroziune, lipsa proprietatilor magnetice, dilatatie termica redusa, comportare elastica independenta de temperatura etc.).
Materialele feroase dedicate constructiei arcurilor sunt otelurile. Acestea pot fi oteluri carbon de calitate (OLC 55A, OLC 65A, OLC 75A, OLC 85A) sau oteluri aliate (cu Si, pentru rezistenta si tenacitate; cu Mn sau Cr, pentru calibilitate si rezistenta la rupere; cu V, pentru rezistenta la oboseala; cu Ni, pentru termorezistenta). Otelurilor pentru arcuri li se aplica un tratament termic de calire si revenire medie, obtinandu-se in acest mod o elasticitate marita in toata masa materialului. Marcile de oteluri pentru arcuri sunt standardizate.
Materialele neferoase se folosesc, de regula, la arcuri care lucreaza in campuri electrostatice, pentru care se doreste lipsa proprietatilor magnetice. Cele mai utilizate materiale neferoase pentru arcuri sunt alama si bronzul, dar si anumite aliaje speciale (Monel, Inconel etc.).
Materialele nemetalice utilizate la arcuri sunt cauciucul, pluta etc.
Tehnologia de obtinere a arcurilor depinde, cu precadere, de forma constructiva a acestora.
Semifabricatele pentru arcuri elicoidale se prezinta sub forma de sarme, bare, benzi etc.. Forma elicoidala se obtine prin infasurare la rece (la arcuri cu sectiune mica) sau prin infasurare la cald (la arcuri cu sectiune mai mare). Tratamentul termic se efectueaza, in general, dupa infasurare. La arcuri infasurate la rece, putin solicitate, tratamentul termic se poate face inainte de infasurare, urmand ca dupa infasurare sa se efectueze doar operatii de revenire.
Calitatea suprafetei arcurilor este determinanta pentru rezistenta acestora la oboseala. In scopul cresterii durabilitatii arcurilor supuse la solicitari variabile, masurile care se iau sunt: rectificarea suprafetei arcului (dupa tratamentul termic), durificarea stratului superficial (daca nu este posibila rectificarea), acoperirea suprafetei (pentru protectie impotriva coroziunii), evitarea decarburarii suprafetelor in timpul tratamentului termic etc.
3. CARACTERISTICA ELASTICA
Caracteristica elastica a unui arc reprezinta dependenta dintre sarcina exterioara ( forta sau moment de torsiune) care actioneaza asupra sa si deformatia elastica (sageata sau rotire) pe directia sarcinii. In functie de tipul sarcinii exterioare, caracteristica elastica se poate exprima prin una din expresiile F = F(δ) sau Mt = Mt(θ), in care δ reprezinta deformatia liniara a arcului pe directia fortei F (sageata), iar θ - deformatia unghiulara a arcului pe directia momentului de torsiune Mt (rotirea). In fig. 1 sunt prezentate cele doua tipuri de caracteristici elastice liniare corespunzatoare celor doua tipuri de sarcini exterioare.
Panta caracteristicii elastice a arcului indica rigiditatea c a arcului, care se detrmina cu una din relatiile (v. fig. 1):
![]()
![]()
|
a b Fig. 1 Caracteristici elastice liniare |
Caracteristica elastica liniara este intalnita doar la arcuri care lucreaza fara frecare, executate din materiale care respecta legea lui Hooke. Aceste arcuri sunt caracterizate de rigiditate constanta c = const.
O alta marime care caracterizeaza functionarea unui arc este energia de deformatie acumulata, egala, in absenta frecarilor, cu lucrul mecanic al fortei care a provocat deformatia. In fig. 1, suprafetele hasurate reprezinta lucrul mecanic de deformatie al arcului incarcat cu forta F3 (v. fig. 1,a), respectiv cu momentul de torsiune Mt3 (v. fig.1,b). Expresiile lucrului mecanic de deformatie sunt:
![]() respectiv
respectiv ![]()
|
Fig. 2 Caracteristici elastice neliniare |
Desi arcurile cu caracteristica elastica liniara (rigiditate constanta) sunt cele mai intalnite, in practica se utilizeaza si arcuri cu rigiditate variabila, la care caracteristica elastica este neliniara (fig. 2).
Rigiditatea acestor arcuri se exprima prin una din relatiile:
![]()
![]()
Caracteristicile cu rigiditate progresiva au panta crescatoare, iar caracteristicile cu rigiditate regresiva au panta descrescatoare.
Lucrul mecanic de deformatie al arcurilor cu caracteristica elastica neliniara se exprima sub una din formele (v. fig. 2):
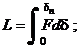
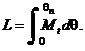
Caracteristica elastica la descarcare se suprapune exact peste caracteristica elastica de la incarcare doar daca nu exista frecari intre elementele componente.
|
Caracteristica teoretica Fig. 3 Caracteristica elastica cu "histerezis |
Daca arcurile sunt realizate din mai multe elemente suprapuse (arcuri in foi, arcuri inelare, arcuri disc) sau daca arcul este realizat dintr-un material cu frecari interne considerabile (arcuri din cauciuc), caracteristica elastica (fig.3.3) prezinta o diferenta intre incarcare si descarcare (asa-numitul "histerezis").Lucrul mecanic absorbit de arc in timpul incarcarii (suprafata de sub caracteristica de incarcare) este diferit de lucrul mecanic cedat de arc in timpul descarcarii (suprafata de sub caracteristica de descarcare). Diferenta dintre aceste lucruri mecanice o reprezinta lucrul mecanic consumat prin frecare (suprata inchisa de bucla "histerezisului"), care se transforma in caldura si incalzeste arcul. Datorita acestui fenomen, arcurile care prezinta o caracteristica elastica cu "histerezis" au capacitate mai mare de amortizare a socurilor si vibratiilor.
ARCURI ELICOIDALE
Arcurile elicoidale se obtin din sarme sau bare de diverse profile, infasurate pe o suprafata directoare.
Arcurile elicoidale se clasifica dupa o serie de criterii, prezentate in continuare.
Dupa forma sectiunii spirei, arcurile elicoidale pot fi cu sectiune rotunda, cu sectiune patrata sau dreptunghiulara, cu sectiune profilata;
Dupa forma suprafetei directoare, arcurile elicoidale se impart in arcuri cilindrice, arcuri conice, arcuri dublu conice, paraboloidale, hiperboloidale, prismatice etc.
|
a b c d
e f Fig. 4 Arcuri elicoidale |
Dupa modul de actionare a sarcinii, se deosebesc arcuri elicoidale de compresiune, de tractiune si de torsiune.
Standardele reglementeaza, pentru arcuri elicoidale, clasificarea, terminologia si reprezentarea in desenul tehnic.
4.1. Arcuri elicoidale cilindrice de compresiune
In fig. 4 sunt prezentate cateva solutii de arcuri elicoidale de compresiune, iar in fig.5 sunt prezentate elementele geometrice ale arcurilor cilindrice elicoidale de compresiune cu sectiunea spirei rotunda (fig. 5, a) si dreptunghiulara (fig. 5, b).
|
a b c Fig. 5 Arcuri elicoidale cilindrice de compresiune. Elemente geometrice |
Terminologia utilizata pentru arcurile elicoidale cilindrice de compresiune cu sectiunea spirei rotunda (aplicabila si la sectiune dreptunghiulara a spirei) este:
d - diametrul spirei;
Di - diametrul interior de infasurare;
Dm - diametrul mediu de infasurare;
D - diametrul exterior de infasurare;
t - pasul spirei;
H - lungimea arcului in stare libera;
a - unghiul de inclinare al spirei in stare libera.
Suprafetele de asezare ale arcurilor elicoidale de compresiune se prelucreaza plan, perpendicular pe axa arcului. Spirele de capat, prelucrate astfel, nu se deformeaza elastic.
Numarul total de spire, nt , ale unui arc elicoidal de compresiune se determina cu relatia nt = n + nr , in care n reprezinta numarul de spire active (care participa la deformatia elastica a arcului), iar nr este numarul de spire de reazem (de capat), reglementat in standarde in functie de numarul de spire active: nr = 1,5, daca n 7; nr = 1,53,5, daca n > 7.
Calculul de rezistenta al arcului elicoidal cilindric de compresiune
|
Fig. 6 Schema pentru calculul de rezistenta al arcului elicoidal cilindric de compresiune cu spira rotunda |
|
Fig. 7 Distributia de tensiuni tangentiale pe spira arcului elicoidal |
Schema de calcul a arcului elicoidal cilindric de compresiune cu sectiunea spirei rotunda este prezentata in fig. 6. Forta F, care actioneaza in axa arcului, se descompune in doua componente:
F cosa
- perpendiculara pe planul spirei - determina solicitarile de torsiune (data
de momentul de torsiune ![]() )
si de forfecare (data de forta taietoare T = F
cosa
)
si de forfecare (data de forta taietoare T = F
cosa
F sina -
aflata in planul spirei - determina solicitarile de incovoiere
(data de momentul de incovoiere ![]() )
si de compresiune (data de forta normala N =
F cosa
)
si de compresiune (data de forta normala N =
F cosa
Deoarece
unghiul de inclinare a spirei are valori mici (a = 6.9 o), deci cosa 1 si sin a 0, iar tensiunea de forfecare este
neglijabila, in calcule se considera doar solicitarea de torsiune, cu
momentul ![]() .
.
Tensiunea de torsiune care apare in spira arcului - considerata de forma unei bare drepte - este
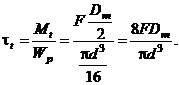
Notand cu ![]() indicele arcului, relatia tensiunii de
torsiune poate fi scrisa sub forma
indicele arcului, relatia tensiunii de
torsiune poate fi scrisa sub forma ![]()
Deoarece distributia tensiunii de torsiune nu este uniforma pe circumferinta spirei, avand valori mai mari pe partea de la interiorul curburii (fig. 7), verificarea arcului la solicitarea de torsiune se efectueaza cu una din relatiile
![]() si
si ![]()
in care k reprezinta coeficientul de forma al arcului, dependent de indicele i al arcului si se poate determina cu relatia
![]()
Pentru dimensionarea spirei arcului rezulta:
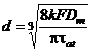 sau
sau 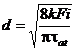 .
.
Rezistentele admisibile la torsiune tat se aleg [5, 14] in functie de materialul arcului, tratamentul termic aplicat, caracterul sarcinii (statica sau oscilanta), conditiile de functionare, importanta arcului in cadrul ansamblului din care face parte, luand valori in intervalul tat = 500.800 MPa.
Calculul la deformatii al arcului elicoidal cilindric de compresiune
Calculul la deformatii (denumit si calcul de rigiditate) este un calcul specific arcurilor si consta in determinarea deformatiei arcului corespunzatoare unei anumite incarcari.
|
Fig. 8 Schema de calcul la deformatii a arcului elicoidal cilindric de compresiune |
Deformatia arcului elicoidal cilindric de compresiune (sageata) este reprezentata de deplasarea punctului de aplicatie al fortei care il incarca, pe directia acesteia. Prin desfasurarea spirei arcului sub forma unei bare (fig. 8)
de lungime l = pDmn, deformatia este data de lungimea arcului de cerc de-a lungul caruia se deplaseaza forta F. Rasucirea totala a spirei arcului este
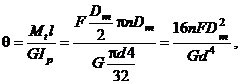
iar deformatia arcului este
![]() sau
sau ![]()
unde: n reprezinta numarul de spire active, G - modulul de elasticitate transversal si Ip - momentul de inertie polar al sectiunii spirei arcului.
Relatia de determinare a sagetii demonstreaza rolul determinant al indicelui arcului asupra elasticitatii acestuia. Arcurile cu indice mare sunt elastice (usor deformabile), iar cele cu indice mic sunt rigide.
Caracteristica elastica
|
Fig. 9 Caracteristica elastica a arcului elicoidal cilindric de compresiune |
In fig. 9 este prezentata caracteristica elastica a unui arc elicoidal cilindric de compresiune. Notatiile folosite in definirea acesteia sunt:
H - lungimea arcului in stare libera;
F - sarcina initiala, de precomprimare (de montaj);
d , H1 - sageata, respectiv lungimea arcului montat, pretensionat cu forta F1;
Fmax - sarcina maxima de functionare;
dmax, Hmax - sageata, respectiv lungimea arcului sub actiunea fortei Fmax;
h - cursa de lucru a arcului;
Fb - sarcina limita de blocare a arcului;
db, Hb - sageata, respectiv lungimea arcului blocat (comprimat spira pe spira).
Datorita neuniformitatii pasului spirelor, la incarcare, unele spire intra in contact mai repede decat altele si, in consecinta, portiunea finala a caracteristicii devine progresiva. Pentru evitarea functionarii pe aceasta portiune neliniara a caracteristicii se recomanda limitarea sarcinii maxime de functionare Fmax .0,9) Fb.
Algoritm de proiectare
Dimensionarea unui arc elicoidal cilindric de compresiune se efectueaza atat prin adoptarea unor parametri geometrici si functionali ai acestuia, din considerente tehnologice si functionale, cat si in urma calculelor de rezistenta si la deformatii.
Datele de intrare generale sunt: forma sectiunii spirei, sarcina maxima care incarca arcul, sageata maxima sau numarul de spire active sau rigiditatea impusa si conditiile de functionare.
Etapele de proiectare ale unui arc elicoidal cilindric de compresiune sunt prezentate in continuare.
Se alege materialul arcului in functie de conditiile de functionare si se stabileste rezistenta admisibila la torsiune.
Se efectueaza calculul de rezistenta, in urma caruia se determina diametrul d al spirei, care trebuie sa corespunda unei sarme standardizate.
Se efectueaza calculul la deformatii - alegandu-se sau adoptandu-se numarul de spire active - astfel incat arcul sa asigure conditiile de rigiditate si de gabarit impuse.
Se stabilesc dimensiunile geometrice ale arcului si parametrii corespunzatori caracteristicii elastice.
Se intocmeste desenul de executie, in conformitate cu rezultatele etapelor anterioare si cu prescriptiile cuprinse in standarde.
4.2. Arcuri elicoidale cilindrice de tractiune
Arcul elicoidal de tractiune preia o sarcina axiala care tinde sa il intinda. Sarcina se aplica prin intermediul unor ochiuri de prindere, de forma unor carlige realizate prin deformarea spirelor de capat ale arcului (fig. 10, a, b, c si d) sau prin intermediul unor piese separate (fig. 10, e si f).
Spira arcului elicoidal de tractiune este solicitata, in principal, la torsiune la fel ca spira arcului elicoidal de compresiune. Calculul de rezistenta al arcului elicoidal de tractiune se efectueaza pe baza relatiilor prezentate in subcap. 4.
In calculul arcurilor elicoidale de tractiune se recomanda sa se lucreze cu rezistente admisibile micsorate cu 12% fata de cele utilizate la calculul arcurilor elicoidale de compresiune.
Calculul la deformatii se bazeaza pe relatiile stabilite in subcap. 4, pentru arcul elicoidal cilindric de compresiune.
|
a b c d
e f Fig. 10 Sisteme de prindere a arcurilor cilindrice elicoidale de tractiune |
Teoretic, arcurile elicoidale cilindrice de tractiune au caracteristica elastica liniara, identica cu a arcurilor elicoidale cilindrice de compresiune (v. fig. 9). Practic, arcurile elicoidale de tractiune se realizeaza, de regula, cu spirele infasurate strans. Prin aceasta, spirele nu numai ca sunt in contact in stare libera, dar sunt si apasate reciproc, datorita unei forte initiale de pretensionare. Caracteristica elastica a acestor arcuri si parametrii care o definesc sunt prezentate in fig. 11. Notatiile utilizate sunt:
|
Fig. 11 Caracteristica elastica a arcului elicoidal cilindric de tractiune |
HC - inaltimile ochiurilor de prindere;
H - lungimea activa a arcului in stare libera;
H - lungimea arcului in stare libera;
F - forta de montaj;
d , H1 - sageata, respectiv lungimea arcului montat, incarcat cu forta F1;
Fmax - sarcina maxima de functionare;
dmax, Hmax - sageata, respectiv lungimea arcului sub actiunea fortei Fmax;
h - cursa de lucru a arcului;
Flim - sarcina limita de incarcare, sub actiunea careia tensiunile din arc se apropie de limita de curgere a materialului;
Hlim - lungimea arcului sub actiunea fortei Flim, deformatiile ulterioare impunandu-se a fi limitate prin limitatoare speciale.
Datorita imperfectiunilor de montaj, apasarea initiala dintre spire nu este uniforma. Ca urmare, la inceputul incarcarii, caracteristica elastica nu este liniara (urmareste linia intrerupta din fig. 11).
Arcuri elicoidale cilindrice de torsiune
|
Fig. 12 Arc elicoidal cilindric de torsiune |
Arcurile elicoidale cilindrice de torsiune preiau un moment de torsiune aplicat pe directia axei arcului. Forma acestor arcuri este asemanatoare cu a arcurilor elicoidale cilindrice de compresiune, diferenta fiind data de constructia spirelor de capat, indoite astfel incat sa permita fixarea la un capat si aplicarea momentului de torsiune la celalalt capat.
In fig. 12 este prezentata o schema a arcului elicoidal cilindric de torsiune, din care se observa incarcarea realizata prin aplicarea unei forte F cu bratul R. In urma incarcarii cu momentul de torsiune Mt = FR, capatul activ al arcului se roteste cu unghiul q
Calculul de rezistenta
Asupra spirei arcului actioneaza momentul de torsiune Mt, care se descompune in doua componente (fig. 13):
Mt cosa - perpendiculara pe planul spirei - determina solicitarea de incovoiere a spirei;
|
Fig. 13 Schema pentru calculul de rezistenta |
Mt sina - aflata in planul spirei determina solicitarea de torsiune.
Deoarece unghiul de inclinare a a spirei arcului are valori mici (cosa 1 si sina 0), in calculul de rezistenta se ia in considerare doar solicitarea de incovoiere.
Calculul de verificare a spirei la incovoiere se efectueaza cu relatia
![]()
in care: ki este coeficientul de corectie a tensiunii de
incovoiere, se alege in functie de indicele arcului ![]() si tine
seama de faptul ca distributia tensiunii de incovoiere este
influentata de curbura spirei, tensiunea maxima de incovoiere
aparand in partea interioara a spirei; sai - rezistenta admisibila la incovoiere, se
stabileste in functie de rezistenta admisibila la torsiune sai tat
si tine
seama de faptul ca distributia tensiunii de incovoiere este
influentata de curbura spirei, tensiunea maxima de incovoiere
aparand in partea interioara a spirei; sai - rezistenta admisibila la incovoiere, se
stabileste in functie de rezistenta admisibila la torsiune sai tat
Prin prelucrarea relatiei, rezulta relatia de dimensionare a spirei arcului elicoidal cilindric de torsiune
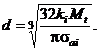
Calculul la deformatii
|
Fig. 14 Schema de calcul la deformatii a arcului elicoidal cilindric de torsiune |
Deformatia arcului se determina corespunzator barei drepte - de lungime l = npDm - obtinuta prin desfasurarea spirei arcului, incastrata la un capat si incarcata cu un moment de incovoiere Mi = Mt = FR (fig. 14).
Relatia de calcul a unghiului de rotire a arcului este
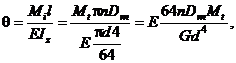
unde n reprezinta numarul de spire active, E - modulul de elasticitate longitudinal al materialului arcului si Iz - momentul de inertie axial al sectiunii spirei arcului.
5. ARCUL BARA DE TORSIUNE
Definire, caracterizare
Arcul bara de torsiune este, asa cum ii arata numele, de forma unei bare incarcata cu un moment de torsiune. Constructiv, arcul se poate prezenta sub aspectul unei bare incastrate la un capat, incarcata cu o forta aplicata prin intermediul unui levier la celalalt capat (fig. 15, a) sau ca o bara libera, incarcata la ambele capete cu forte, prin intermediul unor leviere (fig. 15, b). Pentru evitarea solicitarii de incovoiere, bara se monteaza pe lagare cu alunecare amplasate cat mai aproape de levierele de actionare.
|
a b Fig. 15 Arcuri bara de torsiune |
 Sectiunea arcului poate fi rotunda (fig.
16, a), inelara, patrata, dreptunghiulara (fig. 16, b),
hexagonala, compusa din mai multe bare rotunde (fig. 16, c) sau
dintr-un pachet de lamele (fig. 16, d). Cel mai frecvent se intalnesc barele cu
sectiune rotunda, care asigura uniformitatea distributiei
tensiunii tangentiale si simplitate tehnologica.
Sectiunea arcului poate fi rotunda (fig.
16, a), inelara, patrata, dreptunghiulara (fig. 16, b),
hexagonala, compusa din mai multe bare rotunde (fig. 16, c) sau
dintr-un pachet de lamele (fig. 16, d). Cel mai frecvent se intalnesc barele cu
sectiune rotunda, care asigura uniformitatea distributiei
tensiunii tangentiale si simplitate tehnologica.
Avantajele arcurilor bara de torsiune sunt:
dimensiuni de gabarit reduse;
constructie simpla;
montaj si intretinere usoara;
lipsa frecarilor interioare;
tehnologie de executie relativ simpla;
Arcurile bara de torsiune se utilizeaza la suspensia autovehiculelor, cuplaje elastice, chei dinamometrice, aparate de masura, instalatii de incarcare a standurilor de incercare etc
Calculul de rezistenta al arcurilor bara de torsiune de sectiune circulara se efectueaza la solicitarea de torsiune, conform schemei de calcul prezentate in fig. 17. Relatia de verificare la torsiune este
|
Fig. 17 Schema de calcul a arcului bara de torsiune |
![]()
in care momentul de torsiune se determina in functie de forta F si bratul a la care este aplicata pe levier Mt = Fa.
Din relatia tensiunii de torsiune se obtine relatia de dimensionare a arcului bara de torsiune
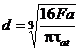 .
.
Rezistenta admisibila la torsiune se alege in functie de materialul arcului, caracterul solicitarii (statica sau variabila), diametrul barei si starea suprafetei acesteia, luand valori in intervalul tat = 500.800 MPa.
Calculul la deformatii (v. fig. 17) se efectueaza pe baza relatiei
![]()
in care: l reprezinta lungimea de lucru a barei, G - modulul de elasticitate transversal al materialului arcului, Ip - momentul de inertie polar al sectiunii arcului.
Daca deformatia este impusa, se poate determina lungimea necesara a arcului
![]()
Conform relatiei (3.21), caracteristica elastica a arcului bara de torsiune este liniara (v. fig. 3.2).
Elemente constructive
|
Fig. 1 Elemente constructive ale arcurilor bara de torsiune |
Capetele de incastrare si cele pe care se asambleaza levierele se pot realiza cu aplatisare, dc = 1,6d si d1 = 1,2d (fig. 18, a), cu contur hexagonal (fig. 18, b), cu contur patrat (fig. 18, c), canelate (fig. .18, d) etc. Intre portiunea de lucru - cu diametrul d - si capetele barei, se prevad raze de racordare mari (r 2d), astfel incat sa se micsoreze concentratorul de tensiune si sa se mareasca rezistenta la oboseala. In acelasi scop, suprafata barei se rectifica si se acorda o atentie deosebita tratamentului termic.
6. ARCURI SPIRALE PLANE
|
Fig. 19 Arcul spiral plan |
Arcurile spirale plane preiau momente de torsiune, numele lor venind de la faptul ca banda din otel de arc, din care sunt confectionate, este infasurata dupa o spirala arhimedica (fig. 19). Asemanator cu constructia arcului elicoidal de torsiune, un capat este fixat, iar la capatul opus se aplica momentul de torsiune. In fig. 19 s-a notat cu: 1 - arcul spiral plan, 2 - arborele de incarcare prin intermediul caruia se aplica momentul de torsiune Mt, 3 - carcasa in care se incastreaza capatul exterior al arcului.
Arcul spiral plan se utilizeaza, in principal, ca element motor, avand capacitate mare de deformatie si de inmagazinare de energie - la armare - energie pe care o poate ceda ulterior, in timp. Este intalnit, cu precadere, la mecanisme de ceas si aparate de masura.
Calculul de rezistenta se
efectueaza la solicitarea de incovoiere, momentul de incovoiere care
solicita spira arcului fiind egal cu momentul de torsiune preluat de
catre arc Mi =
![]()
unde: b reprezinta latimea benzii, h - grosimea benzii, sai - rezistenta admisibila la incovoiere a materialului arcului.
Relatia de mai sus poate fi rescrisa, pentru dimensionarea arcului, sub forma
![]()
Grosimea h a benzii se poate adopta in functie de diametrul d al arborelui de incarcare h = (0,003.0,004) d.
Calculul la deformatii se efectueaza cu relatia
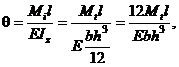
in care: l reprezinta lungimea arcului, E - modulul de elasticitate longitudinal al materialului arcului; Iz - momentul de inertie axial al sectiunii spirei arcului. Relatia de deformatii a fost obtinuta prin asimilarea arcului spiral plan, prin desfasurare, cu o bara incastrata, incarcata cu un moment de incovoiere Mi = Mt - similar schemei de calcul la deformatii a arcului cilindric de torsiune (v. fig. 14) - rotirea la capatul barei fiind aceeasi cu unghiul de rotire al arborelui de incarcare a arcului spiral plan. Din relatia de deformatii rezulta liniaritatea caracteristicii elastice a arcului spiral plan.
ARCURI LAMELARE
Arcurile lamelare se prezinta in doua forme constructive principale: formate dintr-o singura lamela si formate din mai multe lamele suprapuse (arcuri in foi multiple).
7.1. Arcuri monolamelare
Arcurile monolamelare se regasesc, de
regula, sub forma de lamela incastrata la un capat si libera la celalalt
capat. Se utilizeaza ca arcuri de apasare, in
constructia instrumentelor de masurare, la mecanisme cu clichet,
mecanisme de zavorare etc. Sectiunea lamelei este
dreptunghiulara, cu grosimea h, de regula,
|
a
b
c
d Fig. 20 Forme constructive de arcuri monolamelare |
Calculul de rezistenta
consta in limitarea tensiunii de incovoiere, maxima in
sectiunea de incastrare a lamelei, 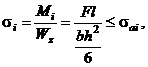
unde l reprezinta lungimea activa a lamelei.
Relatia poate fi rescrisa, pentru determinarea latimii necesare a lamelei, sub forma
![]()
grosimea h a lamelei adoptandu-se din considerente constructive.
Calculul la deformatii urmareste determinarea dependentei sagetii d la capatul liber al arcului lamelar, sub actiunea fortei F. Relatia de calcul este
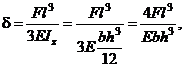
unde E reprezinta modulul de elasticitate longitudinal al materialului arcului. Conform acestei relatii, caracteristica elastica a arcului monolamelar este liniara.
7.2. Arcuri in foi
Arcurile in foi sunt compuse din mai multe arcuri lamelare suprapuse, de lungimi diferite, asamblate astfel incat toate sa participe la deformatie. Arcurile in foi sunt frecvent folosite la suspensia vehiculelor (rutiere si feroviare), in constructia amortizoarelor, instalatiilor de forjare, la tampoanele ascensoarelor etc.
In fig. 21 sunt prezentate cateva variante constructive uzuale: a - cu un singur brat (sfertul de arc); b - cu doua brate, cu preluarea sarcinii la mijlocul arcului (arc semieliptic); c - cu doua brate, cu preluarea sarcinii la un capat al arcului (arc cantilever); d - format din doua brate suprapuse (arc dublu sau eliptic). O varianta mai noua este cea prezentata in fig. 21, e, cu lamele cu grosime variabila, aceasta constructie reducand greutatea arcului cu cel putin 30 Prin separarea lamelelor cu garnituri din material plastic (v. fig. 21, e), frecarea dintre lamele se poate reduce cu 80
|
|
|
a b
c d
e Fig. 21 Forme constructive de arcuri in foi |
Frecarea dintre lamelele arcurilor cu foi este dorita, in special atunci cand arcul se utilizeaza ca element de amortizare. O parte din energia preluata de arc este transformata, prin frecare, in caldura si nu mai este restituita sistemului din care face parte arcul, dupa disparitia incarcarii. Daca sarcina exterioara actioneaza asupra arcului cu socuri mici, care nu inving frecarea din arc si nu il deformeaza, acestea se vor transmite integral sistemului din care face parte arcul. In aceste cazuri, frecarea are un efect nedorit.
Frecarea dintre foi depinde de o serie de elemente, cum sunt: calitatea suprafetelor in contact, starea de ungere a suprafetelor in contact, numarul si lungimea foilor.
Uneori, foile de arc se executa cu o curbura initiala, cu atat mai mare cu cat lungimea lor este mai mica, astfel incat sa se asigure participarea tuturor foilor la transmiterea sarcinii.
Calculul arcurilor in foi se efectueaza prin asimilarea acestora cu un arc monolamelar cu grosime variabila. Elementele de calcul ale arcurilor in foi sunt prezentate in literatura de specialitate, precizia calculului avand de suferit din cauza complexitatii fenomenelor intalnite.
ARCURI INELARE
|
|
a b
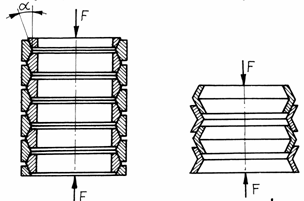
Fig. 22 Arcuri inelare
Arcurile inelare se obtin prin inserierea unor inele tronconice interioare sau exterioare, asamblate alternant, cu contact pe suprafretele conice (fig. 22). Arcurile inelare preiau o sarcina exterioara de compresiune, sub actiunea careia inelele interioare tind sa isi micsoreze diametrul, comprimandu-se, iar inelele exterioare tind sa isi mareasca diametrul, intinzandu-se. Intre inele apar forte de frecare mari, lucrul mecanic de frecare ajungand la 60.70% din lucrul mecanic al fortei exterioare, ceea ce conduce la capacitate mare de amortizare. Datorita acestei caracteristici, arcurile inelare se utilizeaza ca arcuri tampon, la preluarea unor sarcini foarte mari (la arcurile tampon de la materialul rulant). Unghiul a (v. fig. 22) al suprafetelor conice (a ) se alege astfel incat sa se evite intepenirea arcurilor si sa permita revenirea acestora la forma initiala, dupa incetarea actiunii sarcinii exterioare.
Pentru marirea elasticitatii arcului, inelele interioare si cele exterioare se pot realiza sub forma prezentata in fig. 22, b.
Inelele de dimensiuni mari se executa prin forjare, iar cele de dimensiuni mici prin matritare, suprafetele conice de contact prelucrandu-se prin aschiere.
ARCURI DISC
|
b |
c d
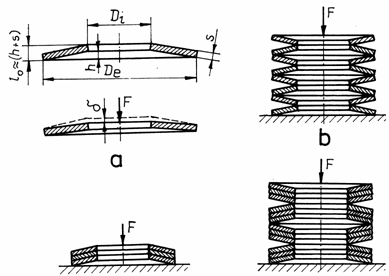
Fig. 23 Arcuri disc
Arcurile disc sunt formate din una sau mai multe placi inelare, de forma tronconica, fiind supuse la sarcini axiale de compresiune. Elementele geometrice ale arcului disc, prezentate in fig. 23, a, sunt:
Di - diametrul interior;
De - diametrul exterior;
s - grosimea placii;
h - inaltimea arcului.
Sub actiunea fortei exterioare F, arcul se deformeaza cu sageata d, in sensul micsorarii inaltimii h.
Conform prescriptiilor standar-dizate, compunerea arcurilor disc se poate realiza:
in coloana, prin asezarea alternanta a discurilor (fig. 23, b), marindu-se elasticitatea;
in pachete de discuri suprapuse pe aceeasi parte (fig. 23, c), rigiditatea obtinuta fiind mai mare si frecarile mai pronuntate;
in coloana de pachete (fig. 23, d), cu rigiditate intermediara celor doua moduri de compunere prezentate anterior.
Arcurile disc se utilizeaza ca arcuri tampon la instalatiile de matritat sau stantat, la fundatia masinilor grele, la tampoanele unor vehicule etc., acolo unde trebuiesc preluate socuri rare si mari sau sarcini statice foarte mari, cu deformatii relativ mici.
Discurile se obtin din tabla de otel de arc, prin stantare, bombare conica ( prin presare la cald), urmate de tratamentul termic.
Calculul arcurilor disc este
dificil, datorita complexitatii solicitarilor si
modificarii geometriei in timpul incarcarii. Metodica
de calcul presupune distributia uniforma a presiunii pe
circumferinta discurilor si considera invarianta geometria
arcului. Caracteristica elastica a arcului
disc este, in general, neliniara, depinzand de raportul ![]() si de modul de combinare a discurilor.
si de modul de combinare a discurilor.
ARCURI DIN CAUCIUC
Arcurile din cauciuc se utilizeaza datorita unor caracteristici particulare speciale, determinate de proprietatile cauciucului. Aceste caracteristici sunt: capacitate mare de amortizare, capacitate mare de deformare, constructie si tehnologie simple, functionare sigura si silentioasa, pret redus.
Capacitatea mare de amortizare a arcurilor din cauciuc se datoreaza frecarilor interne prin care se preia aproximativ 40% din lucrul mecanic al fortei exterioare. Aceasta poate duce la fenomenul nedorit de incalzire a arcului, ceea ce impune prevederea unor masuri suplimentare pentru evacuarea caldurii.
Arcurile din cauciuc se utilizeaza, in special, pentru amortizarea socurilor si vibratiilor, la suspensia vehiculelor sau instalatiilor, la compensarea erorilor din unele lanturi cinematice si la modificarea turatiei critice a unor sisteme mecanice.
Arcurile pot fi realizate sub forma de blocuri sau prevazute cu cavitati.
Arcurile bloc, prezentate in fig. 24, sunt realizate prin vulcanizarea cauciucului pe elemente metalice si pot fi folosite pentru preluarea de sarcini verticale si orizontale (solutiile constructive din fig. 24, a) sau numai pentru preluarea de sarcini verticale (solutiile constructive din fig. 24, b).
Arcurile cu cavitati sunt prevazute cu sisteme de centrare in structuri rigide (fig. 25), care sa impiedice deformatia transversala asimetrica a arcului.
|
|

a b
Fig. 24 Arcuri bloc din cauciuc

Fig. 25 Arcuri cave din cauciuc

Fig. 26 Arcuri din cauciuc vulcanizat intre elemente metalice
Alte forme de arcuri, realizate prin vulcanizare pe elemente metalice, sunt prezentate in fig. 26.
Calculul arcurilor din cauciuc este deosebit de dificil, datorita complexitatii fenomenelor care se petrec la deformarea cauciucului si formelor constructive extrem de diverse. Relatiile de calcul prezentate in literatura de specialitate sunt valabile doar pentru domeniul cvasiliniar al caracteristicii elastice a arcurilor.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 12387
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved