| CATEGORII DOCUMENTE |
| Agricultura | Asigurari | Comert | Confectii | Contabilitate | Contracte | Economie |
| Transporturi | Turism | Zootehnie |
| Navigatie |
NAVIGATIE AERIANA
1. GENERALITATI
Navigatia aeriana este stiinta care se ocupa cu metodele si practicile cele mai eficiente pentru asigurarea deplasarii aeronavelor in spatiul aerian in deplina siguranta a zborului
Pentru a se realiza deplasarea este necesara mentinerea aeronavei pe traiectul obligat si cunoasterea permanenta a pozitiei acesteia in spatiu, coordonate, directie de zbor, viteza, inaltime si timp calculat intre repere obligate.
In functie de felul zborului, a distantei, vitezei, inaltimii, a conditiilor meteo se foloseste una (sau mai multe) din metodele:
- metoda navigatiei observate consta in determinarea pozitiei aeronavei comparand reperele de pe sol cu semnele conventionale de pe harta;
- metoda navigatiei estimate consta in determinarea pozitiei aeronavei dupa diferite instrumente de la bord, efectuand unele calcule;
- metoda navigatiei radioelectrice consta in determinarea pozitiei aeronavei folosind mijloacele electronice ale aeronavei si/sau mijloace externe acesteia (amplasate pe sol sau sateliti);
- metoda navigatiei astronomice consta in determinarea pozitiei aeronavei dupa astrii de pe bolta cereasca cu ajutorul unor instrumente optice (de la bordul aeronavei);
- metoda navigatiei inertiale consta in determinarea pozitiei aeronavei (si a tuturor celorlalte elemente de zbor) plecand de la principiul determinarii acceleratiei ce ia nastere pe cele 3 axe ale aeronavei;
- metoda navigatiei izobarice consta in determinarea pozitiei aeronavei plecand de la diferenta indicatiilor de inaltime citite la altimetrul barometric si radioelectric.
Aviatia sportiva foloseste o metoda combinata si anume metoda observata impreuna cu cea estimata.
1.1. Globul pamantesc
Globul pamantesc are o forma complexa determinata de existenta muntilor si vailor. Aceasta forma se numeste geoid si se apropie de aceea a unui elipsoid obtinut prin rotirea unei elipse in jurul axei mici.
Dimensiunile pamantului sunt
urmatoarele:
- semiaxa mare = 6378,245 km
- semiaxa mica = 6356,86 km
- turtirea = (a-b)/b = 1/299
- volumul = 1082841315400 km3
- suprafata = 510100800 Km2 din care 29,4 % il reprezinta uscatul.
2. NOTIUNI GEOGRAFICE
Punctele si liniile de pe suprafata pamantului reprezinta elemente de referinta necesare efectuarii calculelor de navigatie.
Acestea se clasifica din doua puncte de vedere :
din punct de vedere geografic;
din punct de vedere al navigatiei aeriene.
Din punct de vedere geografic:
- axa terestra; este axa imaginara in jurul careia se invarteste pamantul;
- polii terestrii (geografici) sunt determinati de intersectia axei terestre cu suprafata pamantului.
Locul din care miscarea pamantului apare inversa acelor de ceasornic se numeste Polul nord. Opus lui este Polul sud.
- intersectia suprafetei pamantului cu un plan perpendicular pe axa terestra si care trece prin centrul pamantului este un cerc mare. Circumferinta acestui cerc mare se numeste ecuator.
Ecuatorul imparte pamantul in 2 emisfere: una nordica numita si boreala si o alta sudica numita australa.
- orice fel de cerc obtinut prin intersectia pamantului cu un plan ce nu trece prin centrul acestuia se numeste Cerc mic.
- Cercul mare care se obtine prin intersectia unui plan care contine si axa terestra se numeste Cerc meridia Semicercul mare ce trece prin punctul sau localitatea intersectata se numeste meridian geografic iar semicercul mare opus acestuia se numeste antimeridia
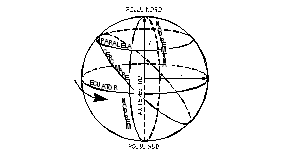
Fig. 2.1. Puncte si linii pe glob
- ca origine a unor masuratori in navigatia aeriana se foloseste Meridianul '0' (Meridianul Greenwich).
- cercurile mici de pe suprafata terestra paralele cu ecuatorul poarta denumirea de cercuri paralele sau Paralele.
- meridianele sunt numerotate incepand de la primul (Greenwich) spre est de la 0o la 180o si spre vest de la 0o la -180o.
- paralelele sunt notate in raport cu ecuatorul de la 0o la 90o N si de la 0o la 90o S.
In felul acesta orice punct de pe suprafata pamantului poate fi determinat ca fiind intersectia unei paralele cu un meridia
Din punct de vedere al navigatiei aeriene:
- de la aerodromul de plecare si pana la cel de destinatie o aeronava se deplaseaza de-a lungul unui itinerar, traiect sau ruta.
- punctul de la aerodromul de plecare sau de langa acesta (origine a masuratorilor si calculelor) se numeste Punct Initial al Traiectului (P.I.T.)
- punctul de la aerodromul de destinatie sau langa acesta (punctul final al masuratorilor) se numeste Punct Final al Traiectului (P.F.T.).
- linia ce marcheaza traiectul intre P.I.T. si P.F.T. si de-a lungul careia trebuie sa se deplaseze aeronava se numeste Linia Drumului Obligat (L.D.O.).
- linia care marcheaza traiectul de-a lungul caruia se deplaseaza in mod real o aeronava se numeste Linia Drumului Real (L.D.R.).
- unghiul format intre aceste 2 linii se numeste Abatere Laterala Unghiulara (A.L.U.).
- lungimea perpendicularei la LDO dusa de la o aeronava ce se afla pe LDR se numeste Abatere Laterala Liniara (A.L.L.).
- punctul in care traiectul isi schimba directia poarta denumirea de Punct de Schimbare de Traiect (P.S.T.), iar segmentele traiectului se numesc Tronsoane.
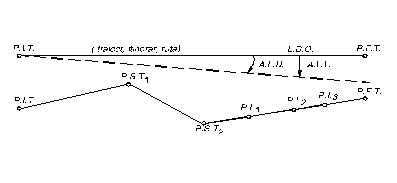
Fig. 2.2. Puncte si linii de navigatie
2.1. Coordonate geografice si coordonate aeriene
Coordonatele geografice reprezinta o metoda de determinare a pozitiei aeronavei fata de suprafata terestra sau a unui reper de pe sol, necesar navigatiei aeriene.
Originea masuratorilor este planul meridianului
Coordonatele geografice se exprima in grade, minute si secunde sexagesimale de Latitudine si Longitudine.
Longitudinea unui
punct oarecare pe suprafata terestra este unghiul format intre planul meridianului prim (
Latitudinea unui punct oarecare pe suprafata terestra este unghiul format intre planul ecuatorului si verticala punctului considerat, adica directia acestuia spre centrul pamantului.
Coordonatele geografice ale unui punct oarecare sunt:
47o20'00' N
27o37'00' E


![]()
![]()
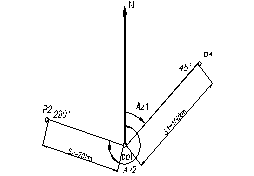
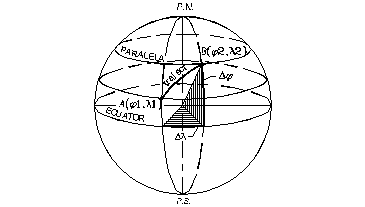
Fig. 2.3. Coordonate geografice Fig. 2.4. Coordonate
polare
Coordonate aeriene sunt:
coordonate polare ;
coordonate rectangulare;
a. Coordonatele polare determina pozitia aeronavei sau a unui reper pe suprafata terestra prin azimut si distanta fata de un punct de referinta numit arbitrar pol. (vezi fig. 2.4.)
Prin azimut (Az) se intetege unghiul dintre directia nord si directia catre un punct considerat. Coordonatele polare se utilizeaza in tehnica operationala radar si in sistemele de navigatie: VOR/DMR, VOR/TAC si TACA Azimutul, care in navigatia aeriana poate fi un relevment, se exprima in grade sexagesimale, iar distanta de la punctul de referinta la pol, in km sau mile marine. Relevmentul se defineste ca fiind unghiul (masurat in sens orar si in grade sexagesimale) format intre directia Nord magnetic si directia ortodromica aeronava/statie sau statie/aeronava.
b. Coordonatele rectangulare determina pozitia unei aeronave pe suprafata terestra exprimata in distante liniare, (masurate in km sau mile marine), pe 2 axe de coordonate perpendiculare intre ele, X si Y. Punctul de intersectie al celor doua axe reprezinta originea masuratorilor si de regula se amplaseaza in punctul initial al traiectului. Calculatorul de navigatie al avioanelor IL-62 si TU-154 foloseste sistemul de coordonate rectangulare (vezi fig. 2.5.).
2.2. Baza masurarii timpului
La baza masurarii timpului stau cele doua miscari ale pamantului (rotatie si revolutie).
Rotirea pamantului in jurul soarelui se efectueaza in 365,242 zile cu o viteza de aproximativ 30 km/sec. si se numeste miscare de revolutie anuala.
Axa pamantului este inclinata fata de planul elipticei cu un unghi de 66o33', iar miscarea pamantului in jurul axei sale se realizeaza in 23 ore 56 mi 04 sec.,si se efectueaza de la V la E cu o viteza de 1669 km/ora la ecuator si se numeste miscare de rotatie.
Unitatea de timp ce corespunde unei rotatii de 360o in jurul axei terestre se numeste zi. In navigatie se foloseste ziua solara medie care are o durata de 24 ore 04 sec. Inceputul zilei solare medii are loc la 12 noaptea (ora 00.00). Timpul se noteaza de obicei cu T.
Ora calculata
pentru primul meridian poarta denumirea de ora
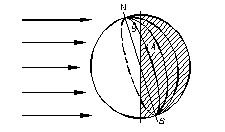
Datorita faptului ca razele soarelui sunt paralele cu planul elipticei, suprafata pamantului luminata de soare este inclinata in raport cu axa polilor cu 23o30'. Din aceasta cauza localitatile amplasate in lungul aceluiasi meridian nu sunt luminate deodata la aceeasi ora (vezi Fig.2.6).
In emisfera de nord, in timpul verii, localitatile situate pe acelasi meridian la latitudini mai mari vor beneficia de lumina soarelui mai mult timp decat cele situate la latitudini mai mici (vezi fig. 2.6.).
Ora rasaritului pentru localitatile de pe un meridian situate la latitudini mai la nord va fi mai devreme fata de localitatile situate mai la sud. La fel si ora apusului soarelui pentru localitatile situate mai la nord va fi mai tarzie fata de localitatile situate mai la sud, pe acelasi meridia


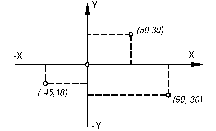
![]()
![]()
Fig. 2.5. Coordonate rectangulare Fig. 2.6. Rasaritul soarelui
2.3. Exprimarea longitudinii in unitati de timp
La o rotire de 24 ore corespund 360o longitudine.
La o rotire de o ora corespund 15o longitudine (360o:24 ore)
Un minut de timp va avea 15' longitudine (15x60)/60.
Deci: 1 ora = 15o longitudine .
1 mi= 15'longitudine.
1 sec.= 15'longitudine.
In mod similar vom obtine:
1olongitudine = (1 ora x 60 )/ 15 = 4 min de timp
1'longitudine = (4 min x 60 )/ 60 = 4 sec de timp
1'longitudine = 4 sec / 60 = 1 / 15 sec de timp
2.4. Fusele orare
Fusele orare reprezinta o impartire a pamantului in fisii (in numar de 24 corespondente celor 24 ore ale zilei).
Fusele orare sunt numerotate de la 0 la 12, iar 'Fusul 0' se intinde de la 7o30'E la 7o30'W.
Fiecare fus orar se intinde pe un arc de 15o longitudine. (1o long. masurat pe ecuator = 1 NM = 1852 m.)
3. LINII DE POZITIE A AERONAVEI
Determinarea pozitiei aeronavei in raport cu suprafata pamantului se realizeaza cu ajutorul unui sistem de coordonate geografice, polare sau rectangulare. In practica navigatiei aeriene este necesar sa se determine elementele deplasarii aeronavei pe baza succesiunii coordonatelor aeronavei. In mod obisnuit aceasta se realizeaza prin determinarea a 2 linii (puncte de pozitie succesive).
Linia de pozitie este locul geometric al tuturor punctelor care pot reprezenta pozitia aeronavei pe suprafata pamantului.
3.1. Loxodroma este linia de pozitie care intersecteaza meridianele sub acelasi unghi (vezi Fig.3.7.).
Loxodroma este linia care trece prin punctul de plecare PIT si punctul de sosire PFT al drumului aerian si taie toate meridianele sub un unghi constant.
Din punct de vedere geometric, loxodroma, prelungita dincolo de capetele drumului apare ca o spirala care se apropie tot mai mult de poli dar fara sa-i atinga. De la aceasta regula fac exceptie paralelele, meridianele si ecuatorul.
Navigatia aeriana care foloseste compasul de la bord se efectueaza pe loxodroma. Navigatia este usoara si convenabila pe distante scurte (sub 1000 Km), deoarece pana la aceasta distanta erorile in lungime sunt mici.
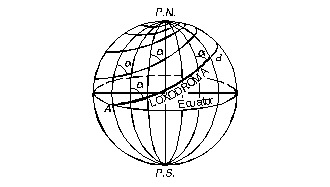
Fig. 3.7. Loxodroma
3.2. Ortodroma este arcul mic din cercul mare care trece prin punctul de plecare PIT si cel de sosire PFT al unui traiect de pe suprafata pamantului (vezi Fig.3.8.).
Ortodroma reprezinta cel mai scurt drum aerian in spatiu intre 2 puncte. Ortodroma se foloseste de obicei la zboruri pe distante mari (peste 1000 km), in cadrul navigatiei radioelectrice (unde pe sol sunt amplasate mijloace radioelectrice dispuse pe ortodroma). Astfel in cadrul unui zbor intre Roma si New York, daca se merge pe loxodroma, vom trece prin: Ankara, Krasnovodsk, Pekin si masoara peste 12.300 km, in timp ce zburand pe ortodroma vom trece prin: Leipzig, Leningrad, Long Eniseisk, Blagowescensk si masoara aproximativ 10.500 km.
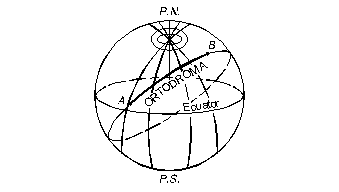
Fig. 3.8. Ortodroma
4. PROIECTII CARTOGRAFICE
Proiectiile cartografice reprezinta niste procedee matematice de transpunere a suprafetei terestre, fie pe o suprafata plana, fie pe o suprafata desfasurabila (care poate fi suprafata unui cilindru sau a unui con), in vederea obtinerii hartilor.
Caracteristicile unei proiectii cartografice sunt:
- sa indice corect unghiurile (sa fie conforme);
- sa pastreze proportionalitatea distantelor (sa fie echidistante);
- sa prezinte forma adevarata a terenului (sa fie echivalente).
- ortodroma si loxodroma, principalele linii de pozitie sa apara ca linii drepte.
- meridianele si paralelele sa fie linii drepte.
Deoarece nici o proiectie cartografica nu poate indeplini aceste conditii simultan, se cauta sa se respecte conditia principala pentru navigatia aeriana si anume sa se respecte unghiurile.
4.1. Elementele unei proiectii
Elementele unei proiectii sunt:
- centrul de vedere, adica punctul din care se executa proiectia;
- razele de proiectie, adica razele imaginare care pleaca din centrul de vedere, strabat suprafata de proiectat (a pamantului) si se proiecteaza pe suprafata de proiectie;
- suprafata de proiectie, adica planul pe care razele de proiectie proiecteaza (dau imaginea) suprafata pamantului.
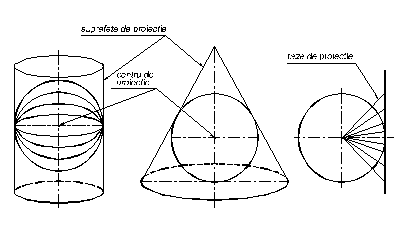
Fig. 4.9. Elementele proiectiilor cartografice
Proiectiile cartografice se clasifica dupa 3 criterii :
a. dupa felul deformarilor;
b. dupa suprafata de proiectie;
c. dupa pozitia punctului de vedere;
a. dupa felul deformarilor:
- proiectii conforme, care pastreaza egalitatea unghiurilor de pe suprafata pamantului;
- proiectii echidistante, care pastreaza o corecta proportionalitate a distantelor;
- proiectii echivalente, care pastreaza proportionalitatea si forma suprafetelor.
b. dupa suprafata de proiectie:
- dupa forma suprafetei:
cilindrica;
conica si policonica;
azimutala.
- dupa dispunerea fata de suprafata pamantului:
tangente;
secante.
- dupa pozitie:
normale (in prelungirea axei pamantului);
transversale (perpendiculare pe axa pamantului);
oblice (in alta pozitie fata de pamant). (Vezi Fig. 4.9.).
c. dupa amplasarea punctului de vedere:
- centrale, cand punctul de vedere este amplasat in centrul pamantului;
- stereografice, cand punctul de vedere este amplasat undeva in spatiu;
- ortografice, cand punctul de vedere este amplasat la infinit.
4.3 Proiectia conica normala
Proiectia conica normala se obtine prin proiectarea elipsoidului terestru pe un con tangent avand inaltimea in prelungirea axei terestre.
Fata de proiectia tangenta, proiectia conica secanta (proiectia conica conforma Lambert), are o zona mai mare in care deformarile sunt mici. Aceasta proiectie este larg utilizata la intocmirea hartilor de navigatie (ex: harta de navigatie a lumii).
Aceste harti pastreaza o singura scara cand paralele standard (paralelele secante) sunt distantate pana la 10o -15o latitudine.
Proiectia conica conforma Lambert are urmatoarele caracteristici:
- este conforma;
- este echidistanta;
- este echivalenta;
- meridianele apar ca linii drepte convergente, iar paralelele, arcuri de cerc concentrice;
- ortodroma si loxodroma nu sunt linii drepte.
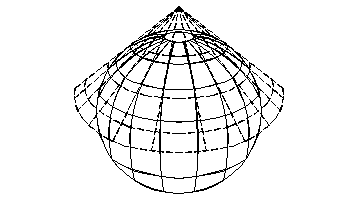
Fig. 4.10. Proiectia conica normala
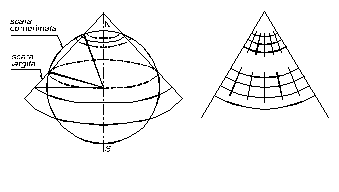
Fig. 4.11. Proiectia conica conforma Lambert
Este o proiectie centrala avand ca suprafata de proiectie un cilindru circumscris de-a lungul ecuatorului. Prin desfasurarea cilindrului se obtine proiectia cilindrica centrala normala.
Proiectia are urmatoarele caracteristici:
- meridianele sunt linii drepte paralele si echidistante;
- paralelele sunt de asemenea linii paralele insa distanta dintre ele creste cu cat ne apropiem de poli;
- peste 72o latitudine, proiectia nu se mai poate utiliza.
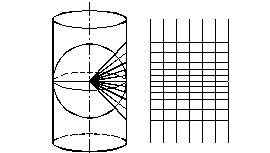
4.5. Proiectia Mercator
Este o proiectie cilindrica normala centrala, modificata in sensul ca deformarea distantelor de-a lungul meridianelor sa fie facuta in aceeasi masura in care acestea sunt deformate de-a lungul paralelelor. In felul acesta scara creste in lungul meridianelor de la ecuator spre poli.
Caracteristicile proiectiei Mercator sunt:
- meridianele sunt linii drepte paralele si egal distantate intre ele;
- paralelele sunt linii drepte paralele dar neegal distantate;
- este conforma;
- nu este echidistanta (scara creste spre poli);
- nu este echivalenta (2 suprafete egale pe teren vor arata diferit pe harta; astfel, cea de la latitudinea de 60o va fi de 2 ori mai mare fata de cea de la ecuator);
- loxodroma este o linie dreapta;
- ortodroma nu este o linie dreapta.


![]()
![]()
Fig. 4.12. Proiectia
cilindrica Fig. 4.13. Proiectia Mercator

![]()
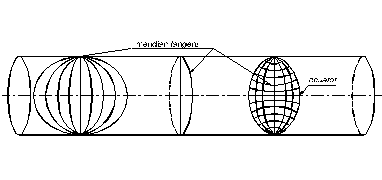
Fig. 4.14. Proiectia cilindrica transversala Gauss
4.6. Proiectia cilindrica transversala GAUSS
In cazul acestei proiectii, cilindrul are axa perpendiculara pe axa pamantului, suprafata fiind tangenta la poli de-a lungul unui meridia
Proiectia are urmatoarele caracteristici:
- meridianul axial se proiecteaza sub forma unei linii drepte perpendiculare pe ecuator fara nici o deformare in ce priveste lungimea sa;
- restul meridianelor se proiecteaza sub forma unor linii curbe, convergente la poli;
- ecuatorul apare ca o linie dreapta;
- paralelele sunt arcuri de cerc dispuse simetric in raport cu ecuatorul;
- proiectia este conforma echidistanta si echivalenta;
- ortodroma si loxodroma nu sunt linii drepte.
4.7 Proiectia stereografica polara
Datorita faptului ca proiectiile cilindrice si conice se folosesc pana la aprox. 60o -70o latitudine, pentru reprezentarea pamantului la latitudini mai mari pe hartile de navigatie se foloseste proiectia stereografica polara.
In cadrul acestei proiectii centrul de vedere se afla la unul din poli iar suprafata tangenta la celalalt pol.
Proiectia are urmatorele caracteristici:
- meridianele apar ca linii drepte convergente la poli;
- paralelele apar ca cercuri concentrice cu centrul la pol, insa distanta dintre ele se mareste pe masura ce ne departam de pol;
- ortodroma se apropie foarte mult de o linie dreapta;
- loxodroma este o linie curba;
- proiectia nu este echivalenta.
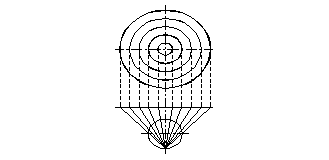
Fig. 4.15. Proiectia polara
5. HARTA
Harta este o reprezentare (transpunere) conventionala pe un plan de dimensiuni reduse a suprafetei elipsoidului terestru, sau a unei parti a acesteia folosind un sistem de proiectie cartografica.
La o harta trebuiesc luate in considerare urmatoarele caracteristici:
a. scara hartii;
b. proiectia cartografica;
c. nivelmentul;
d. planimetria;
e. hidrografia;
f. semne conventionale si alte date generale.
a. scara hartii reprezinta raprtul dintre distanta 's' masurata pe harta si distanta reala 'S' masurata pe teren, folosind aceeasi unitate de masura. Ea se exprima printr-un raport s/S = 1/n sau 1:n; unde n arata de cate ori distanta s de pe harta se cuprinde in distanta reala S de pe tere
Scara hartii poate fi:
- scara numerica, 1:500.000 sau 1/ 500.000;
Numaratorul se exprima prin cifra 1, iar numitorul arata de cate ori este mai mica harta fata de suprafata de teren pe care o reprezinta;
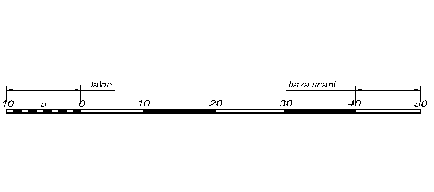
- scara grafica. Acest mod de exprimare al scarii hartii este o reprezentare grafica a scarii numerice.
- scara naturala este scara in care se arata direct valoarea de transformare a masuratorilor de pe harta (ex: 10 cm = 5 Km. sau 10 cm = 10 Km.).
De regula hartile au o scara grafica si o scara numerica.
b. proiectia cartografica este elementul care permite cunoasterea caracteristicilor principale ale hartii respective.
c. nivelmentul reprezinta totalitatea formelor de relief. Reprezentarea nivelmentului pe harta se realizeaza prin curbe de nivel, tente hipsometrice, tente umbrite si cote.
d. planimetria reprezinta totalitatea
constructiilor de pe teren: poduri, terenuri, orase, cai ferate,
drumuri etc.
e. hidrografia infatiseaza cursurile de apa de pe terenul reprezentat;
f. formele conventionale sunt simboluri folosite pentru ca harta sa reprezinte cat mai sugestiv elementele de pe teren: localitati, cai ferate, poduri, etc..
Fig. 5.16. Scara hartii
5.1. Hartile aeronautice
Hartile aeronautice sunt destinate:
- calculelor preliminare a traiectelor de navigatie;
- orientarii la vedere si navigatiei estimate;
- navigatiei radioelectrice;
- procedurilor de operare IFR si VFR (zbor instrumental si zbor la vedere).
Se deosebesc:
- harta traiectelor de navigatie: scara 1:500.000, 1:1.500.000;
- harta de navigatie pentru avioane de mare viteza scara 1:3.000.000;
- harta lumii scara 1:1.000.000. Aceasta este harta de baza pentru navigatia la vedere pe distante medii;
- harta de navigatie la vedere scara 1:500.000 care deriva din harta lumii dar are mai multe elemente;
- harta de radionavigatie scara 1:500.000 - 1:2.000.000, contine axele cailor aeriene, directiile magnetice, nivelele minime de zbor, puncte obligatorii de raport, frecventele si indicativele mijloacelor de radionavigatie si a organelor de trafic si alte informatii;
- harta procedurii de apropiere dupa instrumente, scara 1:250.000 contine elemente topografice si hidrografice precum si elementele de navigatie radioelectrica pentru executarea procedurilor;
- harta procedurii de apropiere la vedere, scara 1:200.000 contine aceleasi elemente, dar in conditii de zbor VFR (zbor la vedere);
- harta regiunii terminale de control la scara 1:50.000 destinata procedurii de trecere de la navigatia pe cai aeriene la apropierea pentru aterizare. Ea contine rute de plecare si sosire pe directiile de decolare - aterizare;
Fig. 5.17. HARTA AERONAUTICA Scara 1:500.000
- harta de aterizare la scara 1:25.000 contine dimensiunile pistelor si elemente de amplasare generala a mijloacelor si cladirilor aeroportului (aeroclubului);
- harta de aerodrom, scara 1: 10.000 contine informatii detaliate privitoare la pista, caile de circulatie si platforma.
6. MAGNETISMUL TERESTRU
Magnetismul terestru reprezinta un ansamblu de fenomene magnetice datorate constitutiei neomogene a planetei noastre (nucleul pamantului este constituit din fier si nichel care datorita temperaturilor si presiunilor mari precum si datorita rotatiei, genereaza fenomenul de inductie magnetica). Magnetismul terestru suporta si influente extraterestre.
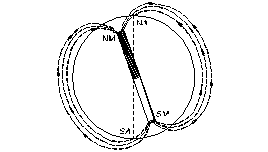
Pamantul se considera ca actioneaza ca un magnet de dimensiuni enorme (vezi Fig. 6.18.) avand caracteristicile si proprietatile unei bare magnetice.
Campul magnetic, forma de manifestare a magnetismului terestru, se caracterizeaza prin liniile de forta magnetica (vezi Fig.6.18.)
Punerea in evidenta a campului magnetic terestru se realizeaza cu ajutorul unui ac magnetic suspendat, liber a se roti in plan orizontal. Acul se va orienta intotdeauna de-a lungul liniilor de forta magnetica care actioneaza asupra lui. Directia de orientare a acului magnetic se considera a fi directia meridianului magnetic. (vezi Fig.6.18.).
Polul nord magnetic si polul nord geografic nu coincid.
Diferenta unghiulara intre directia nordului geografic si directia nordului magnetic (dintre meridianul adevarat si magnetic al locului) se numeste declinatie magnetica si se noteaza cu Dm
Daca se unesc toate punctele de pe suprafata pamantului cu aceeasi declinatie magnetica, se obtin niste curbe, numite izogone.
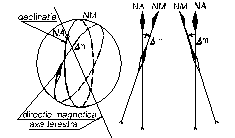
Declinatia magnetica poate fi estica (pozitiva) sau vestica (negativa) (vezi Fig.6.19.), in functie de amplasarea meridianului magnetic fata de cel geografic.
Datorita faptului ca nordul magnetic nu coincide, ci se deplaseaza in jurul polului nord geografic, executand o rotatie de 360o in timp de peste 800 de ani, declinatia magnetica este variabila.
Din aceste motive pe harti sunt trecute in dreptul liniilor izogone data cand au fost trasate, cat si variatia anuala a acestora.
In tara noastra variatia declinatiei magnetice este de 5,1' E pe a Pentru a afla declinatia magnetica din prezent, se va inmulti diferenta de ani (de la data editarii hartii si pana la data calculului) cu variatia declinatiei (5,1' x nr. de ani) si se va aduna la declinatia trasata pe harta.
Pe harti se traseaza si liniile care au aceeasi inclinatie magnetica si care se numesc izocline.
Unghiul de inclinatie magnetica este 0o la ecuator si 90o la poli.
Liniile care au declinatia 0o se numesc linii agone.
Datorita faptului ca structura geologica a pamantului este foarte diferita din punct de vedere magnetic, de la loc la loc, vom intalni pe hartile de navigatie aeriana, in afara liniilor de egala declinatie si linii (zone) unde valoarea campului magnetic este foarte puternica si cu izogonele deformate. Aceste zone de anomalii magnetice se pot intinde de la cateva zeci de metri la cateva sute de Km. O astfel de zona, unde intensitatea campului magnetic este aproape similara cu regiunea polilor, este regiunea Kursk din Rusia (zona cu bogate zacaminte de fier).
In afara acestor anomalii, campul magnetic terestru este supus si unor perturbatii cu un caracter aleator. Aceste perturbatii se numesc furtuni magnetice si au loc in general in zona polilor, dar se mai produc si pe intreg globul.
Cauzele acestor furtuni magnetice sunt legate de aparitia petelor solare, care au o periodicitate de 11 ani. Petele solare sunt zone de emisie a particulelor ionizate care au propriul lor camp magnetic si care interfera cu cel terestru.
Durata acestor furtuni este de cateva ore; in schimb sunt foarte puternice, inregistrandu-se furtuni in cadrul carora declinatia s-a modificat cu 52o. In timpul acestor furtuni acul magnetic este foarte instabil.


![]()
![]()
Fig. 6.18. Magnetismul terestru Fig. 6.19. Declinatia magnetica
7. ELEMENTE DE NAVIGATIE AERIANA
Acestea sunt :
- actiunea vantului asupra planorului (deriva);
- actiunea vantului asupra vitezei fata de sol;
- drumuri, capuri;
- trasarea drumurilor.
In acest capitol sunt definite elementele care se calculeaza la sol inaintea inceperii zborului, elemente necesare echipajului pentru efectuarea zborului.
Directia indica pozitia sau orientarea unui punct in spatiu, in raport cu un alt punct, fara a tine seama de distanta dintre ele.
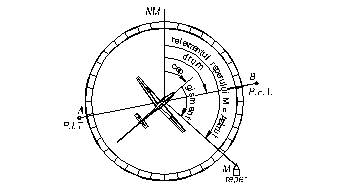
Fig. 7.20. Directii
Determinarea directiei se poate face in plan orizontal sau in plan vertical.
In navigatia aeriana se folosesc ca directii drumurile, capurile si relevmentele.
7.1. Drumurile aeronavei
Drumul este unghiul format intre directia nordului (Nord Adevarat, Nord Magnetic) si linia care uneste Punctul Initial al Traiectului cu Punctul Final al Traiectului.
Se deosebesc deci, drumuri adevarate (DA) si drumuri magnetice (DM) (vezi Fig. 7.21.).
Cand traiectul aeronavei coincide cu linia drumului obligat (LDO), atunci drumurile masurate se numesc drumuri (adevarate sau magnetice) obligate (DAobl, DMobl).
Cand traiectul real al aeronavei nu coincide cu LDO, drumurile se numesc drumuri (adevarate sau magnetice) real urmate (DAr, DMr).
Masurarea drumurilor pe harta se realizeaza astfel:
- se uneste PIT cu PFT pe harta;
cu ajutorul unui raportor se masoara unghiul format intre directia celui mai apropiat meridian geografic si LDO.
Abaterea laterala unghiulara este unghiul format intre linia drumului obligat LDO si linia drumului real LDR. Se noteaza ALU.
Lungimea perpendicularei dusa din punctul unde se afla aeronava pe LDR la LDO se numeste abatere laterala liniara (ALL).
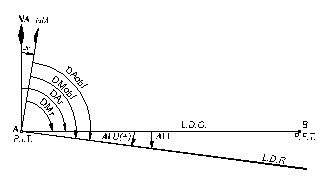
Fig. 7.21. Drumuri in navigatia aeriana
7.2. Capurile aeronavei
Unghiul format intre directia nordului si axa longitudinala a aeronavei se numeste cap (vezi Fig. 7.22.).
Daca directia de referinta este cea a nordului adevarat, se numeste cap adevarat (CA), iar daca este a nordului magnetic, capul va fi cap magnetic (CM).
Instrumentul cu care se citeste capul magnetic este Compasul de aviatie (busola) (vezi Cap. Instrumente de bord).
Acesta, in afara liniilor magnetice de forta, mai este supus si campului magnetic al maselor metalice din structura aeronavei precum si a campului electromagnetic generat de circuitele si agregatele electrice de la bord. Din acest motiv compasul de aviatie nu va indica directia meridianului magnetic, ci o alta, numita directia nordului compas (NC).
Unghiul format intre directia nordului magnetic (NM) si cea a nordului compas (NC) se numeste deviatia compasului si se ia in considerare la calculul elementelor de navigatie.
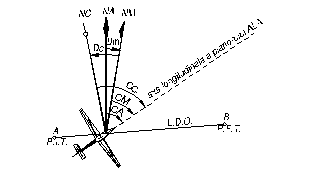
Fig. 7.22. Capurile aeronavei
7.3. Relevmentul
Relevmentul avionului este unghiul masurat intre meridianul care trece prin punctul de amplasare al mijlocului de radionavigatie si directia ortodromica catre punctul avionului.
Relevmentul statiei este unghiul masurat intre meridianul care trece prin punctul de amplasare al avionului si directia ortodromica catre mijlocul de radionavigatie.
In cadrul aviatiei sportive nu se foloseste de obicei relevmentul, totusi este bine sa fie cunoscut pentru cazurile de pierdere a orientarii, cand se apeleaza la turnurile de control ale aviatiei de transport.
In aceste situatii turnul de control va transmite aeronavei prin radio relevmentul magnetic al reperului (RMR = QDM) sau relevmentul magnetic al avionului (RMA = QDE).
QDM reprezinta directia magnetica pe care ne deplasam pentru a ajunge la turnul de control (reper), iar QDE reprezinta directia magnetica pe care se afla aeronava fata de reper.
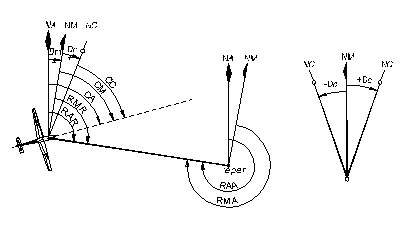
Fig. 7.23. Capurile si relevmentele
Drumuri-Capuri: relatii de calcul
Drumurile folosite in navigatia aeriana sunt in general trasate pe harta incepand cu linia drumului adevarat LDO. Prin masurare pe harta se va determina DA si prin calcul se va afla drumul magnetic DM, apoi cunoscand deviatia compasului se va calcula drumul compas DC cu urmatoarele relatii:
DA = DM + ( Dm)
DM = DA - ( Dm)
DC = DM - ( Dm)
DM = DC + ( Dm)
DA = DC + ( Dc) +( Dm)
DC = DA - ( Dc) +( Dm)
Exemplu
DA = 70o; Dm = 5o;
DM = 70o - 5o = 65o
In timpul zborului la bordul aeronavei se citeste direct la compasul de aviatie, capul compas. Acesta se masoara intre directia nord compas (directia nord indicata de compas), si prelungirea axei longitudinale a aeronavei, partea din fata. (vezi Fig. 7.22.).
Relatiile de calcul sunt:
CM = CA - ( Dm)
CA = CM + ( Dm)
CC = CM + ( Dc)
CM = CC - ( Dc)
CC = CA - ( Dm) - ( Dc)
CA = CC + ( Dm) + ( Dc)
Exemplu
CM = 60o; Dm = 5o;Dc = +2o
CM = 60o- 5o= 55o
CC = 55o- 2o= 53o
7.4. Unghiul de deriva
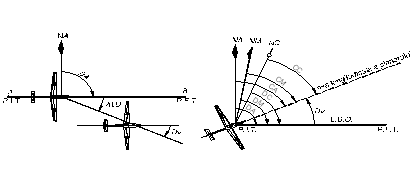
Ultimul element care determina modul de desfasurare a zborului este deriva sau unghiul de deriva, care se datoreaza directiei si vitezei de deplasare a masei de aer in care zboara aeronava. Prin deriva se intelege unghiul format intre prelungirea axei longitudinale a aeronavei si linia drumului real si se noteaza Dv.
Deriva aeronavei variaza in functie de viteza vantului, directia acestuia fata de LDO (Unghiul Drumului cu Vantul), cat si de viteza proprie a aeronavei (V.P.A.)
Variatia derivei se manifesta astfel:
- cu cat viteza vantului este mai mare, cu atat unghiul derivei va fi mai mare;

![]()
Fig. 7.24. Deriva aeronavei
- cu cat unghiul directiei vantului fata de LDO (UDV) este mai mare, cu atat unghiul de deriva va fi mai mare. (UDV poate avea valori cuprinse intre 0o si 180o stanga/dreapta fata de LDO).
- cu cat viteza proprie a avionului este mai mare, cu atat unghiul de deriva este mai mic.
7.5. Relatiile de calcul intre drumuri si capuri
Relatiile de calcul intre drumuri si capuri sunt urmatoarele:
CA = DA - ( Dv)
CM = DM - ( Dv) = DA - ( Dm) - ( Dv)
CC = DM - ( Dc) - ( Dv) = DA - ( Dm) - ( Dc) - ( Dv)
DA = CC + ( Dc) + ( Dm) + ( Dv)
Calcularea derivei si a celorlalte elemente necesare desfasurarii zborului se realizeaza cu ajutorul metodelor grafice (triunghiul de navigatie al vitezelor) sau cu ajutorul calculatoarelor de navigatie.
7.6. Actiunea vantului asupra vitezei la sol
Dupa cum se stie, vitezometrul indica viteza de zbor a aeronavei fata de masele de aer (VPA).
In acelasi timp masele de aer se vor deplasa fata de sol. Din acest motiv si viteza aeronavei fata de sol (VS) va fi diferita de viteza proprie a aeronavei. Aceasta viteza depinde de viteza vantului, dupa cum urmeaza:
- viteza aeronavei fata de sol creste atunci cand vantul este de spate;
- viteza aeronavei fata de sol scade cand vantul este de fata;
7.7. Triunghiul de navigatie al vitezelor
Triunghiul de navigatie al vitezelor reprezinta procedeul de baza pentru determinarea elementelor principale de navigatie ale zborului.
Triunghiul de navigatie al vitezelor se compune din 3 vectori:
- vectorul vitezei proprii;
- vectorul vitezei vantului;
- vectorul vitezei fata de sol.
Cunoscand 2 vectori se determina cel de-al treilea si deriva.
Triunghiul de navigatie al vitezelor se poate rezolva grafic, analitic si cu ajutorul calculatoarelor de navigatie sau a oricarei rigle de calcul.
Rezolvarea grafica a triunghiului de navigatie al vitezelor este prezentata in continuare: (vezi Fig. 7.25.)
De obicei se cunosc drumul adevarat DA, viteza proprie adevarata VPA, directia si viteza vantului. Se cere sa se determine deriva (Dv), viteza fata de sol (VS) si capul adevarat (CA).
Se traseaza pe o coala de hartie o scara grafica convenabila care sa cuprinda atat viteza vantului Vv cat si viteza proprie adevarata VPA. Dintr-un punct ales ca origine, 'O', se traseaza linia drumului obligat LDO. In originea aleasa se amplaseaza si vectorul vant la aceeasi scara si anume cu originea vectorului in punctul 'O'. Din varful vectorului vant (punctul A), de regula cu ajutorul unui compas, se traseaza un arc de cerc cu o raza egala cu VPA care se intersecteaza cu LDO. In acest punct de intersectie, B, se amplaseaza un nou vector Vv, cu varful pe LDO. Se uneste punctul de origine 'O' cu originea vectorului vant Vv (punctul C).
S-au obtinut 2 triunghiuri asemenea in care:
AB = OC = VPA
OB = Vs (se masoara pe scara grafica) iar unghiul BOC = Dv se masoara cu raportorul.
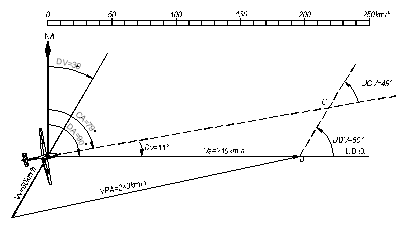
Fig. 7.25. Rezolvarea grafica a trunghiului de navigatie al vitezelor
Unghiul format intre linia drumului obligat si directia vantului se numeste unghiul drumului cu vantului (UDV) (masurat invers, devine UVD). El se masoara pe ambele parti ale LDO de la 0o la 180o.
Unghiul format intre axa longitudinala a avionului (partea din fata) si directia vantului se numeste unghiul capului cu vantul (UCV) (masurata invers, devine UVC).
UVC va fi intotdeauna mai mic decat UVD cu valoarea derivei.
Exemplu:
DA = 90o; Vv = 30o /60 Km/h;
VPA = 240 Km/h
Rezolvand grafic (vezi Fig.7.25.), se obtine:
Dv = 11o; Vs = 220 Km/h;
CA = 79o; UVD = 60o;
UVC = 49o ;
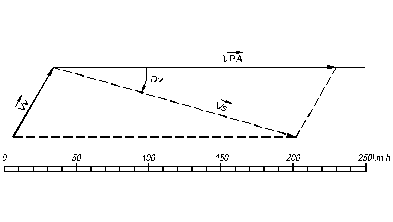
Pentru rezolvarea grafica a triunghiului de navigatie al vitezelor se poate proceda si astfel :
In punctul 'O' de pe LDO se aplica vectorul VPA si Vv (vezi Fig.7.26).
Construind paraleleogramul
fortelor se obtine componenta
Cunoscand drumul adevarat DA, se poate calcula capul adevarat CA cu ajutorul urmatoarei formule :
CA = DA - ( Dv)
Viteza
la sol se obtine masurand pe scara grafica lungimea vectorului
OB.

A
O
B
![]()
Fig. 7.26. Rezolvarea grafica a triunghiului de navigatie al vitezelor
Pentru
rezolvarea analitica a triunghiului de navigatie al vitezelor se
foloseste Teorema sinusurilor intr-un triunghi oarecare. (vezi Fig.7.27.)
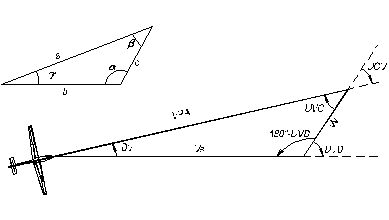
a b c
sin a sin sin t
Fig. 7.27. Rezolvarea analitica a triunghiului de navigatie al vitezelor
In relatia de mai sus, cunoscand trei elemente, se poate determina cel de-al patrulea. Aceasta relatie se poate aplica si la triunghiul de navigatie al vitezelor. Sunt necesare 2 precizari :
- unghiul adiacent al lui UVD este 180o-UVD, iar sin (180 o -UVD)= sin UVD;
- unghiul opus vectorului VS este UVC. Relatia va deveni:
----- ----- --------- = ------------- = ----------
sin(180o-UVD) sin UVC sin Dv
Pentru exemplul din Fig.7.25, se obtin urmatoarele valori:
UVD = 90o - 30o = 60o
240Km/h 60 Km/h 240 60
----- ----- ---------- = ----- ----- ----- sau ------------ = ---------- de unde:
sin (180o-60o) sin Dv sin 60o sin Dv
sin Dv = 0,22, rezulta Dv = 12o40'.
Vs = 205,5 Km/h;
CA = DA - (Dv) = 90o - 12 o = 78o.
Cunoscand capul adevarat, prin rezolvarea triunghiului de navigatie al vitezelor se poate afla capul compas.
Cunoscand declinatia magnetica (citita pe harta) si deviatia compasului (citita la bordul aeronavei), capul compas se calculeaza dupa formula:
CC = CA - ( Dm) - ( Dc) - ( Dv)
8. PROBLEME DE ALTIMETRIE
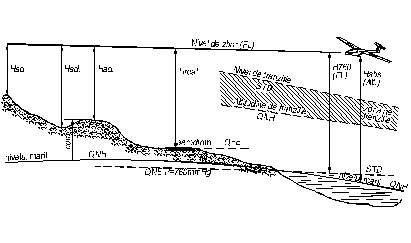
Aceste probleme se intalnesc in navigatia aeriana datorita deselor situatii cand va trebui sa urcam cu aeronava pana la o anumita inaltime. In cadrul acestor zboruri vom intalni urmatoarele defintii pentru inaltimi:
Inaltimea absoluta (H Abs) sau Altitudinea este distanta pe verticala masurata de la nivelul mediu al marii pana la punctul considerat unde se afla aeronava.
Inaltimea relativa (H Rel) sau inaltimea, este distanta pe verticala masurata de la suprafata de referinta a aerodromului pana la punctul considerat pentru masurarea inaltimii.
Inaltimea nivelului 91 (2700m) sau nivelul de zbor (FL), este distanta pe verticala masurata fata de suprafata izobarica de 760 mm col.Hg sau 1013.25 mb (HPa).
Inaltimea reala sau adevarata (H real sau H adev) este distanta pe verticala masurata dintre obstacolul survolat si aeronava. Datorita neregularitatilor terenului aceasta inaltime este variabila pe tot parcursul zborului.
Cota este inaltimea obstacolului masurata fata de nivelul mediu al marii.
In functie de aceste inaltimi in timpul zborului, organele de trafic vor transmite la echipaje urmatoarele presiuni:
- QNH = presiunea redusa la nivelul marii;
- QFE = presiunea la nivelul pistei;
- QNE (Std) = presiunea de referinta de 760 mm col Hg sau 1013.25Mb (HPa).
Treapta barica este distanta pe verticala dintre 2 planuri a caror diferenta de presiune este egala cu un mb (Hp).
1 hPa = 8.4 m;
1 mm col Hg = 11.2 m

![]()
Fig. 8.28. Inaltimi in navigatia aeriana
Astfel apar situatii cand in cadrul problemelor se cere sa se execute calcule si transformari din mmHg in mb (hPa) cat si transformari in functie de punctele de referinta fata de care se fac masuratorile.
Exemplu : O aeronava va decola de pe un aerodrom dupa QFE si va trebui sa urce pana la un anumit nivel (FL) dupa Std. Cunoscand cota aerodromului si presiunea se poate calcula ce spatiu pe verticala va avea de parcurs aeronava, deci timpul necesar si respectiv consumul de combustibil (pentru avioane).
Zona de tranzitie reprezinta suprafata din spatiul aerian pe verticala in cadrul careia o aeronava in urcare sau coborare executa proceduri de calaj altimetric, trecand pe Std la urcare pentru intrare pe nivelul de zbor FL, sau trecand altimetrul pe QFE-ul aerodromului in situatia executarii procedurilor de aterizare.
8.1. Calajul altimetric
In situatia zborurilor de deplasare de pe un aerodrom pe altul suntem nevoiti de multe ori sa aterizam pe cel de-al doilea si altimetrul va arata o anumita cifra (diferenta de inaltime dintre cele 2 aerodroame).
Pentru a se putea executa in mod corect elementele de apropiere pentru aterizare (la inaltimile impuse de instructiunile de exploatare ale celui de-al doilea aerodrom), trebuie sa executam calajul altimetrului.
Aceasta operatie are rolul de a aduce altimetrul in situatia ca la aterizarea pe noul aerodrom sa arate '0' m inaltime.
Inainte de a decola de pe primul aerodrom, cerem de la organele de trafic sau de la meteo, presiunea din momentul respectiv la pragul pistei de decolare (QFE aerodrom decolare).
Pentru calaj in interiorul altimetrului este introdusa o scala barometrica. Aceasta este vizibila printr-o fereastra a altimetrului si este gradata in mm Hg sau mb.
Operatiunea de calaj (dupa QFE) se realizeaza astfel:
- se aduce inainte de decolare acul altimetrului la '0';
- se desface piulita de la butonul cu cremaliera, se trage butonul spre exterior si se roteste pana cand presiunea indicata in fereastra este cea data de statia meteo sau organele de trafic de pe aerodrom. Dupa acesata se impinge butonul si se strange piulita inapoi.
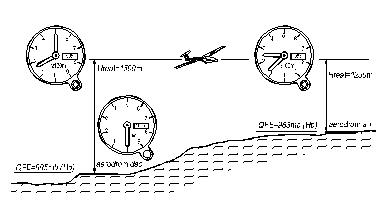
Fig. 8.29. Calajul altimertic
Cu aceasta se poate decola.
In timpul zborului va fi suficient sa cerem presiunea de la pragul pistei de la cel de-al doilea aerodrom (aerodromul de aterizare), sa rotim butonul fara sa mai slabim piulita pana cand in fereastra apare presiunea corespunzatoare celui de-al doilea aerodrom. In timpul rotirii se vor schimba atat indicatiile presiunii din fereastra cat si indicatiile acelor altimetrului (indicatiile de inaltime).
Cand am terminat operatia de rotire a butonului (operatia de calaj), acele altimetrului ne vor arata la ce inaltime ne aflam fata de cel de-al doilea aerodrom.
In momentul cand vom ateriza pe noul aerodrom, altimetrul va indica '0'm inaltime.
Executand calajul altimetrului, avem certitudinea ca vom executa procedurile de apropiere pe noul aerodrom avand inaltimile minime de siguranta la trecerea peste eventualele obstacole de pe langa aerodrom.
9. LUCRUL CU HARTA
In cadrul navigatiei la vedere o importanta deosebita o are cunoasterea in permanenta a pozitiei aeronavei. Pentru aceasta un pilot va trebui sa stie sa compare in permanenta reperele de pe sol cu cele de pe harta, sa aleaga repere caracteristice pe sol, respectiv pe harta, repere care se vor afla la o distanta de cca.15 min de zbor pentru a putea fi in permanenta la vedere. In acest scop pilotul va trebui sa se obisnuiasca sa aprecieze in zbor distantele atat pe harta cat si pe teren, lucru care se realizeaza in urma antrenamentului in zona.
Avand distante cunoscute pe sol, in timpul zborului vom urmari cum se vad de la diferite inaltimi de zbor, pentru ca apoi sa le putem compara cu distante necunoscute din tere Totodata, prin antrenament vom invata aprecierea acestor distante pe harta.
Fiecare pilot planorist, in cadrul zborurilor de antrenament, va trasa pe harta unele cercuri din 5 in 5 Km cu centrul in centrul aerodromului. Aceste cercuri ne vor ajuta la obisnuirea ochiului cu distantele de pe sol. Trebuie mentionat ca odata cu cresterea inaltimii, citirea hartii se face mai greu datorita aplatisarii formelor de relief iar unele detalii sau chiar repere dispar datorita micsorarii vizibilitatii oblice.
In situatia cand se trece la zborul de distanta se recomanda urmatoarele:
- orientarea hartii in sensul deplasarii;
- alegerea unor repere usor de identificat. Se poate intampla ca unele repere de pe harta sa fi disparut din teren si sa fi aparut altele noi;
- la inceperea spiralarii in caminul termic, alegerea de repere noi pe traseu, cat permite vizibilitatea, pentru a sti in ce parte sa parasim caminul termic;
- trebuie tinut cont de faptul ca aspectul general al zonei se modifica in functie de anotimp;
- dupa trasarea pe harta a LDO, se calculeaza capul compas si apoi se studiaza reperele de pe stanga si dreapta traseului, cat si zonele favorabile aparitiei conditiei termice.
10. CALCULE MINTALE
De multe ori in timpul zborului, pentru a pierde cat mai putin timp, in afara de abace, suntem nevoiti sa efectuam si unele calcule mintale care ne ajuta la navigatie.
Calculele mintale se refera la:
- aprecierea distantelor pe harta, lucru care se realizeaza prin antrenament, plecand de la unghiuri de 90o-45o si ajungand la unghiuri de 5o.
- determinarea timpului de zbor se face calculand cat parcurge planorul intr-un minut si apoi facand raportul fata de distanta totala, aflam cat timp vom zbura pana la destinatie.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 4376
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved