| CATEGORII DOCUMENTE |
| Agricultura | Asigurari | Comert | Confectii | Contabilitate | Contracte | Economie |
| Transporturi | Turism | Zootehnie |
| Navigatie |
2. Simularea ca metoda
Studiu de caz (1) Evaluarea mediei unei multimi de numere
Studiu de caz (2) Determinarea probabilitatii de mentinere a legaturii intre nodurile unei retele
Studiu de caz (3) Stabilirea configuratiei unei retelei de transport pe sine
3. Breviar teoretic al simularii 4. Generarea numerelor aleatoare 5. Etapele abordari problemelor prin simulare
Studiu de caz (4) Dimensionarea parcului de vehicule
Studiu de caz (5) Determinarea calificarii fortei de munca pentru echipele de remediere a defectiunilor de pe teren
6. Simularea de sistem
7. Asupra necesitatii simularii
Notatii si simboluri utilizate in cuprinsul capitolului*
A , B , F - functia implicita pentru modele generale sau de parametrii spatiu-timp;
C costul unitar al nefunctionarii unui tronson al retelei sau costul unitar al retribuirii echipei de reparatii,
F - functia de repartitie;
K - costuri cumulate;
L - lungime;
N - numarul de probe pe parcursul simularii;
Q - duratele intre aparitia defectiunilor;
S - identificarea saptaminilor;
T - duratele de remediere ale defectiunilor;
U(0,1) , N(0,1) - repartitia uniforma sau repartitia normala - notatia curenta;
V - costul echivalent al metrului de linie;
X - valoarea numarului real aleator;
Z - valoarea numarului real normat;
a,b,c - valori naturale individualizate;
f - functie de densitate de probabilitate;
i, n - numar de ordine;
k constanta de stare calculata ca raport intre costul curent si costul de referinta;
m - medie pentru o variabila;
pij - probabilitatea de functionare fara avarie;
s2 - dispersie de selectie;
t - variabil timp;
x - abscisa axei reale (dar si elementul de definire al multimilor de numere reale);
xn , yn , wn - notatie auxiliara pentru numere aleatoare sau distribuite dupa anumite legi;
z - ordonata axei reale ;
a b - denumirea generica a unor sisteme;
l - numarul mediu de serviri in unitatea de timp;
m - numarul mediu de serviri in unitatea de timp;
s - deviatie;
W - suprafata delimitata de curbe;
![]() - variabila spatiu (loc, locatie);
- variabila spatiu (loc, locatie);
* aceste notatii si simboluri, ca si numerotarea formulelor, figurilor si tabelelor sunt valabile doar in cuprinsul prezentului capitol.
1. Rezolvare analitica - simulare - optimizare experimentala
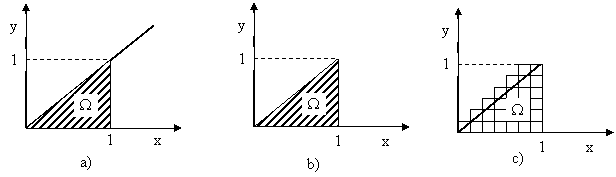 Fie urmatoarea problema (fig. 1) : se cere sa se determine aria W marginita de 3 segmente de dreapta.
Fie urmatoarea problema (fig. 1) : se cere sa se determine aria W marginita de 3 segmente de dreapta.
Problema s-ar putea rezolva prin din 3 (din cele 4 ) tipuri de modele acceptate in cercetarea operationala (mai putin cel procedural):
(a) fizic : decuplarea suprafetei si cantarire;
(b) analogic : decuparea suprafetei si scufundarea ei in lichid cu masurarea volumului dislocuit;
(c) simbolic : integrarea functiei curbei delimitatoare a ariei.
Rezolvarea analitica.
In sistemul de coordonate (x,y) studiul geometriei indica dreapta y=x ca limita intre valorile x0=0 si x1=1 a suprafetei W . Deci:
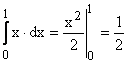 (1)
(1)
Rezolvarea prin simulare.
Se utilizeaza o multime de numere alese la intamplare cu ajutorul carora se constituie puncte in spatiul 1/1 (se admite ca suprafata unui patrat de latura unitara este egala cu 1). De exemplu: (0,3; 0,7), (0,4; 0,3), (0,9; 0,5), (0,3; 0,2), (0,8; 0,8) (0,3; 0,6), etc..
Unele dintre ele vor fi in perimetrul W , altele in exteriorul suprafetei, dar in perimetrul patratului: (0,4; 0,3) in interior, ( 0,3; 0,6) in exterior etc.. Intuitiv se poate presupune ca 'reusitele' vor fi cu atat mai numeroase cu cat suprfata W reprezinta o parte mai insemnata din suprafata patratului. Practic se poate constata ca numarul de reusite este aproximativ egal cu al nereusitelor, cu alte cuvinte o jumatate din aria patratului revine suprafetei W
Rezolvarea prin optimizare experimentala.
Se identifica domeniul de variatie a abscisei x (de la 0 la 1) si se partitioneaza in subdiviziuni ; fie acestea de 0,25. Se procedeaza identic cu variabila y. Cu fiecare valoare din x si fiecare valoare din y se formeaza cate o pereche. Se observa comportarea sistemului in toate patratelele : ori de cate ori perechea cade in interiorul suprafetei W se aduna prin subrutina, initial nula, valoarea 0,25*0,25 = 0,0625 (pentru patratelele care au o pozitie ambigua se adopta o pozitie neutra : jumatate din cazuri se aduna, jumatate nu). Rezulatul, tot 1/2.
Ce deosebeste cele trei cai de rezolvare:
existenta la primele doua a unui model (analitic sau probabilistic) vis-a-vis de inexistenta vreunui model in a treia (o enumerare pur si simplu);
existenta la ultimele doua a procedeelor iterative (se repeta alegerea numerelor intamplatoare sau alegerea patratelelor) vis-a-vis de executia directa prezenta la prima cale;
in concluzie : optimizarea experimentala se deosebeste de simulare prin inexistenta vreunui model predefinit al problemei de rezolvat.
2. Simularea ca metoda
In timp ce modelele reprezinta realitatea, simularea o imita. In termeni tehnici, a simula inseamna a pretinde sa se ajunga la esenta fara realitate (in acest sens orice reprezentare este o forma de simulare deoarece, orice reprezentare implica inevitabil o oarecare reducere sau schimbare a realitatii).
De aceea una din definitiile sintetice ale simularii este : imitarea realitatii intr-o forma echivalenta. Consecinta directa a acestei abordari : simularea nu poate fi o metoda de rezolvare comparabila cu procedeele analitice ale cercetarii operationale de exemplu, pentru ca se poate imita ceva numai daca este cunoscut dinainte, nemijlocit, mijlocit, sau cel putin in stadiul de ipoteza. Concluzia : simularea insasi nu va furniza in principiu cunostiintele noi, ci va oferi numai posibilitati si cai noi pentru a ajunge la un rezultat inca necunoscut. In principiu, orice model poate fi rezolvat prin simulare, dar ea este cu adevarat necesara cand se simuleaza cu intentia de a se evita dificultatile care ar ingreuna sau chiar ar face imposibila solutionarea in alt mod a problemei.
Simularea cauta sa invinga dificultatile mentionate prin teste* repetate ale unor ipotetice solutii. De fapt, intotdeauna cand metodele clasice nu functioneaza, datorita complexitatii situatiei si/sau numarului mare de reactii si/sau variabile, se recurge la acest procedeu iterative. Recurgand la un astfel de procedeu trebuie sa se dispuna de o solutie initiala (care in general nu este optima) si de o serie de reguli (un algoritm ) care permit imbunatatirea ei (solutia noua va fi la randul ei, modificata pana cand nu mai e posibil in directia vizata sau prelungirea calculelor implica cheltuieli nejustificate).
Pe de alta parte, obtinerea unui rezultat se face cu scopul de a-l aplica intr-o forma oarecare realitatii. Pentru acest motiv intre model si realitate trebuie sa existe o relatie bijectiva (care permite deci si retroversiunea de la model la realitate). Astfel construirea unei simulari devine o parte importanta in procesul care duce de la formularea unei problemei la solutia ei. Deoarece procesul mentionat este grevat de numeroase influente exogene, echilibrul unei simulari este asigurat de o disciplinare accentuata endogena (cantitatea totala de incertitudine este pastrata in limite acceptabile printr-o alcatuire interna foarte exacta).
Cum se obtine simularea unui sistem complex ? Nu exista o metoda uniforma recomandata pentru construirea unei simulari! Totusi se pot identifica o serie de trasaturi caracteristice care dirijeaza cercetatorul catre finalizare:
cuvantul de ordine in construirea unei simulari este asigurarea posibilitatii de efectuare usoara a experimentelor. Acest lucru este sinonim cu : o modelare flexibila a fenomenului analizat si o interfata prietenoasa (datele de intrare, iesire si cele intermediare trebuie sa poata fi accesate lesnicios);
desi numarul de factori care afecteaza rezultatele este mare si o comparatie valabila intre diferite variante ar putea fi facuta numai dupa o verificare exhaustiva, exista metode factoriale ale interactiunii care inlatura experimentarea completa;
neavand nevoie de presupuneri simplificataore simularea depaseste cadrul modelarii simple, eludand etapa ierarhizarii si selectarii variabilelor: simularea este un model care functioneaza ; avantaj : algoritmul poate fi oricat de complicat se doreste, el va conduce la solutie ; dezavantaj: simularea este limitata la analiza comportarii sistemului asa cum a fost imaginat, in orice conditii date (simularea este un instrument de analiza care poate fi denumit 'daca . atunci');
simularea are nevoie de un ansamblu de modele descriptive si explicative care se constituie intr-un algoritm de lucru.
Studiu de caz (1) Evaluarea mediei unei multimi de numere
Se doreste sa fie evaluata valoarea medie a patratelor unei variabile care poate lua orice valoare cuprinsa intre 0 si 999 cu aceeasi probabilitate 0,001. Se pot imagina doua cai analitice:
(a)
![]()
(b) ![]()
unde n = 999 este numarul elementului final.
Si prin simulare se pot imagina doua cai:
(a) se considera de exemplu 10 numere intimplator alese intre 0 si 999. Fie acestea xi din tab. 1.
Tab. 1 Prima modalitate de rezolvare prin simulare
|
n |
|
|
|
Daca exista resurse, se poate continua si o constata apropierea de valoarea reala ('necunoscuta' in ipoteza simularii de fata).
(b) se aleg numerele intamplatoare, dar se face acest lucru pragmatic, adica se alege cate unul din fiecare suta pe care se intinde domeniul, tab. 2.
Se poate constata ca rezultatul este mult mai aproape de solutia analitica. Concluzia este ca alegerea numerelor vehiculate intr-o simulare influenteaza puternic solutia obtinuta, sau, altfel spus, un capitol important al tehnicii simularii trebuie sa il reprezinte modalitatea de obtinere a numerelor aleatoare*.
Tab. 2 A doua modalitate de rezolvare prin simulare
|
n |
|
|
|
Studiu de caz (2) Determinarea probabilitatii de mentinere a legaturii intre nodurile unei retele
Pentru fiecare din conexiunile unei retele (pentru fiecare arc al grafului asociat fig. 2 ) se cunosc probabilitatile de a suferi o avarie pij - tab. 3 (de a se intrerupe continuitatea caii de rulare sau furnizarea energiei electrice, de exemplu).
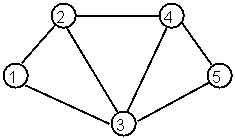
Fig. 2. Graful asociat retelei de alimentare
Tab. 3 Probabilitatea de functionare fara avarie a retelei pij
|
I / J | |||||
Se doreste determinarea probabilitatii de a avea o legatura intre punctul 1 si punctul 5. Rezolvarea analitica este destul de laborioasa (iar daca numarul conexiunilor este mare, dificultatile cresc peste masura). Simularea se constitue pe urmatoarea logica : pentru a estima probabilitatea ca 1 sa comunice cu 5, procedeul cel mai simplu este de a alege la intamplare cate un sistem format din 7 cifre, corespunzator celor 7 legaturi 12,13, 23, 24, 34, 35, 45. Daca prima cifra este 0, 1, 2 se poate presupune ca legatura 12 este in functie, iar in caz contrar, este avariata, etc. (tab. 4).
Tab. 4 Procedura de rezolvare a problemei mentinerii legaturii in retea
|
Legatura |
Succes |
|||||||
|
Prob. | ||||||||
|
X |
||||||||
|
X |
||||||||
|
X |
||||||||
|
|
X |
|||||||
|
X |
||||||||
|
X |
||||||||
|
X |
||||||||
|
X |
||||||||
|
X |
||||||||
|
X |
||||||||
|
X |
||||||||
|
X |
||||||||
|
X |
||||||||
|
X |
||||||||
|
X |
||||||||
|
X |
||||||||
|
X |
Rezultatele celor 20 de experimente : 17 din ele ofera comunicatia 1 cu 5.
Probabilitatea acestui eveniment se estimeaza ca fiind:
![]()
Este evident ca procedura este expeditiva, iar introducerea si procesarea datelor este facila.
Studiu de caz (3) Stabilirea configuratiei unei retelei de transport pe sine
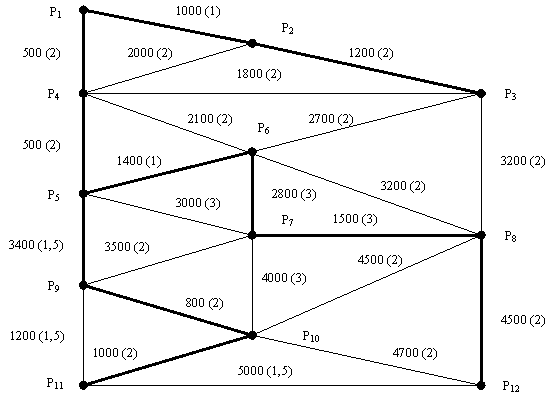
Fie urmatoarea dispunere a 11 unitati urbanistice (P2.P12) - fig. 3 - care trebuie conectate la un punct central (P1 - reprezentarea depoului de tramvaie) printr-o retea care sa satisfaca in primul rand conditia de lungime cat mai redusa, dar si alte considerente tehnico-economice (de exemplu, cheltuielile totale in functie de costul metrului liniar de linie - ca variabila dependenta de structura solului - sa fie minime). Configuratia a tinut cont de amplasarea punctelor de polarizare a interesului publicului, de pozitia celorlalte constructii si instalatii existente etc., astfel ca schema legaturilor posibile poate fi considerata fezabila.
Utilizand algoritmul lui Kruskal se determina configuratia minima astfel:
Pas 1. Se alege din multitudinea de arce, acela care are valoarea cea mai mica;
Pas 2. Din cele ramase se alege urmatorul in ordinea marimii si care nu formeaza ciclu cu cel ales deja;
Pas 3. Se repeta pasul 2 pana cand se determina arborele minimal.
Arborele minimal determinat se identifica ca avand 18800 m - cu linie ingrosata in fig. 3.
Reteaua comporta insa si o tratare din punct de vedere al asigurarii unor cheltuieli reduse pentru constituirea tronsoanelor propriu-zise, corespunzator rezistentei solului (tinand cont ca aceste cheltuieli depind atat de lungimea traseului cat si de capacitatea de sustinere a terenului). In fig. 3 , in dreptul fiecarui arc al retelei, este precizat costul unitar pentru constructia caii.
 Dificultatea este ca pana la procurarea mijloacelor materiale pentru
lucrare, preturile vor fluctua. Se pune intrebarea : exista posibilitatea
demararii lucrarii pe unele tronsoane, care se manifesta ca un invariant din
punct de vedere al preturilor ? Pentru a primi raspunsul se imagineaza un
algoritm de simulare:
Dificultatea este ca pana la procurarea mijloacelor materiale pentru
lucrare, preturile vor fluctua. Se pune intrebarea : exista posibilitatea
demararii lucrarii pe unele tronsoane, care se manifesta ca un invariant din
punct de vedere al preturilor ? Pentru a primi raspunsul se imagineaza un
algoritm de simulare:
Fig. 3. Proiectul unei retele de linii de tramvai
se apreciaza ca exista urmatoarea corelatie posibila intre cost V si debit:
![]()
unde k este o constanta de stare calculata ca raport intre costul curent si costul de referinta;
se reconfigureaza amplasamentul metric al punctelor, fiecare arc al grafului avind alocata valoarea modificata, conform costului dat de relatia (8) - fig. 4.
reluarea algoritmului Kruskal conduce la o lungime a retelei de 33700 m, in conditiile abordarii problemei costului.
Se poate insa constata ca unele tronsoane ( P1-P2-P3 ; P1-P4-P5-P9 ; P5-P6 ; P7-P8 ; P9-P10) sunt prezente in ambele ipoteze.
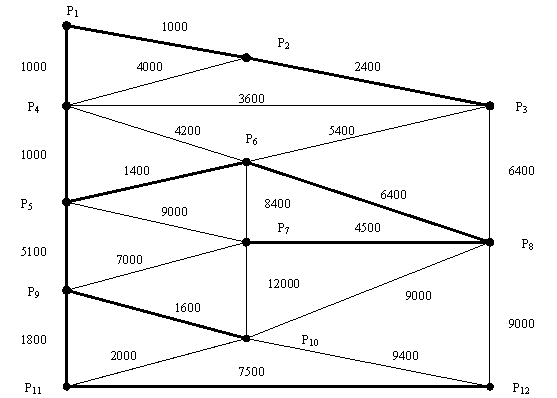
Fig. 4. Reconfigurarea retelei de linii de tramvai
Deci, simularea situatiei alternative recomanda lucrarile pentru tronsoanele mentionate, urmand ca la momentul oportun sa se discearna intre variantele ramase P6-P7 si P9-P10-P11 sau P6-P8 si P9-P11-P12.
3. Breviar teoretic al simularii
Studiul unui sistem se deruleaza pe parcursul mai multor etape:
(a) formularea problemei legate de sistem;
(b) crearea modelului sistemului (adica acea reprezentare partiala a carei calitate se estimeaza comparind comportarea modelului cu a sistemului real);
(c) obtinerea solutiei (optime) prin deducerea sau numai observarea evolutiei starilor modelului (totalitatea informatiilor produse de sistem constituie solutia; procedeul de obtinere a ei in functie de conditiile initiale, formeaza metoda de solutionare a modelului).
Pentru rezolvarea unor sisteme se poate alege calea simularii. In continuare prin simulare se va intelege simularea numerica (in opozitie cu simularea analogica care tine mai mult de modelism si probe materiale si nu a intrat inca suficient in atentia matematicienilor). Prin simulare numerica se intelege totalitatea procedeelor matematice si de calcul destinate studiului comportarii sistemelor reale in evolutia carora intervin si elemente aleatoare. Simularea numerica este o tehnica potrivit careia se asociaza sistemului real un model adecvat, ce descrie toate interactiunile logice ale componentelor, cat si mecanismul schimbarii lor in timp. Modelul de simulare permite crearea de experiente 'artificale' asupra sistemului, iar pe baza prelucrarii acestor experiente, sa se obtina raspunsurile referitoare la sistem.
Din punct de vedere teoretic se spune ca sistemul a simuleaza sistemul b daca si numai daca:
a si b sunt sisteme formale;
b este luat drept real;
a este considerat o aproximatie a sistemului real;
regulile de validitate din a nu sunt fara erori* .
Matematica simularii face apel la doua clase de elemente : elemente de intrare si elemente de iesire. Fiecare clasa contine mai multe variabile si o serie de parametrii (distinctia este urmatoarea : pe parcursul unei actiuni de simulare variabilele isi schimba valorile, in timp ce parametrii raman aceeasi pana la finele 'jocului'). Variabilele de intrare pot fi deterministe sau stohastice (cele deterministe pot fi obtinute dupa reguli bine precizate, cele stohastice sunt generate prin procedee specifice).
Simularea se desfasoara apoi in etape, in care mecanismul interior dirijeaza intrarile catre iesiri ; o etapa scurta in timpul executarii simularii, etapa in care toate variabilele de intrare iau valori constante, se numeste pas al simularii. Variabilele de iesire depind de intrari si de procesarea interna corespunzatoare fenomenului derulat. Dependenta este determinata de structura logica a modelului de simulare. O valoare a unei variabile de iesire este rezultatul executarii unui pas al simularii. Daca cel putin una din variabilele de intrare e stohastica, atunci cel putin una din variabilele de iesire este stohastica[1]. Dependenta logica intre variabile se poate (trebuie) sa fie ilustrata printr-o diagrama bloc (schema logica) a modelului de simulare. Aceasta diagrama trebuie sa precizeze conditionarile logice ale elementelor sistemului si operatiile aritmetice necesare. Deoarece prin insasi natura sa algoritmica, modelele de simulare au un caracter discret, simularea pe rand a schimbarilor sistemului ar putea sa conduca la un moment dat, la situatia in care diferite elemente ale sistemului au parcurs diferite intervale de timp. Astfel, prin descrierea comportarii sistemului, simularea este indisolubil legata de coordonata timp (nu doar in subsidiar ca in cazul modelelor rezolvate analitic).
In consecinta, algoritmul simularii contine un numar finit de operatii si aproape intotdeauna are definita o variabila numita 'ceasul simularii' care este supusa unui numar oarecare de cresteri pe parcursul simularii. Variabila in speta este necesara pentru a putea mentine ordinea corecta a tuturor evenimentelor. Exista doua tipuri de ceas:
(a) cu crestere fixa (in care dupa o incrementare se analizeaza situatia diferitelor elemente, generand toate evenimentele produse in intervalul constant scurs);
(b) cu crestere variabila (marimea cresterii este egala cu intervalul de la starea actuala la momentul aparitiei celui mai apropiat eveniment viitor).
Chiar daca problema care a condus la utilizarea simularii pentru solutionare nu pare una de proces in timp, legatura cu acest tip de coordonata spatio-temporala se mentine, intrucat timpul este o unitate de masura universala si limiteaza cel putin durata totala a simularii. Astfel, in unele cazuri drept criteriu de oprire a simularii se regaseste durata afectata actiunii in ansamblul sau (disponibilitatea de timp pentru aflarea rezultatului ; ca acest rezultat nu este 'chiar' cel exact poate sa conteze mai putin daca resursa timp s-a epuizat : de multe ori o solutie mai slaba este preferabila asteptarii indefinite a solutiei perfecte*). Chiar si in domeniul decelarii informatiile initiale (obtinerii datelor de intrare), viata impune o limita in interiorul careia se accepta ca s-a obtinut volumul si structura acestora, suficient de reprezentative pentru sistemul real.
In afara elementelor de intare si de iesire mentionate deja, modelele de simulare contin anumite relatii functionale (identitati si/sau ecuatii si/sau inecuatii) si caracteristici operative (ipoteze statistice sau nu):
(a) identitatile sunt afirmatii tautologice*** referitoare la componente ale modelului (de exemplu fixarea unui anumit nivel al stimulului pentru obtinerea unui raspuns din partea sistemului);
(b) caracteristica operativa este de obicei o ipoteza care leaga variabilele sistemului (de exemplu, media exprimata numeric a unui fenomen, insotita de o deviatie, leaga variabila identificata de domeniul simularii).
O componenta majora a simularii o reprezinta institutia metrologica : observatiile si masuratorile sunt indispensabile pentru estimarea caracteristicilor modelului si fac posibila validarea acestuia ; simularea nu poate fi in nici una din ipostazele sale asemuita 'cutiei negre'. Mai mult, simularea poate fi considerata gata de folosire abia dupa verificarea de ansamblu a functionarii ei prin teste de concordanta.
Daca se stie ''sigur'' ca la o anumita structura a datelor de intrare, sistemul real da un raspuns cunoscut, atunci la aceesi structura a variabilelor si parametrilor de intrare, simularea trebuie sa ofere un raspuns echivalent.
Daca insa simularea este utilizata euristic , atunci prin intermediul simularii se pot face experiente pe model luand conditii initiale arbitrare : in aceste cazuri obtinerea informatiilor despre sistem, chiar inainte ca acesta sa aiba la dispozitie intreaga gama de date, transforma simularea intr-un instrument util pentru proiectare si previziune.
Desi din punct de vedere al gradului de abstractizare simularea nu poate fi considerata de acelasi nivel cu alte capitole ale matematicii, simularea este utila, afirmatia bazandu-se pe constatarea ca aproape nu exista proiect de anvergura a carui realizare (sau macar validare a lui) sa nu se bazeze, intr-o anumita masura, pe aceasta tehnica.
4. Generarea numerelor aleatoare
Deoarece in evolutia lor sistemele reale sunt infuentate si de factori aleatori, al caror efect trebuie pus in evidenta de modelul de simulare, una din problemele modelarii este obtinerea unor astfel de numere (si mai mult, asigurarea ca repetabilitatea testului este posibila). O afirmatie de tipul 'numarul 3 este intamplator' nu are sens daca nu este plasata intr-un context statistic. Dar un sir de numere intamplatoare, care pot fi incadrate intr-o repartitie de probabilitate specifica, reprezinta un exemplu de numere aleatoare. De pilda, sirul : 0,1; 0,7; 0,2; 0,3; 0,9; 0,6; 0,5; 0,8; 0,9; 0,3 ; se bucura de proprietatea de a fi reparizat aproape uniform intre 0 si 1. Astfel, o selectie intamplatoare de numere care acopera nepreferential un domeniu pozitiv ce poate fi normat , reprezinta rezultatul unei actiuni de generare a numerelor aleatoare.
Numerele aleatoare uniforme pe intervalul unitate sunt cele mai importante elemente ale simularii numerice. Determinarea lor este o problema capitala pentru simulare. Desi exista procedee fizice si tabele cu numere intamplatoare extrase din diferite forme de recensaminte (anexa I ), totusi procedeele aritmetice sunt cele mai utilizate. Acestea se bazeaza pe formule de recurenta de tipul :
xn+1=fct(xn) (2)
alegerea lui x1 nefiind supusa nici unei conditionari prealabile. Trebuie precizat ca numerele perfect aleatoare nu pot fi generate prin procedee expeditive (ce vor fi expuse, pe scurt in continuare). Numerele pseudoaleatoare se pot obtine astfel:
(a) procedeul ridica la patrat a unui numar de 4 cifre cu pastrarea succesiunii centrale si reluarea operatiei, (tab 5).
Tab. 5 Procedeul generarii numerelor alatoare prin ridicare la patrat
|
Nr. |
X |
X2 |
Numere aleatoare |
In general succesiunea degenereaza dupa un numar finit de pasi. Lungimea perioadei depinde de numarul initial si poate ajunge, exceptional, la 104 numere.
(b) metoda congruentiala liniara:
xn+1=(a*xn +b)(mod c) (3)
adica restul impartirii primei paranteze, a*xn +b , la c .
unde, de exemplu, pentru a =5 ; x1=100 ; b=3 ; c=103 , se obtine sirul:
91 46 27 35
24 20 0 3 etc.
Lungimea perioadei depinde de numerele a, b, c alese initial (si poate ajunge la 107). Exista insa si pericolul ca numere alese neadecvat sa conduca la ciclare.
Practic, repartitia uniforma - notatia curenta este U(0,1) - reprezinta aparitia 'aproape' regulata a unor evenimente (transpunerea in realitate a valorilor obtinute impune utilizarea unei curbe de transformare - in acest caz, o dreapta). Daca aparitia evenimentelor reale este departe de a fi una regulata, este necesar sa se apeleze la o curba de transformare adecvata, in locul dreptei mentionate. Obtinerea numerelor aleatoare cu repartitie oarecare, de exemplu normala:
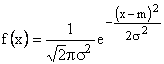 (4)
(4)
este mai complicata, dar nu insurmontabila. In unele abordari, pentru a obtine numere aleatoare distribuite normal, trebuie doar convertite numerele aleatoare distribuite uniform, modalitatea sugerindu-se in fig. 5.

Fig. 5 Functia de repartitie Gauss
Una din abordarile procedurale pentru elaborarea numerelor aleatoare de repartitie normala, utilizeaza teorema limita centrala si cuprinde mai multe etape.
In prima etapa, se face apel la relatia:
Z = ![]() (5)
(5)
unde Z este numarul aleator ce face parte din multimea cautata, adica repartizat dupa functia normala N(0,1) - in notatie curenta, media este 0 iar deviatia este 1.
In cea de a doua etapa, se transforma numarul Z in numar utilizabil in realitate X conform ecuatiei:
X = Z*![]() + m (6)
+ m (6)
in care m si
![]() sunt media si deviatia fenomenului din
realitatea ce se supune simularii.
sunt media si deviatia fenomenului din
realitatea ce se supune simularii.
Procedura se incheie dupa repetarea etapelor mentionate, de cite ori este necesar pentru obtinerea multimii de numere aleatoare, suficiente numarului de experiente preconizat. In anexa II este prezentata o lista de numere aleatoare repartizate normal.
Pentru repartitia exponential negativa de parametru l (foarte des intalnita in procesele de asteptare) densitatea de probabilitate este:
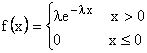 (7)
(7)
Cea mai lesnicioasa metoda de generare a unei variabile aleatoare care se supune acestei legi este de a inversa functia de repartitie:
![]() (8)
(8)
de unde:
![]() (9)
(9)
Cu alte cuvinte : daca se genereaza numere aleatoare uniform repartizate pe (0,1) si anume wn se obtin numere aleatoare xn repartizate exponential negativ, utilizind relatia (16) in care x devine xn iar w devine wn . In anexa III este prezentata o lista de numere aleatoare plasate exponential negativ.
5. Etapele abordari problemelor prin simulare
Daca se poate gasi o posibilitate de rezolvare analitica a problemei, atunci aceasta este intotdeauna de preferat, deoarece este mai exacta si de cele mai multe ori, necesita un efort mai mic decat alte conduite. Daca nu, si doar daca se pot invinge greutatile manevrarii algoritmului de procesare a datelor de intrare conform logicii interne a modelului, se poate lua hotararea de a se simula. Solutionarea care se intrevede prin aplicarea simularii se deruleaza, cel mai adesea, pe parcursul a trei faze:
(a) procesul de rezolvare;
(b) simularea propriu-zisa;
(c) procesul de prelucrare a datelor.
Folosirea eficace* si eficienta a simularii depinde in proportie covarsitoare de calitatea proceselor de rezolvare. Dar . nu poate fi (inca) indicat un catalog de metode de rezolvare (verificate), asa cum exista pentru procedeele analitice ale cercetarii operationale. Practicianul este constrans sa elaboreze pentru fiecare caz in parte un procedeu adaptat problemei aparute. Se pot insa scoate in relief puncte comune pentru mai multe metode deja incercate si validate:
majoritatea cailor de rezolvare sunt procede euristice;
procedeele folosite de simulare sunt expriente de orice fel;
in logica interna a simularii trebuie sa existe o functie-scop care ofera criteriul de oprire a experientelor;
de multe ori sunt utile reducerile de domeniu pentru variabile;
se face o alegere preliminara calificata a variantelor de start in special pentru parametrii;
se cauta sa se impuna o conduita de actiune ce conduce sistematic catre optim.
Simularea propriu-zisa inseamna efectuarea unui numar mare de calcule aritmetice si logice. Desi acest fapt conduce inevitabil catre utilizarea calculatoarelor, o testare facuta cu creionul si hartia este intotdeauna benefica (in acest context a simula inseamna a avea in derulare un program pentru calcul numeric).
Trebuie specificat ca parcurgerea unui pas al simularii se face in conditiile in care toate elementele care intervin sunt constante. Explicitarea afirmatiei este urmatoarea : in compunerea simularii exista un complex de relatii matematico-logice care stabilesc indubitabil starea urmatoare a intregului ansamblu.
Este necesar aici si acum sa se faca o distintie clara intre procesul de rezolvare si simulare : inexactitatile de care este afectat cateodata rezultatul, nu apar din cauza simularii propriu-zise, ci datorita procesului de rezolvare folosit.
Procesele prelucrarii datelor reprezinta veriga de legatura intre realitate si model, atat in etapa transformarii datelor initiale provenite din realitate in date de intrare necesare modelului de simulare, cat si in etapa de retransformare a rezultatelor gasite cu ajutorul modelului, intr-o forma care permite sustinerea afirmatiilor despre situatia reala.
Studiu de caz (4) Dimensionarea parcului de vehicule
In activitatile de productie (de exemplu, din transportul urban de calatori prin maxi-taxi), intr-o anumita masura aleatoare, utilizarea metodelor clasice de dimensionare a parcurilor de vehicule se poate dovedi citeodata inadecvata, conducand la rezultate care nu sunt de natura sa fie acceptate in practica. Se cere sa se determine strategia recomandabila in cazul unui transportator care are deja un numar de mijloace de transport, dar este la limita capacitatilor sale de acoperire a cererii. Alternativele posibile sunt:
refuzul - neacceptabil pentru ca se pierde clientela;
adaptarea - inchirierea unuia sau mai multor vehicule;
dezvoltarea - investitia in vehicule (achizitionarea de vehicule noi).
Solutia trebuie sa ofere numarul de vehicule suplimentare necesare si forma sub care sa fie utilizate.
Metoda de rezolvare ce se preconizeaza sa fie aplicata (pentru rezolvarea problemei se va utiliza metoda de simulare Monte Carlo), se bazeaza pe generarea unor valori ale cererii de transport si compararea acesteia cu valorile realizabile ale fiecarui vehicul si ale intregului parc in ansamblu. De ce sunt necesare numere aleatoare ? Pentru ca atat cererea cat si acoperirea ei, se supun zilnic, saptamanal, etc., unor variatii. Daca rezolvarea problemei s-ar face fara luarea in considerare a variatiilor mentionate, rezultatele nu ar fi concludente. Avand valorile cererii si realizarilor vehiculelor (de fapt avand legile care guverneaza aparitia valorilor numai in anumite limite si cu anumite deviatii de la medie) si experimentand pe mai multe situatii, se poate trage o concluzie asupra tendintelor, de principiu, ale activitatii si ofera conduita recomandabila pentru transportator. Evident, cu cat mai multe experimente, cu atat concluzia va fi mai aproape de realitatea concreta. Pentru aplicarea practica a acestor consideratii logice sunt necesare date istorice ale desfasurarii activitatii de transport in conditii concrete (cal*km).
Cu ajutorul acestora se vor determina media si deviatia cererii si productivitatii vehiculelor si se compara comportarea sistemului de transport in situatiile generate de cele 2 tipuri de date.
Principalele informatii sint legate de mediile si deviatiile fenomenelor care concura la caracterizarea situatiei. Valorile, pe zile ale saptaminii, sint prezentate in tab. 6.
Tab. 6 Realizarile medii ale vehiculelor (cal*km)
Ziua |
L |
Ma |
Mi |
J |
V |
S |
D |
|
Media | |||||||
|
Deviatia |
Datele necesare acestor calcule s-au colectat prin investigare completa timp de patru saptamini (s-au efectuat observari asupra activitatii de transport, rezultand datele statistice prezentate in tab. 7). Valorile se refera la numarul de cal*km efectuate de fiecare din cele 11 vehicule in uz (intr-un un interval de 24 ore).
Calculul abaterilor medii patratice s-a facut pornind de la dispersia de selectie:
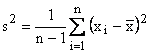
De exemplu,
abaterea medie patratica ![]() pentru ziua de luni s-a calculat cu
datele din tab 7 , astfel:
pentru ziua de luni s-a calculat cu
datele din tab 7 , astfel:
![]()
Aplicand relatia si celorlalte zile ale saptamanii, s-a obtinut tab. 6. Studiul statistic a aratat ca se poata admite ca numerele aleatoare (deci cal*km efectuati) urmeaza legea de repartitie normala.
Tab. 7 Realizarile de detaliu ale vehiculelor (date istorice)
|
Nr. |
Saptamana I |
||||||
|
Total | |||||||
Saptamana II |
|||||||
|
Total | |||||||
Saptamana III |
|||||||
|
Total | |||||||
Saptamana IV |
|||||||
|
Total | |||||||
|
Media zilnica |
54000+ 60000+ 60000)/ 4= 56800 |
72500+ 87000+ 81000)/ 4= 69725 |
53900+ 64400+ 33200)/ 4= 55775 |
82300+ 23000+ 78000)/ 4= 71575 |
71700+ 98000+ 24500)/ 4= 65050 |
80400+ 89000+ 57700)/ 4= 68025 |
52500+ 26000+ 67000)/ 4= 49675 |
Media numarului de cal*km efectuati de un vehicul intr-o zi este:
![]()
Calculul deviatiei, desi mai laborios, nu pune probleme ; abaterea medie patratica obtinuta este s
In continuare, se aplica metoda Monte Carlo pe o proba artificiala obtinuta cu ajutorul unui tabel de numere aleatoare, transformat intr-un tabel de abateri corespunzator repartitiei Gauss (anexa II). Se intocmeste tab. 8 care cuprinde numarul de cal*km de efectuat in 4 saptamani viitoare:
|
Ziua / Saptamana |
S1 |
S2 |
S3 |
S4 |
|
L Ma Mi J V S D |
Modul de calcul al coloanei S1 din tab. 8 este urmatorul:
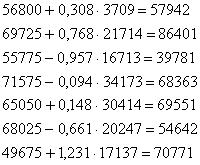
Cu ajutorul sirurilor alese pentru incercari (din anexa II ) se pot obtine realizari prezumtive corespunzatoare utilizarii a 5, 10 sau 15 vehicule.
Modalitatea de obtinere se exemplifica pentru 5 vehicule luate in considerare:
![]()
Coloana S1 din tab. 9, intocmit pentru cele de 5 vehicule, s-a obtinut astfel:

Tab. 9 Realizarile probabile (pentru 5 vehicule)
|
Ziua / Saptamana |
S1 |
S2 |
S3 |
S4 |
|
L Ma Mi J V S D |
Pentru definitivarea simularii, se trece la elaborarea unei metodologii de interpretare a seriei de rezultate obtinute. Se procedeaza in felul urmator (pentru saptamina 1 de simulare):
se coroboreaza informatiile din tab. 8 cu cele din tabelele de tipul celui prezentat mai sus (tab. 9 ; dar in mod asemanator si tabele pentru 10 , respectiv 15 vehicule luate in considerare);
pentru extragerea concluziilor, se calculeaza in coloanele 6 si 7 ale tab. 10 necesarul de mijloace suplimentare, respectiv inutilizarea acestora, datorita caracterului intimplator al activitatii;
relatiile au la baza o logica elementara:
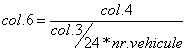
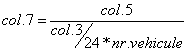
Tab. 10 Coroborarea datelor referitoare la sarcini si realizari probabile
|
Nr. vehicule |
Ziua |
Nr. cal*km de efectuat |
Capacitatea de lucru |
Prestatie neacoperita in timpul normat de lucru |
Disponibil de lucru |
Ore suplimentare |
Ore pierdute |
|
L Ma Mi J V S D |
|
||||||
|
Total | |||||||
|
L Ma Mi J V S D | |||||||
|
Total | |||||||
|
L Ma Mi J V S D | |||||||
|
Total |
tinind cont de conditiile de plata pentru orele suplimentare (200%), cu ajutorul valorilor din tab. 10 se poate obtine normarea rationala pentru minimul de ore:
5 vehicule * 7 zile * 8 h/zi + 1043*2 + 0 = 2366 h
10 vehicule * 7 zile * 8 h/zi + 288*2 + 83 = 1219 h
15 vehicule * 7 zile * 8 h/zi + 18*2 + 687 = 1563 h
aceste valori reprezentate grafic, conduc, dupa interpolarea obligatorie (prin intermediul unei curbe adecvate - de exemplu, tip parabola) la determinarea optimului si anume, 12 vehicule, fig. 6:
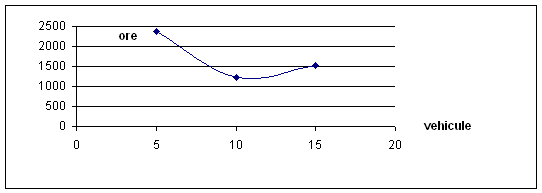 Fig.
6 Parabola de interpolare a valorilor cumulate ale orelor de munca
Fig.
6 Parabola de interpolare a valorilor cumulate ale orelor de munca
Actiunea se poate continua si pentru saptaminile 2, 3, 4 testate si va confirma justetea calculului : 12 vehicule vor greva mai putin bugetul de cheltuieli, decit cele 11 vehicule din structura actuala.
Studiu de caz (5) Determinarea calificarii fortei de munca pentru echipele de remediere a defectiunilor de pe teren
Intr-o subunitate de intretinere-reparatii se constata ca numarul defectiunilor la retea este o variabila aleatoare repartizata Poisson de parametru l=5 incidente/zi (repartitia Poisson se bucura de proprietatea ca intervalele intre aparitia defectiunilor urmeaza o lege de repartitie exponential negativa de parametru l). Costul nefunctionarii unui tronson al retelei este evaluat la 12 um/zi.
Administratia doreste sa decida intre organizarea unei echipe de reparatii care rezolva in medie 6 defectiuni pe zi si care costa 4 um/zi sau a unei echipe care rezolva in medie 8 defectiuni pe zi, dar costa 6 um/zi.
Se fac urmatoarele notatii:
Qn - duratele intre aparitia defectiunilor;
![]() - duratele de remediere ale defectiunilor (de asemenea
repartizate exponential
negativ);
- duratele de remediere ale defectiunilor (de asemenea
repartizate exponential
negativ);
C - costul unitar al nefunctionarii unui tronson al retelei (defectiune);
Ci - costul unitar al retribuirii echipei de reparatii,
in care i este numarul variantei (i= 1 echipa de mai mica eficacitate,
i= 2 echipa de mai mare eficacitate).
Conform celor prezentate, urmatoarele formule de recurenta genereaza sirurile de valori necesare variabilelor aleatoare Q si T :
![]()
![]()
![]()
unde:
m = 6 defectiuni remediate/zi;
m = 8 defectiuni remediate/zi.![]()
In relatiile de mai sus valorile ![]() si
si ![]() sunt doua siruri de numere aleatoare cu
repartitie uniforma intre 0 si 1 (si care sint luate din anexa III). Pentru
calculul duratelor de asteptare in cazul arcelor defecte, pana in momentul
repartitiei, se procedeaza astfel:
sunt doua siruri de numere aleatoare cu
repartitie uniforma intre 0 si 1 (si care sint luate din anexa III). Pentru
calculul duratelor de asteptare in cazul arcelor defecte, pana in momentul
repartitiei, se procedeaza astfel:
(a) daca se noteaza cu tf(n) durata de asteptare pina la remedierea de rang n atunci aceasta va fi egala cu durata de asteptare pina la inceperea remedierii si de reparare a defectiunii n-1 din care se scade durata Qn-1 dintre aparitia defectiunii n-1 si aparitia defectiunii n
![]()
in cazul in care: ![]()
in caz
contrar: ![]()
(b)
durata medie de asteptare in fir ![]() se calculeaza pentru numarul de situatii
simulate N cu relatia:
se calculeaza pentru numarul de situatii
simulate N cu relatia:
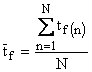
(c) durata medie de asteptare in sistem (inaintea reparatiei si in timpul ei) se calculeaza cu relatia:
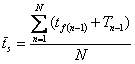
Constructia modelului se deruleaza astfel:
se porneste cu tf(1)=0 pentru n=1 deoarece prima defectiune intra imediat in reparatie;
se calculeaza apoi valorile de asteptare tf(n+1) pentru fiecare varianta;
pentru discernamant intre cele 2 variante, se vor calcula costurile totale de nefunctionare a componentelor retelei si a retribuirii echipei de reparatii;
cum durata totala de asteptare in fir
este 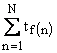 rezulta drept cheltuieli de nefunctionare:
rezulta drept cheltuieli de nefunctionare:
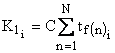
in acelasi fel, deoarece durata de
desfasurare a simularii este ![]() rezulta drept cheltuieli de retribuire:
rezulta drept cheltuieli de retribuire:
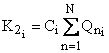
optimul va fi decis de:
![]()
Efectiv simularea se organizeaza cu ajutorul tab. 11, calculele fiind exemplificate imediat sub acesta:
Tab. 11 Simularea pe seria de probe agregate
|
Siruri de numere aleatoare uniforme [0-1] |
Durata intre defectiuni |
Duratele de remediere a defectiunilor |
Durata de asteptare in fir |
Durata de asteptare in sistem |
|||||
|
Nr.crt. |
|
|
Qn |
Tn1 |
Tn2 |
tf(n)1 |
tf(n)2 |
tf(n)1+Tn1 |
tf(n)2+Tn2 |
|
å | |||||||||
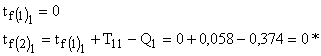
![]() .
. 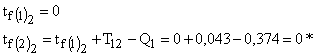
![]() .
.
Rezultatele obtinute sint urmatoarele :
![]()
interpretarea fiind evidenta : alegerea unei echipe eficiente este calea recomadata de simularea pe acest model.
6. Simularea de sistem
Simularea de sistem este sinonima construirii pe calculator a modelului dinamic al unui sistem complex si al functionarii sale. Sistemele simple pot fi cel mai adesea descrise in termeni matematici, de exemplu un sistem de ecuatii si inecuatii. Sistemele complexe nu pot fi descris analitic cu succes : exista interconditionari complicate, variabilele sunt neliniare, aleatoare sau isi schimba parametrii dupa reguli descriptive. Pentru aceste cazuri simularea este o buna alternativa. Dar simularea pe scara larga nu este posibila fara calculatoare. Diferentierea intre mai multe exemple de simulare apare cu pregnanta daca se ia in considerare modalitatea de schimbare a situatiei sistemului : daca sistemul isi modifica starea de la moment la moment, simularea este de tip continuu, de exemplu pentru studiile privind poluarea chimica a apelor, raspandirea bacteriilor si microbilor prin retele de alimentare cu apa, traiectoria de zbor a navetelor, etc. De obicei in cadrul acestui tip de simulare se manevreaza un sistem de ecuatii diferentiale care nu au solutii matematice, dar pentru care se pot indica directiile catre optimizare. Daca evenimentele care afecteaza sistemul sunt discrete, simularea este digitala, adica intre evenimente decelabile (separate) sistemul nu isi schimba starea.
Pentru primul caz exista limbaje, cum ar fi Continous System Modeling Program (CSMP) limbaje care pretind si un calculator analogic. Pentru al doilea caz exista limbaje, cum ar fi General-Purpose Systems Simulation (GPSS) limbaje care pretind un calculator obisnuit, numeric. In general toate limbajele de simulare pretind utilizatorului eforturi de 'calare' a problemei concrete pe structura antefixata de limbaj, deoarece aria limbajelor a fost scrisa initial pentru rezolvarea unei anumite probleme, a carei grad de generalizare poate sa lase de dorit. Fiind cel mai utilizat, acesta din urma - GPSS - va fi, foarte pe scurt, descris in continuare:
(a) limbajul are un algoritm de functionare care asigura:
un mecanism de inregistrare a timpului;
capacitatea de a prezenta incertitudinea;
posibilitatea de a evalua resursele sistemului;
facilitati de eliminare a erorilor;
accesibilitate usoara in dublu sens (intrari-iesiri);
(b) interpretarea impamantenita este aceea a unitatilor de trafic (tranzactii), care circula prin sistem si care interactioneaza cu alte unitati de trafic, in disputarea unor resurse (instalatii sau inmagazinari);
(c) limbajul isi descrie structura prin blocuri;
(d) algoritmul accepta ambiguitati in care ce priveste natura diferitelor entitati derulate (de exemplu, se poate specifica numai probabilistic ce se intampla cu o unitate intrata intr-un bloc, programul hotarand 'singur' calea de urmat).
7. Asupra necesitatii simularii
Nimic din sistemele reale nu se desfasora pur determinist sau in totalitate aleator. In principiu cele mai multe fenomene au o cauza obiectiva, uneori cunoscuta, alteori ramasa in afara cunostiintelor directe (cauza poate fi simtita prin intuitie sau dictata de experienta).
Nu trebuie insa sa se inteleaga ca practicianul se foloseste de simulare doar ca un instrument provizoriu de explorare a unor zone 'tulburi' in care cunoasterea nu a avansat suficient, zone ce vor fi abandonate legilor deterministe odata cu progresul stiintei. Marea majoritate a situatiilor care sunt studiate si rezolvate cu ajutorul simularii presupun prin insasi esenta lor o asemenea modalitate de abordare. In cazul multor fenomene foarte variate (economice, sociale, biologice) o aceeasi cauza nu are automat acelasi efect, iar necesitatea isi croieste drum printr-o multitudine de abateri individuale. Aceste fenomene sunt guvernate de legi statistice si ca atare nu pot fi studiate decat facand apel la probabilitati si simulare. Mai mult, fenomene despre care se credea ca sunt deterministe s-au dovedit dominate de statistica : studierea determinista a unor asemenea fenomene a dat rezultate multumitoare atata vreme cat stiinta experimentala, inca insuficient dezvoltata, nu a infirmat complet imaginea capatata despre ele (de exemplu, stabilirea sexului unor specii de reptile).
Analiza scoate in evidenta doua surse ale cauzelor fenomenelor:
(a) una are drept componenta principala tendinta generala (non-locala, determinista) a tuturor fenomenelor asemanatoare;
(b) alta are ca origine tendinta particulara (locala, aleatoare) specifica numai desfasurarii acelui fenomen (cercetat).
O exprimare posibila a acestei disocieri se poate face printr-o functie implicita:
![]() (10)
(10)
unde
![]() si t desemneaza pozitia
spatio-temporala a fenomenului;
si t desemneaza pozitia
spatio-temporala a fenomenului;
A - influenta generala;
B - influenta particulara,
intrucat orice fenomen este de fapt manifestarea unui proces mixt si dinamic.
Prin detaliere se pot obtine aproape toate situatiile intalnite in sistemele reale:
daca t = const. se obtin fenomene ce depind numai de suportul geometric;
![]() = const. defineste situatia proceselor
dinamice;
= const. defineste situatia proceselor
dinamice;
sistemele deterministe apar daca B identic zero;
sistemele aleatoare apar daca A identic zero.
Paradoxal, acest ultim tip de sistem este necesar pentru studierea celorlalte, atunci cand necunoasterea sau imposibilitatea cuprinderii realitatii persista, in ciuda incercarilor de a o reprezenta prin sisteme de alt tip decat cele determinate de hazard. Cu toate facilitatile oferite de modelarea fenomenelor, cu toate descoperirile matematicii, cateodata este imposibil de estimat pur analitic starile si evolutia sistemelor reale.
Nu in ultimul rind trebuie subliniata vitalitatea tehnicii numita simulare : daca doar una din multele conditii cerute de un sistem pur analitic nu se verifica, tot esafodajul matematic este inutil ; in schimb, in cazul simularii, se poate trece relativ usor peste aceste "amanunte" : simularea conduce catre rezultat indiferent de numarul si gravitatea inadvertentelor formale constatate. Acest fapt este echivalent cu afirmatia ca simularea a exploatat cu succes unul din punctele slabe ale matematicii : cautarea exactitatii extreme.
Omagiul cel mai potrivit care se poate formula in legatura cu simularea este cel explimat de Boll pe cind analiza ''certitudinile'' pe care le ofera hazardul : 'nimic nu este mai laudabil decit sa poti domina prin reguli, fenomene care depinzind de hazard, par sa nu admita nici o lege, sustragundu-se ratiunii umane'. Ori simularea ofera tocmai aceasta posibilitate.
Bibliografie
[1] Ackoff,R Bazele cercetarii operationale
Bucuresti Ed. Tehnica 1975
[2] Barbatu, Gh. Cercetarea operationala in intreprinderile industriale
Bucuresti Ed. Tehnica 1981
[3] Boll, M. Certitudinile hazardului
Bucuresti Ed. Stiintifica si enciclopedica 1978
[4] Constandache, G. Rationalitate, limbaj, decizie
Bucuresti Ed. Tehnica 1994
[5] Gattorna, J. Managementul logisticii si distributiei
Bucuresti Ed. Teora 2001
[6] Law, A. Simulation modelling and analysis
[7] Lupescu, T. Programarea matematica cu aplicatii militare
Bucuresti Ed. Militara 1965
[8] Marinescu, I. Elemente de statistica matematica si aplicatiile ei
Bucuresti Ed. Stiintifica 1969
[9] Maynard, H. Manual de inginerie industriala
Bucuresti Ed. Tehnica 1977
[10] Olaru, M Managementul calitatii
Bucuresti Ed. economica 1995
[11] Popoviciu, N. Strategii optime pentru probleme markoviene
Bucuresti Ed. academiei 1982
[12] Sacuiu, I. Numere aleatoare
Bucuresti Ed. academiei 1978
[13] Schatteles, T. Jocuri strategice si analiza economica
Bucuresti Ed. Stiintifica 1969
[14] Taniguchi, E. City logistics
[15] Teodorescu,N. Motode ale cercetarii operationale in intreprinderi
Bucuresti Ed. Tehnica 1972
[16] Vaduva, I. Modele de simulare cu calculatorul
Bucuresti Ed. Tehnica 1977
aleator- care depinde de o imprejurare nesigura (de o circumstanta necunoscuta si totala imprevizibila)
tehnica este, aici, notiunea ce inglobeaza totalitatea procedeelor intrebuintate in practicarea unei activitati
* simularea accepta existenta unor erori in mecanismul sau intern, deoarece a valida inseamna a verifica conditii cerute aprioric, ele insele fiind rezultatul unor operatii de acordare a valabilitatii (si care se supun acelorasi derulari de fapte)
Variabila stohastica : variabila ale carei valori nu pot fi stabilite decit pe baze statistice, cu ajutorul probabilitatilor (intrucit sint rezultatul unor fenomene prosuse intimplator).
insasi simularea este o solutie mai slaba pentru anumite probleme ale sistemelor reale carora nu li s-a putut inca descoperi total mecanismul intern sau carora nu li s-au putut rezolva pe cale analitica sistemele de relatii care exprima legaturile intime
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3478
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved