Arhitectura 8086 - Moduri de adresare

1.1 Introducere. Necesitatea limbajului de asamblare

Limbajul de asamblare (ASM) permite intelegerea la nivel de amanunt a ceea ce se intampla in realitate intr-un calculator. Familiarizarea cu un asemenea limbaj este mai mult decat benefica pentru un programator, contribuind la eficienta programelor dezvoltate, indiferent de limbajul utilizat.

Exista mai multe motive pentru care programarea in ASM este necesara. Codul generat in ASM se executa in general foarte rapid. Unele module de program trebuie implementate in ASM datorita acestei viteze de lucru. Uneori, o parte a unui program este scrisa intr-un limbaj de nivel inalt, iar modulele critice sunt scrise ca proceduri ASM, apelate la randul lor de modulele de nivel inalt.

Pe de alta parte, exista situatii in care e nevoie de acces direct la dispozitive de intrare / iesire sau la locatii fizice de memorie, iar aceste operatii nu pot fi executate in unele limbaje de nivel inalt. De exemplu, la calculatoarele personale, programele TSR si rutinele de tratare a intreruperilor sunt aproape totdeauna scrise in ASM.

Pe scurt, limbajul de asamblare ofera viteze de executie si acces la hardware care nu pot fi disponibile (cel mai adesea) in limbajele de nivel inalt.

Un alt aspect important este cel al dezvoltarii de programe pentru echipamente dedicate. Nu toate programele executabile sunt destinate calculatoarelor de uz general. Dezvoltarea masiva a microprocesoarelor a facut ca acestea sa controleze in prezent functionarea celor mai diverse obiecte tehnice, de la masini de gatit sau de spalat rufe pana la echipamente de control industrial sau pentru comanda avioanelor. Toate aceste microprocesoare functioneaza pe baza unor programe si nu trebuie sa fii cine stie ce specialist ca sa-ti dai seama ca e putin probabil ca un program care controleaza un cuptor cu microunde sau un osciloscop sa fi fost scris in PASCAL sau in BASIC. De fapt, majoritatea programelor pentru asemenea echipamente dedicate sunt scrise in limbaj de asamblare, pentru ca, intr-un asemenea context, ceea ce conteaza este viteza de executie si volumul foarte limitat de memorie.

Pe de alta parte, nu toate microprocesoarele sunt de uz general. Exista microprocesoare specializate, destinate unor scopuri precise, cum ar fi procesoare de semnal, micro-controllere industriale, automate programabile etc. Pentru asemenea procesoare, nu se justifica (in general) dezvoltarea de compilatoare pentru limbaje de nivel inalt, programele fiind dezvoltate in limbajele specifice acestor procesoare, care sunt asemanatoare limbajelor de asamblare pentru procesoarele de uz general.

Exista si un puternic rol formativ al programarii in limbaj de asamblare. Un programator nu ajunge niciodata la un nivel superior (de expert), daca nu trece (macar o data in viata) prin dezvoltarea de programe ASM.

Cursul de fata isi propune sa ofere cititorului un mijloc de a-si insusi limbajul de asamblare pentru procesoarele din familia Intel (IBM-PC). Ca mediu de dezvoltare, este folosita familia de produse software Borland (Turbo Assembler, Turbo Linker si Turbo Debugger).

1.2 Notiuni introductive de hardware. Registre. Stiva

In ASM, calculatorul este vazut la nivelul hardware: adrese fizice de memorie, registre, intreruperi etc. Sunt necesare unele notiuni pregatitoare.

Unitatea de baza a informatiei memorate in calculator este bitul. Un bit reprezinta o cifra binara (de aici si numele, care e o prescurtare de la binary digit), deci poate avea valorile 0 sau 1. Modelul hardware corespunzator este acela de bistabil. Un bistabil este, deci, un circuit electronic cu doua stari stabile, codificate 0 si 1, capabil sa memoreze un bit de informatie.

Un grup de bistabili formeaza un registru. De exemplu, 8 bistabili formeaza un registru de 8 biti. Informatia care se poate memora intr-un asemenea registru poate fi codificata in binar, de la valoarea 00000000 (toti bitii egali cu 0), pana la valoarea 11111111 (toti bitii egali cu 1). Este usor de vazut ca numarul combinatiilor care pot fi memorate este 256 (2 la puterea a 8-a). In general, un registru de n biti va putea memora 2ⁿ combinatii distincte. Aceste combinatii se numesc octeti sau bytes (daca n = 8), respectiv cuvinte (daca n = 16, 32 etc.). La procesoarele din familia Intel, cuvintele sunt de 16 sau 32 de biti (putand exista si cantitati pe un numar mai mare de biti, dar toate multiplu de 8).

Memoria unui calculator este vazuta ca o succesiune de octeti. Fiecare octet are asociata o adresa de memorie. Pentru a putea adresa memoria, e nevoie de un registru de adrese, a carui lungime determina dimensiunea maxima a memoriei. Daca avem un registru de adrese de 8 biti, atunci vom putea adresa 2⁸ octeti de memorie. Procesorul 8086 are un registru de adrese de 20 de biti, deci poate adresa 2²⁰ octeti de memorie (sau 1 megaoctet de memorie). Zonele de memorie vor fi reprezentate grafic pe verticala, ca succesiuni de octeti sau cuvinte, de la adrese mici catre adrese mari.

O adresa cu semnificatie speciala este adresa instructiunii care se executa in mod curent. Toate procesoarele au un registru destinat acestui scop, numit contor program (Program Counter). Acest registru contine intotdeauna adresa instructiunii care urmeaza a fi executata.

O zona speciala de memorie este asa numita zona de stiva. Stiva este un concept abstract de structura de date, dar procesoarele dispun de instructiuni masina pentru operatii cu o asemenea structura de date. O zona de stiva este caracterizata de o adresa curenta (numita adresa varfului stivei), adresata printr-un registru numit SP (Stack Pointer, indicator de stiva). Operatiile de baza cu stiva sunt:

PUSH (X), care se poate descrie prin actiunile:

(SP) <- (SP) - 1

((SP)) <- X

POP (X), care se poate descrie prin actiunile:

X <- ((SP))

(SP) <- (SP) + 1

Notatia (SP) inseamna "continutul lui SP', iar ((SP)), "continutul locatiei de memorie adresate de (SP)'. Din analiza celor doua operatii, se vede ca structura de stiva este de tip "Ultimul Intrat, Primul Iesit' sau "Last In, First Out', adica ultima cantitate care a fost "impinsa' in stiva printr-o operatie PUSH va fi cea care se va extrage la urmatoarea operatie POP. La procesorul 8086, cantitatile transferate in stiva sunt cuvinte de 16 biti, deci adresa curenta a varfului stivei (continuta in SP) este adunata sau scazuta cu 2.

Stiva poate fi folosita explicit pentru salvari si refaceri de date. Ea este folosita implicit in mecanismul de apel de procedura. Cand se apeleaza o procedura cu numele PR, printr-un apel generic de forma CALL PR, se va da controlul (adica se va produce un salt) la prima instructiune a procedurii. Acest salt nu inseamna altceva decat ca in registrul contor program se va depune adresa primei instructiuni din procedura.

Se pune insa problema revenirii din procedura, la executia unei instructiuni generice RETURN. Controlul trebuie sa revina in programul apelant si sa se execute instructiunea de dupa apelul de procedura.

Acest fapt este posibil, deoarece la executia instructiunii CALL, inainte de a se executa saltul la procedura, se salveaza in stiva continutul contorului program (adica adresa instructiunii imediat urmatoare apelului de procedura). Instructiunea RETURN nu face altceva decat sa extraga aceasta adresa din stiva si sa o plaseze in contorul program, executia continuand cu instructiunea de dupa apelul de procedura. Acest mecanism este ilustrat in Figura 1.1.

Un program ASM (ca de altfel si unul in limbaj de nivel inalt) este organizat in trei spatii de memorie:

. spatiul (zona) de cod - acesta cuprinde instructiunile care compun programul sau codul;

. spatiul (zona) de date - acesta cuprinde datele statice definite in program (care se gasesc la adrese fixe);

. spatiul (zona) de stiva - acesta cuprinde stiva rezervata programului.

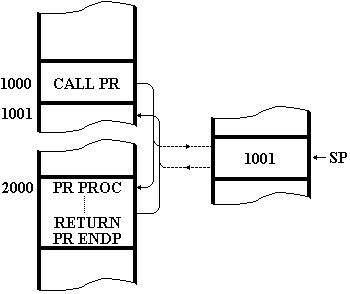
Figura 1.1 Rolul stivei la apelul unei proceduri

Zona de date poate fi detaliata in date constante, date initializate sau neinitializate etc.

Trebuie remarcat ca orice program executabil are structura de mai sus, indiferent de limbajul in care a fost scris, dar in ASM aceasta structura este vizibila si gestionata de catre programator. Acesta poate chiar schimba semnificatiile zonelor respective. De exemplu, exista situatii (programe TSR) in care datele sunt definite in acelasi spatiu de memorie cu instructiunile.

Pe langa cele trei spatii de memorie, mai exista si asa numitul spatiu de memorie disponibila. Acesta foloseste la alocari dinamice de memorie (la momentul executiei programului) si este gestionat in mod indirect, prin apeluri catre sistemul de operare.

1.3 Reprezentari interne ale datelor

1.3.1 Baze de numeratie

In tehnica de calcul, pe langa baza de numeratie 10, sunt folosite bazele de numeratie 2, 8 si 16, iar sistemele de numeratie respective se numesc binar, octal si hexazecimal. In sistemul hexazecimal, cifrele de la 10 la 15 se noteaza cu literele de la A pana la F. Tabelul 1.1 ilustreaza corespondenta dintre sistemele zecimal, binar, octal si hexazecimal. Trebuie retinut faptul esential ca, in memoria calculatorului, informatia de orice fel (date sau programe) este intotdeauna reprezentata in forma binara, deci ca secvente de cifre 0 sau 1.

Deoarece este greu de operat cu numere mari in baza 2, pentru exprimarea unor cantitati binare se folosesc bazele 8 si 16. De exemplu, numarul 255 se poate exprima in aceste baze prin 255₍₁₀₎ = 11111111₍₂₎ = ff₍₁₆₎ = 377₍₈₎.

Informatia este organizata in calculator pe grupe de cate 8 cifre binare (biti). Un asemenea grup se mai numeste si octet (sau byte). Octetul este unitatea de masura in care se exprima volumul memoriei unui calculator.

Deoarece dimensiunea memoriei este totdeauna o putere a lui 2, multiplii folositi pentru octeti nu sunt 100,1000 etc., ci puteri adecvate ale lui 2. Astfel, un numar de 2¹⁰ = 1024 de octeti se mai numeste si kilooctet sau kilobyte (pe scurt KO sau KB). Similar, un numar de 2²⁰ = 10264576 octeti se numeste megaoctet sau megabyte (MO sau MB). Se mai foloseste si gigaoctetul (gigabyte-ul), care este egal cu 2³⁰ octeti. Asadar, multiplii folositi in tehnica de calcul sunt:

.kilo = 2¹⁰ =1024

.mega = 2²⁰ =10264576

.giga = 2³⁰ =1073741824

Tabelul 1.1 Reprezentarea numerelor in bazele 10, 2, 8 si 16

1.3.2 Reprezentarea numerelor intregi

Numerele intregi pot fi reprezentate pe unul sau mai multi octeti, deci pe un numar n de biti. Deoarece fiecare bit poate lua doua valori (0 si 1), numarul total de valori distincte este 2ⁿ.

In cazul numerelor fara semn, valoarea interna a bitilor (octetilor) reprezinta chiar valoarea numarului. Este usor de vazut ca, daca reprezentarea este pe n biti, domeniul posibil de valori este de la 0 la 2ⁿ-1. Pentru n = 3 rezulta domeniul din Tabelul 1.2.

In ceea ce priveste reprezentarea numerelor cu semn, trebuie spus ca valorile interne care se pot reprezenta (deci configuratiile de biti) sunt aceleasi ca la numerele fara semn. Aceste configuratii variaza intre 00000000 (toti bitii egali cu 0) si 1111 1111 (toti bitii egali cu 1).

Se pune deci problema ca, printr-o conventie adecvata, sa se considere o parte din aceste configuratii de biti ca reprezentand numere intregi pozitive, iar cealalta parte numere negative.

Tabelul 1.2 Reprezentarea numerelor fara semn pe 3 biti

Exista mai multe sisteme de reprezentare, dintre care cel mai raspandit este sistemul de reprezentare in complement fata de 2. In acest sistem, bitul cel mai semnificativ joaca un rol special, anume de a preciza semnul numarului (din acest motiv se numeste bit de semn). Daca bitul de semn este 0, numarul reprezentat este pozitiv, iar daca bitul de semn este 1, numarul este negativ.

In ceea ce priveste valoarea absoluta (modulul) a numarului, ea se obtine diferentiat, functie de semnul numarului, in felul urmator:

. daca bitul de semn este 0, atunci configuratia interna reprezinta chiar valoarea numarului;

. daca bitul de semn este 1, atunci valoarea absoluta a numarului se obtine prin complement fata de

2, adica prin complementarea tuturor bitilor (0 devine 1 si reciproc) si prin adunarea apoi a valorii 1.

Aceasta regula se aplica pentru ambele sensuri de conversie (de la reprezentari interne la numere cu semn si reciproc).

De exemplu, fie numarul de biti n = 3 si sa consideram reprezentarea 111. Bitul de semn este 1, deci este vorba de un numar negativ. Prin complementare se obtine 000, iar prin adunare cu 1 se obtine 001, adica valoarea absoluta 1. Astfel, reprezentarea binara 111 pe 3 biti corespunde numarului -1.

Reprezentarea in complement fata de 2 pe n biti are urmatoarele proprietati generale:

. domeniul de reprezentare este -2^n-1 2^n-1-1;

. exista o singura reprezentare pentru 0, anume 000000;

. bitul cel mai semnificativ este bit de semn;

. calculul valorilor absolute pentru numere negative se face prin aplicarea regulii complementului fata de 2.

In Tabelul 1.3 sunt ilustrate domeniile de valori pentru numere cu semn pe n = 3 biti.

Sa remarcam faptul important ca o aceeasi reprezentare interna poate avea semnificatii (interpretari) diferite, dupa cum se considera reprezentarea cu semn sau fara semn. De exemplu, valoarea interna 1010 este interpretata ca -6 in reprezentarea cu semn si ca +10 in reprezentarea fara semn pe 4 biti. Se vede ca diferenta dintre aceste doua valori posibile este chiar 2ⁿ (in cazul de fata 16).

De aici se poate deduce o alta regula pentru aflarea rapida a reprezentarii numerelor negative: se aduna 2ⁿ, iar valoarea obtinuta se reprezinta ca numar fara semn.

De exemplu, ca sa obtinem reprezentarea lui -120 pe 8 biti, adunam 256 si obtinem valoarea pozitiva 136. Reprezentarea lui 136 in baza 2 va fi atunci reprezentarea in complement fata de 2 a lui -120, adica 10001000 sau 88H.

Tabelul 1.3 Reprezentarea numerelor cu semn pe 3 biti

In diverse sisteme de afisare a datelor numerice, in care este folosita numai baza 10, se utilizeaza codificarea de tip BCD care inseamna "Zecimal Codificat in Binar' (in engleza, "Binary Coded Decimal').

In acest sistem, se reprezinta o cifra zecimala pe un grup de 4 biti (4 biti pot codifica 16 valori distincte, deci 6 valori nu vor fi folosite). Un octet va codifica deci 2 cifre zecimale. De exemplu, octetul cu valoarea 01011001 reprezinta codificarea BCD pentru numarul zecimal 59 (primul grup de 4 biti reprezinta cifra 5, iar al doilea grup cifra 9). Daca este necesar, se pot considera n octeti pentru memorarea a 2n cifre zecimale.

Calculatoarele dispun, de obicei, de instructiuni speciale pentru calcule in format BCD. Sunt unele probleme care trebuie avute in vedere, si anume operatiile de corectie care trebuie facute dupa (sau inaintea) operatiilor in BCD, deoarece nu toate cele 16 combinatii binare posibile sunt cifre BCD corecte.

Formatul BCD se mai numeste si BCD impachetat, pentru a-l deosebi de formatul BCD despachetat, in care se reprezinta o cifra BCD pe un octet. In terminologia firmei INTEL (reflectata in denumirile instructiunilor procesoarelor), formatul BCD despachetat este denumit (oarecum incorect) format ASCII. Justificarea denumirii este ca, prin adaugarea valorii 30H (codul ASCII al cifrei 0), se obtine codul ASCII al cifrei reprezentate de octetul respectiv.

Toate cele trei sisteme de reprezentare a numerelor intregi ilustreaza faptul ca datele din memoria calculatorului se pot interpreta diferit. Aceste interpretari sunt facute de programul care foloseste datele. De exemplu octetul 10010100 poate reprezenta numarul zecimal pozitiv 148, numarul zecimal negativ -108 sau numarul zecimal pozitiv 94, dupa cum se lucreaza cu sistemul de reprezentare fara semn, cu semn sau, respectiv, cu sistemul BCD.

Reprezentarea numerelor reale

Numerele reale (fractionare) se pot reprezenta in doua moduri distincte, care sunt numite reprezentare in virgula fixa si reprezentare in virgula mobila.

Reprezentarea in virgula fixa

In reprezentarea in virgula fixa, se considera un numar finit de cifre semnificative, atat pentru partea intreaga a numarului, cat si pentru cea fractionara. Considerand baza de numeratie b, n cifre pentru partea intreaga si m cifre pentru partea fractionara, un numar fractionar x se reprezinta prin expresia:

x = i_n.bⁿ++i₁.b¹+i₀.b⁰+f₁.b^-1++f_m.b^-m

in care cifrele i_{n .} i₀ reprezinta partea intreaga, iar cifrele f_{1 .} f_m reprezinta partea fractionara a numarului x. Cifrele sunt considerate in baza b. Un asemenea numar se scrie pozitional in forma:

i_n.i₁i_0.f₁.f_{m (b)}

(in tehnica de calcul, virgula se noteaza cu un punct). Exemple de astfel de numere fractionare pot fi:

1AB34.FF52₍₁₆₎ 1000110.11011₍₂₎

Intr-o reprezentare interna concreta (pe un sistem de calcul), baza b si numarul de cifre de la stanga si de la dreapta virgulei (n si m) sunt fixate aprioric. De exemplu, lucrand cu baza 10 si presupunand ca o precizie de 0.001 este suficienta, se vor memora doar 3 cifre dupa virgula. Similar, daca se presupune ca numerele care trebuie reprezentate nu depasesc valoarea 10000, se vor

aloca 4 cifre la stanga virgulei. Se vor reprezenta astfel numere zecimale in domeniul 0.001 9999.999, cu o precizie de 0.001.

Cifrele respective vor fi numite mii, sute, zeci, unitati, zecimi, sutimi, miimi etc. si se vor reprezenta fie pe cate un octet, fie pe cate 4 biti. Memorarea semnului unui astfel de numar se face intr-un camp separat. Tabelul 1.4 exemplifica reprezentarea in virgula fixa a numerelor 1.013, -1230.192 si 10.000.

Tabelul 1.4 Reprezentarea in virgula fixa (b = 10, n = 4, m = 3)

Se observa ca punctul zecimal nu se reprezinta, deoarece pozitia sa este cunoscuta (este fixa, intre coloanele unitatilor si ale zecimilor). De altfel, numele metodei de reprezentare provine de la aceasta proprietate.

Uneori, se reprezinta numarul real respectiv inmultit cu 10 la o putere egala cu numarul de cifre de dupa virgula. De exemplu, numarul 1.013 se poate reprezenta intern ca numarul intreg 1013, iar numarul

-1230.192 ca numarul intreg -1230192 (in complement fata de 2, pentru a memora si semnul). In operatiile aritmetice care se vor face, se va tine seama de faptul ca numerele sunt inmultite cu 1000 si se va reprezenta punctul zecimal dupa a treia cifra de la dreapta la stanga.

Trebuie remarcat ca, intr-o astfel de reprezentare cu numar fix de campuri, nu se poate reprezenta decat un subset finit al numerelor reale, in exemplul de mai sus acest subset fiind cuprins intre -9999.999 si +9999.999, cu pasul 0.001. Trebuie retinut, de asemenea, ca toate valorile din subsetul respectiv sunt reprezentate exact.

De asemenea, este evident faptul ca operatiile aritmetice de inmultire si impartire se fac intr-un mod aproximativ. Inmultind 1.121 cu 2.250 se obtine valoarea teoretica 2.52225, dar aceasta nu se poate reprezenta in sistemul cu 3 cifre dupa punctul zecimal. Ca atare, rezultatul este rotunjit la valoarea cea mai apropiata care se poate reprezenta, anume 2.522. Operatiile de adunare si scadere se fac exact, cu conditia ca rezultatul sa nu depaseasca limitele domeniului de reprezentare.

In concluzie, reprezentarea in virgula fixa este caracterizata de numarul de cifre reprezentate si de numarul de cifre de dupa virgula (pozitia virgulei).

Reprezentarea in virgula fixa se foloseste in unele sisteme de conducere cu calculator a masinilor-unelte industriale (sisteme de pozitionare) si - foarte important - in sistemele de programe financiare si contabile.

La acestea din urma, reprezentarea in virgula fixa are avantajul ca toate puterile lui 10 (pozitive si negative) care fac parte din domeniul de valori sunt reprezentate exact.

De exemplu, pentru a reprezenta sume de bani, este suficient sa avem doua cifre dupa virgula. La un bilant financiar, cand se aduna sau se scad sume de bani, este esential ca operatiile de adunare si scadere sa se faca exact.

Din motivele prezentate, in programele aplicative pentru finante (in general pentru domeniul economic) se foloseste sistemul de reprezentare in virgula fixa.

Reprezentarea in virgula. mobila

Reprezentarea in virgula mobila se foloseste cu precadere in domeniile stiintifice si tehnice (sau, altfel spus, in toate domeniile in afara de cele economico-financiare).

In aceasta reprezentare, numerele sunt considerate de forma:

(-1)^S . M . B^E

unde:

. S este numit bit de semn si este 1 pentru numere negative si 0 pentru numere pozitive;

. M este numita mantisa (sau fractie) si este un numar pozitiv subunitar reprezentat in baza B;

. B este numita baza (uzual este 2 sau 16);

. E este numit exponent si este un numar intreg cu semn. Mantisa M se numeste normalizata daca prima cifra dupa virgula este cifra semnificativa (este diferita de zero).

Majoritatea sistemelor actuale folosesc baza B = 2. In acest caz, faptul ca prima cifra a mantisei este diferita de 0 inseamna ca aceasta este obligatoriu 1. Astfel, mantisa M verifica conditia (scrisa in baza 2):

0.1₍₂₎ ≤ M < 1

sau, in baza10:

0.5₍₁₀₎ ≤ M < 1

Exponentul se reprezinta de obicei deplasat, in sensul ca se memoreaza un numar de forma E + K, unde K este o constanta astfel aleasa incat E + K sa fie totdeauna pozitiv. In felul acesta se rezolva problema memorarii semnului exponentului. De cele mai multe ori, deoarece prima cifra semnificativa a mantisei M este 1, aceasta valoare nu se mai reprezinta, castigandu-se astfel un bit in spatiul de memorare (in care se poate memora bitul de semn S).

Cea mai des folosita reprezentare standardizata este cea numita in simpla precizie, descrisa in cele ce urmeaza. In acest sistem, mantisa M are 24 de biti, iar exponentul E are 8 biti si se reprezinta intern deplasat (adunat) cu 127. Mantisa este normalizata si inmultita cu 2, astfel incat conditia de normalizare este 1 ≤ M < 2.

Bitul cel mai semnificativ al mantisei nu se mai reprezinta intern, deoarece este totdeauna 1. Astfel, un numar real in simpla precizie se reprezinta pe 32 de biti (4 octeti).

Notand cu f mantisa (fractia) care se reprezinta intern, cu e exponentul deplasat si cu s bitul de semn, valoarea unui numar real este data de relatia:

(-1)^s 1.f₂₂ f₂₁ . f₁ f₀ 2^e-127

in care s este bitul de semn, e = e₇e₆ . e₁e₀ este exponentul deplasat cu 127, iar f = f₂₂ f₂₁ . f₁ f₀ este mantisa (fractia) normalizata. Bitul cu valoarea 1 din formula de mai sus (bitul 23 al mantisei) nu se reprezinta intern. Cei patru octeti sunt reprezentati in Tabelul 1.5, in ordinea asezarii lor in memorie (in sens crescator al adreselor de memorie).

Nu toate combinatiile posibile de biti din tabel sunt reprezentari valide. Astfel, numarul 0.0 se reprezinta in mod unic prin s = 0, f = 0 si e = 0, aceasta fiind singura valoare pentru care e sau f pot fi nule. In afara valorii reale 0.0, exponentul deplasat trebuie sa fie cuprins intre 1 si 254.

Exponentul 0 este permis numai pentru reprezentarea valorii reale 0.0 (deci si cu f = 0 si s = 0). Exponentul  255 (0FFH) este folosit pentru reprezentarea unor valori de exceptie. Astfel, reprezentarile cu e = 0FFH, f = 7FFFFFH (toti bitii 1) si s = 0 sau 1 sunt folosite pentru valorile notate +INF si -INF, care sunt cazuri de exceptie (depasiri aritmetice). Orice alte valori cu exponent 0 sau 255 sunt incorecte. Aceste valori incorecte mai sunt numite si NAN (de la Not A Number). Functie de bitul de semn, pot exista valori +NAN sau -NAN.

Tabelul 1.5 Reprezentarea in virgula mobila in simpla precizie

Alte valori reprezentative sunt:

. cel mai mic numar pozitiv reprezentabil este caracterizat de s = 0, f = 0, e = 1 si are valoarea aproximativa 1.17 10^-38;

. cel mai mare numar pozitiv reprezentabil este caracterizat de s = 0, f = 7FFFFF, e = 0FEH si are valoarea aproximativa 3.4 10³⁸.

Sa consideram cateva exemple de reprezentare.

. Numarul real 0.0 se reprezinta prin 4 octeti nuli.

. Numarul real 1 se exprima prin semnul s = 0, mantisa 1.0 si exponentul 0, (1 = (-1)⁰ 1.0 2⁰). Fractia interna este f = 0, iar exponentul deplasat este e = 127 (sau e = 7FH).

. Numarul real 2 se exprima prin semnul s = 0, mantisa 1.0 si exponentul 1, (2 = (-1)⁰ 1.0 2¹). Fractia interna este f = 0, iar exponentul deplasat este e = 128 (sau e = 80H).

. Numarul real 0.5 se exprima prin semnul 0, mantisa 1.0 si exponentul -1, (0.5 = (-1)⁰ 1.0 2^-1). Fractia interna este f = 0, iar exponentul deplasat este e = 126 (sau e = 7EH).

. Numarul real -1 se exprima prin semnul 1, mantisa 1.0 si exponentul 0, (-1 = (-1)¹ 1.0 2⁰). Fractia interna este f = 0, iar exponentul deplasat este e = 127 (sau e = 7FH).

Scriind bitul s, bitii fractiei f si ai exponentului deplasat e ca in Tabelul 2.4, se obtin reprezentarile pe 4 octeti de mai jos:

0.0 = 00 00 00 00 (s = 0, f = 0, e = 0)

1.0 = 00 00 80 3F (s = 0, f = 0, e = 7FH)

2.0 = 00 00 00 40 (s = 0, f = 0, e = 80H)

0.5 = 00 00 00 3F (s = 0, f = 0, e = 7EH)

. -1.0 = 00 00 80 BF (s = 1, f = 0, e = 7FH)

Reprezentarea in virgula mobila este caracterizata prin numarul de cifre al mantisei (fractiei) si numarul de cifre al exponentului.

Sa observam ca, la aceeasi mantisa, putem avea exponenti diferiti ceea ce inseamna ca virgula nu mai este pe o pozitie fixa, ci se deplaseaza dupa cat de mare este exponentul. Acest fapt a condus la numele reprezentarii (virgula mobila). Avantajul acestei reprezentari este domeniul toarte mare. In simpla precizie putem reprezenta numere cuprinse aproximativ intre -10³⁸ si 10³⁸.

Trebuie, de asemenea, remarcat ca se reprezinta corect numai numerele care se pot exprima ca sume de puteri (pozitive sau negative) ale lui 2 (in general ale bazei B). Exemplele de mai sus sunt din aceasta categorie. Numerele 0.1, 0.01, 0.3 nu se reprezinta exact in virgula mobila cu baza 2. De aceea, acest sistem nu se foloseste in programe pentru domeniile economico-financiare.

Calculele aritmetice sunt aproximative, dar precizia este de cele mai multe ori suficienta pentru aplicatiile uzuale. in reprezentarea in simpla precizie (pe 4 octeti), precizia asigurata este de 10^-7.

Reprezentarea in precizie dubla (8 octeti) este caracterizata de o mantisa normalizata pe 53 de biti si un exponent pe 11 biti (deplasat cu 1023). Valoarea unui numar real in dubla precizie este data de expresia:

(-1)^s 1.f₅₁ f₅₀ . f₁ f₀ 2^e-1023

in care s este bitul de semn, e = e₁₀e₉ . e₁e₀ este exponentul deplasat cu 1023, iar f = f₅₁ f₅₀ . f₁ f₀ mantisa (fractia) normalizata. Bitul cu valoarea 1 din formula de mai sus (bitul 52 al mantisei) nu se reprezinta intern. Structura celor 8 octeti (in ordinea crescatoare a adreselor) este cea din Tabelul 1.6 .

Valorile corecte pentru exponentul deplasat sunt cuprinse intre 1 si 1022. Numarul 0.0 se prezinta in mod unic cu s = f = e = 0, iar valorile cu exponent 1023 sunt folosite pentru +INF si -INF.

Tabelul 1.6 Reprezentarea in virgula mobila in dubla precizie

Reprezentarea in precizie extinsa (10 octeti) este caracterizata de o mantisa normalizata pe 64 de biti si un exponent pe 15 biti (deplasat cu 16383). Valoarea unui numar real in precizie extinsa este data de expresia:

(-1)^s 1.f₆₂ f₆₁ . f₁ f₀ 2^e-16383

in care s este bitul de semn, e = e₁₄e₁₃ . e₁e₀ este exponentul deplasat cu 16383, iar f = f₆₂ f₆₁ . f₁ f₀ este mantisa (fractia) normalizata. Bitul cu valoarea 1 din formula de mai sus (bitul 63 al mantisei) se reprezinta intern ca un bit totdeauna egal cu 1, cu exceptia valorii zero, cand acest bit este 0. Structura celor zece octeti (in ordinea crescatoare a adreselor) este cea din Tabelul 1.7.

Tabelul 1.7 Reprezentarea in virgula mobila in precizie extinsa

Microprocesoarele din familia 80x86 sunt dotate cu circuite specializate (coprocesoare matematice) care folosesc cele trei tipuri de reprezentari in virgula mobila de mai sus. De asemenea, limbajul de asamblare specific acestor procesoare dispune de directive pentru definirea de constante reale in toate cele trei precizii.

1.3.4 Reprezentarea datelor nenumerice

Pe langa date numerice, in memoria calculatorului trebuie reprezentate si alte tipuri de date. Un exemplu important il reprezinta caracterele alfabetice (litere mari si mici), caracterele numerice (cifre zecimale), semnele de punctuatie si asa-numitele caractere de control (folosite pentru comanda diverselor echipamente periferice).

Desi exista mai multe sisteme de codificare a acestor tipuri de date, pe majoritatea calculatoarelor actuale (inclusiv pe IBM-PC) se foloseste codul standard ASCII. Denumirea sa provine din initialele de la American Standard Code for Information Interchange (Codul Standard American pentru Schimb de Informatii).

Codul ASCII standard este un cod pe 7 biti, deci cuprinde 128 de caractere distincte. Un caracter ASCII se reprezinta pe un octet, in care bitul cel mai semnificativ este 0. Domeniul de valori este deci de la 0 la 127 (in zecimal) sau de la 00 la 7F (in hexazecimal).

Dintre cele 128 de caractere, 32 sunt caractere de control si nu au reprezentari grafice (nu sunt afisabile). Restul de 96 de caractere pot fi afisate pe ecranul calculatorului, la imprimanta etc. Caracterele afisabile se noteaza de obicei prin

scrierea simbolului grafic respectiv intre apostrofuri. De exemplu, 'A' inseamna codul ASCII corespunzator literei A mare,'!' inseamna codul ASCII pentru semn de exclamare etc.

Calculatorul IBM-PC lucreaza cu un asa-numit cod ASCII extins, in care se folosesc toti cei 8 biti ai unui octet. Setul ASCII standard este un subset al acestui cod ASCII extins.

Tabelul 1.8 cuprinde toate codurile ASCII. Coloanele corespund primei cifre hexa, iar liniile, celei de-a doua cifre. Primele doua coloane (in afara de codul 20H) si ultimul cod (DEL sau 7F) reprezinta cele 32 de caractere de control.

Deoarece caracterele de control nu au reprezentari grafice, ele au nume speciale (exprimate de obicei prin prescurtari de 2 sau 3 litere). Dintre caracterele de control uzuale, pot fi amintite:

. CR (Carriage Return). Este interpretat de perifericele de iesire, provocand mutarea cursorului pe ecran la inceputul liniei curente. La imprimanta, provoaca mutarea carului de tiparire la inceputul liniei;

. LF (Line Feed). Provoaca trecerea la linie noua (atat la imprimanta, cat si pe ecran);

. TAB (Horizontal Tabulation). Provoaca deplasarea cursorului pe ecran sau a carului de tiparire cu un numar predefinit de pozitii la dreapta sau intr-o pozitie predefinita;

. BS (Backspace). Provoaca deplasarea cursorului cu o pozitie inapoi (la stanga) sau stergerea caracterului de la stanga cursorului;

. DEL (Delete). Provoaca stergerea caracterului indicat de cursor;

. BEL (Bel). Provoaca emiterea unui sunet de avertizare;

. FF (Form Feed). Provoaca avansul hartiei (formularului) la pagina noua (la imprimanta).

O serie de coduri de control se folosesc in transmisiile de date, avand semnificatii specifice. De exemplu, ACK (Acknowledge) se foloseste pentru confirmarea transmisiei corecte a unui bloc de date, iar NAK (Negative Acknowledgement) pentru semnalarea unei transmisii incorecte.

Dintre caracterele tiparibile uzuale, se pot aminti:

. Literele mari 'A' 'Z'

. Literele mici 'a' 'z'

. Cifrele zecimale '0' '9'

. Spatiul (SP), care are codul 20H si este tiparit ca un spatiu liber (de fapt nu se tipareste nimic, ci se lasa o pauza); caracterul SP (spatiu,'') se numeste si blank.

Valorile numerice ale codurilor ASCII se exprima prin 2 cifre hexazecimale, in care prima cifra este limitata la 7F).

Tabelul 1.8 Codul ASCII standard

1.4 Tipuri de date utilizate in limbaj de asamblare

Limbajul de asamblare 80x86 opereaza cu anumite tipuri de date de baza. Aceste tipuri sunt recunoscute de catre procesor si fac parte integranta din formatul anumitor instructiuni masina. De asemenea, limbajul dispune de directive specifice pentru definirea acestor tipuri de date.

Caracteristic pentru un tip de date este domeniul de valori, care rezulta atat din tipul de date in sine, cat si dintr-o eventuala interpretare functie de context. Tipurile de date sunt:

BYTE (1 octet)

Acest tip de date ocupa 1 octet si poate fi reprezentat atat in memoria interna, cat si intr-un registru de 8 biti al procesorului. Interpretarile tipului byte pot fi:

. intreg pe 8 biti cu sau fara semn;

. caracter ASCII.

Directiva pentru definirea datelor de acest tip este DB (Define Byte).

WORD (2 octeti)

Acest tip de date ocupa 2 octeti si poate fi reprezentat atat in memoria interna, cat si intr-un registru de 16 biti al procesorului. Interpretarile tipului word pot fi:

. intreg pe 16 biti cu sau fara semn;

. secventa de doua caractere ASCII;

. adresa de memorie de 16 biti.

Directiva pentru definirea datelor de acest tip este DW (Define Word). Partea mai putin semnificativa este memorata la adrese mici. De exemplu, daca presupunem intregul 1234H la adresa 1000H, atunci octetul 34H se va gasi la adresa 1000H, iar octetul 12H la adresa 1001H. Similar, se memoreaza si secventele de doua caractere ASCII.

DOUBLE-WORD (4 octeti)

Acest tip de date ocupa 4 octeti si poate fi reprezentat atat in memoria interna, cat si intr-o pereche de registre de 16 biti sau intr-un registru de 32 de biti (la procesoarele de 32 de biti). Interpretarile tipului dword pot fi:

. intreg pe 32 de biti cu sau fara semn;

. numar real in simpla precizie;

. adresa de memorie de 32 de biti.

Directiva pentru definirea datelor de acest tip este DD (Define Double-Word). Valorile mai putin semnificative se memoreaza la adrese mici. In cazul adreselor pe 32 de biti, adresa de segment este memorata la adrese mari, iar deplasamentul (offsetul), la adrese mici.

QUAD-WORD (8 octeti)

Acest tip de date ocupa 8 octeti si poate fi reprezentat atat in memoria interna, cat si intr-o pereche de registre de 32 de biti (numai la procesoarele de 32 de biti). Interpretarile tipului qword pot fi:

. intreg pe 64 de biti cu sau fara semn;

. numar real in dubla precizie;

Directiva pentru definirea datelor de acest tip este DQ (Define Quad-Word).

TEN-BYTES (10 octeti)

Acest tip de date ocupa 10 octeti si poate fi reprezentat atat in memoria interna, cat si intr-unul din registrele coprocesoarelor matematice 80x87. Interpretarile tipului tbyte pot fi:

. numar intreg reprezentat ca secventa de cifre BCD (impachetate), cu semn memorat explicit;

. numar real in precizie extinsa.

Directiva pentru definirea datelor de acest tip este DT (Define Ten-Bytes).

In reprezentarea intregilor, se considera numere cu maxim 19 cifre zecimale. Un grup de doua cifre se reprezinta pe 1 octet, partea mai putin semnificativa fiind la adrese mici. In cadrul unui octet, cifra BCD mai semnificativa este in partea high a octetului. Cele 19 cifre BCD ocupa asadar 76 de biti. Ultimul grup de 4 biti (partea high a octetului aflat la adresa cea mai mare) este destinat memorarii semnului. De fapt, semnul se memoreaza doar pe bitul cel mai semnificativ al acestui ultim octet. Asambloarele accepta si numere cu 20 de cifre zecimale, atat timp cat cifra cea mai semnificativa, care se va reprezenta pe ultimul grup de 4 biti, nu intra in conflict cu bitul de semn.

Teoretic, valoarea maxima corect reprezentabila este:

iar valoarea minima este:

dar se accepta si valori de genul:

in care cifra cea mai semnificativa este reprezentata doar pe 3 biti.

Din motive de siguranta, este bine sa ne limitam la valorile garantate, adica la cel mult 19 cifre zecimale si semn.

Sa consideram urmatorul exemplu de program:

.model small

.data

b1 db -1, 10, 17H, 0FFH

b3 db 'a', 'b'

b2 db 'abcdef', 0

w1 dw 1234H, -1,'AB'

w2 dw w1

d1 dd 12345678H, -1

d2 dd 1.0, -1.0, 0.5

d3 dd d1

q1 dq 1000000000000002H, -1

q2 dq 1.0, -1.0

t1 dt 1234567890000012345

t2 dt -1234567890000012345

t3 dt 9999999999999999999

t4 dt -9999999999999999999

t5 dt 7999999999999999999

t6 dt -7999999999999999999

t7 dt 1.0

end

In acest exemplu, este definit doar un modul de date, folosind directivele si tipurile de date existente in limbaj. Liniile care incep cu un punct sunt directive care stabilesc modelul de memorie (.model) si, respectiv, definesc un segment de date (.data). Directiva end marcheaza sfarsitul programului.

Se definesc date cu cele 5 tipuri de directive (db, dw, dd, dq, dt), asociindu-se acestora si nume simbolice (b1, w2 etc.). Fisierul listing obtinut in urma asamblarii acestui program are (intre altele) urmatorul continut:

Turbo Assembler Version 2.0 03/31/96 23:08:59 Page 1

A.ASM

0000 .model small

0000 .data

0000 FF 0A 17 FF b1 db -1, 10, 17H, 0FFH

0004 61 62 b3 db 'a', 'b'

0006 61 62 63 64 65 66 00 b2 db 'abcdef', 0

000D 1234 FFFF 4142 w1 dw 1234H, -1, 'AB'

0013 000Dr w2 dw w1

10 0015 12345678 FFFFFFFF  d1 dd 12345678H, -1

11 001D 3F800000 BF800000+ d2 dd 1.0, -1.0, 0.5

3F000000

13 0029 00000015sr  d3 dd d1

15 002D 1000000000000002+  g1 dq 1000000000000002H, -1

FFFFFFFFFFFFFFFF

17 003D 3FF0000000000000+  g2 dg 1.0, -1.0

BFF0000000000000

20 004D 01234567890000012345 t1 dt 1234567890000012345

t2 dt -1234567890000012345

t3 dt 9999999999999999999

23 006B 89999999999999999999 t4 dt -9999999999999999999

t5 dt 79999999999999999999

25 007F F9999999999999999999 t6 dt -79999999999999999999

26 0089 3FFF8000000000000000 t7 dt 1.0

end

Prima coloana listeaza numarul liniei din fisierul sursa. Apoi este listata adresa si continutul campului de date corespunzator unei linii sursa. Daca acest continut este listat pe mai multe linii, se foloseste semnul + pentru a indica aceasta. Se remarca reprezentarile numerelor reale si ale intregilor negativi. Simbolurile r si s indica faptul ca este vorba de o adresa relativa (deplasament) sau de segment. De exemplu, variabila d3 contine adresa de segment 0000 si deplasamentul 0015H, adica adresa relativa (pe 32 de biti) a variabilei d1. La intregii BCD pe 10 octeti, se observa memorarea explicita a bitului de semn: reprezentarile pentru t1 si t2 difera doar prin acest bit.

Listingul nu indica si pozitia fizica a octetilor in memorie. Urmatorul listing reprezinta zona de memorie corespunzatoare modulului de date de mai sus:

ds:0000 FF 0A 17 FF 61 62 61 62 63 64 65 66 00 34 12 FF

ds:0010 FF 42 41 0D 00 78 56 34 12 FF FF FF FF 00 00 80

ds:0020 3F 00 00 80 BF 00 00 00 3F 15 00 68 53 02 00 00

ds:0030 00 00 00 00 10 FF FF FF FF FF FF FF FF 00 00 00

ds:0040 00 00 00 F0 3F 00 00 00 00 00 00 F0 BF 45 23 01

ds:0050 00 00 89 67 45 23 01 45 23 01 00 00 89 67 45 23

ds:0060 81 99 99 99 99 99 99 99 99 99 09 99 99 99 99 99

ds:0070 99 99 99 99 89 99 99 99 99 99 99 99 99 99 79 99

ds:0080 99 99 99 99 99 99 99 99 F9

Din examinarea acestui listing, se observa, de exemplu, reprezentarea interna a variabilei double-word d1, aflata la adresa 0015H: secventa de octeti este 78 56 34 12, deci la adrese mici se gaseste partea mai putin semnificativa. Similar, variabila de tip word 'AB' (aflata la adresa 11H), este memorata prin secventa de octeti 42H 41H. Acest listing este obtinut la incarcarea modulului de date in memorie, cand adresele de segment sunt relocate, deci corespund unor adrese fizice concrete. Adresa variabilei d1 (continuta in d3) apare aici in forma (5368:0015). Pentru valorile reale, se regasesc reprezentarile descrise in 1.3.3.

Variabila t1 (aflata la adresa 004DH) este reprezentata prin secventa de octeti: 45 23 01 00 00 89 67 45 23 01, deci cifrele mai putin semnificative sunt la adrese mici, iar in cadrul unui octet, cifra mai semnificativa este in partea high. Variabila t2 (aflata la adresa 0057H) este reprezentata prin secventa: 45 23 01 00 00 89 67 45 23 81, ceea ce arata ca bitul de semn (reprezentat prin cifra 8) este in partea high a ultimului octet din reprezentare.

Valorile maxime si minime sunt reprezentate la adresele 0061H si 006BH, prin secventele: 99 99 99 99 99 99 99 99 99 09, respectiv: 99 99 99 99 99 99 99 99 99 89.

Se observa si reprezentarea valorilor t5 si t6, in forma 99 99 99 99 99 99 99 99 99 79 si, respectiv, 99 99 99 99 99 99 99 99 99 F9, in care apare cifra cea mai semnificativa 7, cu bitul de semn 0 sau 1.

Trebuie precizat ca formatele de reprezentare pentru date numerice (intregi sau reali) se regasesc in aceeasi forma si in limbajele de nivel inalt.

In implementarea Borland PASCAL, exista caractere si intregi pe 2, 4 si 8 octeti, care corespund tipurilor de date byte, word, double word si quad-word. De asemenea, exista tipuri de date in virgula mobila pe 4, 8 si 10 octeti, in aceeasi forma de reprezentare interna ca cea descrisa in 1.3.3.

In implementarea Borland C exista tipul char (1 octet), tipuri intregi pe 2 si 4 octeti, cu sau fara semn (int, long, unsigned int, unsigned long) si tipuri in virgula mobila pe 4, 8 si 10 octeti (float, double, long double), cu aceleasi reprezentari interne ca cele din 1.3.3.

1.4 Arhitectura procesorului 8086. Formarea adresei fizice

Arhitectura procesorului 8086, din punctul de vedere al programului utilizator, este ilustrata schematic in Figura 1.2. Sunt figurate registrele accesibile prin program.

Figura 1.2 Registrele procesorului 8086

Toate registrele sunt de 16 biti. O serie de registre (AX, BX, CX, DX) sunt disponibile si la nivel de octet, partile mai semnificative fiind AH, BH, CH si DH, iar cele mai putin semnificative, AL, BL, CL si DL. Denumirile registrelor sunt:

. AX - registru acumulator

. BX - registru de baza general

. CX - registru contor

. DX - registru de date

. BP - registru de baza pentru stiva (base pointer)

. SP - registru indicator de stiva (stack pointer)

. Sl - registru index sursa

. Dl - registru index destinatie

Registrul notat FLAGS cuprinde flagurile procesorului sau ale bistabililor de conditie, iar registrul IP (instruction pointer) este contorul program.

Denumirile registrelor de segment sunt:

. CS - registru de segment de cod (code segment)

. DS - registru de segment de date (data segment)

. SS - registru de segment de stiva (stack segment)

. ES - registru de segment de date suplimentar (extra segment)

Se observa ca denumirile registrelor de segment corespund zonelor principale ale unui program executabil. Astfel, perechea de registre (CS:IP) va indica totdeauna adresa urmatoarei instructiuni care se va executa, iar perechea (SS:SP) indica totdeauna adresa varfului stivei. Registrele DS si ES sunt folosite pentru a accesa date.

Procesorul 8086 dispune de adrese pe 20 de biti, fiind capabil sa adreseze 1 megaoctet de memorie (2²⁰). Se pune problema cum se formeaza adresa fizica pe 20 de biti (deci pe 5 cifre hexa), deoarece toate registrele procesorului sunt de 16 biti, putand codifica adrese in domeniul 0000-0FFFFH (pe 4 cifre hexa), deci intr-un spatiu de maxim 64 KO.

Memoria unui sistem cu procesor 8086 este divizata in segmente. Un segment este o zona continua de memorie, de lungime maxima de 64 KO. Acest fapt inseamna ca ultima cifra hexa a adresei de inceput a unui segment este totdeauna 0. Ca atare, aceasta cifra se poate omite si adresa de segment se poate reprezenta tot pe 16 biti. Adresele de inceput ale segmentelor se vor gasi intotdeauna intr-unul din cele 4 registre de segment.

Adresarea in interiorul unui segment se realizeaza printr-un deplasament (offset) relativ la inceputul segmentului. Deoarece un segment nu poate depasi 64 KO, deplasamentul se poate memora tot pe 16 biti. Deplasamentul poate fi o constanta sau continutul unui registru care permite adresarea memoriei.

In concluzie, pentru adresarea unui octet de memorie, se folosesc doua cantitati pe 16 biti: o adresa de segment (continuta obligatoriu intr-un registru de segment) si un deplasament. Deoarece ambele cantitati sunt pe 16 biti, se vorbeste de adrese (sau pointeri) de 32 de biti, desi adresa fizica este doar pe 20 de biti.

Formarea adresei fizice (pe 20 de biti) este realizata automat (prin hardware) de catre o componenta a procesorului, conform Figurii 1.3.

Concret, adresa fizica se obtine prin deplasarea adresei de segment cu 4 biti la stanga si prin adunarea deplasamentului. Pentru specificarea unei adrese complete (de 32 de biti), se foloseste notatia (segment : offset) sau (registru_segment : offset). De exemplu, putem specifica o adresa prin (18A3:5B27) sau prin (DS:5B27).

Trebuie remarcat faptul ca asocierea (segment : offset) - adresa fizica nu este biunivoca, deoarece la o aceeasi adresa fizica pot sa corespunda mai multe perechi (segment : offset). De exemplu, perechile (18A3:5B27) si (18A2:5B37) reprezinta aceeasi adresa fizica. In situatia in care deplasamentul este redus la minim, adica in domeniul 0 F, corespondenta devine biunivoca. Adresele de acest tip se numesc adrese normalizate sau pointeri normalizati.

Figura 1.3 Formarea adresei fizice

O adresa completa de 32 de biti este memorata cu offsetul la adrese mici si cu adresa de segment la adrese mari. Adresele complete se pot obtine cu directiva DD (Define Double-Word).

Registrul de flaguri (bistabili de conditie) al procesorului 8086 are configuratia din Figura 1.4. O serie de flaguri sunt flaguri aritmetice: acestea sunt pozitionate la 0 sau la 1 ca urmare a unor operatii aritmetice sau logice. Celelalte flaguri controleaza anumite operatii ale procesorului.

Semnificatia flagurilor este urmatoarea:

. CF (Carry Flag, bistabil de transport) - semnifica un transport sau un imprumut din / in bitul cel mai semnificativ al rezultatului, de exemplu la operatii de adunare sau de scadere.

. PF (Parity Flag, flag de paritate) - este pozitionat in asa fel incat numarul de biti egali cu 1 din octetul cel mai putin semnificativ al rezultatului, impreuna cu flagul PF, sa fie impar; altfel formulat, suma modulo 2 a tuturor bitilor din octetul c.m.p.s. si a lui PF sa fie 1.

. AF (Auxiliarry Carry Flag, bistabil de transport auxiliar) - indica un transport sau un imprumut

din / in bitul 4 al rezultatului.

. ZF (Zero Flag, bistabil de zero) - este pozitionat la 1 daca rezultatul operatiei este 0.

. SF (Sign Flag, bistabil de semn) - este pozitionat la 1 daca b.c.m.s. al rezultatului (bitul de semn)

este 1.

. OF (Overflow Flag, bistabil de depasire) - este pozitionat la 1 daca operatia a condus la o

depasire de domeniu a rezultatului (la operatii cu sau fara semn).

Figura 1.4 Registrul de flaguri al procesorului 8086

. TF (Trap Flag, bistabil de urmarire) - daca este pozitionat la 1, se forteaza o intrerupere, pe un nivel predefinit, la executia fiecarei instructiuni; acest fapt este util in programele de depanare, in care este posibila rularea pas cu pas a unui program.

. IF (Interrupt Flag, bistabil de intreruperi) - daca este pozitionat la 1, procesorul ia in consideratie intreruperile hardware externe; altfel, acestea sunt ignorate.

. DF (Direction Flag, bistabil de directie) - precizeaza sensul (crescator sau descrescator) de variatie al dreselor la operatiile cu siruri de octeti sau de cuvinte.

Flagurile CF, PF, AF, ZF, SF si OF sunt numite flaguri aritmetice. Flagurile TF, IF si DF sunt numite flaguri de control.

1.5 Moduri de adresare

Pentru a scrie un program ASM intr-o forma cat mai simpla, se pot folosi directivele simplificate de definire a segmentelor. Acestea sunt:

. .model small (precizeaza un model de memorie)

. .code (definire de segment de cod)

. .stack n (definire de segment de stiva)

. .data (definire de segment de date)

. end eticheta (sfarsit logic al programului)

In principiu, segmentul de cod va cuprinde programul executabil (instructiuni), iar segmentul de date va cuprinde date definite de utilizator. Segmentul de stiva nu este folosit explicit. Comentariile se scriu folosind simbolul ;. Ceea ce urmeaza dupa ; pana la sfarsitul liniei curente este considerat comentariu.

Instructiunile procesorului 8086 pot avea unul sau doi operanzi, care pot fi registre sau operanzi aflati in memorie. Cand exista doi operanzi, unul este obligatoriu un registru (deci nu pot fi doi operanzi in memorie).

Modurile de adresare specifica modul in care se calculeaza adresa operandului aflat in memorie. Se folosesc denumirile de adresa de segment (AS) pentru adresa de inceput a segmentului in care se gaseste operandul si adresa efectiva (AE), pentru deplasamentul operandului in cadrul segmentului respectiv. Adresa de segment si adresa efectiva formeaza adresa fizica (AF), conform mecanismului descris in 1.4. Adresa de segment este furnizata de unul din cele 4 registre de segment.

Operanzii pot fi de tip octet sau de tip word, iar operatiile se pot face numai intre operanzi de acelasi tip. Tipul operandului aflat in memorie rezulta, de obicei, din context (din registrele folosite). In situatiile in care acest lucru nu este posibil, se foloseste operatorul ptr al limbajului de asamblare, in forma byte ptr sau word ptr, pentru a explicita tipul operandului.

. Adresare imediata

In acest mod de adresare, operandul apare chiar in instructiune. De exemplu:

mov ax, 1 ; Pune in AX valoarea 1

add bx, 2 ; Aduna 2 la BX

. Adresare directa

Adresa efectiva a operandului este furnizata printr-un deplasament in interiorul segmentului curent (vezi Figura 1.5).

.data

VAL dw 1

.code

mov bx, VAL ;Pune in BX continutul locatiei

;VAL in formatul instructiunii,

;expresia VAL se va inlocui cu deplasamentul

;in cadrul segmentului de date

add cx, [100] ;Deplasament explicit

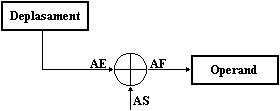
Figura 1.5 Adresare directa

Prima instructiune inseamna "pune continutul locatie VAL in BX', ceea ce va conduce la o valoare a registrului BX egala cu 1. A doua instructiune inseamna "aduna la CX continutul locatiei de memorie de la adresa efectiva 100'. De observat prezenta parantezelor drepte: fara ele, instructiunea ar fi insemnat "aduna valoarea 100 la registrul CX'. In ambele instructiuni, operandul aflat in memorie este considerat de tip word.

Acest mod de adresare foloseste registrul DS ca registru implicit de segment.

. Adresare indirecta (prin registre)

Adresa efectiva a operandului este data de continutul registrelor BX, Sl sau Dl (vezi Figura 1.6). Registrul implicit de segment este DS.

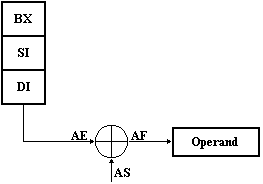
Figura 1.6 Adresare indirecta

in textul sursa se scrie, de exemplu:

mov ax, [bx] ; Pune in AX continutul

; locatiei de memorie de la

; adresa data de BX

mov [di], cx ; Pune continutul lui CX in

; locatia de la adresa data

; de DI.

add byte ptr ,[si], 2 ; Aduna 2 la octetul aflat la

; adresa data de SI

In primele doua instructiuni, operandul aflat in memorie este considerat de 16 biti (datorita celuilalt operand, care este un registru de 16 biti). Daca a treia instructiune ar fi scrisa;

add [si], 2

asamblorul nu ar sti tipul operandului din memorie. Instructiunea poate fi interpretata ca ,,aduna 2 la octetul de la adresa data de SI' sau ,,aduna 2 la cuvantul de la adresa data de SI' si s-ar obtine un mesaj de eroare la asamblare. Folosirea operatorului ptr elimina aceasta ambiguitate.

. Adresare bazata sau indexata

Adresa efectiva se obtine adunand la unul din registrele de baza (BX sau BP) sau la unul din registrele index (SI sau DI) un deplasament constant pe 8 sau 16 biti (vezi Figura 1.7). Registrul de segment implicit este DS (daca se folosesc BX, SI sau DI) si, respectiv, SS (daca se foloseste BP).

Forma de memorare a deplasamentului (pe 8 sau 16 biti) este determinata de asamblor. In textul sursa, se scrie pur si simplu un deplasament constant.

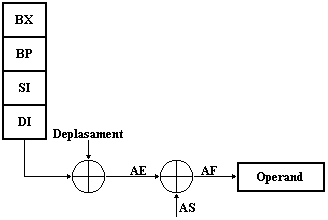
Figura 1.7 Adresare bazata sau indexata

Se pot folosi diverse forme de scriere, ca in exemplul de mai jos, in care bx este (din punct de vedere al mecanismului de adresare) adresa de baza, iar VAL este un deplasament constant. Din punct de vedere al programului, care isi propune sa acceseze elementele tabloului de octeti VAL, semnificatia este exact inversa: VAL este adresa de inceput a tabloului (deci o adresa de baza), iar bx este un indice (un deplasament).

.data

VAL dw 10 dup (0) ; Definire de tablou de 10

; octeti

. code

mov bx, 5

mov ax, VAL[bx]

mov ax, bx[VAL]

mov ax, [bx+VAL]

mov ax, [bx].VAL

Este posibil si alt mod de acces, in care se incarca registrul BX cu deplasamentul tabloului VAL (folosind operatorul offset) si se foloseste un indice explicit.

mov bx, offset VAL

mov ax, 5[bx]

mov ax, bx[5]

mov ax, [bx+5]

mov ax, [bx].5

In aceasta situatie, adresa de baza (continuta in BX) este adresa de inceput a tabloului VAL.

Trebuie remarcat ca, in textul sursa, toate formele de adresare se scriu cu operatorul de indexare (paranteze drepte). De exemplu, se poate scrie:

mov ax, [bx] ; Adresare indirecta

mov ax, [100] ; Adresare directa

mov ax, [bx+100] ; Adresare bazata

De remarcat ca folosirea registrului BP cu un deplasament nul permite o forma de scriere asemanatoare cu adresarea indirecta, dar codificata intern ca adresare bazata:

mov ax, [bx] ; Adresare indirecta

mov ax, [bp] ; Adresare bazata cu

; deplasament nul

. Adresare bazata si indexata

Adresa efectiva este formata prin adunarea unuia din registrele de baza (BX sau BP) cu unul din registrele index (SI sau Dl) si cu un deplasament de 8 sau 16 biti (vezi Figura 1.8).

Figura 1.8 Adresare bazata si indexata

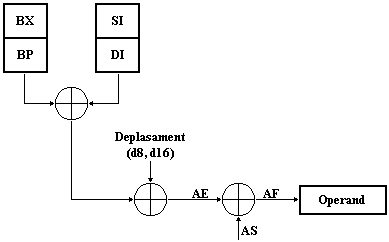
Registrele de segment implicite sunt DS (daca se foloseste BX cu Sl sau cu Dl) si, respectiv, SS (daca se foloseste BP cu Sl sau cu Dl). Deplasamentul poate fi si nul. In textul sursa se foloseste operatorul de indexare [ ]:

mov ax, [bx][si]

mov ax, [bx+si+7]

mov ax, [bx+si].7

mov ax, [bp][di][7]

In descrierea modurilor de adresare, s-a precizat de fiecare data registrul implicit de segment care participa la formarea adresei fizice a operandului aflat in memorie. Acest registru implicit este DS in toate modurile de adresare care nu implica registrul BP si, respectiv, SS, in modurile de adresare in care participa registrul BP.

Aceste reguli implicite pot fi modificate prin folosirea prefixelor de segment. Un prefix de segment este un octet care apare inaintea codului instructiunii masina si care identifica explicit registrul de segment folosit. in textul sursa, se scrie un registru de segment, urmat de :, inaintea operandului aflat in memorie:

mov bx, ds:[bp+7]

mov ax, cs:[si][bx+3]

mov ax, ss:[bx]

Evident, gestiunea a ceea ce se gaseste in segmentele adresate in acest fel cade in sarcina programatorului.

1.6 Codificarea interna a instructiunilor

Instructiunile procesorului 8086 pot fi codificate pe un numar de octeti cuprins intre 1 si 6. Codificarea cuprinde codul instructiunii (tipul operatiei), modul de adresare, deplasamentul operandului aflat in memorie (pe 8 sau 16 biti) sau adresa efectiva (in cazul adresarii directe), date (operanzi) imediate, pe 8 sau 16 biti. Pe langa formatul propriu-zis, mai poate exista un prefix de segment sau un prefix de repetare.

Formatul general al instructiunilor 8086 este ilustrat in Figura 1.9.

La instructiunile cu doi operanzi, un operand este obligatoriu de tip registru si este codificat de campul REG, iar celalalt este registru sau operand in memorie si este codificat de campul R/M sau de campurile R/M si MOD. Semnificatia campurilor din Figura 1.9 este urmatoarea:

. Campul D (destinatie) - codifica sensul operatiei:

D = 0 R/M <- R/M operatie REG

D = 1 REG <- REG operatie R/M

De exemplu, codificarile instructiunilor:

add [bx], si

add si, [bx]

vor diferi numai prin campul D (aceeasi operatie si aceiasi operanzi, dar difera sensul).

. Campul W (word) - codifica lungimea operanzilor (octet sau cuvant):

W = 0 operatie la nivel de octet

W = 1 operatie la nivel de cuvant

De exemplu, instructiunile:

add ax, bx

add al, bl

vor diferi doar prin campul W.

. Campul REG identifica operandul de tip registru.

. Campul R/M identifica al doilea operand de tip registru sau un registru care participa la formarea adresei efective a operandului aflat in memorie.

. Campul MOD codifica modul de adresare:

MOD =11 inseamna ca al doilea operand este tot de tip registru(codificat de campul R/M).

MOD = 00 inseamna adresare directa (R/M = 6), indirecta (R/M = 4, 5, 6) sau adresare bazata si indexata cu deplasament nul (R/M = 0,1, 2, 3). In aceste moduri de adresare, octetii 3 si 4 din Figura 1.9 lipsesc din formatul instructiunii (cu exceptia cazului R/M = 6, adica al adresarii directe).

MOD = 01 inseamna adresare bazata (R/M = 6, 7), indexata (R/M = 4, 5) sau bazata si indexata (R/M = 0, 1, 2, 3), toate cu un deplasament de 8 biti. In aceste moduri de adresare, octetul 4 din Figura 1.9 lipseste din formatul instructiunii.

Figura 1.9 Formatul instructiunilor 8086

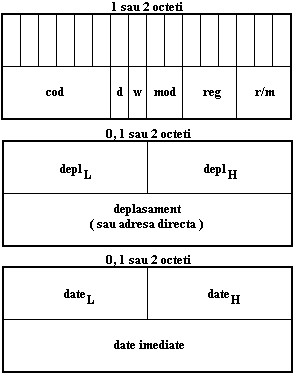
MOD = 10 este asemanator cu MOD = 01, dar deplasamentele sunt pe 16 biti. In aceste moduri de adresare, octetii 3 si 4 din Figura 1.9 sunt prezenti in formatul instructiunii.

Situatiile de mai sus sunt descrise sintetic in Tabelul 1.10.

Tabelul 1.10 Codificarea modurilor de adresare