| CATEGORII DOCUMENTE |
NOTIUNEA DE ARBORE Definitie.
Se numeste arbore un graf conex i fara cicluri.
Exemplu de arbore:
Graful G=(V,M) unde V= si M=, a carui reprezentare
grafica este figurate mai jos, este arbore:
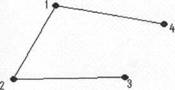
Demonstratie:
Graful prezentat mai sus este un arbore, deoarece este conex si fara cicluri.
Teorema. Fie G=(V,M) un graf. Urmatoarele afirmatii sunt echivalente:
a) G este un arbore.
b) G este un graf conex,
minimal cu aceasta proprietate (daca se
elimina orice
muchie, se obtine un graf neconex).
c)
G este fara cicluri, maximal cu aceasta proprietate
(daca se
adauga o
muchie, se obtine un graf care are cel putin un ciclu).
Exemplu: Pentru graful din figura de mai jos, se verifica foarte usor echivalenta afirmatiilor din teorema.
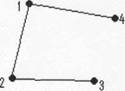
Demonstratie:
Graful este arbore (conex si fara cicluri).
Graful este conex, minimal cu aceasta proprietate, deoarece orice muchie s-ar elimina graful nu ar mai fi conex.
Graful este conex fara cicluri, maximal cu aceasta proprietate, deoarece orice muchie s-ar adauga graful ar contine eel putin un ciclu (urmariti figurile de mai jos)
|
|
|
|
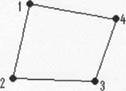
s-a adaugat muchia[4,3] s-a adaugat muchia[2 ,4] s-a adaugat muchia[l ,3]
Teorema. Orice arbore cu n>2 varfuri, contine cel putin doua varfuri terminale.
Demonstratie:
Presupunem ca exista un arbore A, cu n>2 varfuri, care contine un singur varf terminal; fie acesta x1.
Alegem in A cel mai lung lant elementar, adica lantul care contine numarul de muchii maxim posibil, care-l admite pe x, ca extremitate; fie acesta L=[ x,,x2 ,.,xp-1,xp]. Deoarece x1 este singurul varf terminal, inseamna ca xp
are gradul >2, deci pe langa nodul xp-1 mai este legat de cel putin un alt nod, fie
acesta y. Exista doua situatii:
a) y nu apartine lantului L, si atunci lantul nu ar fi cel mai mare deoarece s-ar mai putea prelungi cu muchia [xp,y]. Contradictie, deoarece am presupus ca L este cel mai lung.
b) y apartine lantului L, si atunci am putea scoate in evidenta
ciclul
[xp,y,.,xp-1,xp].
Contradictie, deoarece A este arbore, deci nu contine cicluri.

Contradictia provine din faptul ca am presupus ca A contine un singur varf terminal. In concluzie, A are cel putin doua varfuri terminale.
Teorema. Orice arbore cu n varfuri are n-1 muchii.
Demonstratie:
Demonstratia teoremei se realizeaza recurgand la principiul inductiei matematice.
Fie A un arbore cu n varfuri si A(n) numarul muchiilor acestuia. Enuntul teoremei cere sa se demonstreze ca A(n)=n-1.
I. Verificare
Daca n=l => A(n)=A(l)=l-l=0 Adevarat, deoarece arborele fiind format dintr-un singur nod nu are nici o muchie.
II. Demonstratia P(n) =P(n+l)
P(n) : A(n)=n-1
P(n+1) : A(n+1)=(n+ 1)-1
Cu alte cuvinte, daca se stie ca arborele cu n varfuri are n-1 muchii, trebuie sa se demonstreze ca un arbore cu n+1 varfuri are n muchii.
Fie A1 arborele cu n+1 varfuri, si xk un nod terminal al sau. Daca se
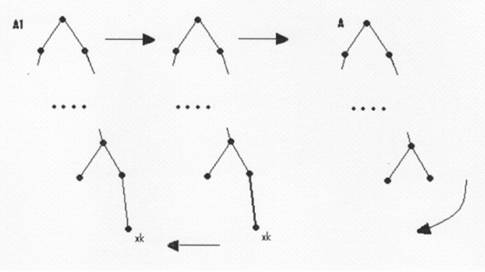
elimina
nodul xk si muchia incidenta
cu acesta se obtine un arbore A cu n varfuri care are, conform ipotezei, n-1 muchii.
Tinand cont de faptul ca A1 se obtine adaugand la A nodul si muchia eliminata tragem concluzia:
Arborele A1, cu n+1 noduri, are cu 1 mai multe muchii decat A, care are n-1 muchii, deci A1 are l+(n-l) muchii, adica n muchii.
Definitie. Fie G=(V,M) un graf. Graful G se numeste aciclic daca nu contine cicluri.
Definitie. Fie G=(V,M) un graf. Graful G se numeste padure daca nu contine cicluri.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2795
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved