| CATEGORII DOCUMENTE |
ALGORITMUL SIMPLEX
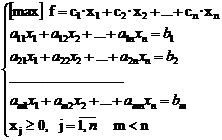

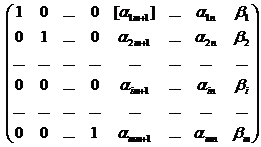
x B0 = ( b b ., bm, 0, ., 0 ) t si f (x B0 ) = c1 b + c2 b + . + cm bm

x B1 = 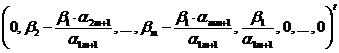
Avem ![]() si
si ![]() , i =
, i = ![]() rezulta a 1m+1 >0 si
rezulta a 1m+1 >0 si ![]() (raport minim)
adica trecerea de la o solutie de baza la alta solutie
de baza se face reducand o coloana cu respectarea conditiilor in
alegerea pivotului:
(raport minim)
adica trecerea de la o solutie de baza la alta solutie
de baza se face reducand o coloana cu respectarea conditiilor in
alegerea pivotului:
- elementul pivot trebuie sa fie pozitiv;
- daca in coloana care se reduce sunt mai multe elemente pozitive atunci pivotul va fi acela care furnizeaza cel mai mic raport cand termenii liberi se impart la elementele pozitive corespunzatoare, din aceasta coloana.
= ![]() c m+1 - (c 1 a 1m+1 + c 2 a 2m+1 + .+ c m a mm+1 )
c m+1 - (c 1 a 1m+1 + c 2 a 2m+1 + .+ c m a mm+1 )
d (c m+1 -f m+1) daca f m+1 = c 1 a 1m+1 + c 2 a 2m+1 +.+ c m a mm+1 = c BP m+1
Etapele algoritmului simplex sunt:
se imparte linia pivotului cu pivotul;
coloana pivotului va avea cifra 1 in locul pivotului si zero in rest;
elementele celorlalte coloane ale noului tablou simplex se determina folosind regula dreptunghiului.
1. anumite valori, adica xj = pj pentru un j dat;
2. valori in anumite intervale, adica pj xj qj, pentru un j dat.
Astfel de situatii sunt socotite modele sau probleme cu solutii impuse atunci cand restrictii precum cele mentionate sunt altele decat cele de semn.
max f = 4 x 1 +2 x 2 + 5 x 3 + x 4
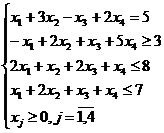
Pentru rezolvare construim tabelul simplex urmator:
|
cB |
B |
c |
|||||||
|
P1 |
P2 |
P3 |
P4 |
P5 |
P6 |
P7 |
b |
||
|
P6 P7 | |||||||||
|
P2 P6 P7 | |||||||||
|
P1 P2 P6 P7 | |||||||||
|
fj cj - fj | |||||||||
|
P1 P2 P3 P7 | |||||||||
|
fj cj - fj | |||||||||
|
P1 P2 P3 P5 | |||||||||
|
fj cj - fj | |||||||||
x opt = (1, 2, 2, 0) t, f max = 18.
x 5 = 2, x 6 = 0, x7 = 0.
DUALITATEA
Fie problema de programare liniara numita problema primala (1)
min f = cx
![]() (1)
(1)
Definitie Se numeste duala acestei probleme urmatoarea problema de programare liniara: max g = yb
![]() (2)
(2)
Teorema Are loc una si numai una din afirmatiile:
a) ambele probleme au solutii optime finite si atunci g max = f min
b) una dintre probleme are solutie infinita, iar cealalta problema nu are solutie (posibila) (este incompatibila)
c) una dintre probleme are solutie degenerata, iar cealalta problema poate avea solutii optime multiple.
Definitie Se numeste cuplu de probleme duale forma simetrica problemele urmatoare:
min f = cx max g = yb
![]() si (2)
si (2) ![]()
DIAGRAMA LUI TUCKER
|
PROBLEMA DUALA |
Variabile |
x1 |
x2 |
xn |
Relatii |
Constante |
|
|
yn+1 |
a11 |
a12 |
a1n |
b1 |
|||
|
yn+2 |
a21 |
a22 |
a2n |
b2 |
|||
|
yn+m |
am1 |
am2 |
amn |
bm |
|||
|
Relatii |
max g |
||||||
|
Constante |
c1 |
c2 |
cn |
min f |
x = (x1, x2, .. , xn) t - vectorul variabilelor primale de structura
x = (xn+1, xn+2, .. , xn+m) t - vectorul variabilelor primale de compensare
y = (y1, y2, .. , yn) - vectorul variabilelor duale de compensare
y = (yn+1, yn+2, .. , yn+m) - vectorul variabilelor duale de structura
In iteratia optima a tabelului simplex se afla componentele solutiilor ambelor probleme, adica:
|
cB |
B |
P1 |
Pn |
Pn+1 |
Pn+m |
b |
||
|
Componentele bazice ale solutiei optime a problemei primale |
||||||||
|
fj cj- fj |
fmin = gmax |
|||||||
|
Variabile duale de compensare |
Variabile duale de structura | |||||||
Exemplu Sa se rezolve problemele duale simetrice:
max f = 3 x1 + 5 x2 + 2 x3 min g = 6 y4 + 5 y5 + 7 y6
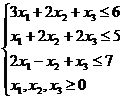
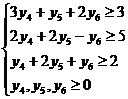
Rezolvare:
Vom rezolva, pe rand, cele doua probleme cu algoritmul simplex si apoi vom evidentia, in fiecare tabel si solutia optima a celeilalte probleme:
|
cB |
B |
3 |
5 |
2 |
0 |
0 |
0 |
c |
|
P1 |
P2 |
P3 |
P4 |
P5 |
P6 |
b |
||
|
0 0 0 |
P4 P5 P6 |
3 1 2 |
2 [2] -1 |
1 2 1 |
1 0 0 |
0 1 0 |
0 0 1 |
6 5 7 |
|
fj cj - fj |
0 3 |
0 5 |
0 2 |
0 0 |
0 0 |
0 0 |
0 - |
|
|
0 5 0 |
P4 P2 P6 |
[2] 1/ 2 5/2 |
0 1 0 |
-1 1 2 |
1 0 0 |
-1 1/ 2 1/ 2 |
0 0 1 |
1 5/2 19/2 |
|
fj cj - fj |
5/2 1/ 2 |
5 0 |
5 -3 |
0 0 |
5/2 -5/2 |
0 0 |
25/2 - |
|
|
3 5 0 |
P1 P2 P6 |
1 0 0 |
0 1 0 |
-1/ 2 5/4 13/4 |
1/ 2 -1/ 4 -5/4 |
-1/ 2 3/ 4 7/4 |
0 0 1 |
1/ 2 9/4 33/4 |
|
fj cj - fj |
3 0 |
5 0 |
19/4 -1/ 4 |
1/ 4 -1/ 4 |
9/4 -9/4 |
0 0 |
51/4 - |
|
Astfel solutia optima este: x opt = (1/ 2, 9/4, 0, 0, 0, 33/4 ) t, fmax = 51/4.
Solutia problemei duale este y opt = (0, 0, 11/4, 1/ 4, 9/4, 0 ), valori luate din linia cj - fj dar cu semn schimbat iar g min = 51/4.
Ne putem convinge de acest fapt prin rezolvarea directa a problemei duale:
|
bB |
B |
0 |
0 |
0 |
6 |
5 |
7 |
b |
|
Q1 |
Q2 |
Q3 |
Q4 |
Q5 |
Q6 |
c |
||
|
- - - |
- - - |
-1 0 0 |
0 -1 0 |
0 0 -1 |
[3] 2 1 |
1 2 2 |
2 -1 1 |
3 5 2 |
|
6 - - |
Q4 - - |
-1/ 3 2/3 1/3 |
0 -1 0 |
0 0 -1 |
1 0 0 |
1/3 4/3 [5/3] |
2/3 -7/3 1/3 |
1 3 1 |
|
6 - 5 |
Q4 Q5 - |
-2/5 2/5 1/5 |
0 -1 0 |
1/5 [4/5] -3/5 |
1 0 0 |
0 0 1 |
3/5 -13/5 1/5 |
4/5 11/5 3/5 |
|
6 0 5 |
Q4 Q3 Q5 |
-1/ 2 1/ 2 1/ 2 |
1/ 4 -5/4 -3/4 |
0 1 0 |
1 0 0 |
0 0 1 |
5/4 -13/4 -7/4 |
1/ 4 11/4 9/4 |
|
gi bi - gi |
-1/ 2 1/ 2 |
-9/4 9/4 |
0 0 |
6 0 |
5 0 |
-5/4 33/4 |
51/4 - |
|
Cum toate diferentele bi - gi 0, avem solutia optima g min = 51/4 cu yopt = (0, 0, 11/4, 1/ 4, 9/4, 0) respectiv pentru problema primala avem x opt = (1/ 2, 9/4, 0, 0, 0, 33/4 ) t, valori luate din linia bi - gi iar fmax = 51/4 = g min . Se vede, intr-adevar, ca s-au obtinut aceleasi solutii.
Algoritmul simplex dual
Exista situatii cand prin inmultirea unor restrictii cu (-1) apar in tabel vectori ce pot fi considerati in baza, caz in care se adopta o metoda putin modificata fata de algoritmul simplex. De fapt este vorba de aplicarea algoritmului simplex, dar asupra problemei duale. Etapele sunt aceleasi, dar, daca in coloana b exista elemente negative, atunci alegerea elementului pivot se va face respectand urmatoarele doua conditii:
- pe linia elementului negativ din coloana b se alege element pivot negativ;
- daca sunt mai multe elemente negative pe aceasta linie atunci pivotul va fi acela care furnizeaza cel mai mic raport, in valoare absoluta, dar considerat fata de elementele corespunzatoare din
linia c j - f j.
Exemplul Sa se rezolve, folosind algoritmul simplex dual urmatoarea problema de programare liniara:
min f = 4 x1 + 5 x2 + 3 x3
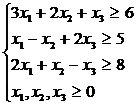
Rezolvare:
min f = 4 x1 + 5 x2 + 3 x3
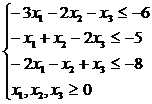
|
cB |
B |
4 |
5 |
3 |
0 |
0 |
0 |
c |
|
P1 |
P2 |
P3 |
P4 |
P5 |
P6 |
b |
||
|
0 0 0 |
P4 P5 P6 |
-3 -1 [-2] |
-2 1 -1 |
-1 -2 1 |
1 0 0 |
0 1 0 |
0 0 1 |
-6 -5 -8 |
|
fj cj - fj |
0 4 |
0 5 |
0 3 |
0 0 |
0 0 |
0 0 |
0 - |
|
|
0 5 0 |
P4 P5 P1 |
0 0 1 |
-1/ 2 3/2 1/ 2 |
-5/2 [-5/2] -1/ 2 |
1 0 0 |
0 1 0 |
-3/2 -1/2 -1/2 |
6 -1 4 |
|
fj cj - fj |
4 0 |
2 3 |
-2 5 |
0 0 |
0 0 |
-2 2 |
16 - |
|
|
0 3 4 |
P4 P3 P1 |
0 0 1 |
-2 -3/5 1/5 |
0 1 0 |
1 0 0 |
-1 -2/5 -1/5 |
-1 1/5 -2/5 |
7 2/5 21/5 |
|
fj cj - fj |
4 0 |
-1 6 |
3 0 |
0 0 |
-2 2 |
-1 1 |
18 - |
|
Solutia optima va fi x opt = (21/5, 0, 2/5, 7, 0, 0) t si f min = 18.
REOPTIMIZAREA PROBLEMELOR DE PROGRAMARE LINIARA
Modificarea vectorului c
(1)
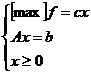 (2)
(2) 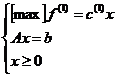
daca cj(1) - fj(1) 0 atunci solutia optima a problemei (1) este solutie
optima si pentru problema (2)
daca cj(1) - fj(1) > 0 atunci se trece la imbunatatirea solutiei .
Modificarea vectorului b
Pornind de la solutia optima a problemei (1) vrem sa determinam solutia optima a problemei
(3) 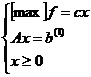
Se considera iteratia optima a problemei (1) in care se recalculeaza coloana termenilor liberi B -1 b (1):
daca B -1 b (1) 0 atunci solutia este optima;
daca exista elemente in aceasta coloana negative, atunci se continua cu
algoritmul simplex dual.
Modificarea unui vector coloana P j din matricea A
Pornind de la solutia optima a problemei (1) vrem sa determinam solutia optima a problemei .
(4) 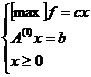
Se considera iteratia optima a problemei (1) in care se recalculeaza elementele coloanei P j astfel B -1 P j(1) .
- daca vectorul P j nu face parte din baza optima atunci se verifica conditia de optim doar pentru acest vector si se actioneaza in consecinta;
- daca vectorul P j face parte din baza optima atunci se trece la schimbarea bazei.
Adaugarea de noi coloane la matricea A
Pornind de la solutia optima a problemei (1) vrem sa determinam solutia optima a problemei:
(5) 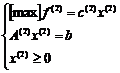
Pentru reoptimizare se procedeaza ca in precedentele cazuri utilizand B-1. Se vor calcula valorile din liniile f j si c j - f j corespunzatoare noii coloane si se va actiona in consecinta.
Modificarea unei linii a matricei restrictiilor
- Pornind de la solutia optima a problemei (1) vrem sa determinam solutia optima a problemei:
(6) 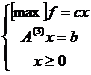
- Modificarea unei linii a matricei restrictiilor inseamna de fapt modificarea simultana a mai multor coloane ale acestei matrici si ca urmare sunt posibile cazurile:
1) linia modificata nu schimba elementele coloanelor bazice si atunci sunt afectate doar diferentele cj-fj ,
2) linia modificata schimba elemente ale coloanelor bazice si atunci sunt afectate atat diferentele cj-fj cat si solutia xB.
Observatie
Utilitatea practica a reoptimizarii se poate reflecta prin:
1) eficienta procedeului in raport cu solutionarea problemei modificate ca o problema noua, atunci cand se poate, deoarece calculele se reiau de la solutia optima a problemei date si se studiaza efectul modificarilor asupra optimalitatii solutiei;
2) posibilitatea simularii unor modificari pentru a cunoaste existenta sau inexistenta unor solutii optime sub influenta variatiilor elementelor definitorii ale modelului.
PROGRAMARE LINIARA PARAMETRICA
Consideram problema de programare liniara:
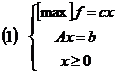
si vom analiza cazurile cand vectorii b si respectiv c depind liniar de un parametru.
Parametrizarea vectorului c
Fie problema de programare liniara parametrica
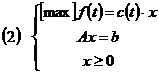
unde ![]() vectori
constanti.
vectori
constanti.
Pentru rezolvarea problemei (2) se parcurg etapele:
- pentru t = t0 (fixat) se rezolva problema cu algoritmul simplex;
- se reoptimizeaza problema de la 1) cu datele c(t);
- din conditiile de optim cj(t) - fj(t) 0 se deduce un subinterval [ ] in care solutia gasita este optima.
daca [α, β] = [a, b] atunci rezolvarea s-a incheiat.
daca
[α, β] ![]() [a, b] atunci se trece
la etapa urmatoare;
[a, b] atunci se trece
la etapa urmatoare;
- se ia 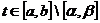 si se
continua cu reoptimizarea obtinand un nou subinterval [α1,
β1] etc. se continua astfel, pana cand reunirea
subintervalelor gasite coincide cu [a, b].
si se
continua cu reoptimizarea obtinand un nou subinterval [α1,
β1] etc. se continua astfel, pana cand reunirea
subintervalelor gasite coincide cu [a, b].
Observatie Conditiile de optim cj(t) - fj(t) 0 sunt cele care conduc la determinarea subintervalelor in care solutia este optima.
Parametrizarea vectorului b
In problema de programare liniara parametrica
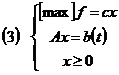
unde b(t) = b1 +tb2, t![]() [a, b], b1 +b2 vectori constanti
[a, b], b1 +b2 vectori constanti
Pentru rezolvarea problemei (3) se parcurg etapele:
- pentru t = t0 ![]() [a, b] se rezolva
problema in mod obisnuit;
[a, b] se rezolva
problema in mod obisnuit;
- se reoptimizeaza problema de la 1) cu datele d(t);
- din conditiile de admisibilitate B-1b(t)
0 se deduce un interval real [α,
β] in care solutia gasita este admisibila deci si
optima. Daca [α, β] = [a, b] rezolvarea s-a incheiat,
astfel ([α, β] ![]() [a, b]) se trece la etapa urmatoare.
[a, b]) se trece la etapa urmatoare.
- se ia t![]() [a, b][α, β] si se continua cu
reoptimizarea aplicand algoritmul simplex dual, pana cand reuniunea
subintervalelor gasite coincide cu [a, b].
[a, b][α, β] si se continua cu
reoptimizarea aplicand algoritmul simplex dual, pana cand reuniunea
subintervalelor gasite coincide cu [a, b].
Observatie Conditiile de admisibilitate B-1b(t) 0 sunt acelea care conduc la determinarea subintervalelor in care solutia este optima.
PROBLEME DE TRANSPORT
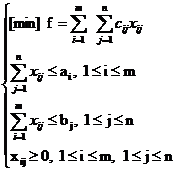
1. De obicei se urmareste satisfacerea totala atat a cererii cat si a disponibilului si prin urmare restrictiile problemei apar ca egalitati. Acestora li se pot adauga si alte restrictii cu semnificatii diverse.
2. Daca in locul unui anumit produs care sa poata fi efectiv transportat consideram ca a 1 - a m sunt suprafete cultivabile de o aceeasi calitate, iar B 1 . Bn sunt n culturi care au nevoie de un astfel de teren, atunci problema amplasarii optime a culturilor are modelul matematic anterior, dar nu este vorba de o operatiune de transport. Este unul din motivele pentru care spunem modele de tip transport.
Sa consideram un anumit fond banesc de valoare S unitati monetare (u.m) care trebuie repartizat sau alocat:
1. la un moment dat pentru n activitati sau
2. unei anumite activitati la n momente (adica esalonat).
Sa notam cu x j, j =![]() , partea din fond care se aloca pentru activitatea de ordin j (sau la momentul j) si cu cj, profitul unitar realizat pentru fiecare unitate monetara investita sau alocata. Atunci profitul total va fi: f = c1 x1 + c2
x2 + . + cn xn urmand a fi maximizat, ceea ce
conduce la problema:
, partea din fond care se aloca pentru activitatea de ordin j (sau la momentul j) si cu cj, profitul unitar realizat pentru fiecare unitate monetara investita sau alocata. Atunci profitul total va fi: f = c1 x1 + c2
x2 + . + cn xn urmand a fi maximizat, ceea ce
conduce la problema:
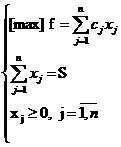
Este posibila adaugarea unor restrictii de forma a j x j b j j p n, in care x j a j > 0 ar insemna "un prag sau nivel minimal necesar util" sub care investitia nu prezinta interes, iar x j b j < S ar insemna "un nivel maximal posibil de credit garantat" care poate fi acoperit de catre debitor prin diverse garantii sau cu averea sa. In acest caz problema devine:
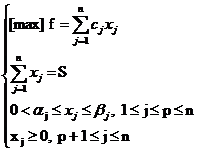
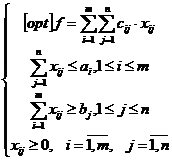
unde: -![]() reprezinta fie costul total al operatiunii de tip
transport (cand opt = min), fie profitul total al operatiunii de tip
transport (cand opt = max).
reprezinta fie costul total al operatiunii de tip
transport (cand opt = min), fie profitul total al operatiunii de tip
transport (cand opt = max).
ai reprezinta disponibilul furnizorului
Fi, ![]() ;
;
bj reprezinta necesarul beneficiarului Bj, ![]() ;
;
cij reprezinta costul unitar (sau
profitul unitar) pe relatia ![]() ;
;
xij reprezinta cantitatea
transportata (alocata, repartizata, transferata) de la
furnizorul Fi la
beneficiarul Bj, ![]()
![]() ;
;
restrictia ![]() arata ca nu
se poate aloca tuturor beneficiarilor mai mult decat este disponibil
furnizorului Fi;
arata ca nu
se poate aloca tuturor beneficiarilor mai mult decat este disponibil
furnizorului Fi;
restrictia ![]() arata ca de
la toti furnizorii se aloca pentru beneficiarul Bj cel putin cat este necesarul sau;
arata ca de
la toti furnizorii se aloca pentru beneficiarul Bj cel putin cat este necesarul sau;
![]() reprezinta
disponibilul (sau oferta) tuturor furnizorilor iar
reprezinta
disponibilul (sau oferta) tuturor furnizorilor iar ![]() reprezinta
necesarul (sau cererea) tuturor beneficiarilor in ipoteza ca
insumarile au sens (in caz contrar nu are sens problema).
reprezinta
necesarul (sau cererea) tuturor beneficiarilor in ipoteza ca
insumarile au sens (in caz contrar nu are sens problema).
Se spune ca o problema de tip transport este:
echilibrata daca oferta totala este egala cu cererea totala a = b
neechilibrata daca oferta totala difera de cererea totala (a ≠ b)
|
Fi |
B1 |
B2 |
Bn |
Disponibil |
|||||||||||||
|
F1 |
c11 x11 |
c12 x12 |
c1n x1n |
a1 |
|||||||||||||
|
F2 |
c21 x21 |
c22 x22 |
c2n x2n |
a2 |
|||||||||||||
|
Fm |
xm1 cm1 |
xm2 cm2 |
xmn cmn |
am |
|||||||||||||
|
Necesar |
b1 |
b2 |
bn |
b |
cij
1. Ansamblul poarta denumirea de casuta.
xij
2. Conceptul de echilibrare este fundamental pentru construirea procedurii de solutionare a unei probleme de tip transport.
3. Daca egalitatea intre disponibilul total si necesarul total nu are loc se poate trece la o problema echilibrata prin considerarea fie a unui furnizor fictiv, Fm+1, fie a unui beneficiar fictiv, Bn+1, care ofera sau solicita, diferenta dintre cele doua sume.
4. Intrucat algoritmul presupune un volum mare de calcule, pentru acest tip de problema de programare liniara se va prezenta un algoritm distributiv.
a) Metoda nord-vest consta in a atribui, pe rand, valori variabilelor incepand cu cea din coltul nord-vest a tabelului, apoi se continua la fel cu subtabelul ramas.
Astfel x11 = min (a1, b1), daca min (a1, b1) = a1 atunci x12 = =x1n = 0, daca min (a1, b1) = b1 atunci x21 = = xm1 = 0 si apoi vom continua cu x21 = min (a2, b1-a1) respectiv in cealalta situatie cu x12 = min (a1-b1, b2) etc.
Acest procedeu se repeta pana cand este atribuita si ultima valoare variabilelor.
Valoarea 0 este marcata in tabel printr-un punct.
|
|
|
|
|
40
|
|
|
25
[min]f = 4x11 + 2x12 + x13 + 2x21 + x22 + 3x23
f = 4 10 + 2 30 + 1 5 + 3 20 = 165.
b) Metoda elementului (costului ) minim consta in a atribui, pe rand, valori variabilelor incepand cu aceea pentru care costul unitar este minim. Apoi se continua cu variabila pentru care costul unitar este minim dintre cele ramase etc. Daca sunt mai multe costuri minime egale atunci se va considera mai intai acea variabila care poate lua valoare mai mare. Valoarea variabilei se determina ca si la metoda nord-vest, considerand minimul dintre disponibilul si necesarul corespunzator.
c) Metoda costului minim pe linie consta din a aloca pentru fiecare casuta (i, j) o cantitate xij egala cu minimul dintre cererea si oferta existenta in momentul acelei alocari, procedeul aplicandu-se pe fiecare linie in ordinea crescatoare a costurilor unitare cij. Algoritmul poate incepe cu oricare linie dar pentru organizarea calculelor acesta incepe cu prima linie si decurge ca si in cazul metodei coltului din nord-vest.
d) Metoda costului minim pe coloana este un procedeu analog cu precedentul cu singura deosebire ca se aplica pe fiecare coloana, preferabil incepand cu prima coloana.
|
|
x22 = min (25, 35) deci x21 = x23 = 0 apoi x13 = min (40, 20) = 20 iar x12 = min (20, 10) = 10 si x11 = 10. Avem f = 410 + 210 + 120 +125 = 105.
Fie problema de transport:
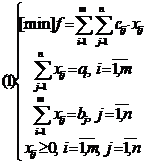
Scriem duala acesteia notand cu u1, u2, , um, v1, v2, , vn variabilele actuale.
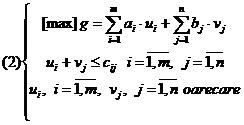
1)Din teorema
dualitatii avem ca ![]() este solutie
optima daca variabilele duale verifica restrictiile din
problema (2) adica:
este solutie
optima daca variabilele duale verifica restrictiile din
problema (2) adica:
(3) ui + vj
= cij daca ![]()
(4) ui + vj
cij daca ![]()
2) (3) si (4) sunt de fapt conditiile de optimizare pentru o solutie de baza x = (xij) a problemei de transport.
3) (3) este un sistem de m + n - 1 ecuatii cu m + n necunoscute. Pentru rezolvare se alege u1 = 0 si atunci rezolvarea se face direct pe tabelul de solutii, cand ui si vj se vor trece la marginea tabelului, de aceea se mai numesc si valori marginale.
Definitii
1) O solutie x = (xij) a problemei (1) se numeste nedegenerata daca are exact m + n - 1 valori nenule, in caz contrar ea va fi solutie degenerata.
2) Se numeste ciclu al unei casute o succesiune de casute doua cate doua alaturate in aceeasi linie, sau respectiv in aceeasi coloana.
3) Intr-un ciclu casutele impare sunt: prima (libera), a treia (ocupata), a cincea (ocupata) etc., iar casutele pare sunt a doua (ocupata), a patra (ocupata) etc.
4) Procedeul de imbunatatire a unei solutii consta in a trece de la o solutie la alta solutie mai buna. Aceasta se realizeaza prin modificarea valorilor variabilelor din casutele ce formeaza un ciclu dupa cum urmeaza:
se determina valoarea minima a valorilor variabilelor din casutele pare;
se aduna aceasta valoare minima la valorile variabilelor din casutele impare;
se scade aceasta valoare minima din valorile variabilelor din casutele pare.
ALGORITMUL DISTRIBUTIV
Etapele algoritmului distributiv pentru determinarea solutiei optime a problemei de transport (1) sunt:
- se determina o solutie initiala de baza;
- se calculeaza valorile variabilelor duale (valorile marginale) ui, vj ca solutii ale sistemului de ecuatii ui + vj = cij, unde indicii i, j sunt cei ai variabilelor bazice (casutele ocupate);
- se verifica optimalitatea solutiei de baza, adica se verifica inegalitatea ui + vj cij pentru toti indicii corespunzatori variabilelor nebazice (casute libere);
- daca solutia de baza nu este optima se imbunatateste solutia;
- se reiau etapele 2), 3), 4) cu noua solutie de baza si se continua pana cand toate conditiile de optimalitate sunt indeplinite;
- se scrie solutia optima si se calculeaza valoarea minima a functiei scop.
Exemplu Sa se rezolve problema de transport formulata in exemplul anterior
Rezolvare: Vom parcurge etapele algoritmului distributiv, direct pe tabel. Consideram solutia initiala obtinuta prin metoda nord-vest. Avem:
|
v1 = 4 |
v2 = 2 |
v3 = 4 | ||
|
u1 = 0 |
|
u2 = 1
Intrucat u1 + v3 = 4 > 1 = c13 si u2 + v1 = 3 > 2 = c21 solutia este optima.
Formand ciclul casutei (1,3) se trece la o solutie mai buna si marcam cu "+" casutele impare si cu "-" casutele pare. Se obtine solutia:
|
v1 = 4 |
v2 = 2 |
v3 = 1 | ||
|
u1 = 0 |
|
u2 = 1
Deoarece u2 + v1 = 3 > 2 = c21, solutia nu este optima si formam ciclul casutei (2, 1) pentru a obtine o solutie mai buna.
|
v1 = 3 |
v2 = 2 |
v3 = 1 |
|
|
u1 = 0 |
|
u2 = -1
Aceasta este solutia optima a problemei de transport:
![]() si fmin
= 2
si fmin
= 2
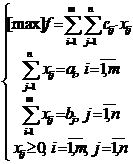
Pentru determinarea solutiilor de baza, metoda coltului din nord-vest ramane neschimbata iar metoda costului minim se inlocuieste cu metoda costului maxim. In ceea ce priveste determinarea solutiei optime pornind de la o solutie de baza nedegenerata, in cazul problemei de maximizare se verifica inegalitatea ui + vj cij pentru toti i si j.
Degenerarea apare, de obicei, in urmatoarele situatii:
la determinarea solutiei initiale de baza cand valoarea disponibilului este egala cu valoarea necesarului deci se "taie" atat linia cat si coloana corespunzatoare (exceptand ultima casuta ocupata);
in procesul de imbunatatire a solutiei cand valoarea minima din casutele pare este atinsa in doua sau mai multe casute.
In aceste situatii se obtin mai putine casute ocupate, deci variabilele duale nu pot fi determinate. Acest neajuns se inlatura prin considerarea unor casute libere ca fiind "ocupate"cu 0. Acest 0 se considera in casutele cu costuri minime, care nu formeaza cicluri cu casutele deja ocupate, astfel incat in final numarul casutelor ocupate este m + n - 1.
Cand degenerarea apare in a doua situatie, zerourile esentiale se inscriu in acel casute pare care devin libere si in care costurile sunt mai mici.
Solutii multiple Pot exista mai multe solutii atunci cand, desi solutia este optima, exista casute libere la care ui + vj = cij deci conditia de optim este verificata cu egalitate. Celelalte solutii optime, daca exista, se vor obtine urmand procedeul imbunatatirii solutiei cu casutele libere in care ui + vj = cij. Solutia generala va fi combinatia liniara convexa a solutiilor gasite.
REOPTIMIZAREA PROBLEMELOR DE TRANSPORT
Fie problema de transport:
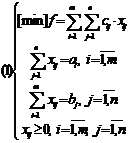
pe care o presupunem rezolvata cu algoritmul distributiv.
Reoptimizarea in cazul modificarii matricei costurilor
Plecand de la tabelul care
contine solutia optima a problemei (1) se verifica
optimalitatea acestei solutii folosind elementele ![]() :
:
daca
![]() atunci solutia
este optima si pentru problema modificata;
atunci solutia
este optima si pentru problema modificata;
daca cel putin o conditie de optim nu este indeplinita atunci se va trece la imbunatatirea solutiei.
Reoptimizarea problemelor de transport in cazul modificarii si/sau necesarului
Pornind de la tabelul care
contine solutia optima a problemei (1) cu noile
cantitati pentru disponibil si/sau necesar ![]() se vor ocupa exact
aceleasi casute, chiar cu riscul aparitiei, in unele
casute, a unei valori negative.
se vor ocupa exact
aceleasi casute, chiar cu riscul aparitiei, in unele
casute, a unei valori negative.
Daca toate casutele sunt ocupate cu valori nenegative atunci solutia ramane optima si pentru problema modificata.
Daca cel putin intr-o casuta apare o valoare negativa atunci cand se formeaza ciclul acestei casute, cu varf pozitiv in aceasta casuta se vor modifica valorile variabilelor din casutele acestui ciclu cu cantitatea egala cu valoarea negativa din casuta de pornire si apoi se procedeaza dupa caz.
Probleme de transport parametrice
Consideram problema de transport:
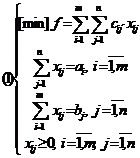
Presupunem ca problema
(1) este parametrica ![]() ,
, ![]() . Rezolvarea problemei se face in urmatoarele etape:
. Rezolvarea problemei se face in urmatoarele etape:
Pentru t = t0 ![]() [a, b] se rezolva
problema in mod obisnuit;
[a, b] se rezolva
problema in mod obisnuit;
Se reoptimizeaza problema cu valorile cij(t);
Din conditiile de optim ui(t) + vj(t) cij(t) se deduce un subinterval [ ] in care solutia gasita este optima. Daca [ ] = [a, b] atunci rezolvarea s-a incheiat, in caz contrar se continua cu etapa urmatoare.
Se ia t ![]() [a, b]- [ ] si se continua cu reoptimizarea pana cand reunirea
intervalelor gasite coincide cu [a, b].
[a, b]- [ ] si se continua cu reoptimizarea pana cand reunirea
intervalelor gasite coincide cu [a, b].
Parametrizarea disponibilului si/sau necesarului
Consideram problema (1)
in care ![]() si/sau
si/sau ![]() , t
, t![]() [a, b]. Rezolvarea problemei se face in urmatoarele
etape:
[a, b]. Rezolvarea problemei se face in urmatoarele
etape:
pentru t = t0![]() [a, b] se rezolva problema in mod obisnuit;
[a, b] se rezolva problema in mod obisnuit;
se reoptimizeaza problema cu noile valori ai(t), bj(t), decupand exact aceleasi casute ca la punctul 1);
din conditiile de admisibilitate (valorile variabilelor din casutele ocupate sa fie nenegative) se deduce un subinterval [ ] in care solutia este optima. Daca [ ] = [a, b] atunci rezolvarea s-a incheiat, in caz contrar se continua cu etapa urmatoare;
se ia t ![]() [a, b] - [ ] si se continua cu reoptimizarea din cazul cand solutia nu
este admisibila, pana ce reuniunea subintervalelor gasite
coincide cu [a, b].
[a, b] - [ ] si se continua cu reoptimizarea din cazul cand solutia nu
este admisibila, pana ce reuniunea subintervalelor gasite
coincide cu [a, b].
PROBLEME DE TIP TRANSPORT SPECIALE
Exista anumite probleme practice care se aseamana cu modele liniare de tip transport dar care au anumite particularitati sau conditii speciale care se adauga celor care definesc modelul initial. Prin anumite transformari ele sunt aduse la forma unui model de tip transport si se rezolva cu algoritmul distributiv, dupa care se revine la problema initiala.
Presupunem ca furnizorii F1 Fp, p < m au oferta comuna. Vom nota cu FG furnizorul grupat. Aducerea problemei la forma obisnuita inseamna "personalizarea furnizorului comun" si acest lucru poate fi realizat prin:
1) identificarea furnizorului grupat cu unul dintre furnizori ceea ce poate conduce de fapt la p probleme obisnuite;
2) definirea costurilor (sau
beneficiarilor) furnizorului grupat prin ![]() in cazul problemelor
de minimizare sau prin
in cazul problemelor
de minimizare sau prin ![]() in cazul problemelor
de maximizare.
in cazul problemelor
de maximizare.
In mod analog, daca avem cererea grupata B1 Bq, q < n, putem introduce beneficiarul grupat BG a carui personalizare se poate face prin:
1) identificarea beneficiarului grupat cu unul dintre beneficiari, fiind condusi la q probleme obisnuite;
2) definirea costurilor (sau beneficiilor) beneficiarului grupat prin:
![]() pentru probleme de
minimizare sau prin :
pentru probleme de
minimizare sau prin :
![]() pentru probleme de
maximizare.
pentru probleme de
maximizare.
Daca problema are atat furnizor grupat cat si beneficiar atunci se poate proceda ca mai sus, secvential; determinand mai intai furnizorul comun
si apoi beneficiarul comun sau invers.
Presupunem ca relatia sau legatura Fi0 Bj0 este incompatibila, atunci in tabelul problemei de transport se hasureaza casuta (i0, j0) pentru a fi evitata in calcule, dupa care se rezolva problema in mod obisnuit.
Problema impune alocare obligatorie a cantitatii xi0j0 = d pe relatia (Fi0, Bj0), 1 i0 m, 1 j0 n. Ca urmare problema initiala se modifica la nivelul furnizorului Fi0 care va dispune de cantitatea (ai0 - d) si la nivelul beneficiarului Bj0 care va solicita (bj0 - d). Relatia impusa (Fi0, Bj0) va ramane acum ca o legatura interzisa si se rezolva problema.
|
Banci |
A1 |
A2 |
A3 |
A4 |
Disponibil bancar |
|
B1 |
|
B2
B3
Necesar
anual
Rezolvare:
Deoarece x14 = 20 u.m. si x32 = 40 u.m. problema modificata (ca si cum ar avea legaturi interzise) este data de tabelul:
|
Banci |
A1 |
A2 |
A3 |
A4 |
Disponibil bancar |
|
B1 |
|
 4
4
20
B2
B3
 5
5
40
Necesar
anual
Aplicam metoda costului minim pe linie si obtinem solutia optima care evident ca nu mai este solutie de baza si anume:
|
v1 = -2 |
v2 =1 |
v3 = 1 |
v4 = 0 | ||
|
u1 = 0 |
 4
4
20
80
u2 = 1
u3= 3
 5
5
40
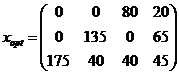 , fmin =
885.
, fmin =
885.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 7423
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved