Metode de rezolvare a algoritmilor euristici

Metode de rezolvare a algoritmilor euristici

1. Metoda greedy

Algoritmii greedy (greedy = lacom) sunt in general simpli si sunt folositi la probleme de optimizare, cum ar fi: sa se gaseasca cea mai buna ordine de executare a unor lucrari pe calculator, sa se gaseasca cel mai scurt drum intr-un graf etc. In cele mai multe situatii de acest fel avem:

o multime de candidati (lucrari de executat, varfuri ale grafului etc)

o functie care verifica daca o anumita multime de candidati constituie o solutie posibila, nu neaparat optima, a problemei

o functie care verifica daca o multime de candidati este fezabila, adica daca este posibil sa completam aceasta multime astfel incat sa obtinem o solutie posibila, nu neaparat optima, a problemei

o functie de selectie care indica la orice moment care este cel mai promitator dintre candidatii inca nefolositi

o functie obiectiv care da valoarea unei solutii (timpul necesar executarii tuturor lucrarilor intr-o anumita ordine, lungimea drumului pe care l-am gasit etc); aceasta este functia pe care urmarim sa o optimizam (minimizam/maximizam)

Pentru a rezolva problema noastra de optimizare, cautam o solutie posibila care sa optimizeze valoarea functiei obiectiv. Un algoritm greedy construieste solutia pas cu pas. Initial, multimea candidatilor selectati este vida. La fiecare pas, incercam sa adaugam acestei multimi cel mai promitator candidat, conform functiei de selectie. Daca, dupa o astfel de adaugare, multimea de candidati selectati nu mai este fezabila, eliminam ultimul candidat adaugat; acesta nu va mai fi niciodata considerat. Daca, dupa adaugare, multimea de candidati selectati este fezabila, ultimul candidat adaugat va ramane de acum incolo in ea. De fiecare data cand largim multimea candidatilor selectati, verificam daca aceasta multime nu constituie o solutie posibila a problemei noastre. Daca algoritmul greedy functioneaza corect, prima solutie gasita va fi totodata o solutie optima a problemei. Solutia optima nu este in mod necesar unica: se poate ca functia obiectiv sa aiba aceeasi valoare optima pentru mai multe solutii posibile.

Descrierea formala a unui algoritm greedy general este:

function greedy(C)

S
while not solutie(S) and C do
x un element din C care maximizeaza/minimizeaza select(x)
C C if fezabil(S ) then S S
if solutie(S) then return S
else return "nu exista solutie"

Este de inteles acum de ce un astfel de algoritm se numeste "lacom" (am putea sa-i spunem si "nechibzuit"). La fiecare pas, procedura alege cel mai bun candidat la momentul respectiv, fara sa-i pese de viitor si fara sa se razgandeasca. Daca un candidat este inclus in solutie, el ramane acolo; daca un candidat este exclus din solutie, el nu va mai fi niciodata reconsiderat. Asemenea unui intreprinzator rudimentar care urmareste castigul imediat in dauna celui de perspectiva, un algoritm greedy actioneaza simplist.

Totusi, ca si in afaceri, o astfel de metoda poate da rezultate foarte bune tocmai datorita simplitatii ei.

Functia select este de obicei derivata din functia obiectiv; uneori aceste doua functii sunt chiar identice.

Un exemplu simplu de algoritm greedy este algoritmul folosit pentru rezolvarea urmatoarei probleme: sa presupunem ca dorim sa dam restul unui client, folosind un numar cat mai mic de monezi. In acest caz, elementele problemei sunt:

candidatii: multimea initiala de monezi de 1, 5, si 25 unitati, in care presupunem ca din fiecare tip de moneda avem o cantitate nelimitata

o solutie posibila: valoarea totala a unei astfel de multimi de monezi selectate trebuie sa fie exact valoarea pe care trebuie sa o dam ca rest

o multime fezabila: valoarea totala a unei astfel de multimi de monezi selectate nu este mai mare decat valoarea pe care trebuie sa o dam ca rest

functia de selectie: se alege cea mai mare moneda din multimea de candidati ramasa

functia obiectiv: numarul de monezi folosite in solutie; se doreste minimizarea acestui numar

Se poate demonstra ca algoritmul greedy va gasi in acest caz mereu solutia optima (restul cu un numar minim de monezi). Pe de alta parte, presupunand ca exista si monezi de 12 unitati sau ca unele din tipurile de monezi lipsesc din multimea initiala de candidati, se pot gasi contraexemple pentru care algoritmul nu gaseste solutia optima, sau nu gaseste nici o solutie cu toate ca exista solutie.

Evident, solutia optima se poate gasi incercand toate combinarile posibile de monezi. Acest mod de lucru necesita insa foarte mult timp.

Un algoritm greedy nu duce deci intotdeauna la solutia optima, sau la o solutie. Este doar un principiu general, urmand ca pentru fiecare caz in parte sa determinam daca obtinem sau nu solutia optima

Pentru anumite probleme, se poate accepta utilizarea unor algoritmi despre care nu se stie daca furnizeaza solutia optima, dar care furnizeaza rezultate "acceptabile", sunt mai usor de implementat si mai eficienti decat algoritmii care dau solutia optima. Un astfel de algoritm se numeste euristic.

Una din ideile frecvent utilizate in elaborarea algoritmilor euristici consta in descompunerea procesului de cautare a solutiei optime in mai multe subprocese succesive, fiecare din aceste subprocese constand dintr-o optimizare. O astfel de strategie nu poate conduce intotdeauna la o solutie optima, deoarece alegerea unei solutii optime la o anumita etapa poate impiedica atingerea in final a unei solutii optime a intregii probleme; cu alte cuvinte, optimizarea locala nu implica in general, optimizarea globala. Regasim, de fapt, principiul care sta la baza metodei greedy. Un algoritm greedy, despre care nu se poate demonstra ca furnizeaza solutia optima, este un algoritm euristic.

Vom da doua exemple de utilizare a algoritmilor greedy euristici.

Probleme rezolvate:

1. Colorarea unui graf

Fie G = <V, M> un graf neorientat, ale carui varfuri trebuie colorate astfel incat oricare doua varfuri adiacente sa fie colorate diferit. Problema este de a obtine o colorare cu un numar minim de culori.

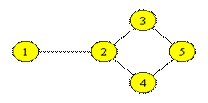Folosim urmatorul algoritm greedy: alegem o culoare si un varf arbitrar de pornire, apoi consideram varfurile ramase, incercand sa le coloram, fara a schimba culoarea. Cand nici un varf nu mai poate fi colorat, schimbam culoarea si varful de start, repetand procedeul.

Figura 6.

Daca in graful din Figura 6 pornim cu varful 1 si il coloram in rosu, mai putem colora tot in rosu varfurile 3 si 4. Apoi, schimbam culoarea si pornim cu varful 2, colorandu-l in albastru. Mai putem colora cu albastru si varful 5. Deci, ne-au fost suficiente doua culori. Daca coloram varfurile in ordinea 1, 5, 2, 3, 4, atunci se obtine o colorare cu trei culori.

Rezulta ca, prin metoda greedy, nu obtinem decat o solutie euristica, care nu este in mod necesar solutia optima a problemei. De ce suntem atunci interesati intr-o astfel de rezolvare? Toti algoritmii cunoscuti, care rezolva optim aceasta problema, sunt exponentiali, deci, practic, nu pot fi folositi pentru cazuri mari. Algoritmul greedy euristic propus furnizeaza doar o solutie "acceptabila", dar este simplu si eficient.

Un caz particular al problemei colorarii unui graf corespunde celebrei probleme a colorarii hartilor: o harta oarecare trebuie colorata cu un numar minim de culori, astfel incat doua tari cu frontiera comuna sa fie colorate diferit. Daca fiecarui varf ii corespunde o tara, iar doua varfuri adiacente reprezinta tari cu frontiera comuna, atunci hartii ii corespunde un graf planar, adica un graf care poate fi desenat in plan fara ca doua muchii sa se intersecteze. Celebritatea problemei consta in faptul ca in toate exemplele intalnite, colorarea s-a putut face cu cel mult 4 culori. Aceasta in timp ce, teoretic, se putea demonstra ca pentru o harta oarecare este nevoie de cel mult 5 culori. Recent s-a demonstrat pe calculator faptul ca orice harta poate fi colorata cu cel mult 4 culori. Este prima demonstrare pe calculator a unei teoreme importante.

Problema colorarii unui graf poate fi interpretata si in contextul planificarii unor activitati. De exemplu, sa presupunem ca dorim sa executam simultan o multime de activitati, in cadrul unor sali de clasa In acest caz, varfurile grafului reprezinta activitati, iar muchiile unesc activitatile incompatibile. Numarul minim de culori necesare pentru a colora graful corespunde numarului minim de sali necesare.

2. Problema comis - voiajorului

Se cunosc distantele dintre mai multe orase. Un comis-voiajor pleaca dintr-un oras si doreste sa se intoarca in acelasi oras, dupa ce a vizitat fiecare din celelalte orase exact o data. Problema este de a minimiza lungimea drumului parcurs. Si pentru aceasta problema, toti algoritmii care gasesc solutia optima sunt exponentiali.

Problema poate fi reprezentata printr-un graf neorientat, in care oricare doua varfuri diferite ale grafului sunt unite intre ele printr-o muchie, de lungime nenegativa. Cautam un ciclu de lungime minima, care sa se inchida in varful initial si care sa treaca prin toate varfurile grafului.

Conform strategiei greedy, vom construi ciclul pas cu pas, adaugand la fiecare iteratie cea mai scurta muchie disponibila cu urmatoarele proprietati:

nu formeaza un ciclu cu muchiile deja selectate (exceptand pentru ultima muchie aleasa care completeaza ciclul)

nu exista inca doua muchii deja selectate, astfel incat cele trei muchii sa fie incidente in acelasi varf

De exemplu, pentru sase orase a caror matrice a distantelor este data in tabel muchiile se aleg in ordinea: , , , , , si se obtine ciclul (1, 2, 3, 5, 4, 6, 1) de lungime 58. Algoritmul greedy nu a gasit ciclul optim, deoarece ciclul (1, 2, 3, 6, 4, 5, 1) are lungimea 56.

#include <stdio.h>

#include <conio.h>

#define nmax 10

/*Problema comis_voiajorului */

void comis_voiajor(int n,int c[nmax][nmax], int i,int ciclu[nmax+1],int cost)

/* n este nr.nodurilor; c este matricea costurilor;

i este nodul de start; ciclu contine nodurile din ciclu;

cost este costul ciclului */

*cost=*cost+costmin;

ciclu[k+1]=vmin;

p[vmin]=1;

v=vmin;

}

ciclu[n+1]=i;

*cost=*cost+c[v][i];

void main(void)

else break;

}

}

i=1;

comis_voiajor(n,c,i,ciclu,&cost_ciclu);

printf('nCOSTUL CICLULUI =%dn',cost_ciclu);

printf('nCICLUL=');

for(i=1;i<=n+1;i++)

printf('%3d',ciclu[i]);

getch();

2. Metoda Backtracking

Metoda Backtracking se utilizeaza la problemele in care solutia se poate reprezenta sub forma unui vector

x = (x₁ , x₂ , . , x_n) є S₁ x S₂ x . x S_n ,

unde multimile S₁ , S₂ , . , S_n sunt multimi finite avand s₁ , s₂ , . , s_n elemente ( unde am notat cu s_i cardinalul multimii S_i, i:=1, . ,n ).

Pentru fiecare problema concreta sunt date anumite relatii intre componenetele x₁ , x₂ , . , x_n ale vectorului x numite conditii interne.

Multimea finita S₁ x S₂ x . x S_n (pe care o sa o notam cu S) se numeste spatiul solutiilor posibile

Solutiile posibile care satisfac conditiile interne se numesc solutii rezultat

Ceea ce ne propunem este sa determinam toate solutiile rezultat (cu scopul de a le lista sau de a alege dintre ele una care maximizeaza sau minimizeaza o eventuala functie obiectiv data

Intrucat metoda de a determina solutiile rezultat prin generarea intr-un mod oarecare a tuturor solutiilor posibile si de a verifica daca ele satifac conditiile interne este costisitoare din punct de vedere al timpului de executie (determinarea tuturor solutiilor posibile dureaza foarte mult) si, prin urmare, nu este utila, vom utiliza o alta metoda, mult mai eficienta, cunoscuta sub numele de metoda Backtracking.

Metoda Backtracking urmareste sa evite generarea tuturor solutiilor posibile. In acest scop elementele vectorului x = ( x₁ , x₂ , . , x_n) primesc pe rand valori in ordinea crescatoare a indicilor, in sensul ca lui x_k i se atribuie o valoare numai daca au fost atribuite deja valori lui x₁ , x₂ , . , x_k-1. Mai mult, odata stabilita valoarea lui x_k-1, nu se trece direct la atribuirea de valori lui x_k , ci se verifica niste conditii de continuare referitoare la x₁ , x₂ , . , x_k-1. Aceste conditii stabilesc situatiile in care are sens sa trecem la calculul lui x_k , neindeplinirea lor exprimand faptul ca oricum am alege x_k , . , x_n nu vom putea ajunge la o solutie rezultat, adica o solutie pentru care conditiile interne sa fie satisfacute (deci conditiile de continuare sunt strict necesare pentru obtinerea unei solutii).

Evident in cazul neindeplinirii conditiilor de continuare va trebui sa facem inca o alegere pentru x_k sau, daca S_k a fost epuizata, se incearca sa se faca o noua alegere pentru componenta precedenta X_k-1 a vectorului (ceea ce inseamna sa micsoram pe k cu o unitate) dupa care facem o noua alegere pentru x_k. Aceasta revenire prin micsorarea lui k da numele metodei ilustrand faptul ca atunci cand nu putem avansa, urmarim inapoi secventa curenta din solutie. Este evident ca intre conditiile de continuare si conditiile interne exista o stransa legatura. O buna alegere pentru conditiile de continuare are ca efect o reducere a numarului de calcule.

Faptul ca valorile curente v₁ , v₂ , . , v_k-1 ale lui x₁ , x₂ , . , x_k-1 satisfac conditiile de continuare nu este suficient pentru a garanta ca se va obtine o solutie ale carei prime k-1 componente coincid cu valorile v₁ , v₂ , . , v_{k-1 .} De obicei conditiile de continuare reprezinta restrictia conditiilor interne la primele k componenet ale vectorului. Este evident ca in cazul k=n conditiile de continuare sunt chiar conditiile interne.

Prin metoda Backtracking, orice vector solutie este construit progresiv, incepand cu prima componenta si mergand catre ultima, cu eventuale reveniri asupra valorilor atribuite anterior (cu unul sau mai multi pasi inapoi, atat timp cat revenirea este posibila). Prin atribuiri sau incercari de atribuire esuate din cauza nerespectarii conditiilor de continuare, anumite valori sunt "consumate". O buna alegere pentru conditiile de continuare are ca efect o importanta reducere a numarului de calcule (cum vom vedea in exemplele care urmeaza

Prezentarea metodei sub forma de algoritm :

void main()

while(!( (!as) || (as&&ev)) );
if(as)

}
else k--;
}
}

Probleme rezolvate :

1. Problema     dispunerii reginelor:

Se da o tabla de sah de NxN casute. Sa se dispuna N regine astfel incat ele sa nu se atace.

Exemplu: Presupunand ca dispunem de o tabla de dimensiune 4 4, o solutie ar fi urmatoarea:

Cum procedam? Observam ca o dama trebuie sa fie plasata singura pe linie. Plasam prima dama pe linia 1 coloana 1.

A doua dama nu poate fi asezata decat pe coloana a 3-a.

Observam ca a treia dama nu poate fi plasata in linia a 3-a. Incercam atunci plasarea celei de-a doua dame in coloana a 4-a.

A treia dama nu poate fi plasata decat pe coloana a 2-a.

In aceasta situatie dama a patra nu mai poate fi asezata. Incercand sa avansam cu dama a treia, observam ca nu este posibil sa o plasam nici in coloana a treia, nici in coloana a patra, deci o vom scoate de pe tabla. Dama a doua nu mai poate avansa, deci si ea este scoasa de pe tabla. Avansam cu prima dama in coloana a doua.

A doua dama nu poate fi asezata decat in coloana a patra.

Dama a treia se aseaza in prima coloana.

Acum este posibil sa plasam a patra dama in coloana a treia si astfel am obtinut o solutie a problemei.

Algoritmul continua in acest mod pana cand trebuie scoasa de pe tabla prima dama.

Pentru prezentarea unei solutii putem folosi un vector cu n componente (avand in vedere ca pe fiecare linie se gaseste o singura dama). Exemplu: pentru solutia gasita avem vectorul st ce poate fi asimilat unei stive.

Doua dame se gasesc pe aceeasi diagonala daca si numai daca este indeplinita conditia. |st (i) - st (j)| = |i-j| : (diferenta, in modul, intre linii si coloane este aceeasi).

Exemplu: In tabla 4 4 avem situatia:

Sau situatia:

Intrucat doua dame nu se pot gasi pe aceeasi coloana, rezulta ca o solutie este sub forma de permutare. O prima idee ne conduce la generarea tuturor permutarilor si la extragerea solutiilor pentru problema (ca doua dame sa nu fie plasate in aceeasi diagonala). A proceda astfel, inseamna sa lucra conform strategiei backtracking. Aceasta presupune ca imediat ce am gasit doua dame care se ataca, sa reluam cautarea. Fata de programul de generare a tuturor solutiilor problemei celor n dame, are o singura conditie suplimentara, in procedura valid.

#include<fstream.h>
#include<conio.h>
#include<math.h>
ofstream g('dame.out');
int st[100],n,k,as,ev;
int pi,pd;
void init(int k, int st[])


void succesor(int& as, int st[], int k)

else as=0;
}


void valid(int& ev,int st[], int k)

}
int solutie(int k)

void tipar(int st[])

g<<endl;

}
cout<<endl;
}
void main()

while(!( (!as) || (as&&ev)) );
if(as)

}
else k--;
}}

2.Colorarea hartilor

Data fiind o harta, trebuie colorata fiecare tara cu o culoare astfel incat doua tari vecine sa fie colorate diferit. Orice harta poate fi colorata cu doar 4 culori.

Pentru exemplificare, vom considera urmatoarea harta unde tarile sunt numerotate cu cifre cuprinse intre 1 si 5:

O solutie a acestei probleme este urmatoarea:

tara 1 - culoarea 1

tara 2 - culoarea 2

tara 3 - culoarea 1

tara 4 - culoarea 3     Figura 7.

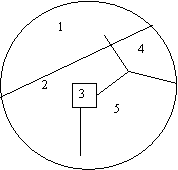
tara 5 - culoarea 4

Harta este furnizata programului

cu ajutorul unei matrice A_n,n

1, daca tara i

A(i,j) = se invecineaza cu tara j;

altfel

Matricea A este simetrica. Pentru rezolvarea

problemei se utilizeaza stiva st, unde nivelul

k al stivei simbolizeaza tara k, iar st[k] culoarea atasata tarii k. Stiva are inaltimea n si pe fiecare nivel ia valori intre 1 si 4.

#include<iostream.h>

#include<conio.h>
int st[100],n,k,as,ev,contor;

void init(int k, int st[])


void succesor(int& as, int st[], int k)

else as=0;
}

void valid(int& ev,int st[], int k)


int solutie(int k)

void tipar(int st[])

void main()

while(!( (!as) || (as&&ev)) );
if(as)

}
else k--;
}
cout<<contor;
}

Metoda divide et impera

Divide et impera este o tehnica speciala prin care se pot rezolva anumite probleme si se bazeaza pe un principiu extrem de simplu: se descompune problema in doua sau mai multe subprobleme (mai usoare), care se rezolva, iar solutia pentru problema initiala se obtine combinand solutiile problemelor in care a fost descompusa. Se presupune ca fiecare din probleme in care a fost descompusa problema initiala se poate descompune in alte subprobleme, la fel cum a fost descompusa problema initiala. Procedeul se reia pana cand (in urma descompunerilor repetate) se ajunge la probleme care admit rezolvare imediata

Evident nu toate problemele pot fi rezolvate prin utilizarea acestei tehnici. Fara teama de a gresi, putem afirma ca numarul lor este relativ mic, tocmai datorita cerintei ca problema sa admita o descompunere repetata

Divide et impera este o tehnica ce admite o implementare recursiva. Am invatat principiul general prin care se elaboreaza algoritmi recursivi: ce se intampla la un nivel, se intampla la orice nivel (avand grija sa asiguram conditiile de terminare). Tot asa, se elaboreaza un algoritm prin divide et impera: la un anumit nivel avem doua posibilitati:

am ajuns la o problema care admite o rezolvare imediata, caz in care se rezolva si se revine din apel(conditia de terminare);

nu am ajuns in situatia de la punctul 1, caz in care descompunem problema in doua sau mai multe subprobleme, pentru fiecare din ele reapelam functia, combinam rezultatele si revnim din apel.

Prezentarea metodei sub forma de algoritm:

function divimp(x)
    
     if x este suficient de mic then return prelucrez(x)
    
     for i := 1 to k do y_i := divimp(x_i)
    
      return y

Probleme rezolvate:

Se dau trei tije (STANGA MIJLOC DREAPTA) si n discuri de diferite dimensiuni, stivuite pe tija STANGA in ordine descrescatoare a dimensiunilor lor, formand un <turn> ca in figura (turnurile din Hanoi).

Fig.8.

Sa se scrie programul care muta cele n discuri de pe tija STANGA pe tija DREAPTA, astfel incat ele sa fie ordonate ca la inceput.

Mutarile se fac cu urmatoarele restrictii:

• la fiecare miscare se muta doar un disc;
• un disc nu poate fi plasat peste unul mai mic;
• tija MIJLOC poate fi utilizata ca pozitie intermediara

#include<iostream.h>
#include<conio.h>
int n;
void citire()

void muta(int a, int b)

void hanoi(int n,int a, int b, int c)

else

}
void main()

2. Se da un sir de N numere intregi si un intreg x. Sa se determine daca intregul x se afla in sir si daca da pe ce pozitie

#include<fstream.h>
#include<conio.h>
ifstream f('nr_max_d.in');
int i, a[100], j, n, x, poz, gasit, mij;
void citire(int v[])



void divide(int x,int i,int j,int v[])

if(j!=i && j-i!=1 && gasit==0)

}
void main()

Se da un vector cu n componente se cere sa se ordoneze vectorul crescator ( Quick Sort ).

#include<fstream.h>
ifstream f('quick.in');
ofstream g('quick.out');
int x[100],i,n;
void citire()

void afisare()

void quick(int s,int d)

}
while(b>a);
if(s<a-ia) quick(s,a-ia);
if(a-ia+1<d) quick(a-ia+1,d);
}

void main()

4.Metoda programarii dinamice

Este o metoda care se aplica problemelor in care rezultatul se obtine ca urmare a unei decizii D1, D2,., Dn. In urma deciziei D1 sistemul evolueaza din starea S0 in starea S1, in urma deciziei D2 sistemul evolueaza din starea S1 in starea S2,., in urma deciziei Dn, sistemul evolueaza din starea Sn-1 in starea Sn. In afara conditiilor satisfacute pana acum este necesar sa fie satisfacut principiul programarii dinamice, adica

Daca D1, D2, . , Dn este un sir de decizii care transforma sistemul din satrea initiala S0 in starea finala Sn, atunci trebuie indeplinita una dintre conditiile urmatoare:

Dk,.,Dn este un sir optim de decizii care transforma sistemul din starea Sk-1 in starea Sn, oricare ar fi k, 1<=k<=n;

D1,.,Dk este un sir optim de decizii care transforma sistemul din starea S0 in starea Sk, oricare ar fi k, 1<=k<=n;

Dk+1, . , Dn si D1, D2, . , Dk sunt siruri de decizii optime ce duc sistemul din starea Sk in starea Sn, respective din starea S0 in Starea Sk, oricare ar fi k, 1<=k<=n;

In cazul 1 fiecare decizie Dk depinde de deciziile Dk+1,., Dn si spunem ca se aplica metoda inainte.

In cazul 2 fiecare decizie Dk depinde de deciziile D1, ., Dk-1 si spunem ca se aplica metoda inapoi.

In cazul 3 spunem ca se aplica metoda mixta

Pentru a rezolva o problema utilizand programarea dinamica se procedeaza astfel:

se verifica principiul de optimalitate conform uneia dintre cele trei metode

se scriu relatiile ce apar, corespunzator metodei alese.

Probleme rezolvate:

Se da un vector cu N elemente numere intregi. Sa se tipareasca cel mai lung subsir crescator al vectorului.

#include<fstream.h>
#include<conio.h>
ifstream f('subsir.in');
int n,i,v[100],pred[100],a[100],imax,j;
void citire()

void afis(int i)

void main()

if(v[i]>v[imax]) imax=i;
}
afis(imax);
cout<<endl<<v[imax];
}