Analiza statistica a datelor in raport cu o variabila utilizand inferenta statistica

Analiza statistica a datelor in raport cu o variabila utilizand inferenta statistica

1. Elaborarea intervalului de incredere a valorii medii

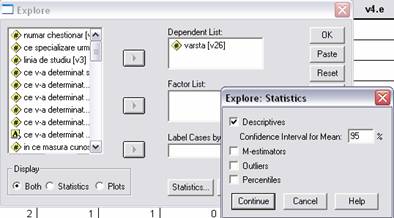
1.1. Elaborarea intervalului de incredere a valorii medii in ipoteza organizarii unui sondaj aleator simplu cu ajutorul comenzii Analyze - Descriptive Statistics - Explore introducem variabila studiata, avand posibilitatea de a fixa nivelul de incredere dorit (95%).

Limita inferioara a intervalului

Limita superioara a intervalului

Interpretare: Putem afirma cu o probabilitate de 95% ca varsta medie la nivelul populatiei cercetate este intre 21,88 si 22,14 ani. Sau, daca am efectua studiul de 100 de ori ( 100 esantioane ), in 95 de esantioane media va apartine intervalului, si numai in 5 esantioane valoarea acesteia ar depasi limitele intervalului.

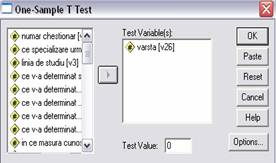
Acelasi rezultat se obtine si activand meniul Analyze - Compare Means - One Sample T Test;

1.2. Elaborarea intervalului de incredere a valorii medii in ipoteza organizarii unui sondaj aleator stratificat in meniul Analyze - Compare Means - One-way Anova introducem variabila cantitativa "varsta", dependenta de variabila factor de grupare "specializarea".

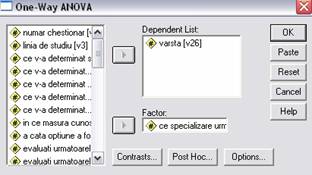In Options se bifeaza optiunea Descriptives.

Se obtin intervale de incredere pentru valorile medii de la nivelul fiecarei grupe.

2. Teste de semnificatie

2.1. Testarea semnificatiei unei medii face parte din grupa testelor parametrice. Folosind sirul de comenzi Analyze - Compare Means - One Sample T Test introducem variabila "varsta" pentru care avem valoarea medie observata egala cu 22,01 ani; dorim sa verificam daca varsta persoanelor din esantionul observat difera semnificativ de valoarea 25 de ani ( test value=25). Formulam ipoteza nula:

H: = 25 (varsta medie nu difera semnificativ de valoarea de 25 de ani)

H: ≠ 25

Interpretare: valoarea nivelului de semnificatie Sig = 0,000 <0,05 ( confidence interval ), ceea ce duce la respingerea ipotezei nule. Exista o diferenta semnificativa intre valoarea medie din esantion si cea specificata. Pentru ca Sig < 0,01 putem afirma ca intre valoarea medie de la nivel de esantion si cea specificata exista diferente semnificative la un nivel de incredere de 99%.

2.2. Testarea semnificatiei unei proportii din meniul Analyze - Nonparametric Tests - Binomial testam ipoteze cu privire la o variabila cu distributie binomiala, care poate lua doar doua valori, de exemplu anul de studiu ( anul 4 sau anul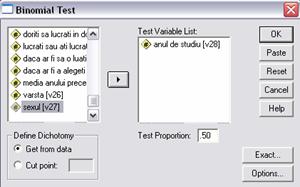

Dorim sa verificam daca proportia uneia dintre cele doua grupe de studenti definite prin variabila anul de "studiu" difera semnificativ de 0,50. Astfel formulam ipotezele : H: p = 50%

H: p ≠ 50%

Interpretare: proportia observata in esantion pentru grupa 1 ( anul 4 ) este de 90%, proportia specificata fiind de 50%. Valoarea Sig <0,01, astfel ca putem concluziona, cu o incredere de 99%, ca proportia studentilor din anul 4 difera semnificativ de proportia specificata.

3. Teste de concordanta - fac parte din categoria testelor neparametrice.

3.1.Verificarea normalitatii unei distributii modelarea statistica cere verificarea ipotezei de normalitate a variabilelor. Astfel, este foarte important ca inaintea inferentei statistice sa se verifice normalitatea distributiei populatiei. Pe langa vizualizarea histogramei si a valorilor coeficientilor de asimetrie si boltire, in SPSS exista posibilitatea aplicarii testului Kolmogorov - Smirnov, astfel: Analyze - Nonparametric Test - One Sample Kolmogorov-Smirnov Test:

Formulam ipoteza nula H: intre cele 2 distributii, cea teoretica si cea empirica nu exista diferente semnificative ( populatia este normal distribuita in raport cu variabila "varsta "), cu alternativa ca variabila nu urmeaza o lege normala.

Interpretare: nivelul gradului de semnificatie, Sig < 0,05 conduce la respingerea ipotezei nule, distributia studiata difera semnificativ de forma distributiei normale.

3.2. Verificarea uniformitatii unei distributii - se utilizeaza testul neparametric χ, care presupune urmatorul demers: Analyze - Nonparametric Tests - Chi Square Test.

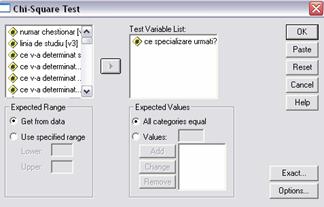
Formulam ipotezele referitoare la variabila specializarea

H: distributia este uniforma

H: distributia nu este uniforma

In tabelul urmator sunt comparate frecventele observate cu frecventele teoretice, pe coloana Residual fiind prezentate diferentele pentru fiecare stare a variabilei. In acest exemplu se

observa ca sunt 24 de studenti la sectia de marketing; potrivit ipotezei de egalitate a proportiilor, in fiecare sectie ar trebui sa fie 19,3 studenti. In coloana Residual se observa diferenta fata de valorile teoretice: 4,7. Interpretare: valoarea estimata a statisticii χeste semnificativa la un nivel de incredere de 99%, deoarece Sig <0,01, ceea ce conduce la respingerea ipotezei nule. Cele noua categorii de studenti nu au aceeasi proportie; distributia nu este uniforma.