Arbore partial de cost minim

Arbore partial de cost minim

In practica se intalnesc foarte des probleme de tipul urmator: se doreste conectarea unor consumatori la o sursa de energie electrica astfel incat costul bransarii sa fie minim. Transpunand problema in termenii teoriei grafurilor, se cere de fapt determinarea unui arbore partial de cost minim, adica un arbore care are proprietatea ca suma costurilor muchiilor sale sa fie minima.

Definitie Suma costurilor muchiilor unui graf se numeste costul grafului. Daca se defineste functia c:UàR₊ care asociaza fiecarei muchii un numar real numit cost, costul grafului este

Functia c se numeste functia cost.

Fie G=(X,U) un graf conex, reprezentat prin matricea costurilor. Se stie ca prin eliminarea uneia sau a mai multor muchii se obtine un graf partial. Daca graful partial al unui graf G conex este arbore, acesta se numeste arbore partial al lui G. Daca dintr-un graf conex G=(X,U) se elimina muchii astfel incat sa se obtina un arbore partial al carui cost sa fie minim, acesta se numeste arbore partial de cost minim.

Proprietate: Pentru graful G conex, cu functia de cost c, exista un graf partial H conex si de cost minim, care este si arbore.

Pentru un arbore partial de cost minim folosim notatia prescurtata de APM. Pentru determinarea APM sunt cunoscuti mai multi algoritmi, cei mai utilizati fiind algoritmul lui Kruskal (1956) si algoritmul lui Prim, ambii bazati pe o strategie Greedy.

20. Sa se realizeze un program pentru determinarea unui arbore partial intr-un graf simplu cu muchiile ponderate ultilzand algoritmul lui Prim.

Algoritmul lui Kruskal

Se pleaca initial de la n arbori disjuncti, fiecare fiind format dintr-un nod al grafului : H₁, H₂,...,H_n. La fiecare pas vom incerca sa unificam doi dintre arborii existenti, alegerea celor doi arbori ce vor fi unificati facandu-se astfel: dintre toate muchiile nealese inca, se selecteaza muchia de cost minim care are o extremitate intr-un arbore si cealalta extremitate in alt arbore. Prin adaugarea acestei muchii la arborele care se construieste, se vor unifica cei doi arbori disjuncti intr-unul singur. Dupa n-1 pasi se obtine APM care contine n-1 muchii.

Algoritmul pseudocod corespunzator este:

algoritm Kruskal(G,U)

A Æ

pentru fiecare varf vI X(G) executa

Formeaza_Multime(v)

sfarsit pentru

sorteaza muchiile din u in ordinea crescatoare a costului c

pentru fiecare muchie (u,v)IU(G),in ordinea crescatoare a costului executa

daca Gaseste_Multime(u)¹Gaseste_Multime(v) atunci

A A È

Uneste(u,v)

sfarsit daca

sfarsit pentru

returneaza A

Algoritmul foloseste o structura de date pentru multimi disjuncte pentru reprezentarea mai multor multimi de elemente disjuncte. Fiecare multime contine varfurile unui arbore din padurea curenta. Functia Gaseste_Multime(u) returneaza un element reprezentativ din multimea care il contine pe u. Astfel, putem determina daca doua varfuri u si v apartin aceluiasi arbore testand daca Gaseste_Multime(u) este egal cu Gaseste_Multime(v). Combinarea arborilor este realizata de procedura Uneste(u,v).

Pentru a implementa algoritmul lui Kruskal vom reprezenta graful prin vectorul muchiilor, fiecare muchie avand atasat si costul. Pentru a specifica la fiecare pas din ce arbore face parte un nod i, vom folosi vectorul L. Initial, pornim cu n arbori disjuncti, deci L[i]=i , pentru iI . Pentru a eficientiza alegerea muchiilor, vectorul muchiilor u se va ordona crescator dupa costul muchiilor. Pentru a alege cele n-1 muchii ale APM se parcurg elementele vectorului u astfel:

Fie v=[u[i].x,u[i].y] muchia ce urmeaza a fi analizata (plecam cu i=1). Daca in vectorul L extremitatile muchiilor au valori egale, adica L[u[i].x]=L[u[i].y], atunci cele doua extremitati apartin aceluiasi subarbore, deci alegerea acestei muchii ar duce la formarea unui ciclu. In caz contrar, inseamna ca extremitatile muchiei fac parte din subarbori diferiti, fie aceastia H_x si H_y, care pot fi unificati, operatie care presupune ca pentru toate varfurile celor doi arbori trebuie sa apara in vectorul L aceeasi valoare (provenita din primul sau din al doilea arbore). Acest pas se repeta pana am reusit sa alegem cele n-1 muchii ale APM.

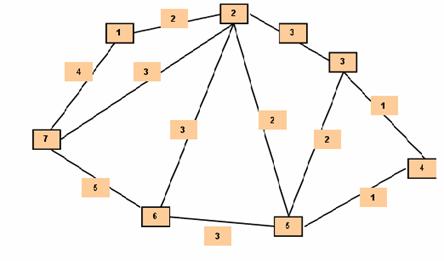Exemplu Fie graful din figura urmatoare:

Pasii algoritmului sunt:

Configuratia initiala:

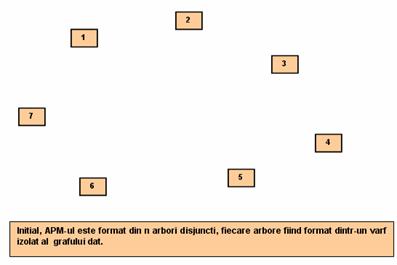Dupa ordonarea crescatoare a muchiilor dupa costul c atasat, avem:

u=([5,4],[3,4],[3,5],[1,2],[2,5],[2,3],[6,5],[2,6],[2,7],[1,7],[7,6])

c=( 1, 1, 2, 2, 2, 3, 3, 3, 3, 4, 5 )

L=(1, 2, 3, 4, 5, 6, 7) , fiecare nod facand parte dintr-un arbore.

Pasul 1:

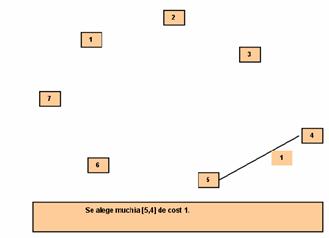Se alege muchia de cost minim [5,4] si L devine: (1,2,3,5,5,6,7) deoarece am unificat arborii H₄ si H₅ si am obtinut subarborele H₅=(4,5). Ceilalti subarbori raman nemodificati.

Pasul 2:

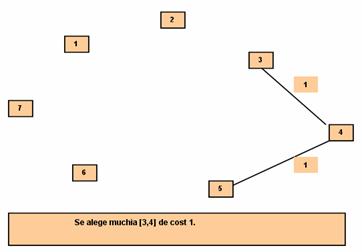Se alege muchia [3,4] de cost minim, unificam H₃ si H₅ si obtinem L=(1,2,3,3,3,6,7) si H₃=(3,4,5).

Pasul 3:

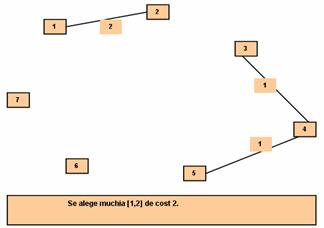Se verifica muchia [3,5] care nu poate fi aleasa deoarece L[3]=L[5] (varfurile 3 si 5 apartin deja aceluiasi subarbore H₃) si alegerea ei ar provoca aparitia unui ciclu.

Se alege muchia [1,2], se unifica H₁ si H₂ si obtinem: L=(1,1,3,3,3,6,7) si H₁=(1,2).

Pasul 4:

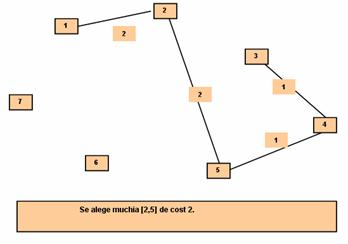Se alege muchia [2,5], se unifica H₁ si H₃ si obtinem: L=(1,1,1,1,1,6,7) si H₁=(1,2,3,4,5).

Pasul 5:

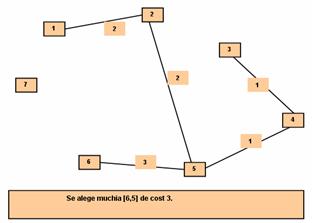Muchia [2,3] nu poate fi aleasa pentru ca ar crea un ciclu.

Se alege muchia [6,5] si se obtine subarborele H₁=(1,2,3,4,5,6).

Pasul 6:

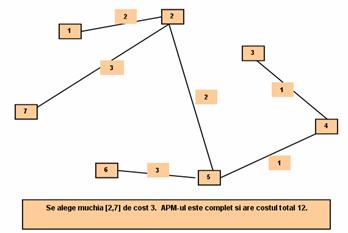Se alege muchia [2,7] si L devine (2,2,2,2,2,2,2), ceea ce corespunde unui arbore partial de cost minim H=([1,2], [2,5], [3,4], [5,4], [6,5], [2,7]), costul total fiind 12.

Nu are importanta care subarbore se alege pentru a transfera varfurile celuilalt subarbore.

Observatie: Daca exista mai multe muchii cu acelasi cost, pentru un graf conex G pot exista mai multe posibilitati de alegere a unei muchii de cost minim, deci pot exista mai multi APM. Acesti arbori se vor deosebi prin muchiile ce vor fi luate in consideratie, si nu prin costul asociat, deoarece aceast cost va fi acelasi pentru toti arborii, si anume ei vor avea cost minim.

Implementarea algoritmului lui Kruskal este:

#include<stdio.h>

#define N 30

#define M 60

typedef struct MUCHIE;

void citire_muchii(MUCHIE u[M],int &n,int &m)

void sortare(MUCHIE u[M],int m)

void creare_apm(MUCHIE u[M],int n,int m)

i++; //trecem la urmatoarea muchie

}

printf('nncostul total este %.2fn',ct);

void main()

Sa se realizeze un program pentru determinarea unui arbore partial economic intr-un graf simplu cu muchiile ponderate ultilzand algoritmul lui Kruskal.

Algoritmul lui Prim

Graful conex este dat prin matricea costurilor, forma 1. La fiecare pas k>0 obtinem un arbore H₁ cu k+1 varfuri si n-(k+1) arbori cu cate un singur varf. La fiecare pas se alege muchia de cost minim care are o extremitate in arborele H₁ deja creat si cealalta extremitate libera. Lucram cu vectorul T in care vom avea, pentru fiecare varf neales inca, varful din H₁ de care acesta se leaga printr-o muchie de cost minim (legatura de tip tata). In componenta corespunzatoare din vectorul Q vom avea costul muchiei adaugate. Cum la inceput avem in H₁ doar varful 1, in toate componentele lui T avem 1, cu exceptia lui T[1], iar in Q, valorile corespunzatoare din linia 1 a matricei costurilor c. La pasul k, dupa alegerea unui nou varf w care se adauga la H₁, se vor actualiza componentele din T si Q pentru varfurile nealese inca deoarece adaugarea varfului w poate modifica aceste valori. Algoritmul are ordinul de complexitate q(n²)

Algoritmul pseudocod corespunzator este:

algoritm Prim(G,c,rad)

Q X(G)

pentru fiecare uIQ executa

D[u]

sfarsit pentru

D[rad]

T[rad]

cat timp Q¹ executa

u Extrage_Minim(Q)

pentru fiecare vIcinilor lui u executa

daca vIQ si c(u,v)<D[v] atunci

T[v] u

D[v] c(u,v)

sfarsit daca

sfarsit pentru

sfarsit cat timp

Se initializeaza coada Q astfel incat acesta sa contina toate varfurile grafului si se initializeaza campul D al fiecarui varf cu ∞, exceptie facand radacina rad, al carei camp D este initializat cu 0. Tatal radacinii se initializeaza cu 0, deoarece rad nu are nici un parinte. Pe parcursul algoritmului, multimea X-Q contine varfurile arborelui curent. Se identifica un varf uIQ incident unei muchii usoare care traverseaza taietura (X-Q,X) (cu exceptia primei iteratii in care u=rad deoarece are cheia D[rad]=0). Eliminarea lui u din multimea Q il adauga pe acesta multimii U-Q a varfurilor din arbore. In liniile urmatoare se actualizeaza campurile D si T ale fiecarui varf v adiacent lui u, dar care nu se afla in arbore. Actualizarea respecta conditiile D[v]=c(v,T[v]) si (v,T[v]) sa fie o muchie usoara care il uneste pe v cu un varf din arbore.

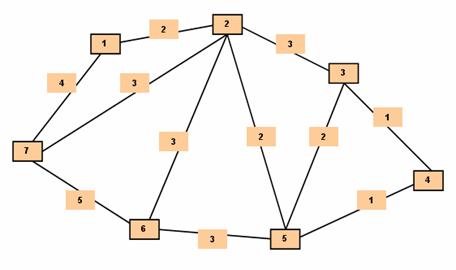Fie graful din figura urmatoare:

Configuratia initiala:

Pasul 1:

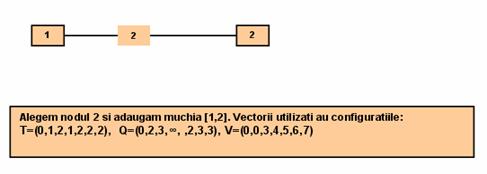
Pasul 2:

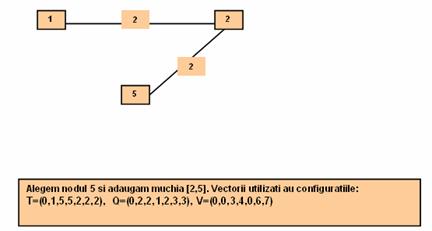
Pasul 3:

   

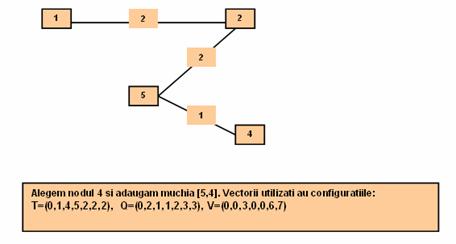
Pasul 4:

   

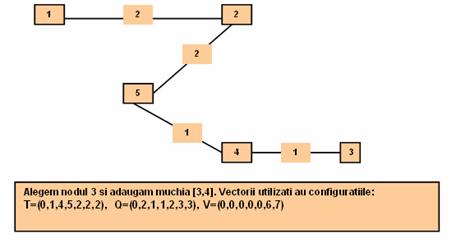
Pasul 5:

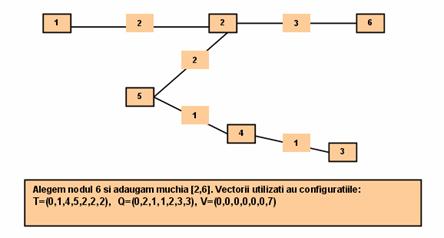
Pasul 6:

   

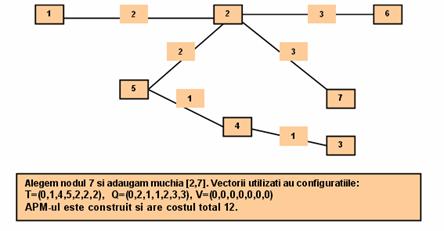
Implementarea algoritmului lui Prim este:

#include<stdio.h>

#define N 30

#define M 60

#define INF 1<<30

void citire_graf(int c[N][N],int &n)

fclose(f);

void creare_apm(int c[N][N],int n)

printf('nnAPM: ');

while(1)

if(min==INF) break;

V[w]=0; //varful w a fost inclus in arbore

printf('[%d,%d] ',T[w],w); //muchia adaugata

ct+=c[T[w]][w]; //actualizam costul arborelui

for(j=2;j<=n;j++)

if(V[j] && Q[j]>c[w][j])

}

printf('ncostul total este %dn',ct);

void main()