CABLURI CU FIBRA OPTICA - CARACTERISTICILE FIZICE ALE FIBREI OPTICE

CABLURI CU FIBRa OPTICa

1. CARACTERISTICILE FIZICE ALE FIBREI OPTICE

1.1. Spectrul electromagnetic

De foarte multi ani, undele electromagnetice se utilizeaza pentru transmiterea de informatii, avantajul real reiese din faptul ca nu au nevoie de un conductor metalic pentru a se propaga, din contra, ele se pot propaga cu viteze ridicate in vid sau in materiale dielectrice.

O prezentare generala a spectrului undelor electromagnetice si a utilizarii lor este redata in figura 1.55. Lumina vizibila nu ocupa decat o plaja restransa de la 380 nm (violet) la 780 nm (rosu). Adiacent, la aceasta plaja se gasesc zonele de radiatii ultraviolete pentru lungimi de unda inferioare si pentru radiatii infrarosii pentru lungimi de unda superioare.

Comunicatiile prin fibra optica utilizeaza lungimi de unda in infrarosu apropiate benzii de la 800 pana la 1600 nm, cu preferinta pentru lungimile de unda de 850, 1300 si 1550 nm (fig.1.55.).

Undele electromagnetice se propaga in vid cu viteza luminii,

c = 299792,456 Km/s.

Valoarea rotunjita la c_o=300000 Km/s=3x10⁵ km/s = 3x10⁸m/s este suficient de exacta pentru a descrie propagarea luminii in aer.

Intr-un mediu fara pierderi si de dimensiune infinita, unda electromagnetica este, ca si lumina, o unda transversala. Campul electric si magnetic al undei transversale oscileaza perpendicular pe directia de propagare.

Daca campul electric sau magnetic oscileaza pe un plan, atunci vectorul campului de intensitate electrica sau magnetica descrie o dreapta. O astfel de unda este numita "unda cu polarizare lineara". Daca proiectia vectorului pe (xoy) descrie un cerc, sau mai general, o elipsa, se vorbeste de o polaritate circulara sau eliptica a luminii.

Frecventa joasa Inalta frecventa Microunde

Curent alternativ tehnic unde unde unde unde dm cm

lungi medii scurte metrice

10⁷m 10⁸m 10Km 10Km 1Km 100m 10m 1m 1m 1cm

10Hz 100Hz 1K 10K 100K 1M 10M 100M 1G 10G

Radioemisie

Teleemisie

Sateliti

Microunde

mm

1cm 1mm 100 m 10 m 1 m 100nm 10nm 1nm 100pm 10pm 1pm

10G 100G 1T 10T 100T 10¹⁵ 10¹⁶ 10¹⁷ 10¹⁸ 10¹⁹ 10²⁰ Hz

infrarosu ultraviolet

raze X

razeY

1,6 m 1,6 1,4 1,3 1,2 1,1 1 900 800 700 600 500 400

spectru utilizat pe fibre optice

lumina vizibila

Fig.1.55. Spectrul undelor electromagnetice.

Figura 1.56. arata diferite tipuri de polarizare ale unei unde luminoase care se propaga pe directia z.

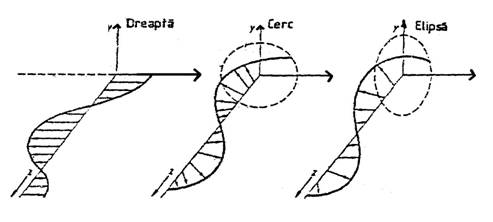
Fig. 1.56. Tipuri de polarizare.

1.2. Termeni tehnici fundamentali in teoria undelor

In general, consideram o unda ca fiind propagarea unei stari sau a unei excitatii intr-un mediu, fara ca masa sau materia acestui mediu sa fie transportate. In cazul undei luminoase, starea este campul electromagnetic care se propaga intr-un mediu transparent optic.

O functie sinusoidala descrie forma cea mai simpla a propagarii in timp si spatiu. Pentru o unda plana, care se propaga in directia z, se poate scrie pentru deviatia a:

a = A sin (ωt - kz) = A sin 2π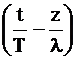

unde:

a = deviatia undei plane,

A = amplitudinea,

ω = frecventa unghiulara, in s^-1,

t = timpul, in s,

k = numarul de unda, in m^-1,

z = lungimea in directia z, in nm,

T = perioada de oscilatie, in s,

λ = lungimea de unda, in m.

Amplitudinea A a undei descrie deviatia maxima plecand de la pozitia de repaus.

Valoarea dintre paranteze (ωt-kz) este numita unghiul fazei sau prescurtat "faza de unda". Unghiul de faza j este masurat in radiani (rad), de exemplu:

1 rad =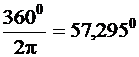

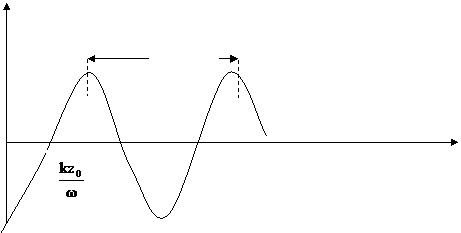
Pentru a ilustra aceasta, figura 1.57 arata o unda plana in functie de timp la un punct fix, z = z₀. Putem vedea ca punctele a₁ si a₃ sunt in aceeasi faza de oscilatie

Diferenta lor de faza este de 2 π. Punctul a₂ are aceeasi deviatie precum a₁ si a₃ dar se gaseste in alta faza.

Marimea ω este numita frecventa unghiulara. Ea este egala cu frecventa inmultita cu 2 π; frecventa fiind numarul de oscilatii in unitatea de timp:

ω = 2 π f, unde f este frecventa in Hz.

A

T=

z₁ z₂ z₃

t

Fig. 1.57. Unda armonica plana pentru z = z₀.

T reprezinta durata de oscilatie, deci timpul unei oscilatii complete sau perioada de oscilatie. Frecventa f este invers proportionala cu perioada de oscilatie T.

k este numarul de unda ce este egal cu modulul vectorului de unda k care indica directia de propagare a undei. Numarul de unda k indica deplasarea de faza a undei pe unitatea de lungime si este, astfel, invers proportional cu lungimea de unda, constanta de proportionalitate fiind 2π:

k=2π/ λ.

Lungimea de unda λ este perioada spatiala de unda, deci, distanta strabatuta de o suprafata de unda in timp de o perioada.

O relatie fundamentala exista intre frecventa, lungimea de unda λ si viteza de propagare c a unei unde: c = f λ.

1.3. Reflexia

Daca lumina cade pe suprafata de separatie dintre doua medii, apare fenomenul de intoarcere (partiala), in mediul din care au venit a radiatiilor ondulatorii sau corpusculare.

Cantitatea de lumina reflectata depinde de unghiul α₁ care este format de raza incidenta cu axa de incidenta (normala la suprafata de separatie). Raza luminoasa reflectata formeaza un unghi α₂ cu axa incidenta (figura 1.57.).

Raza reflectata:

- ramane in planul de incidenta format de raza incidenta si axa de incidenta;

- este situata pe partea opusa a axei de incidenta in raport cu raza incidenta;

- formeaza cu axa de incidenta un acelasi unghi: α₁ = α_2.

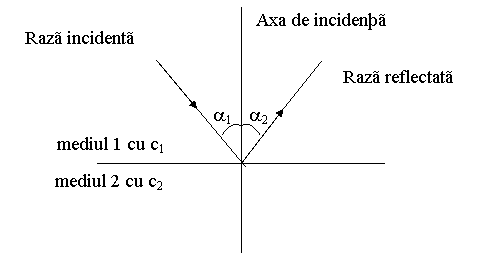
Fig. 1.57. Reflexia luminii.

1.4.Refractia

Daca o raza luminoasa trece oblic, cu un unghi de incidenta α, dintr-un mediu mai putin dens (exemplu aerul) intr-un mediu mai dens (exemplu sticla) sau invers, atunci directia sa este schimbata in raport cu axa de incidenta, formand un unghi β cu aceasta axa.

In cazul materialelor izotrope, materiale avand proprietati identice in toate directiile, se aplica legea de refractie a lui Snell: raportul dintre sinusul unghiului de incidenta si sinusul unghiului de refractie este constant si egal cu raportul c₁/c₂; c₁ si c₂ sunt vitezele de propagare a luminii in mediile 1 si 2.

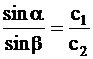, unde:

unghiul de incidenta,

unghiul de refractie,

c₁ = viteza luminii in mediul 1,

c₂ = viteza luminii in mediul 2.

In cazul a doua medii transparente, consideram mediul cel mai dens, cel in care viteza de propagare este mai lenta.

Daca consideram trecerea unei raze luminoase din vid , unde viteza de propagare este c₀, intr-un mediu unde viteza de propagare este c, relatia este :

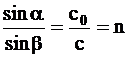
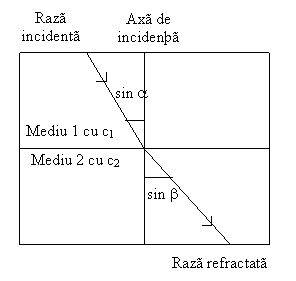
Fig.1.58. Refractia luminii.

Acest raport este numit "indice de refractie n" si este constanta proprie materialelor respective.

Indicele de refactie al vidului este aproximativ egal cu al aerului avand valoarea 1.

Pentru doua medii cu indici de refractie n₁ si n₂ si viteza de propagare a luminii c₁ si c₂ putem scrie:

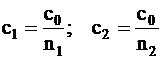
Prin deductie, se ajunge la o forma diferita a legii refractiei a lui Snell:

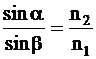
Raportul dintre sinusul unghiului de incidenta si sinusul unghiului de refractie este invers proportional cu raportul indicilor de refractie.

Aplicatie:

Pentru un indice de refractie n₁ = 1,5, o valoare tipica pentru sticla fibrei optice, viteza de propagare c₁ in fibra este egala cu:

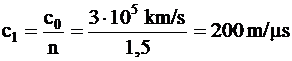
respectiv 5 ms pentru 1 km de fibra optica sau 5ns pentru 1 m de fibra optica.

Indicele de refractie n al unui material depinde fundamental de lungime de unda a luminii; pentru sticla de cuart si in gama de unde infrarosii, care este importanta pentru comunicatiile optice, indicele de refractie descreste proportional cu cresterea lungimii de unda.

Valoarea n este valabila pentru unde care se propaga cu o singura lungime de unda si cu o amplitudine constanta, deci care nu pot transmite informatii. Pentru ca informatia sa poata fi transmisa, aceste unde trebuie modulate. Pentru comunicatii optice digitale se utilizeaza impulsuri de lumina. Aceste impulsuri sunt scurte grupuri de unde, formate din unde luminoase cu lungimi de unda diferite.

In aceste grupuri undele individuale se propaga cu viteze diferite. Viteza de propagare a unui astfel de grup de unde este numita "viteza de grup". Relatia intre indicele de refractie de grup n_g si indicele de refractie n este:

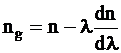
Cateva valori tipice se gasesc in tabelul 1.11.

Indicele de refractie de grup n_g este considerat mai mare decat indicele de refractie n pentru toate lungimile de unda.

Tabelul 1.11. Indice de refractie nl si indice de refractie de grup n_gl 100% SiO_2.

Pentru a calcula timpul de propagare al semnalelor optice, trebuie utilizat doar indicele n_g. Este de remarcat faptul ca indicele de refractie de grup atinge un minim in jurul unei valori de lungime de unda de 1300 nm. Asa cum am vazut inainte, aceasta gama de unde prezinta un interes deosebit in transmisia pe fibra optica.

1.5. Reflexia totala

Daca o raza luminoasa (3) trece sub unghiuri de incidenta crescande dintr-un mediu mai dens (cu un indice de refractie n₁)

dintr-un mediu mai putin dens (cu un indice de refractie n₂), se poate ajunge ca pentru un unghi de incidenta α₀, unghiul de refractie sa fie β₀=90⁰ (fig.1.59).

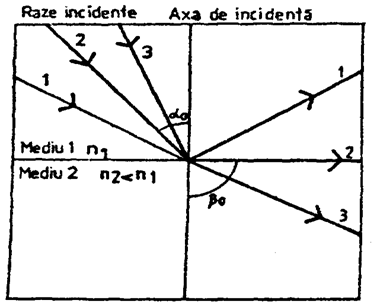
1-reflexia totala a razei incidente; 2- raza refractata sub un

unghi de refractie β₀=90⁰; 3- raza refractata.

Fig. 1.59. Reflexia totala a luminii.

In acest caz, raza luminoasa (2) se propaga in paralel cu suprafata de separare dintre cele doua medii. Unghiul de incidenta este numit unghi limita.

Pentru unghiul limita α₀ are valabila relatia urmatoare:

sin α₀ =

Aceasta inseamna ca unghiul limita depinde de raportul indicilor de refractie n₁ si n₂ ai celor doua medii.

Aplicatie:

Unghiul limita dintre apa ( n₁ = 1,333) si aer ( n₀ = 1) este egal cu:

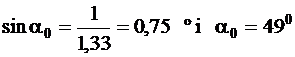
Intre sticla (n₁ = 1,5 ) si aer (n₀ = 1) obtinem:

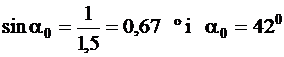
Pentru toate razele luminoase avand unghiul de incidenta α mai mare ca unghiul limita α₀, nu mai exista raze refractate in mediul mai putin dens. La suprafata de separare dintre cele doua medii aceste raze luminoase se rasfrang in mediul mai dens.

Acest fenomen este numit reflexie totala (raza luminoasa 1 din figura 1.59). Reflexia totala poate avea loc doar in cazul trecerii unei raze luminoase dintr-un mediu mai dens (de exemplu sticla cu n₁=1,5) intr-un mediu mai putin dens(de exemplu aer cu n₂=1); invers nu este posibil.

1.6. Apertura numerica

Intr-o fibra optica se foloseste fenomenul reflexiei totale pentru a ghida raza luminoasa. Acest ghidaj se obtine instaland un miez de sticla (indice de refractie n₁) inconjurat de un invelis de sticla (indice de refractie n₂), n₁ fiind putin mai mare ca n₂ (fig. 1.60).

Analizand expresia 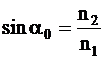putem concluziona ca toate razele luminoase care nu deviaza mai mult de ( 90⁰ - ) fata de axa fibrei vor fi ghidate prin sticla miezului.

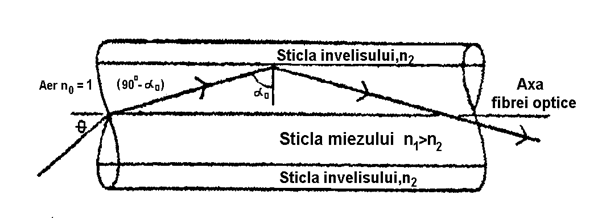
Fig. 1.60. Ghidarea luminii intr-o fibra optica.

Injectand din exterior (aer, indice de refractie n₀=1) o raza luminoasa in sticla miezului, unghiul de injectie dintre raza luminoasa si axa fibrei poate fi determinat aplicand legea refractiei:

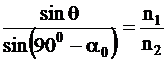, aceasta implicand:

.

Conditia pentru unghiul limita (sin =n₂/n₁) ne conduce la expresia:

.

Unghiul de injectie maximal este numit "unghiul de acceptanta" al fibrei optice; el depinde doar de indicii de refractie n₁ si n₂.

Sinusul unghiului de acceptanta este numit apertura numerica (1) a fibrei optice:

Aceasta valoare este de o importanta esentiala pentru injectia luminii in fibra.

1.7. Propagarea luminii in fibra optica

Legile optice permit descrierea reflexiei totale la suprafata de separatie dintre miez-invelis a fibrei optice.

Pentru a efectua o analiza mai detaliata a posibilitatilor de propagare ale luminii in miezul sticlei, trebuie sa consideram fenomenele opticii ondulatorii; aceasta devine necesar datorita diametrelor caracteristice miezurilor fibrelor, cuprinse intre 10 si 100 mm si care sunt, in consecinta, cu putin mai mari decat lungimea de unda a luminii transportate, care e in jur de 1mm.

Datorita acestui fapt, anumite fenomene de interferenta care apar nu pot fi aplicate decat cu ajutorul teoriei optice ondulatorii.

Superpozitia a doua sau mai multe unde si combinarea lor intr-una singura este, in general, numita interferenta.

O manifestare tipica a interferentei a doua unde este obtinuta cand ele au aceeasi lungime de unda si cand exista un defazaj constant intre ele. Astfel de unde se numesc unde coerente. Daca intr-un punct din spatiu, cele doua unde difera in faza lor, printr-un multiplu par al lungimii de unda l, atunci are loc o insumare a amplitudinilor. Pe de alta parte, in cazul unei defazaj egal cu un multiplu al jumatatii de unda (l/2) se produce o scadere, iar in cazul a doua unde avand aceeasi amplitudine, are loc o anulare locala a undelor.

Daca consideram doua surse luminoase obisnuite (becuri electrice) si le suprapunem lumina, nu observam nici un tip de interferenta pentru ca lumina lor e incoerenta. Acest fapt e datorat procesului de emisie a luminii (in exemplu precizat filamentele fluorescente).

In cazul fenomenelor spontane si aleatorii, fiecare atom al filamentelor incandescente emite " flash-uri " de lumina care au serii de unde cu o durata de viata in jur de 10^-8s. Considerand ca viteza luminii in aer este 3 10⁸ m/s, aceste serii de unde au o lungime de 3 m. Aceasta lungime este numita "lungime de coerenta". Suprapunerea acestor serii de unde este complet neregulata si ocazioneaza doar iluminarea globala a spatiului inconjurator.

Pentru transmisia pe fibre optice este necesar sa se gaseasca o sursa luminoasa cat mai coerenta. Prin urmare, largimea spectrala va trebui sa fie cat mai mica. Spre deosebire de diodele electroluminiscente, dioda laser ofera, gratie unei emisii stimulate, o diferenta de faza constanta la o aceeasi lungime de unda. Prin urmare, fenomenele de interferenta apar in ghidul de unda, ceea ce poate fi constatat din faptul ca lumina se propaga doar sub unghiuri bine determinate in miezul fibrei; prin "determinate" intelegandu-se ca propagarea are loc in directii in care undele luminoase sunt amplificate prin suprapunerea lor si prezinta o interferenta constructiva. Undele luminoase capabile sa se propage intr-o fibra optica sunt numite moduri (unde naturale).

Aceste moduri pot fi determinate matematic, mai precis prin ecuatiile lui Maxwell.

Acest sistem de ecuatii, de obicei utilizat pentru unde electromagnetice, poate fi simplificat in mod considerabil in ceea ce priveste fibrele optice, daca nu tinem seama decat de undele slab ghidate.

Este vorba de unde care se propaga aproape in directia axiala a fibrei si care prezinta o intensitate neglijabila a campului, in lungul axei. Ele apar daca indicii de refractie ai sticlei miezului n₁ si sticlei invelisului n₂ nu difera decat foarte putin.

Masura acestei diferente in refractie este diferenta relativa de indice D, definita astfel:

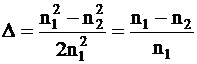
Pentru o fibra optica diferenta relativa de indice D este foarte mica in raport cu unitatea si, datorita acestui fapt, nu are loc decat un ghidaj slab al undelor luminoase in sticla miezului.

Solutiile ecuatiilor simplificate ale lui Maxwell ofera foarte bune aproximari pentru modurile care se propaga in fibra optica. Figura 1.61. da ca exemplu distributia intensitatii luminoase in sectiunea transversala a fibrei optice pentru primele 10 moduri. Undele naturale oscileaza pe un singur plan si ele sunt polarizate liniar. Denumirea lor este LP νμ cu cei doi indici modali ν si μ .

Valoarea lui ν este indicele modal azimutal si indica jumatatea numarului de puncte luminoase pe inel luminos concentric.

Valorile lui ν pot fi 0,1,2,3,, si pentru ν = 0, fiecare inel luminos exista fara subdiviziuni.

Valoarea lui ν este indicele modal radical si indica numarul de inele luminoase concentrice ale modului; μ poate lua valorile 1,2,3,

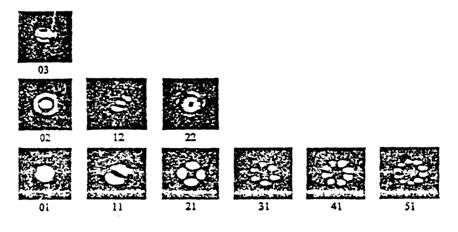
Figura 1.61. Primele 10 moduri LP ale unei fibrei optice.

Modul fundamental este numit LP₀₁, ordinul superior fiind LP₁₁.

2. PROFILELE FIBREI OPTICE

Daca indicele de refractie n al unei fibre optice este considerat in functie de raza r, atunci vom vorbi despre profilul indicelui de refractie al fibrei. Astfel descriem variatia radiala a indicelui de refractie, incepand pe axa fibrei si mergand spre exteriorul invelisului:

n = n(r)

Propagarea modurilor in fibra optica depinde de forma profilului indicelui de refractie (fig. 1.62.).

In practica, suntem interesati sa consideram profilele de indice definite prin legi (expresii) exponentiale. Se studiaza profilele de indice prin refractie pentru care variatia radiala a indicelui urmeaza o lege (expresie) de forma:

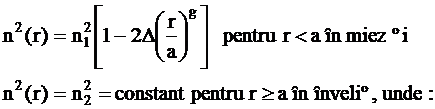
n₁ = indice de refractie pe axa fibrei (r = 0);

D = diferenta relativa de indice;

r = distanta radiala de la axa fibrei, in mm; r I [0,a];

a = raza miezului fibrei, in mm;

g = puterea, numita si exponentul profilului;

n₂ = indice de refractie al undei invelisului.

Diferenta relativa de indice depinde de apertura numerica si de indicii de refractie n₁ si n₂.

Merita sa fie mentionate urmatoarele cazuri exceptionale (fig.1.62)

g = 1: profil triunghiular;

g = 2: profil parabolic;

g : profil cu indice in treapta (caz limita).

Doar in ultimul caz (pentru profilul de indice in treapta) - indicele de refractie n(r)=n₁ este constant in miez. Pentru toate celelalte profile cu indice de refractie in miez, n(r) creste proportional de la valoarea n₂ in invelis, la valoarea n₁ pe axa fibrei.

Din acest motiv, aceste profile sunt denumite " profile cu indice gradat". Aceasta denumire a fost special adoptata pentru profilul parabolic (cu g = 2), deoarece aceste fibre optice au proprietati tehnice bune in ghidarea luminii.

O alta valoare importanta care descrie fibra optica este parametrul V, numit frecventa normala de taiere. Ea depinde de raza a, de apertura numerica A_N a sticlei miezului, de lungimea de unda λ si de numarul de unda k. Parametrul V este adimensional:

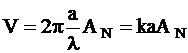unde:

a = raza miezului;

λ = lungimea de unda;

A_N = apertura numerica;

k = numarul de unda.

Numarul N de moduri ghidate prin sticla miezului depinde de acest parametru; pentru un profil de indice la o putere oarecare cu un exponent de profil g exista urmatoarea relatie:

.

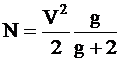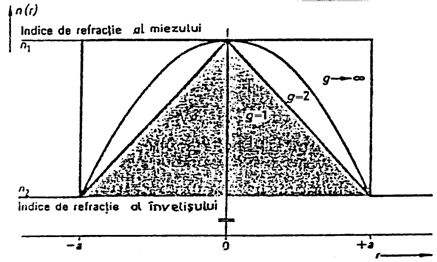
Fig. 1.62. Profilul indicelui de refractie al unei fibre optice

Pentru profilul cu indice treapta (g ) numarul de moduri ghidate este aproximativ:

N.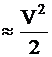

Pentru profilul cu indice gradat, numarul de moduri este aproximativ:

.

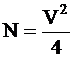Aplicatie:

O fibra optica cu indicele gradat (g = 2), avand un diametru al miezului 2a = 50 μm, o apertura numerica A_N = 0,2, are ca frecventa normata V, pentru o lungime de unda λ=1 μm:

.

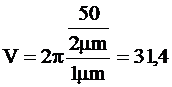Numarul N de moduri ghidate in miezul fibrei este atunci:

N.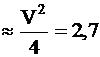

Fibra optica care ghideaza mai multe moduri este numita fibra optica multimod.

Daca vrem sa reducem numarul de moduri, adica sa reducem parametrul V, trebuie sa micsoram diametrul miezului 2a, fie sa micsoram apertura numerica sau sa marim lungimea de unda λ.

Intrucat cantitatea de lumina care poate fi injectata in fibra depinde, in mod substantial, de apertura numerica, aceasta trebuie sa ramana atat de mare cat este posibil. Reducerea razei miezului a, este limitata, deoarece manipularea si tehnica conexiunilor devin din ce in ce mai dificile. Pe de alta parte, devine dificila constructia surselor si detectoarelor pentru lungimi de unda mai mari si, prin urmare, o crestere substantiala a lui λ nu este posibila.

Daca pentru o fibra optica cu indice in treapta (g ) parametrul V devine mai mic decat constanta V_C = 2,405, atunci un singur mod, modul fundamental LP_01,   se poate propaga. Numim o astfel de fibra optica fibra optica monomod.

Constanta V_C reprezinta o valoare limita pentru fibra optica cu indice de treapta (g ). Indicele c provine din cuvintele englezesti cut-off value. Pentru un profil de indice, valoarea limita V_c se calculeaza cu relatia:

.

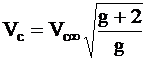Pentru o fibra optica cu indice gradat (g = 2), valoarea limita V_c este aproximativ:

.

Aplicatie:

O fibra optica cu indice in treapta cu un diametru al miezului 2a = 9 μm si o apertura numerica A_N = 0,11 atinge frecventa normata V=V_c pentru o lungime de unda de:

.

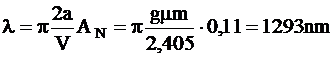Lungimea de unda l calculata, careia ii apartine valoarea limita V_c este numita " lungime de unda de taiere"l_c

.

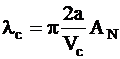Pentru toate lungimile de unda λ_c, doar un singur mod este in stare sa se propage in miezul unei fibre considerate. Aceasta fibra este, deci, o fibra optica monomod pentru toate lungimile de unda superioare lui λ_c.

Drept urmare a polarizarii luminii, modul fundamental si toate modurile de ordin superior sunt constituite din doua moduri care oscileaza perpendicular unul in raport cu celalalt. Efectele acestor moduri polarizate nu sunt importante decat pentru aplicatiile speciale ale fibrelor optice care mentin polaritatea (tehnici de detectare optica, busole cu fibra optica). Efectele datorate separarii in doua moduri sunt, in prezent, nesemnificative pentru tehnica cablurilor optice si pentru tehnologia comunicatiilor. Aceasta este ilustrata de faptul ca se vorbeste despre fibre optice monomod, in ciuda prezentei celor doua moduri polarizate.

2.1. Profil cu indice in treapta

Pentru ca lumina sa fie ghidata in sticla miezului unei fibre optice cu indice in treapta, trebuie ca la interferenta miez-invelis indicele de refractie n₁ al miezului sticlei sa fie usor superior indicelui de refractie al invelisului sticlei n₂. Daca indicele de refractie n₁ al sticlei miezului este constant pe toata sectiunea transversala a miezului, vorbim de profil cu indice in treapta, caci indicele de refractie creste la interfata invelis-miez in forma de treapta si ramane apoi constant. Figura 1.63. arata profilul de refractie al unei fibre optice cu indice in treapta si traiectoria unei raze luminoase cu unghiurile corespunzatoare.

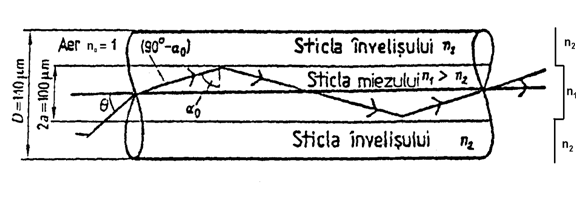
Fig.1.63. Fibra optica cu indice in treapta

Astfel de fibra optica este numita "fibra optica cu indice in treapta". Aceasta fibra poate fi fabricata simplu, dar ea este utilizata mai rar in prezent. Pentru a descrie mai bine propagarea luminii in fibra optica, s-a ales exemplul urmator (fig. 1.63.).

Dimensiunile tipice ale unei fibre multimod cu indice in treapta:

- diametrul miezului (2a) 100 mm;

- diametrul invelisului (D) 140 mm;

- indicele de refractie al miezului (n₁)

- indicele de refractie al invelisului (n₂)

In exemplul considerat, unghiul limita a al reflectiei totale, adica unghiul cel mai mic dintre o axa luminoasa si axa de incidenta la care aceasta raza este ghidata de sticla miezului, fara a fi reflectata in invelis este:

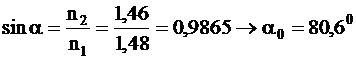
Toate razele luminoase care formeaza un unghi mai mic sau egal cu (90⁰-a ) = 9,4⁰ cu axa fibrei optice, sunt ghidate prin sticla miezului.

Daca se injecteaza in sticla miezului o raza luminoasa din exterior (aer, n₀= 1), trebuie sa se tina seama de legea refractiei si in consecinta in fibra nu pot patrunde decat razele cuprinse intr-un con de acceptanta cu un unghi q determinat. Pentru exemplul nostru, acest unghi se calculeaza astfel:

,

deci q

Cum sinusul unghiului de acceptanta este, prin definitie, egal cu apertura numerica, rezulta pentru A_N:

A_N = sinq

Diferenta relativa de indice D este pentru aceasta fibra optica:

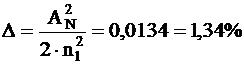
La o lungime de unda l = 850nm, frecventa normata V se calculeaza pentru o fibra optica cu indice in treapta, cu un diametru al miezului 2a = 100 mm, dupa cum urmeaza:

.

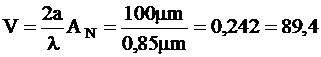Numarul de moduri este atunci aproximativ:

.

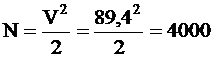O astfel de fibra optica este numita fibra optica multimod. Un "flash" de lumina propagandu-se intr-o astfel de fibra este format din numeroase alte "flash-uri" partiale, transportate in fiecare din modurile conductorului. La inceputul fibrei optice, fiecare din aceste moduri este excitat sub un unghi de injectie diferit si ghidat de sticla miezului dupa traiectoriile respective. Fiecare mod parcurge fibra pe o traiectorie diferita si ajunge, astfel, la extremitatea conductorului in timpi diferiti. Raportul intre timpul de propagare cel mai lung si timpul de propagare cel mai scurt este direct proportional cu raportul indicilor de refractie intre invelis si miez, adica este de ordinul diferentei relative de indice D (mai mult de 1%).

Aplicatie:

Lumina parcurge aproximativ in 5ms o fibra cu indice in treapta cu lungimea de 1Km. Timpul de intarziere Dt este aproximativ:

Dt = 5 ms 0,01 = 50 ns.

Distorsiunea care produce diferentele de timp in modurile individuale este numita "dispersie modala". Ea este cauza aparitiei unui impuls luminos de scurta durata pe timpul trecerii printr-o fibra cu indice in treapta. Dispersia modala afecteaza calitatea comunicatiilor optice deoarece reduce viteza de transmisie (debitul binar) sau largimea benzii de transmisiune. Acest efect este moderat pentru ca modurile individuale se influenteaza unul pe altul si schimba energia in lungul traiectoriilor lor. Acest amestec de moduri sau cuplaj de moduri se produce cu o intensitate particulara in locuri cu neregularitati ale sticlei miezului, la imbinari si la curburi ale fibrei.

Daca se observa traiectoria modurilor in lungul axei fibrei optice, se constata ca, prin schimb de energie, are loc o transformare a modurilor de ordin inferior (cu un unghi > 90⁰ intre mod si axa fibrei) in moduri de ordin superior (cu un unghi ascutit intre mod si axa) si invers. Rezulta, prin urmare, o compensare a vitezelor de propagare a modurilor.

Prelungirea in timp Dt a impulsului injectat nu este deci o functie liniara depinzand de lungimea fibrei (Dt proportional cu L), ci, in cazul ideal, este in functie de radicalul lungimii (proportional cu).

Dispersia modala poate fi eliminata complet daca fibra cu indice in treapta este dimensionata astfel incat un singur mod sa se poata propaga, in principiu modul fundamental LP₀₁.

Dar modul fundamental sufera de asemenea o imprastiere in timpul cand este parcursa fibra optica. Acest fenomen este numit dispersie cromatica. Fiind o proprietate a materialului, ea se manifesta, in general, pentru toate fibrele optice. Totusi, comparata cu dispersia modala, dispersia cromatica este relativ mica sau chiar nula, pentru o gama de unde cuprinsa intre1200 nm si 1600 nm.

Termenul "diametrul" al campului de mod "2W₀" a fost introdus pentru cuantificarea valorii (amplitudinea radiala a campului) modului fundamental.

Pentru obtinerea unei fibre optice cu indice in treapta si cu pierderi mici, care ghideaza doar modul fundamental in zona superioara lui 1200 nm, trebuie sa se reduca diametrul campului de mod 2W₀ pana la aproximativ 10 m. O astfel de fibra optica cu indice in treapta este numita fibra optica monomod.

Dimensiuni tipice pentru fibre optice monomod:

- diametrul campului de mod (2W₀) = 10 mm;

- diametrul invelisului (D) = 125 mm;

- indicele de refractie maxim (n₁) 1,46;

- diferenta relativa de indice D

Profilul indicelui de refractie si traiectoria unei raze luminoase pentru o fibra optica monomod sunt prezentate in figura 1.64.

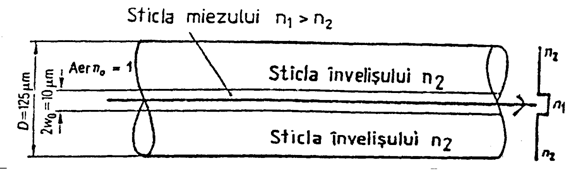
Fig. 1.64. Fibra optica monomod.

Apertura numerica A_N a unei fibre optice monomod este data de:

cu unghi de acceptanta q de:

q = A_N

q

Trebuie notat ca intr-o fibra monomod, nu numai diametrul miezului dar si apertura numerica si deci unghiul de acceptanta, sunt mult mai mici, comparate cu o fibra optica multimod. Din acest motiv injectia de lumina devine relativ dificila.

Pentru o fibra optica monomod tipica (avand o frecventa normata V = V_c = 2,405), lungimea de unda de taiere l_c (de la valoarea sa in sus se propaga numai modul fundamental) este definita de:

.

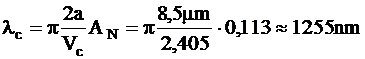Pentru aceasta lungime de unda l_c, modul urmator LP₁₁ (fig. 1.65 si 1.66) nu se mai poate propaga in fibra dar modul fundamental LP₀₁ se mai propaga la lungimi de unda mai mari si campul sau de mod se extinde in sticla invelisului (fig. 1.65).

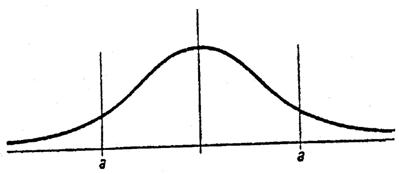
Fig. 1.65. Distributia radiala a campului modului fundamental LP₀₁.

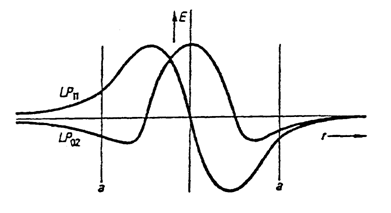
Fig. 1.66. Distributia radiala a campului la modurile LP₁₁ si LP₀₂.

Aplicatie:

O fibra monomod cu indice in treapta cu un diametru al campului de mod 1W₀ = 10 mm si o lungime de unda de taiere l_c = 1255 nm.

(V_c = 2,405) are pentru diametrul miezului 2a si lungimi de unda de 1300 si 1550 nm, urmatoarele valori:

,

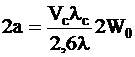pentru l = 1300 nm:

,

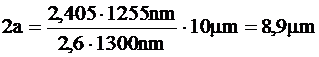pentru l = 1550 nm:

.

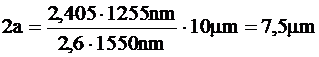Dimensiunile campului de mod reprezinta un factor important in ceea ce priveste atenuarea fibrelor monomod curbate sau sudate. Astfel, un camp de mod mai puternic provoaca un ghidaj mai slab al undelor luminoase la curburi, dar pierderi mai mici la suduri si la conexiuni.

2.2. Profil cu indice gradat

Intr-o fibra optica cu indice in treapta multimod, modurile se propaga pe traiectorii mai mult sau mai putin lungi si ajung la capatul fibrei in timpi diferiti. Aceasta dispersie modala nedorita poate fi serios redusa, variind indicele de refractie in lungul razei miezului fibrei conform unei legi parabolice. Valoarea maxima n₁ a indicelui de refractie se gaseste pe axa fibrei si este redusa gradat, pentru a atinge valoarea n₂ in sticla invelisului.

Un astfel de profil cu indice gradat sau profil cu indice variind dupa o lege exponentiala cu un exponent de profil g = 2 este definit de:

n² (r) = 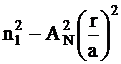pentru r < a la miez;

si n² (r) = pentru r a in invelis.

Un ghid de unda cu acest profil cu indice gradat este de asemenea numit fibra optica cu indice gradat.

Dimensiuni tipice pentru o fibra cu indice gradat:

- diametrul miezului (2a) = 50 mm;

- diametrul invelisului (D) = 125 mm;

- indice de refractie maxim (n₁) = 1,46;

- diferenta relativa de indice (D

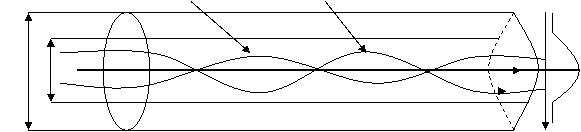
Figura 1.67 arata traiectoriile undelor luminoase de ordin diferit si profilul de refractie al unei fibre cu indice gradat.

Moduri de ordin inferior Moduri de ordin superior

n₂

Asrn Sticla invelisului, n₂ p

Sticla miezului n_r>n₂

Sticla invelisului, n₂ p n₂

Figura 1.67. Fibra optica cu indice gradat

Razele luminoase urmaresc traiectorii curbilinii de forma ondulata sau elicoidala, invers de ceea ce se intampla in profilele cu indice in treapta unde ele se propaga in zig-zag. Ca urmare a schimbarii continue a indicelui de refractie n(r) in sticla miezului, razele sunt in permanenta refractate si directia lor de propagare se schimba, deci ele se propaga pe traiectorii ondulatorii.

Razele care oscileaza in jurul axei fibrei au totdeauna de parcurs traiectorii mai lungi decat raza care se propaga in jurul axei dar, ca urmare a diminuarii indicelui de refractie dincolo de axa ele se propaga cu viteze mai ridicate si exista, in acest fel, compensare. De fapt, timpii de intarziere dispar aproape complet. Daca forma parabolica a profilului este fabricata cu suficienta precizie, nu se mai observa, pe o distanta de 1 Km si deci pentru un timp de propagare al luminii de 5 ms, decat timpii de intarziere in jur de 0,1 ns.

Acest timp de intarziere, minim pentru fibrele cu indice gradat, este datorat nu numai dispersiei materialului ci si dispersiei profilului. Aceasta isi gaseste explicatie in faptul ca indicii de refractie intre miez si invelis variaza in diferite feluri in functie de lungimea de unda si, prin urmare, atat diferenta relativa de indice D cat si exponentul de profil g, sunt functie de lungimea de unda.

Exponentul de profil optim g pentru un profil cu indice gradat parabolic, poate fi calculat in mod teoretic cu expresia:

g = 2 - 2P - D(2-P).

Parametrul P < 1 si diferenta relativa de indice D, depind de lungimea de unda, deci, exponentul de profil g depinde si el de aceasta lungime de unda.

Trebuie notat ca pentru un profil cu indice gradat cu g = 2, timpii de propagare ai modurilor nu pot fi aproape identici decat intr-o plaja de lungimi de unda redusa.

Pentru ca indicele de refractie n(r) al unei fibre optice cu indice gradat depind de distanta radiala r de la axa fibrei, unghiul de acceptanta q, care este important pentru injectia luminii este, de asemenea, o functie de r:

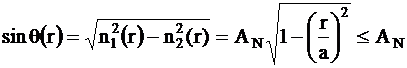
Unghiul de acceptanta isi atinge maximul pe axa fibrei (r=0) si este egal cu apertura numerica A_N. La suprafata de separare miez-invelis (r=a) acest unghi este egal cu zero.

Apertura numerica a unei fibre optice cu indice gradat este:

si unghiul de acceptanta maxim q_max pe axa fibrei este egal cu:

sinq_max = A_N

iar q

Asa cum s-a dovedit, coordonatele sin²q si r² sunt cele mai favorabile pentru reprezentarea unghiului de acceptanta q in functie de distanta r de la axa fibrei. Un astfel de sistem de coordonate este numit diagrama faza-spatiu. Figurile 1.68 si 1.69 compara diagramele unei fibre optice cu indice gradat si ale unei fibre cu indice in treapta.

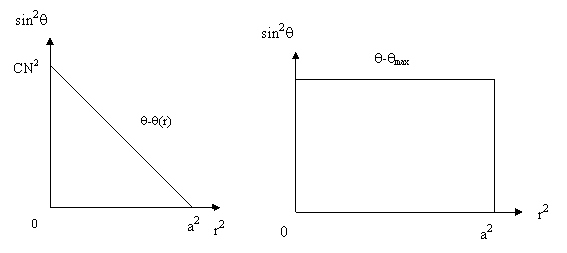
Fig. 1.68. Diagrama faza - spatiu Fig. 1.69. Diagrama faza - spatiu

a unei fibre optice cu indice gradat  a unei fibre optice cu

indice in treapta

Suprafata limitata de curba unghiului de acceptanta maxim q_max este proportionala cu puterea optica pe care o putem injecta in miezul fibrei. Puterea optica injectabila intr-o fibra cu indice in treapta face cat dublul puterii injectabile intr-o fibra cu indice gradat, cu conditia ca apertura numerica A_N si raza miezului a, sa fie identice pentru cele doua fibre. Numarul N de moduri ghidate de miez este, astfel, proportional cu aceasta suprafata. Modurile individuale pot fi localizate in interiorul acestei arii.

Astfel modurile LP_nm de ordin inferior cu indici modulari v = 0,1,2, si m=1,2 si care se propaga aproape paralel in raport cu axa fibrei, se gasesc in apropierea originii. In schimb, modurile LP_nm de ordin superior (cu n > 1) sunt foarte indepartate de origine. Modurile care se gasesc in afara acestei suprafete nu sunt ghidate, adica sunt foarte slabe. Modurile situate cu foarte putin in afara curbei limita sunt inca capabile sa se propage restrictiv, ele prezinta totusi o atenuare ridicata. Astfel de moduri sunt numite "moduri de fuga" fiind partial ghidate si partial degajate.

2.3. Profil segmentat (multitreapta)

Dispersia intr-o fibra monomod este o combinatie a doua tipuri de dispersie. Primul tip este dispersia materialului care rezulta dintr-o dependenta a indicelui de refractie de lungime de unda n=n(l)si astfel de viteza luminii c=c(l). Un al doilea tip de dispersie este dispersia ghidului de unda, care rezulta din dependenta repartitiei luminii modului fundamental LP₀₁ pe sticla miezului si invelisului (fig.1.65) rezultand diferenta relativa de indice D D l). Suma acestor doua dispersii se numeste dispersie cromatica.

In plaja lungimilor de unda superioare lui 1300 nm, cele doua tipuri de dispersie in sticla de cuart au semne opuse. Dispersia materialului nu poate fi modificata decat in limite restranse, variind dopajul sticlei de cuart. Din contra, dispersia ghidului de unda poate fi considerabil influentata variind structura profilului indicelui de refractie.

Profilul indicelui de refractie al unei fibre monomod obisnuita este un profil cu indice in treapta cu o diferenta relativa de indice D. Pentru acest profil simplu, suma dintre dispersia materialului si dispersia ghidului de unda este egala cu zero pentru o lungime de unda in jur de 1300 nm.

Daca vrem sa deplasam acest punct de zero al dispersiei catre alte valori ale lungimilor de unda, trebuie schimbata dispersia ghidului de unda si, in consecinta, schimbata structura profilului. Trebuie realizate profile segmentate sau cu multiple trepte de indice. Cu ajutorul acestor profiluri, este posibil sa se produca fibre optice in care dispersia nula sa fie decalata spre 1550 nm (fibre optice cu dispersie decalata) sau care au valorile de dispersie foarte slabe in gama de unde de 1300 si 1550 nm ( numite fibre optice cu dispersie compensata sau aplatizata).

In figura 1.70 dispersia cromatica M (l) este reprezentata in functie de lungimea de unda l pentru o fibra monomod fara decalaj al dispersie (1), cu decalaj al dispersiei (2) si cu dispersie compensata (3).

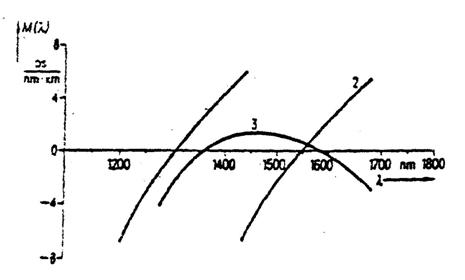
Fig. 1.70. Dispersia cromatica in functie de lungimea de unda.

1. Fara decalaj al dispersiei.

2. Cu decalaj al dispersiei

3. Cu aplatizare a dispersiei

Aceste fibre optice monomod pot fi realizate cu structuri de profil diferite. In cele ce urmeaza se prezinta o alegere a diverselor profil.

a)Tip 1 fara decalaj de dispersie

Profil cu indice in treapta simpla (simple step-index sau matched-cladding), figura 1.71.a.

Profil cu indice de refractie redus in invelis (depressed cladding), figura 1.71.b.

Fig. 1.71. Structuri de profil de fibre optice fara decalaj al dispersie

b)Tipul 2 cu decalaj al dispersiei

Profil segmentat cu miez triunghiular (segmentat core), figura 1.72.a.

Profil triunghiular (triunghiular profile), figura 1.72.b.

Profil segmentat cu indice in treapta dubla in invelis (double clad), figura 1.72.c.

Fig.1.72. Structuri de profil de fibre optice cu decalaj de dispersie.

c) Tipul 3 cu dispersie condensata

Profil segmentat cu indice in treapta cuadrupla in invelis, (quadruple clad), figura 1.73 a. Profil in forma de W (double clad), figura 1.73.b.

Fig.1.73. Structuri de profil in fibre optice cu aplatizarea dispersiei

3. PARAMETRII FIBREI OPTICE

Calitatea unui cablu cu fibra optica se verifica cu metode de masura diferite. In acest scop, o standardizare devine indispensabila pentru parametrii fibrei optice de masura si pentru metodele de masura respective. La nivel international, standardizarea este incredintata Comitetului Tehnic 86 al Comisiei Electrotehnice Internationale (CEI).

3.1. Atenuarea fibrei optice

Lumina care se propaga intr-o fibra optica, sufera o atenuare, adica are loc o pierdere de energie. Aceste pierderi trebuie sa ramana mici, pentru a putea parcurge distante mari, fara regeneratori intermediari. Atenuarea fibrei optice este un parametru important pentru efectuarea proiectarii instalarii cablurilor optice. Ea se datoreaza, in principal, fenomenelor fizice de absorbtie si difuzie.

Importanta acestor pierderi luminoase depinde, intre altele, de lungimea de unda a luminii injectate. Din aceasta cauza este, in general, util sa se masoare atenuarea fibrei optice in functie de unda (masura spectrala). Putem, astfel, determina gamele de unda cu pierderi mici, deosebit de interesante pentru transmisia optica.

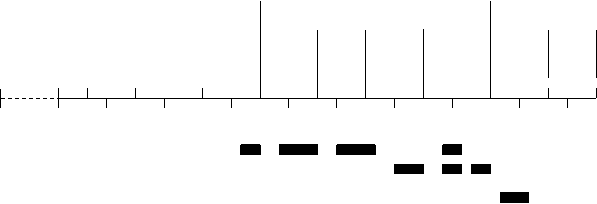
In timp ce fenomenul absorbtiei nu se produce decat la lungimi de unda precise, numite benzi de absorbtie (de exemplu 1390 nm: absorbtia OH), pierderile luminoase prin difuzie exista pentru toate lungimile de unda. Pentru ca difuzia rezulta din fluctuatiile densitatii (lipsa de omogenitate) in fibra optica si cum aceasta are dimensiuni adesea mai mici decat lungimea de unda a luminii, putem apela la legea de difuzie a lui Rayleigh care se enunta astfel: daca lungimea de unda l creste, pierderile prin difuzie a scad cu puterea a 4-a a lui l, (figura 1.74) , a l

Daca se compara, de exemplu, pierderile prin difuzie in lungimile de unda cele mai utile pentru comunicatii optice 850, 1300 si 1550 nm - putem observa ca la 1300 nm pierderile nu ating decat 18% din valoarea pe care o aveau la 850 nm (deci ele au in jurul lui 9% pentru 1550 nm). In concluzie, este avantajos sa se utilizeze cablurile cu fibra optica la aceste lungimi de unda.

Daca se observa propagarea luminii intr-o fibra optica in stare de echilibru, se poate constata ca puterea luminii P descreste exponential cu lungimea L a fibrei optice:

P (L) = P(o) ^lL/10

unde P(o) este egala cu puterea luminii injectate in fibra optica, P(L) este puterea luminii care se calculeaza la lungimea L iar a este coeficientul de atenuare, care este o masura pentru atenuarea pe unitatea de lungime. Atenuarea unei fibre optice de lungime L si cu un coeficient de atenuare a este:

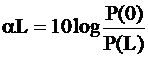
unde: a= coeficientul de atenuare, in dB/Km.

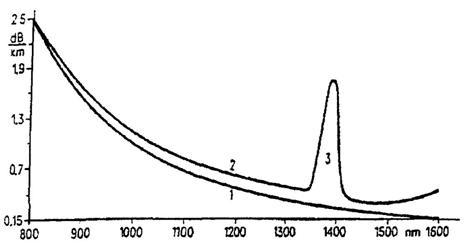
Fig. 1.74. Curba de atenuare a lui Rayleigh.

1. Atenuarea lui Rayleigh;

2. Atenuarea tipica a fibrei optice;

3. Absorbtia OH.

Aplicatie:

O atenuare de 10 dB inseamna ca puterea luminoasa P(L) masurata intr-o fibra optica dupa lungimea L (in Km), nu valoreaza mai mult de 10% din puterea luminoasa P(o) de intrare; pentru 3 dB se ating cifre de ordinul a 50% si pentru 1 dB in jur de 80%.

Fibrele monomod au, la o lungime de unda 1550 nm, atenuari de 0,2 dB/Km, adica doar 4,5% din puterea luminii se pierde pe kilometru. Curbele spectrale ale coeficientului de atenuare al unei fibre monomod si multimod tipice sunt prezentate in figura 1.75.

Pentru a determina coeficientul de atenuare al unei fibre optice, puterea luminii trebuie masurata in doua puncte distincte ale fibrei optice si cu conditia sa existe o stare de echilibru. Injectia luminii trebuie, deci, sa se efectueze in asa fel incat, pentru fibrele monomod sa nu mai fie moduri de invelis iar pentru fibrele multimod sa existe o stare de echilibru a modurilor intre cele doua puncte de masura. Din aceste motive se utilizeaza in general excitarea redusa la 70% pentru masurarea atenuarii.

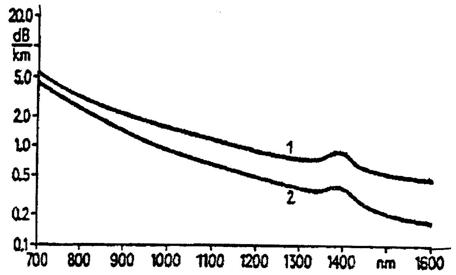
Fig.1.75. Curbele spectrale ale coeficientului de atenuare ale unei fibre optice mono si multimod:

1 fibra optica multimod; 2 fibra optica monomod.

3.2. Banda de trecere

Cei doi parametri mai importanti pentru definirea proprietatilor de transmisie ale unei fibre optice sunt atenuarea a si banda de trecere (bandwidth) B, de fapt in practica, produsul dintre largimea benzii si lungimea caracteristica egala cu b_1. In timp ce atenuarea descrie pierderile optice de linie ale fibrei optice, banda de trecere reprezinta o masura a fenomenului de dispersie.

Un impuls care se propaga in lungul unei fibre optice se imprastie in timp din cauza dispersiei. Din punct de vedere al frecventei, acest efect implica faptul ca fibra optica se comporta ca un filtru trece jos (low pass).

Aceasta inseamna ca odata cu cresterea frecventei de modulatie fm, se diminueaza amplitudinea undei luminoase in fibra pana la disparitia totala. Fibra optica lasa, deci, sa treaca semnale de frecvente mici si le atenueaza pe cele cu frecvente inalte. Daca se masoara, pentru fiecare frecventa de modulatie fm, amplitudinile puterii optice la intrarea in P₁(fm) si la iesirea P₂(fm) a fibrei optice si daca facem raportul lor, obtinem modulul frecventei de transfer (transfer function) H(fm):

H(fm) =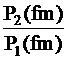

H(fm) este o functie de frecventa de modulatie fm. Obisnuit, se normeaza modulul functiei de transfer impartindu-l cu H(0), H(0) fiind functia de transfer pentru o frecventa de modulatie fm = 0, adica fara modulatie. Figura.1.76 descrie o curba tipica:

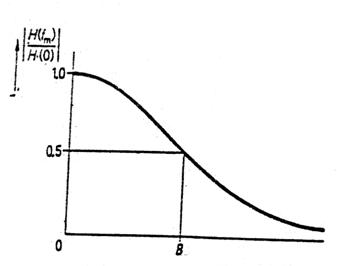
Fig.1.76. Functia de transfer a unei fibre optice

Caracteristica acestei curbe corespunde cu cea a unui filtru trece jos gaussian (gaussian low pass). Frecventa de modulatie pentru care valoarea normata a modului functiei de transfer este egala cu 0,5 este numita banda de trecere B a fibrei optice. Ea corespunde pentru:

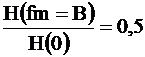
Banda de trecere este, deci, egala cu intervalul de frecventa in care amplitudinea (puterii optice) comparata cu valoarea sa la frecventa zero a scazut cu 50%, adica 3 dB.

3.3. Dispersia cromatica

Impulsurile luminoase se propaga in fibre optica cu o viteza de grup de:

c_g =

n_g fiind indicele de refractie de grup al sticlei miezului, care depinde de lungimea L, intr-un timp de grup:

t_g = .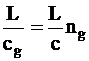

Deci, timpul de grup, depinde si de lungimea de unda. Fiecare sursa luminoasa pentru fibra optica, emite lumina sa nu numai pe o lungime de unda l unica, ci si intr-un spectru (largimea spectrala Dl distribuit in jurul acestei lungimi de unda. Datorita acestui lucru, cantitatile luminoase in Dl se propaga cu viteze diferite si aceasta implica diferiti timpi de intarziere. Dispersia materialului M₀ este o masura a variatiei indicelui de grup n_g pe diferite lungimi de unda. Ea este egala cu derivata indicelui de grup in raport cu lungimea de unda:

M₀.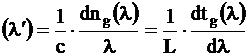

In ceea ce priveste unitatile de masura ale dispersiei se ia de obicei ps/nm Km.

Deoarece indicele de refractie de grup n_g al sticlei de cuart atinge un minim la o lungime de unda de circa 1300 nm, derivata se anuleaza in acest punct si dispersia materialului M₀ (l) este infinit de mica la aceasta lungime de unda. Valoarea dispersiei materialului depinde de materialul utilizat. Se poate, dopand in anumite conditii miezul, sa influenteze limitele dispersiei si astfel, punctul zero. Aceasta dispersie se produce in toate fibrele optice, fie ca ele sunt monomod sau multimod. In aceasta din urma, in apropierea punctului zero, dispersia modala intrece cu mult dispersia materialului. Exista si un alt efect de dispersie: dispersia ghidului de unda, cu o importanta deosebita pentru fibrele optice monomod. Ea se datoreaza faptului ca distributia luminii modului fundamental pe sticla miezului si a invelisului este o functie de lungime de unda.

In consecinta, aceasta dispersie este datorata diferentei relative de indice care depinde, de asemenea, de lungime de unda D D l

Cu lungimi de unda l crescatoare, modul fundamental LP₀₁ se extinde din materialul miezului in materialul invelisului (fig.1.77).

Aceasta implica, ca o cantitate crescatoare de lumina a modului fundamental este ghidata in invelisul care are indice de refractie mai scazut decat cel al miezului si, astfel, in plaja largimii spectrale Dl, exista diferente in timpii de intarziere. Viteza de propagare a undei luminoase este uniforma in miez si invelis, adica se formeaza o valoare medie ponderata a vitezelor in cele doua medii.

r r

l l < l

Fig. 1.77. Distributia energiei modului fundamental

in functie de doua lungimi de unda diferite

Suma celor doua tipuri de dispersie (dispersia materialului si dispersia ghidului de unda) este numita dispersia cromatica M (l

M (l) = M₀ (l) + M₁(l

Lungimea de unda l la care dispersia cromatica dispare, este numita lungime de unda la dispersia nula.

Figura 1.78. arata curbe de diferite dispersii ale unei fibre optice cu dispersie decalata si care se anuleaza la 1550 nm.

Amplitudinea radiala

normalizata a campului

1.00

0.75 V=1.5

V=2.0

0.50 V=3.0

1/e

0.25

r/a

0 0.50 1.00 1.50 2.00 2.50 3.00 3.50 4.00

Fig.1.78. Curbe de dispersie ale unei fibre optice monomod

Un impuls luminos injectat intr-o fibra optica monomod, de o sursa de largime spectrala Dl (largime la jumatatea inaltimii maximului) care corespunde unei largimi spectrale efective Dl_ef ce variaza in timp datorita dispersiei cromatice M(l

Lungimea impulsului este proportionala cu lungimea L a fibrei optice si cu largimea spectrala Dl a sursei.

Valori tipice pentru dioda laser (DL) sunt Dl=3-5 nm iar pentru dioda electroluminiscenta Dl=40-70 nm (la 850 nm).

Aceasta formula este valabila pentru impulsuri si spectre gaussiene, cu conditia ca lungimea de unda medie l_m a sursei sa nu fie in apropierea lungimii de unda l unde dispersia cromatica M(l) este nula.

Banda de trecere B a unei fibre monomod se poate calcula in functie de lungimea de unda l pentru un spectru de emisie gaussian si o lungime efectiva a impulsurilor T_ef:

B =.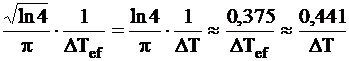

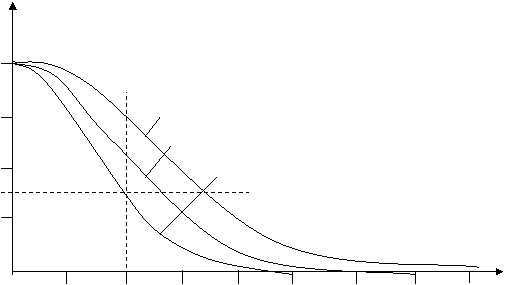
Figura 1.79. arata curbele benzii de trecere pentru o fibra optica monomod tipica, in functie de diferitele largimi spectrale Dl

Produsul largimii de banda

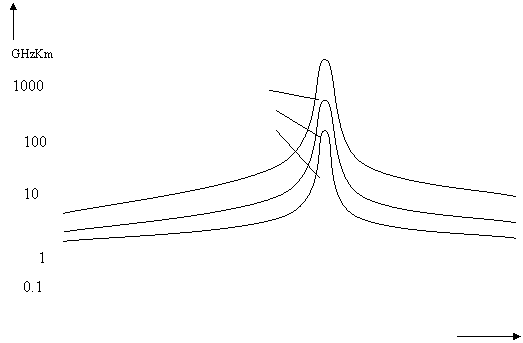Lungime caracteristica

10000

1000 1100 1200 1300 1400 1500 nm 1600

l

Fig. 1.79. Produsul largime de banda - lungime caracteristica a unei fibre optice monomod, in functie de largimea spectrala Dl a sursei.

3.4. Lungimea de unda de taiere

Intr-o fibra optica se propaga unul sau mai multe moduri potrivit cu lungimea de unda. Este important pentru buna functionare sa se determine lungimea de unda corespunzatoare astfel incat fibra optica respectiva sa ghideze doar modul fundamental LP₀₁. Lungimea de unda de taiere (cutt-off-wavelength) a unei fibre desemneaza cea mai joasa lungime de unda de functionare de la care se propaga doar modul fundamental. Deasupra acestei lungimi de unda de taiere l_c, modul urmator adica LP₁₁ dispare.

Pentru valori ale lungimii de unda mai mici decat lungimea de unda de taiere se obtin diferite moduri. Fibra optica este, deci, multimodala pentru lungimi de unda inferioare lui l_c si monomodala pentru lungimi de unda superioare lui l_c

3.5. Diametrul campului de mod

Distributia luminoasa a modului fundamental intr-o fibra monomod joaca un rol important in evaluarea pierderilor de injectie, de curbura sau datorate imbinarilor. Raza campului de mod W₀ sau diametrul campului de mod 2W₀ au fost definite pentru a descrie aceasta distributie (fig. 1.80).

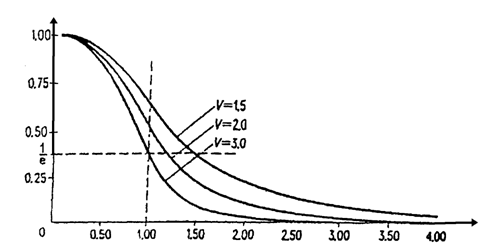
Fig. 1.80. Dependenta radiala a amplitudinii campului de modul fundamental.

Raza campului de mod W₀ este egala cu raza pentru care amplitudinea radiala a campului s-a micsorat la 1/e (~37 %) din maxima langa axa fibrei (r = 0).

Diametrul campului de mod 2W₀ depinde de lungimea de unda, el se mareste la lungimi de unda crescatoare. Raza campului de mod W₀ raportata la raza miezului (fig.1.80.) nu este decat o functie de frecventa normalizata, care depinde de lungimea de unda l si de deschiderea numerica AN:

V =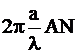

Pentru fibra monomod, avand o frecventa normalizata

1,6 < V > 2,6 exista o formula care descrie, cu o destul de buna aproximare, relatia dintre raza campului W₀ , raza miezului a si frecventa normalizata V:

W₀ =

Gama de frecvente normalizate citata mai sus corespunde unei game de unde de la 1150 nm la 1875 nm si acopera astfel, lungimile de unda de functionare de 1300 nm si 1550 nm.

3.6. Camp apropiat si dimensiuni geometrice

Campul apropiat al unei fibre optice (near field distribution) corespunde repartitiei de densitate a puterii optice pe suprafata sectiunii transversale la capatul acestei fibre.

3.7. Camp indepartat

Campul indepartat al unei fibre optice (far field distribution) corespunde repartitiei puterii optice I_f (q) radiata la capatul fibrei, in functie de unghiul q q fiind unghiul format de raza luminoasa si axa optica a fibrei.