Influenta temperaturii asupra echilibrului chimic

Influenta temperaturii asupra echilibrului chimic

Conform principiului lui Le Chatelier, cresterea de temperatura va favoriza deplasarea echilibrului in sensul reactiei endoterme si scaderea temperaturii va actiona favorabil asupra reactiei exoterme.

Exemplu:

2NO + O₂ Û 2NO₂ H < 0

Reactia este favorizata de scaderea temperaturii (à deplasarea echilibrului) deoarece este exoterma ( H < 0).

Relatia care exprima legatura dintre constanta de echilibru si variatia de temperatura se obtine, pornind de la expresia entalpiei libere standard (6.12). Pentru a urmari deplasarea echilibrului chimic cu temperatura, se inlocuieste entalpia libera standard (relatia 6.12) in ecuatia lui Gibbs-Helmholtz (4.183):

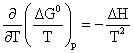
obtinandu-se:

(6.26)

Ecuatia (6.26) se numeste izobara de reactie a lui van't Hoff. Analizand aceasta ecuatie se constata o concordanta perfecta cu principiul lui Le Chatelier. Daca reactia este endoterma ( H > 0), constanta de echilibru creste cu cresterea temperaturii, cu deplasarea echilibrului inspre formarea produsilor de reactie. Daca reactia este exoterma ( H < 0), constanta de echilibru scade cu cresterea temperaturii.

Scriind ecuatia lui van't Hoff (6.26) sub forma:

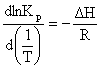(6.27)

se observa ca reprezentarea grafica a lui lnK_p in functie de 1/T duce la o curba a carei panta este egala cu - H/R. Daca H se mentine constanta in intervalul de temperatura ales, curba devine o dreapta (fig. 6.1.).

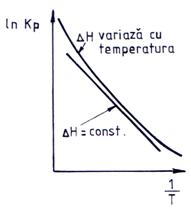
Fig. 6.1. Variatia lui lnK_p in functie de 1/T

Pentru a fi utila in calcule termodinamice, ecuatia lui van't Hoff (6.26) trebuie integrata. Integrarea se face intre doua limite de temperatura T₁ si T₂ sau in mod nedefinit. Integrand intre T₁ si T₂ si considerand ca H este constant, se obtine:

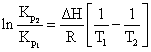(6.28)

unde:      = constanta de echilibru corespunzatoare temperaturii T₁, respectiv T₂.

Daca integrarea ecuatiei lui van't Hoff (6.26) se face in mod nedefinit rezulta:

(6.29)

daca H = const.

Constanta de integrare din ecuatia (6.29) se poate determina daca se cunoaste valoarea constantei K_p la o temperatura data.

Daca H variaza cu temperatura, se face apel la legea lui Kirchhoff (4.98) pentru a exprima variatia entalpiei de reactie a carei substituire in ecuatia lui van't Hoff (6.26) duce la egalitatea:

(6.30)

Integrand ecuatia (6.30) intre limitele T₁ si T₂ se obtine:

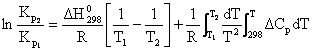(6.31)

unde:      = entalpia de reactie la 298 K;

C_p se inlocuieste cu relatia (4.100).

In cazul reactiilor care au loc la volum constant, este mai potrivit sa se foloseasca K_c in loc de K_p.

Din ecuatia (6.19) rezulta prin logaritmare:

(6.32)

Derivand relatia (6.32) in raport cu temperatura, se obtine:

(6.33)

Inlocuind relatia (6.33) in ecuatia izobarei (6.26) rezulta:

(6.34)

respectiv

(6.35)

Stiind ca la presiune constanta, exista relatia (4.69):

ΔU = H - p V = H - nRT

ecuatia (6.35) devine:

(6.36)

Ecuatia (6.36) se numeste izocora de reactie a lui van't Hoff.