| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
1. DIFEOMORFISME DE CLASA C1
Fie U si V doua multimi deschise din Rn.
Definitia 1.1 (difeomorfism)
O functie ![]() se numeste difeomorfism de
se numeste difeomorfism de
clasa C1 (C1- difeomorfism) de la U la V, daca:
f este bijectiva
f este de clasa C1 pe U
f -1 este de clasa C1 pe V.
Observatia 1.2
a) Inversul unui C1-difeomorfism este C1-difeomorfism.
b) Compunerea a doua C1-difeomorfisme este C1-difeomorfism.
Propozitia 1.3
Daca f: U V este un C1-difeomorfism atunci pentru orice x U are loc relatia
![]() , unde y =f(x
, unde y =f(x
Demonstratie:
Cum prin ipoteza, f si f-1 sunt functii continue,
diferentiabile iar![]() folosind teorema de diferentiere a functiilor compune, pentru
folosind teorema de diferentiere a functiilor compune, pentru ![]() , daca y = f(x ),
avem:
, daca y = f(x ),
avem:
![]()
![]()
de
unde ![]() .
.
Teorema 1.4
Fie f:U V un homeomorfism.
Daca f este diferentiabila in x0
I U si ![]() este inversabila, atunci f -1este
diferentiabila in y0 = f(x0).
este inversabila, atunci f -1este
diferentiabila in y0 = f(x0).
Demonstratie:
Cum prin ipoteza, f este bijectiva, pentru k I Rn cu proprietatea ca y0 + k = f(x0 + h) si anume h =f -1(y0+k) - f -1(y0).
Daca f este diferentiabila in x0 I U, atunci din egalitatea y0 + k = f(x0 + h) obtinem:
![]() (1)
(1)
unde![]() .
.
Pe de alta parte, ![]() fiind inversabila, avem:
fiind inversabila, avem:
![]()
si atunci
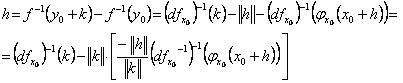
pentru
![]() i. y0 + kI V.
i. y0 + kI V.
Daca k Rn, atunci, din continuitatea functiei f-1 rezulta ca h 0Rn si deci, deoarece
![]() atunci:
atunci:
![]()
Vom arata ca raportul ![]() este marginit pe o vecinatate a originii .
este marginit pe o vecinatate a originii .
Din egalitatea (1) rezulta:
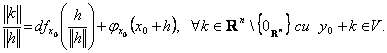
Cum ![]() apartine sferei unitate
apartine sferei unitate 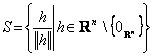 care fiind marginita si inchisa din Rn, iar aplicatia
care fiind marginita si inchisa din Rn, iar aplicatia
![]()
fiind continua avem:
![]() .
.
Cum aIS este nenul si ![]() este inversabila, rezulta ca
este inversabila, rezulta ca
![]()
Pentru ![]() suficient de mic avem:
suficient de mic avem: ![]() ,
de unde
,
de unde
![]()
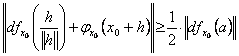 .
.
Functia f-1 fiind
continua, pentru ![]() suficient de mic, obtinem:
suficient de mic, obtinem:
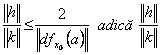 este marginit.
este marginit.
Prin urmare
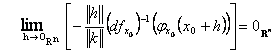
deci f-1 este diferentiabila in y0.
Vom accepta fara demonstratie urmatoarea teorema:
Teorema 1.5
Fie f:U V un homeomorfism.
Daca f este C1 pe U si dfx este inversabila pentru xIU, atunci f-1este de clasa C1 pe V (adica f-1 este C1-difeomorfism).
Teorema 1.6 (de inversiune locala)
Fie A Ì Rn o multime deschisa si x0 I A
Daca f: AÌRn Rn este o functie de clasa C1 pe A
si ![]() este inversabila, atunci UÌA deschisa si V I Rn deschisa a.i.
functia h: U V, definita prin h(x) = f(x), este C1-difeomorfism.
este inversabila, atunci UÌA deschisa si V I Rn deschisa a.i.
functia h: U V, definita prin h(x) = f(x), este C1-difeomorfism.
Demonstratie:
Consideram aplicatiile:
![]() ,
unde notam
,
unde notam
A1 = j(A), B1=Y(f(A)). Functiile j si Y sunt difeomorfisme. Consideram functia f :A1 B1 f1 Y f j
Observam ca ![]()
Se arata usor ca functia f este diferentiabila in x0 Û f este diferentiabila in 0.
Aceasta ne permite sa fie suficient sa demonstram teorema pentru functii
f: AIRn Rn de clasa C1 pe A cu 0I A, f(0) =0 si df0 inversabila.
![]() .
.
Conform teoremei de diferentiabilitate a functiilor compuse F este diferentiabila in 0 si
![]()
Fie g: AÌ Rn Rn g = F - 1Rn
Aplicatia g este diferentiabila in 0 si dg0 = dF0 - 1Rn = 0 (aplicatia liniara identic nula).
Cum gI C1(A), aplicatia diferentiala dg :A L(Rn, Rn) este continua pe A, deci d > a.i. pentru xI A, cu x < d are loc
![]() .
.
Conform teoremei de medie, pentru orice x,x1ID (0,d rezulta:
![]() (2)
(2)
In particular, pentru x = 0, din egalitatea (2) obtinem xID(0,d
![]() (3)
(3)
Fie: ![]() .
.
Evident V este deschisa si din continuitatea lui F rezulta ca U este deschisa, iar
![]()
Consideram ![]() fixat.
fixat.
Definim aplicatia ![]() prin:
prin:
![]()
Atunci pentru ![]()
![]()
Pe de alta parte, x1, x2 I D(0,d
![]()
deci
jy este o ![]() -
contractie.
-
contractie.
Conform principiului contractiei, j are un unic punct fix x*ID(0,d jy(x*) = x*.
Dar jy(x*) = x* Û y = F(x*) si prin urmare, aplicatia H:U V' definita prin H(x) = F(x) este o bijectie. Atunci
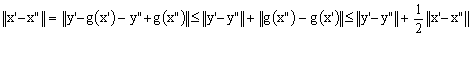
si
de aici ![]() .
.
Prin urmare, pentru y',y''IV', ![]() deci H-1 fiind lipschitziana, este
continua.
deci H-1 fiind lipschitziana, este
continua.
Din cele prezentate mai sus rezulta ca aplicatia H:U V' este un homeomorfism.
Deoarece dF(0) = 1Rn rezulta ca matricea JF(0) este nesingulara, adica det JF(0) ¹
Cum FIC1(A), elementele matricii JF sunt functii continue pe A si prin urmare aplicatia
x: A det JF(x) I R este continua pe A.
Atunci, UIV(0), UÌU a.i. det JF(x) ¹ xIU, deci dFx este inversabila, xIU.
Daca luam V = H(U), atunci V este o multime deschisa.
Fie H U restrictia lui H la multimea U.
Deoarece H U:U V este un homeomorfism de clasa C1 pe U si pentru x IU, dHx = dFx este inversabila, rezulta ca H U este C1-difeomorfism.
Fie h:U V, h(x) = f(x). Atunci din H U = (df0) o h rezulta h = df0 o H U si deci h este C1 -difeomorfism.
Aplicatie (Schimbari de variabile)
Fie U, V doua multimi deschise din Rn si
f: (x1, x2, ., xn) I U Ì Rn y = f(x1, x2, ., xn) IR o functie de clasa Ck, k³1, pe multimea U.
Presupunem ca aplicatia j : V U
j: (u1, u2,., un) (x1, x2, ., xn) = (j (u1, u2,., un)),., jn(u1,.,un))
este un difeomorfism de clasa Ck de la V pe U.
Se stie ca atunci functia g : V R, g = f o j, este de clasa Ck pe V. Ne propunem sa calculam derivatele partiale ale lui g.
In cazul ca putem explicita pe j , atunci pentru calculul derivatelor partiale punem
Y j Y Y Yn) si ne folosim de formula
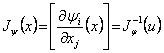
unde x = (x1, x2,., xn), u = (u1, u2, .,un).
Folosind formula de derivare a functiei compuse f = g o j avem
![]() , unde u = y(x).
, unde u = y(x).
In cazul cand nu putem explicita pe j , atunci din relatia matriciala Jg(u) = Jf(x)Jj(u) unde x = j(u) se obtine sistemul Cramer
![]() in necunoscutele
in necunoscutele ![]() (determinantul
(determinantul
sistemului
este jacobianul lui j in u). Prin rezolvarea sistemului se
obtin ![]() in functie de
in functie de
![]()
Teorema 1.7 (a functiei implicite)
Fie o functie de clasa C1 pe multimea deschisa A:
![]()
Daca (xo, yo) I A, astfel incat
f(xo, yo) = 0Rp
![]()
atunci
a)
![]()
b)
![]() , astfel incat yo = g(xo) si f(x, g(x)) = 0Rp , xIU.
, astfel incat yo = g(xo) si f(x, g(x)) = 0Rp , xIU.
c)
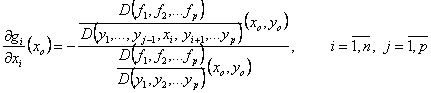
Demonstratie:
Fie h: A Ì Rn Rp Rn Rp definita prin, h(x,y) = (x, f(x, y)). Atunci
![]() si acesta este nenul conform
ipotezei 2).
si acesta este nenul conform
ipotezei 2).
In plus, h este de clasa C1 pe A.
In baza Teoremei de inversiune locala, ![]() si
o vecinatate
si
o vecinatate
deschisa
V* a lui h(xo,yo) = (xo, f(xo, yo))
= (xo, 0Rp), V* = h(U*), astfel incit functia j:U* V*, definita prin ![]() este un C1 -difeomorfism.
este un C1 -difeomorfism.
Multimea U* poate fi aleasa de forma U* = U V, unde U este o multime deschisa din Rn cu xoI U, iar V este o multime deschisa din Rp, cu yoIV.
Asadar, j:U V V* este un C1 -difeomorfism, iar inversul sau j : V* U V este de forma j (x,y) = (x, Y(x,y)), unde Y:UxV Rp este de clasa C1 pe UxV.
Fie p:U V Rp, definita prin p(x,y) = y.Atunci p o j = f si
![]() deci f(x,y(x,0Rp)) = 0Rp.
deci f(x,y(x,0Rp)) = 0Rp.
Aplicatia cautata este g:U V, g = (g1,., gp) definita prin g(x) = y(x, 0Rp).
Unicitatea lui g rezulta din unicitatea lui y
Pentru a deduce formula de derivare de la punctul c) observam ca pentru x I U
![]()
![]()
sau
![]()
Sistemul (4) este liniar si neomogen, cu p ecuatii si p necunoscute. Cum prin ipoteza, determinantul sistemului (4)
![]()
este nenul, sistemul are solutie unica si prin rezolvarea lui cu regula lui Cramer se obtine formula c
In continuare, in ipotezele Teoremei 4.4, vom considera urmatoarele cazuri particulare:
I.
Cazul n = p = 1: Functia f:AÌ R R R, (x,y) f(x,y) se anuleaza in punctul (x0,y0) I A, adica f(x0,y0) = 0 si ![]() .
.
Atunci ![]()
![]() astfel
incat:
astfel
incat:
![]() , gIC1(U) pentru care f(x, g(x)) = 0, xIU si
, gIC1(U) pentru care f(x, g(x)) = 0, xIU si 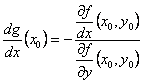 .
.
II. Cazul n ¹ 1, p =1: Functia f: A Ì Rn R R, unde x = (x1, x2, ., xn) se anuleaza
in
punctul (x0, y0) IA, adica f(x0,
y0) = 0 si ![]() .
.
Atunci, o vecinatate U a punctului x0 = (a1,a2,., an), U Ì Rn, o vecinatate deschisa V a punctului y0, VÌ R si o unica functie g : U V, de clasa C1 pe U astfel F(x, g(x)) = 0, x I U si

III. Cazul n = 1, p ³ 2: Fie f: A Ì R Rp Rp, f = (f1, f2, ., fp), unde x I R, y = (y1, y2, ., yp) I Rp.
Ecuatia f(x,y) = 0Rp este echivalenta cu sistemul

Daca pentru (x0,
y0) I A, f(x0, y0) = 0Rp si ![]() atunci exista o vecinatate deschisa U Ì R, a lui x0, o
vecinatate deschisa VÌ Rp, a lui y0 si o unica functie g: U V, g = (g1, ., gp) de
clasa C1 pe U astfel incat
atunci exista o vecinatate deschisa U Ì R, a lui x0, o
vecinatate deschisa VÌ Rp, a lui y0 si o unica functie g: U V, g = (g1, ., gp) de
clasa C1 pe U astfel incat ![]()
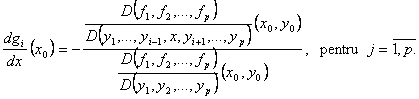
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1766
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved