| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Probleme propuse pentru Concursul de matematica "Adolf Haimovici"
Probleme propuse pentru clasa a IX-a
1. Fie ![]() functia care satisface conditiile:
functia care satisface conditiile:
a) ![]() ,
,
b) ![]() ,
,
c) ![]() pentru
orice
pentru
orice ![]() ,
,
![]() fiind o
fiind o
Se cere:
1) Sa se afle valoarea lui ![]() ;
;
2) Sa se determine ![]() si
si ![]() ;
;
3) Sa se gaseasca expresia functiei ![]() ;
;
4) Sa se calculeze![]() ;
;
5) Sa se rezolve ecuatia 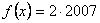 .
.
Rezolvare. 1) Pentru ![]() si
si ![]() din relatia de la c) obtinem
din relatia de la c) obtinem ![]() , de unde rezulta
, de unde rezulta ![]() .
.
2) Pentru ![]() si
si ![]() ,
,
![]() din relatia de la c) obtinem
din relatia de la c) obtinem ![]() ,
de unde
,
de unde ![]() iar pentru
iar pentru ![]() ,
,
![]() ,
, ![]() ,
de unde
,
de unde ![]() .
.
3) Pentru ![]() si
si ![]() din relatia de la c) obtinem
din relatia de la c) obtinem ![]() . Inlocuind pe
. Inlocuind pe ![]() cu
cu ![]() gasim
gasim ![]() pentru orice
pentru orice![]() .
.
4) ![]() .
.
5) Ecuatia a carei rezolvare se cere este ![]()
care are
solutiile ![]() si
si ![]() .
.
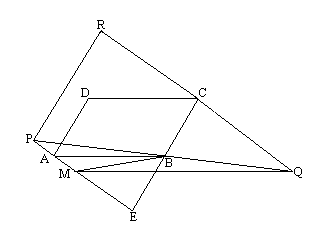
2. In planul paralelogramului ![]() se considera
se considera ![]() simetricul lui
simetricul lui ![]() fata de
fata de ![]() si
si ![]() un punct pe segmentul
un punct pe segmentul ![]() astfel incat
astfel incat ![]() .
Fie
.
Fie ![]() simetricul lui
simetricul lui ![]() fata de
fata de ![]() ,
,
![]() simetricul lui
simetricul lui ![]() fata de
fata de ![]() si
si ![]() simetricul lui
simetricul lui ![]() fata de
fata de ![]() .
.
a) Sa se gaseasca descompunerile vectorilor ![]() si
si ![]() dupa directiile vectorilor
dupa directiile vectorilor ![]() .
.
b) Sa se arate ca patrulaterul ![]() este trapez si sa se afle raportul bazelor.
este trapez si sa se afle raportul bazelor.
c) Sa se arate ca punctele ![]() sunt coliniare.
sunt coliniare.
Rezolvare. a) Vectorii ![]() si
si ![]() se pot
exprima dupa cum urmeaza.
se pot
exprima dupa cum urmeaza.
![]()
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
b) Din relatiile (1), (2) avem ![]() ,
ceea ce inseamna ca vectorii
,
ceea ce inseamna ca vectorii ![]() si
si ![]() sunt coliniari. Rezulta ca patrulaterul
sunt coliniari. Rezulta ca patrulaterul ![]() este trapez si raportul bazelor este
este trapez si raportul bazelor este ![]() .
.
c) Exprimam vectorii ![]() si
si ![]() in functie de
in functie de ![]() :
:
![]() ,
,
![]() .
.
Se vede ca
vectorii ![]() si
si ![]() sunt coliniari si in consecinta punctele
sunt coliniari si in consecinta punctele ![]() sunt coliniare.
sunt coliniare.
Probleme propuse pentru clasa a X-a:
1. Fie ![]() functia care satisface conditiile:
functia care satisface conditiile:
a) ![]() ,
,
b) ![]() ,
,
c) ![]() pentru
orice
pentru
orice ![]() ,
,
![]() fiind o
fiind o
Se cere:
1) Sa se afle valoarea lui ![]() ;
;
2) Sa se determine ![]() si
si ![]() ;
;
3) Sa se gaseasca expresia functiei ![]() ;
;
4) Sa se arate ca ![]() pentru orice
pentru orice ![]() ;
;
5) Sa se rezolve ecuatia ![]() .
.
Rezolvare. Relatia de la c) se mai poate scrie
(1) ![]()
1) Pentru ![]() din relatia (1) obtinem
din relatia (1) obtinem ![]() , de unde rezulta
, de unde rezulta ![]() .
.
2) Pentru ![]() si
si ![]() ,
,
![]() din relatia (1) obtinem
din relatia (1) obtinem ![]() , iar pentru
, iar pentru ![]() ,
,
![]() ,
, ![]() ,
de unde
,
de unde ![]() .
.
3) Pentru ![]() si
si ![]() din relatia (1) obtinem
din relatia (1) obtinem ![]() . Inlocuind pe
. Inlocuind pe ![]() cu
cu ![]() gasim
gasim ![]() pentru orice
pentru orice![]() .
.
4) ![]() .
.
5) Ecuatia se scrie succesiv
![]()
![]()
![]()
care are
solutiile ![]() si
si ![]() .
.
2. Stiind ca ![]() se cer:
se cer:
a) Sa se arate ca ![]() , unde
, unde ![]() ;
;
b) Sa se arate ca ![]() pentru orice
pentru orice ![]() ;
;
c) Sa se stabileasca semnele
numerelor ![]() si
si ![]() ;
;
d) Sa se compare numerele ![]() si
si ![]() ;
;
e) Sa se arate ca ![]() .
.
Rezolvare: a) Avem
![]()
![]()
de unde rezulta relatia de la a).
b) Reprezentand unghiul cu masura ![]() pe cercul trigonometric, aria tringhiului AOM este egala cu
pe cercul trigonometric, aria tringhiului AOM este egala cu ![]() iar a sectorului de cerc AOM este egala cu
iar a sectorului de cerc AOM este egala cu ![]() .
.
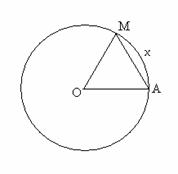
Rezulta ![]() .
.
c) Utilizand rezultatul de la a) avem
![]()
![]()
d) Folosim urmatoarele inegalitati
sin(cos x) <
cos(sin x) pentru orice x![]() ,
,
(2) sin(sin x) < cos(cos x) pentru orice x![]() ,
,
care se obtin pe
baza monotoniei functiilor ![]() si
si ![]() si a inegalitatii de la b)
si a inegalitatii de la b)
dupa cum urmeaza :
sin(cos x) < cos x < cos(sin x),
sin(sin x) =
sin(cos(![]() -
x)) < cos(sin(
-
x)) < cos(sin(![]() -
x)) = cos(cos x).
-
x)) = cos(cos x).
Atunci
![]()
![]() .
.
e) Pe baza inegalitatilor (1), (2) obtinem
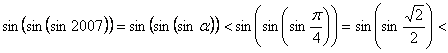
 .
.
Probleme propuse pentru clasa a XI-a
1. Fie ![]() functia care satisface conditiile:
functia care satisface conditiile:
a) ![]() ,
,
b) ![]() ,
,
c) ![]() pentru orice
pentru orice ![]() ,
,
![]() fiind o
fiind o
Se cere:
1) Sa se afle valoarea lui ![]() ;
;
2) Sa se determine ![]() ;
;
3) Sa se calculeze ![]() ;
;
4) Sa se gaseasca expresia functiei ![]() .
.
Rezolvare. 1) Pentru ![]() din relatia de la c) obtinem
din relatia de la c) obtinem ![]() , de unde rezulta
, de unde rezulta ![]() .
.
2) Pentru ![]() si
si ![]() din relatia de la c) obtinem
din relatia de la c) obtinem ![]() , de unde
, de unde ![]() .
.
3) ![]()
![]() .
.
4) Pentru ![]() si
si ![]() din relatia de la c) obtinem
din relatia de la c) obtinem ![]() , adica
, adica ![]() .
Inlocuind pe
.
Inlocuind pe ![]() cu
cu ![]() gasim
gasim ![]() pentru orice
pentru orice ![]() .
.
2. Fie M = .
.
a) Cate elemente are multimea M ?
b) Cate matrice din multimea M sunt inversabile?
c) Daca ![]() M este o matrice inversabila sa se determine inversa ei..
M este o matrice inversabila sa se determine inversa ei..
d) Care este matricea din multimea M al carei determinant are valoarea cea mai mare?
e) Care este matricea din multimea M al carei determinant are valoarea cea mai mica?
Rezolvare: a) Fiecare dintre
parametrii ![]() poate lua 2 valori si astfel multimea M are 8 elemente.
poate lua 2 valori si astfel multimea M are 8 elemente.
b) Daca ![]() M , atunci
M , atunci
![]() .
.
Cum pentru ![]() si
si ![]() avem
avem ![]() rezulta ca multimea M are 4 matrice inversabile.
rezulta ca multimea M are 4 matrice inversabile.
c) Daca ![]() M este o matrice inversabila, avem
M este o matrice inversabila, avem ![]() ,
,
 ,
, 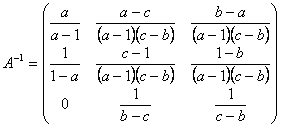 .
.
d) Cea mai mare valoare a lui ![]() se obtine pentru
se obtine pentru
![]() .
.
e) Cea
mai mica valoare a lui ![]() se obtine pentru
se obtine pentru
![]() .
.
Probleme propuse pentru clasa a XII-a:
1.
Pe multimea ![]() se considera legea de compozitie "
se considera legea de compozitie " ![]() " definita prin relatia
" definita prin relatia ![]() , unde
, unde ![]() semnifica partea intreaga.
semnifica partea intreaga.
a) Sa se arate ca
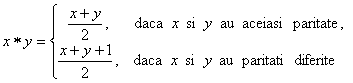
pentru orice ![]() .
.
b) Sa se intocmeasca tabla legii
de compozitie " ![]() " pe
multimea
" pe
multimea ![]() .
.
c) Sa se stabileasca daca legea de compozitie " ![]() " admite element neutru pe multimea
" admite element neutru pe multimea ![]() .
.
d) Sa se stabileasca daca legea de compozitie " ![]() " este
comutativa.
" este
comutativa.
e) Sa se arate ca legea de compozitie " ![]() " nu
este asociativa.
" nu
este asociativa.
f) Sa se rezolve in multimea ![]() ecuatia
ecuatia ![]() .
.
Rezolvare: a) Daca ![]() si
si ![]() au aceiasi paritate atunci
au aceiasi paritate atunci ![]() este numar par si
este numar par si ![]() .
Prin calcul gasim
.
Prin calcul gasim ![]() Daca
Daca ![]() si
si ![]() au paritati diferite atunci
au paritati diferite atunci ![]() este numar impar si
este numar impar si ![]() .
Prin calcul gasim
.
Prin calcul gasim ![]()
b) Tabla legii de compozitie este
|
* |
0 |
1 |
2 |
3 |
|
0 |
0 |
1 |
1 |
2 |
|
1 |
1 |
1 |
2 |
2 |
|
2 |
1 |
2 |
2 |
3 |
|
3 |
2 |
2 |
3 |
3 |
c) Din tabla legii de compozitie se vede ca aceasta nu admite element neutru.
d) Tabla legii de compozitie este simetrica fata de diagonala principala ceea ce inseamna ca legea " * " este comutativa.
c) Pentru elementele ![]() avem
avem
![]() si
si ![]()
ceea ce arata ca legea " * " este nu este asociativa.
d) Din tabla legii de compozitie se vede ca ecuatia ![]() are solutiile
are solutiile ![]() .
.
2. Se considera functia continua 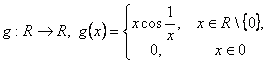 si fie
si fie
![]() o primitiva a lui
o primitiva a lui ![]() . Definim functia
. Definim functia

a) Sa se arate ca functia ![]() este contina pe
este contina pe ![]() .
.
b) Sa se arate ca functia ![]() este derivabila pe
este derivabila pe ![]() .
.
c) Sa se arate ca ![]() este o primitiva a functiei
este o primitiva a functiei
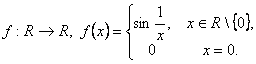
Rezolvare: a) Functia ![]() fiind o primitiva a lui
fiind o primitiva a lui ![]() este
contina pe
este
contina pe ![]() .
In baza operatiilor cu functii continue rezulta ca
.
In baza operatiilor cu functii continue rezulta ca ![]() este contina pe
este contina pe ![]() .
In 0 avem
.
In 0 avem ![]() ceea ce inseamna ca
ceea ce inseamna ca ![]() este contina in 0. In consecinta
este contina in 0. In consecinta ![]() este contina pe
este contina pe ![]() .
.
b) Functia ![]() fiind o primitiva a lui
fiind o primitiva a lui ![]() este
derivabila pe
este
derivabila pe ![]() .
Mai departe, pentru
.
Mai departe, pentru ![]() avem
avem
![]()
iar
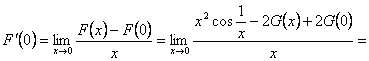
![]() .
.
In consecinta ![]() este derivabila pe
este derivabila pe ![]() .
.
c) De la b) se vede ca ![]() ceea ce inseamna ca
ceea ce inseamna ca ![]() este o primitiva a functiei
este o primitiva a functiei ![]() .
.
3. Fie ![]() functia care satisface conditiile:
functia care satisface conditiile:
a) ![]() ,
,
b) ![]() ,
,
c) ![]() pentru orice
pentru orice ![]() ,
,
![]() fiind o
fiind o
Se cere:
1) Sa se afle valoarea lui ![]() ;
;
2) Sa se determine ![]() si
si ![]() ;
;
3) Sa se gaseasca ![]() pentru orice
pentru orice ![]() ;
;
4) Sa se gaseasca expresia functiei ![]() .
.
Rezolvare. 1) Pentru ![]() din relatia de la c) obtinem
din relatia de la c) obtinem ![]() , de unde rezulta
, de unde rezulta ![]() .
.
2) Pentru ![]() si
si ![]() din
relatia de la c) obtinem
din
relatia de la c) obtinem ![]() , de unde
, de unde
![]()
Din definitia derivatei intr-un punct avem
![]()
3) Intr-un punct oarecare ![]() avem
avem
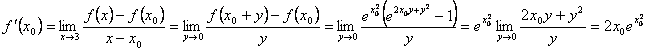 si deci
si deci ![]() pentru orice
pentru orice ![]() .
.
4) Functia ![]() este primitive lui
este primitive lui ![]() care in 1 ia valoarea
care in 1 ia valoarea ![]() .
Se obtine
.
Se obtine ![]() pentru orice
pentru orice
![]() .
.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2082
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved