| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Diferentiabilitatea functiilor de mai multe variabile
Fie ![]() o functie de doua variabile definita pe o
multime
o functie de doua variabile definita pe o
multime ![]() si
si ![]() un punct interior al lui
un punct interior al lui ![]() .
.
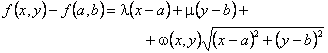
Daca ![]() este o multime deschisa se spune ca
este o multime deschisa se spune ca ![]() este diferentiabila pe
este diferentiabila pe ![]() daca este diferentiabila in orice punct din
daca este diferentiabila in orice punct din ![]() .
.
Se va nota ![]() , deci
egalitatea de mai sus se scrie
, deci
egalitatea de mai sus se scrie
![]()
unde ![]() .
.
Lema 1. Daca functia ![]() definita pe
definita pe ![]() , are
limita 0 in
, are
limita 0 in ![]() , atunci
exista doua functii
, atunci
exista doua functii ![]() si
si ![]() definite pe
definite pe ![]() care au limita 0 in
care au limita 0 in ![]() si
si
![]() ,
, ![]() .
.
Reciproc, daca functiile ![]() si
si ![]() definite pe
definite pe ![]() , au limita
0 in punctul
, au limita
0 in punctul ![]() atunci exista o functie
atunci exista o functie ![]() cu limita 0 in
cu limita 0 in ![]() care sa verifice egalitatea precedenta.
care sa verifice egalitatea precedenta.
Folosind aceasta lema, rezulta imediat:
Propozitia 3. Functia ![]() este diferentiabila in punctul
este diferentiabila in punctul ![]() daca si numai daca exista doua numere reale
daca si numai daca exista doua numere reale ![]() si
si ![]() si doua functii
si doua functii ![]() si
si ![]() definite pe
definite pe ![]() , continue
in
, continue
in ![]() si nule in acest punct,
si nule in acest punct, ![]() ,
, ![]() , astfel
incat pentru orice
, astfel
incat pentru orice ![]() ,
,
![]()
Aceasta egalitate se mai scrie
![]()
Propozitia 4. Daca
functia ![]() este diferentiabila in
este diferentiabila in ![]() , atunci ea
are derivate partiale in
, atunci ea
are derivate partiale in ![]() si
si ![]() ,
, ![]() .
.
Egalitatea de definitie a diferentiabilitatii se scrie atunci astfel:
![]()
Corolar. Daca ![]() este diferentiabila pe
este diferentiabila pe ![]() , atunci ea
are derivate partiale
, atunci ea
are derivate partiale ![]() si
si ![]() pe
pe ![]() .
.
Propozitia 5. Daca ![]() este diferentiabila in punctul
este diferentiabila in punctul ![]() , atunci ea
este continua in acest punct.
, atunci ea
este continua in acest punct.
Corolar. Daca ![]() este diferentiabila pe
este diferentiabila pe ![]() atunci ea este continua pe
atunci ea este continua pe ![]() .
.
Ultimele doua propozitii arata ca existenta unei derivate partiale si continuitatea unei functii sunt conditii necesare (dar nu suficiente) pentru diferentiabilitatea sa. Propozitia urmatoare da conditii suficiente de diferentiabilitate.
Propozitia 6. Daca ![]() are derivate partiale
are derivate partiale ![]() si
si ![]() intr-o vecinatate
intr-o vecinatate ![]() a lui
a lui ![]() si daca aceste derivate partiale sunt continue
in
si daca aceste derivate partiale sunt continue
in ![]() , atunci
functia
, atunci
functia ![]() este diferentiabila in
este diferentiabila in ![]() .
.
Reciproca propozitiei nu este adevarata.
Fie ![]() o functie reala definita pe
o functie reala definita pe ![]() si diferentiabila in
si diferentiabila in ![]() . Cum
. Cum ![]() are limita 0 in
are limita 0 in ![]() avem aproximarea:
avem aproximarea:
![]()
![]()
se numeste
diferentiala lui ![]() in
in ![]() .
.
Fie
functiile ![]()
![]() date de
date de ![]()
![]() atunci
atunci ![]() ,
, ![]() si
si ![]() ,
, ![]() , deci
, deci ![]() si
si ![]() .
.
Notand ![]() si
si ![]() vom avea
vom avea
![]()
![]()
Pentru o
functie de ![]() variabile
variabile ![]() diferentiala este
diferentiala este
![]()
unde ![]() este diferentiala functiei
este diferentiala functiei ![]() .
.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3284
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved