| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Inegalitati intre liniile importante in triunghi
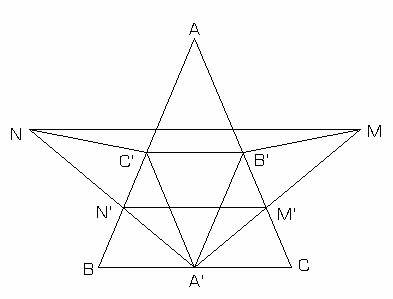 Aplicatia
II.7.1: Sa se arate ca in orice triunghi ABC are loc
inegalitatea:
Aplicatia
II.7.1: Sa se arate ca in orice triunghi ABC are loc
inegalitatea: ![]()
fig.II.7.1
Solutie:
Fie triunghiul ABC si A'B'C' mijloacele laturilor (BC), (CA),
(AB). Fie ![]() astfel incat
astfel incat ![]() si M simetricul
lui A' fata AC. Fie
si M simetricul
lui A' fata AC. Fie ![]() astfel incat
astfel incat ![]() si N simetricul lui A' fata de AB. Se
observa ca
si N simetricul lui A' fata de AB. Se
observa ca
![]() (1)
(1)
Cum triunghiurile MM'B si A'M'B' sunt congruente (L.U.L) obtinem:
![]() (2)
(2)
De asemenea ![]() (L.U.L.) ceea ce
implica
(L.U.L.) ceea ce
implica
![]() (3).
(3).
Inlocuind (2) si (3) in (1) deducem ca: ![]() si cum A'B'C'
sunt mijloacele laturilor (BC), (CA), (AB) obtinem:
si cum A'B'C'
sunt mijloacele laturilor (BC), (CA), (AB) obtinem:
![]() (4)
(4)
Prin constructie , M'N' este linie mijlocie in triunghiul A'MN, ceea ce conduce la:
![]() MN= 2M'N' (5), dar din
teorema sinusurilor (in triunghiul A'N'M') deducem
MN= 2M'N' (5), dar din
teorema sinusurilor (in triunghiul A'N'M') deducem
![]() (6)
(6)
Cum ![]() obtinem ca
patrulaterul AN'A'M' este inscriptibil si, deci
obtinem ca
patrulaterul AN'A'M' este inscriptibil si, deci ![]() adica:
adica: ![]() si din:
si din: ![]() (7)
(7)
Iar ![]() (8)
(8)
In triunghiul A'M'A, ![]() ,
,![]() de unde obtinem:
de unde obtinem: ![]() (9)
(9)
Inlocuind (7), (8) si (9) in (6) deducem succesiv ![]() ceea ce conduce
la:M'N'=AA'
ceea ce conduce
la:M'N'=AA'![]() ,adica
,adica ![]() dar avand in vedere
(5) obtinem:
dar avand in vedere
(5) obtinem: ![]() iar relatia (4) devine
iar relatia (4) devine ![]() ceea ce implica:
ceea ce implica:
![]() , care este
echivalenta cu
, care este
echivalenta cu ![]() , adica:
, adica: ![]() si prin urmare:
si prin urmare: ![]() , deci
, deci ![]() , cu egalitate in cazul triunghiului echilateral.
, cu egalitate in cazul triunghiului echilateral.
Aplicatia II.7.2. Sa se demonstreze ca in orice triunghi ABC au loc inegalitatile:
1) ![]()
2) ![]()
Solutie:
1)Se stie ca: ![]() ,prin urmatoarele:
,prin urmatoarele: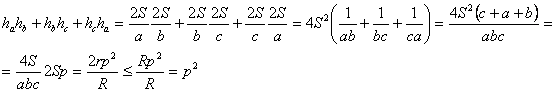
 ceea ce conduce la:
ceea ce conduce la: ![]() cu egalitate in cazul triunghiului echilateral.
cu egalitate in cazul triunghiului echilateral.
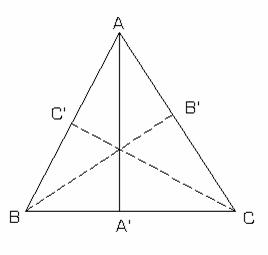
2) Fie triunghiul ABC si ![]()
astfel incat ![]() (fig.II.7.2)
(fig.II.7.2)
In triunghiul AA'B,![]() ceea ce implica:
ceea ce implica:
c>ha .
In triunghiul ACC',![]() si deci b>hc,
si deci b>hc,
iar in triunghiul BB'C,![]() de unde a>hb
de unde a>hb
fig.II.7.2
Prin urmare, c>ha , b>hc si a>hb ceea ce conduce la a+b+c>ha+hb+hc si deci: ha+hb+hc>2p
Aplicatia
II.7.3: Fie ABC un triunghi dreptunghic cu ![]() (fig. II.7.3.)Atunci are loc inegalitatea :
(fig. II.7.3.)Atunci are loc inegalitatea :
![]()
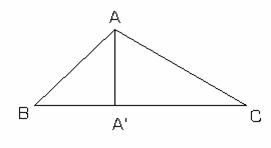
fig.II.7.3
Solutie:
Se stie ca :![]() si
si ![]() . Prin urmare, inegalitatea din enunt devine:
. Prin urmare, inegalitatea din enunt devine: ![]() (*)
(*)
Din relatia ![]() obtinem
obtinem![]() deci pentru a demonstra (*) este suficient sa verificam:
deci pentru a demonstra (*) este suficient sa verificam:
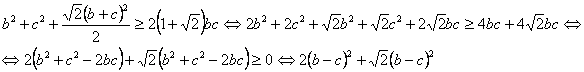
care este adevarata Egalitate avem daca b=c, adica in cazul triunghiului dreptunghic isoscel.
Aplicatia II.7.4: Sa se demonstreze ca in orice triunghi ABC au loc inegalitatile:
 1)
1)![]()
2)![]()
3)![]()
Solutie:
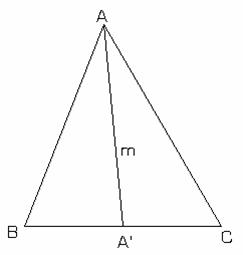
1) Fie triunghiul ABC si ![]() (fig.II.7.4)
(fig.II.7.4)
In triunghiul ABA': ![]() , iar in triunghiul
, iar in triunghiul
ACA': ![]() , deci 2ma=a+b+c, de unde ma<p
, deci 2ma=a+b+c, de unde ma<p
Celelalte relatii se obtin in mod analog.
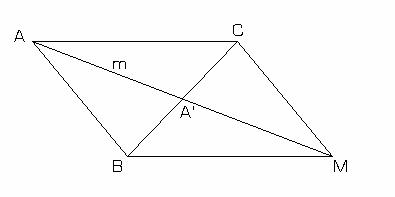 fig.II.7.4
fig.II.7.4
2) Fie triunghiul ABC si ![]()
Consideram punctul M ca fiind simetricul lui A
fata de mijlocul segmentului (BC) (fig.II.7.5)
Prin urmare AM=AA'+A'M=ma+ma.
Triunghiurile AA'C si MA'B sunt congruente
(L.U.L) ceea ce implica: BM=AB=b
In triunghiul ABM avem: AM<AB+BM, ceea
ce implica 2ma <b+c. fig.II.7.5
Celelalte relatii se obtin in mod similar
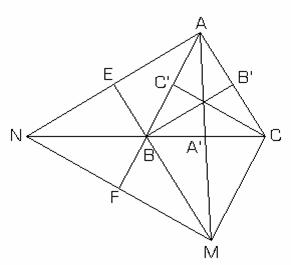 3) Fie triunghiul ABC si
3) Fie triunghiul ABC si ![]() astfel incat AA', BB',
CC' sunt mediane (fig.II.7.6)
astfel incat AA', BB',
CC' sunt mediane (fig.II.7.6)
conform punctului 2) avem:
![]()
![]() ceea ce implica
ceea ce implica
![]()
adica ![]() (*)
(*)
Consideram punctul N ca fiind
intersectia dreptei BC cu paralela
prin A la mediana BB'. Notam cu
![]() , unde M este simetricul
, unde M este simetricul
lui A fata de mijlocul segmentului (BC),
iar cu ![]() fig.II.7.6
fig.II.7.6
Observam ca AEBB' este paralelogram de unde rezulta ca EB=AB'=b/2 si cu BM=AC=b, obtinem ME=3b/2.
In triunghiul MNA avem: NA' este mediana iar BE=ME/3 si
BM=2ME/3 prin urmare, NA', ME si AF sunt mediane ![]() .
.
De asemenea, AM=2ma, NM=2mc, AN=2mb,
iar ![]() (**)
(**)
Conform relatiilor din punctul 2) vom avem in triunghiul ANM: 2AF<AN+AM, 2ME<MA+MN, 2NA'<NA+NM, dar avand in vedere relatiile (**) obtinem:
![]() de unde rezulta
3(a+b+c)<4(ma+mb+mc) care este
echivalenta cu :
de unde rezulta
3(a+b+c)<4(ma+mb+mc) care este
echivalenta cu : ![]() , dar
, dar ![]() si deci p<ma+mb+mc, care impreuna cu (*) ne da dubla
inegalitate din enunt.
si deci p<ma+mb+mc, care impreuna cu (*) ne da dubla
inegalitate din enunt.
Aplicatie
II.7.5: Se considera triunghiul ABC si ma,mb,mc
respectiv lungimea 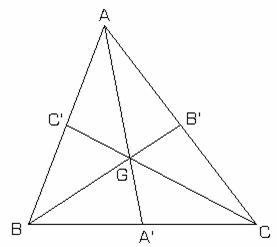 medianelor corespunzatoare laturilor BC,
AC, AB. Sa se arate ca a>b>c daca si numai daca
ma<mb<mc
medianelor corespunzatoare laturilor BC,
AC, AB. Sa se arate ca a>b>c daca si numai daca
ma<mb<mc
Solutie:
Fie triunghiul ABC, A'B'C' mijloacele
laturilor (BC), (AC),(AB) si G centrul
de greutate al triunghiul ABC (fig.II.7.7)
"=>" presupunem a>b>c. deoarece
in triunghiurile AC'C si BC'C avem
![]() ,
,
Obtinem conform teoremei II.1.8 ca
![]()
Prin urmare in triunghiurile AC'G si BC'G,
avem ![]() si fig.II.7.7
si fig.II.7.7
![]() obtinem conform
teoremei II.1.8 ca BG>AG dar BG=2mb/3
obtinem conform
teoremei II.1.8 ca BG>AG dar BG=2mb/3
iar AG=2ma/3 ceea ce implica ![]() .
.
Analog se demonstreaza ca![]() si deci
si deci ![]() .
.
"<=" presupunem ca ![]() . Cum
. Cum ![]() obtinem
obtinem ![]() de unde
de unde ![]() . Deci in triunghiurile AC'G si BC'G avem
. Deci in triunghiurile AC'G si BC'G avem ![]()
de unde rezulta ![]() Prin urmare comparand
triunghiurile AC'C si BC'C avem AC'=BC'
Prin urmare comparand
triunghiurile AC'C si BC'C avem AC'=BC' ![]() ceea ce implica
ceea ce implica ![]() , deci
, deci ![]() In mod analog, avem
In mod analog, avem ![]() si deci:
si deci: ![]() .
.
Aplicatia II.7.6: Se noteaza cu M,N si P respectiv mijloacele laturilor (BC); (AC) si (AB) ale triunghiul ABC oarecare. Dreptele AM , BN si CP intersecteaza cercul circumscris triunghiul ABC in Q,S,T (fig.II.7.8). Sa se arate ca:
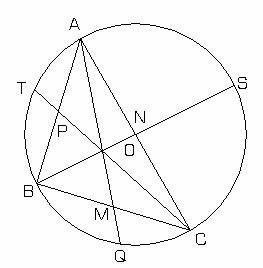
![]()
Solutie:
Puterea punctului M fata de cerc implica:
AM/MQ=BM/BC dar BM=MC=A/2 iar
AM=ma de unde rezulta ![]() deci
deci
![]() . In mod analog obtinem
. In mod analog obtinem ![]()
si ![]() . Avand cele trei relatii si folosind
. Avand cele trei relatii si folosind
teorema medianei avem:
![]() fig.II.7.8
fig.II.7.8
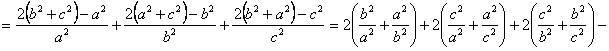
![]() .
.
In concluzie ![]() .
.
 Aplicatia
II.7.7: Se considera triunghiul ABC in care:
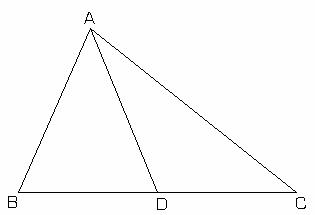
Aplicatia
II.7.7: Se considera triunghiul ABC in care: ![]() si D mijlocul lui
(BC)
si D mijlocul lui
(BC)
(fig.II.7.9). Sa se arate ca ![]()
Solutie:
Din ipoteza ![]()
dar ![]() ,
,
prin urmare: ![]() , ceea
, ceea
ce conduce la ![]() conform teoremei
conform teoremei
II.1.3 in triunghiul ABD sau
![]() , deci in triunghiul ADC, fig.II.7.9
, deci in triunghiul ADC, fig.II.7.9
conform teoremei II.1.3 deducem ca ![]() . Deci
. Deci ![]() sau
sau ![]() , ceea ce implica
, ceea ce implica ![]() .
.
Aplicatia II.7.8
(Problema 2'717 G.M. nr.3/1989): Daca a,b,c sunt laturile unui triunghi,
iar ![]() sunt lungimile
medianelor corespunzatoare acestor laturi, atunci avem:
sunt lungimile
medianelor corespunzatoare acestor laturi, atunci avem: ![]() .
.
Solutie:
Conform aplicatiei II.7.4 putem scrie: ![]() .
.
Aplicand inegalitatea mediilor pentru ![]() si
si ![]() obtinem:
obtinem:
![]() si in mod analog
deducem ca:
si in mod analog
deducem ca: ![]() si
si ![]() . Prin urmare,
. Prin urmare, ![]() si inegalitate
din enunt este demonstrata.
si inegalitate
din enunt este demonstrata.
Aplicatia
II.7.9: Sa se arate ca intr-un triunghi oarecare ABC: ![]() .
.
Solutie:
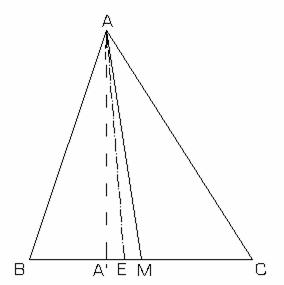 Fie triunghiul ABC si
Fie triunghiul ABC si ![]() astfel incat
astfel incat ![]() Avem
Avem ![]() si
si ![]() (*).
(*).
Din teorema bisectoarei ![]() .
.
Deducem ![]() de unde
de unde ![]()
si deci![]() adica
adica ![]() ceea ce
ceea ce
implica ![]() .
.
Utilizand teorema lui Pitagora in triunghiurile
![]() si
si ![]() reiese
reiese
ca: ![]() si
si
obtinem: ![]() (**). Prin urmare din
relatiile
(**). Prin urmare din
relatiile
(*) si (**) obtinem ![]() . Daca
. Daca
triunghiul ABC este isoscel, ![]() ,
,
inaltimea, bisectoarea interioara si mediana
duse din A coincid si, drept urmare ![]() . fig.II.7.10
. fig.II.7.10
Aplicatia
II.7.10: Daca intr-un triunghi ABC avem ![]() , atunci
, atunci ![]() .
.
Solutie:
Avem: ![]()
![]() , dar
, dar ![]() ,
, ![]() , implica:
, implica: ![]() ceea ce este
echivalent cu
ceea ce este
echivalent cu ![]() . Egalitatea este verificata pentru a=b sau
. Egalitatea este verificata pentru a=b sau ![]() , deci cand triunghiul ABC este isoscel cu varful in C sau
dreptunghic cu
, deci cand triunghiul ABC este isoscel cu varful in C sau
dreptunghic cu ![]() .
.
Aplicatia II.7.11: Sa se arate ca in orice triunghi ABC are loc inegalitatea:
![]() ,
, ![]() ,
, ![]()
Solutie:
Din teorema medianei avem: ![]() , dar
, dar ![]() si deci
rezulta
si deci
rezulta ![]() de unde obtinem:
de unde obtinem: ![]() (1) cu egalitate
pentru b=c.
(1) cu egalitate
pentru b=c.
Pe de alta parte,![]() , conduce la
, conduce la ![]() . Celelalte relatii se deduc in mod
asemanator.
. Celelalte relatii se deduc in mod
asemanator.
Aplicatia II.7.12: In orice triunghi au loc inegalitatile:
![]()
Solutie:
![]()
![]() adevarat.
adevarat.
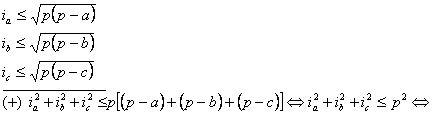
![]() Avem egalitate pentru
triunghiul echilateral.
Avem egalitate pentru
triunghiul echilateral.
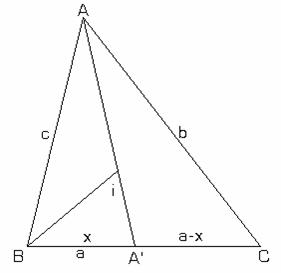
Fie i centrul cercului circumscris (fig.II.7.11).
Exprimam pe AI: In ![]()
In ![]()
![]()
![]()
![]()
Fie ![]() .
.
In triunghiul IBC (fig.II.7.12):
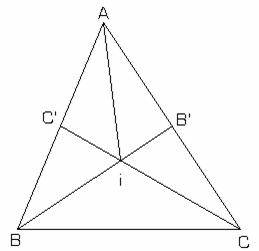
![]() fig.II.7.11
fig.II.7.11
![]()
![]()
Deci ![]()
fig.II.7.12
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3084
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved