| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Progresii aritmetice si geometrice
Generalitati
Definitie. Se
numeste sir de numere reale
orice functie ![]() , unde
, unde ![]() este o
submultime finita a lui
este o
submultime finita a lui ![]() .
.
Exemple :
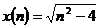 ,
,
Vom presupune in general ca ![]() . Fie deci
. Fie deci ![]() . Numarul
. Numarul ![]() se noteaza in
general cu
se noteaza in
general cu ![]() si se
numeste termenul de rang
si se
numeste termenul de rang ![]() al sirului
al sirului ![]() .
.
Notatie : Vom
nota sirul ![]() prin
prin ![]() sau
sau ![]() sau simplu
sau simplu ![]() .
.
Definitie.
Sirul ![]() se numeste marginit daca
exista doua numere reale
se numeste marginit daca
exista doua numere reale ![]() astfel incat
astfel incat ![]() ,
, ![]() .
.
Exemplu :
Sirul ![]() definit prin termenul
general
definit prin termenul
general ![]() ,
, ![]() este marginit
deoarece
este marginit
deoarece ![]() ,
, ![]() (aici
(aici ![]() si
si ![]() ).
).
Definitie.
Sirul ![]() este strict crescator (strict descrescator)
daca
este strict crescator (strict descrescator)
daca ![]() ,
, ![]() (
(![]() ,
,![]() ) .
) .
Observatii.
Exemplu :
Fie sirul ![]() de mai sus, cu
de mai sus, cu ![]() . Pentru a preciza monotonia sirului
. Pentru a preciza monotonia sirului ![]() se calculeaza
diferenta
se calculeaza
diferenta ![]() ,
, ![]() , ceea ce arata ca
, ceea ce arata ca ![]() sau
sau ![]() ,
, ![]() , adica sirul
, adica sirul ![]() este strict
crescator.
este strict
crescator.
Moduri de a defini un sir :
1. Printr-o
regula de calcul. In aceasta situatie se precizeaza o
exprimare analitica pentru termenul de rang ![]() ,
, ![]() , care permite calcularea oricarui termen al
sirului.
, care permite calcularea oricarui termen al
sirului.
Exemple :
1. Daca sirul
![]() este dat prin
este dat prin ![]() ,
, ![]() , atunci se poate calcula orice termen din sir. De
exemplu
, atunci se poate calcula orice termen din sir. De
exemplu ![]() ,
, ![]() ,
, ![]() , etc.
, etc.
2. Daca ![]() este sirul dat
prin termenul general
este sirul dat
prin termenul general ![]() ,
, ![]() , atunci
, atunci ![]() ,
, ![]() , etc.
, etc.
2. Prin mai multe reguli de calcul.
Fie sirul ![]() cu termenul general
cu termenul general ![]() .
.
Avem ![]() (
(![]() , impar) ,
, impar) , ![]() (
(![]() , par),
, par), ![]() (
(![]() , impar).
, impar).
3. Printr-o relatie de recurenta.
In acest caz un termen al sirului se exprima in functie de unul sau mai multi termeni precedenti. Pentru a determina bine elementele sirului trebuie precizati unul sau mai multi termeni.
Exemple :
1. ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Observam
ca aceasta relatie se poate scrie si sub forma ![]() ,
, ![]() , adica diferenta a oricaror doi termeni
consecutivi din sir este constanta .
, adica diferenta a oricaror doi termeni
consecutivi din sir este constanta .
2. ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
In acest caz catul a
oricaror doi termeni consecutivi ai sirului ![]() este constant.
este constant.
3. ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Un termen al sirului incepand cu al treilea este egal cu
suma precedentilor doi.
. Un termen al sirului incepand cu al treilea este egal cu
suma precedentilor doi.
Determinarea
oricarui termen se face din aproape in aproape : ![]() ,
, ![]()
![]() ,
, ![]() , etc.
, etc.
Progresii aritmetice
Definitie.
Sirul ![]() pentru care fiecare
termen al sau, incepand cu al doilea se obtine din precedentul prin
adaugarea aceluiasi numar
pentru care fiecare
termen al sau, incepand cu al doilea se obtine din precedentul prin
adaugarea aceluiasi numar ![]() se numeste progresie aritmetica.
Numarul
se numeste progresie aritmetica.
Numarul ![]() se numeste ratia progresiei.
se numeste ratia progresiei.
Observatie. Deci
![]() este progresie
aritmetica daca avem relatia de recurenta
este progresie
aritmetica daca avem relatia de recurenta ![]() ,
, ![]() . Asadar pentru a proba ca sirul
. Asadar pentru a proba ca sirul ![]() este progresie
aritmetica trebuie aratat ca diferenta a doi termeni consecutivi
este progresie
aritmetica trebuie aratat ca diferenta a doi termeni consecutivi
![]() este constanta :
este constanta :
![]() constant,
constant, ![]() .
.
Notatie : Faptul
ca ![]() este o progresie
aritmetica se marcheaza prin :
este o progresie
aritmetica se marcheaza prin : ![]()
Se spune ca numerele ![]() sunt in progresie aritmetica daca sunt termeni
consecutivi ai unei progresii aritmetice.
sunt in progresie aritmetica daca sunt termeni
consecutivi ai unei progresii aritmetice.
Exemplu :
Se considera sirul ![]() cu termenul general
cu termenul general ![]() ,
, ![]() .
.
1. Pentru a preciza daca sirul este
progresie aritmetica calculam diferenta a doi termeni
consecutivi oarecare ![]() ,
, ![]() si avem :
si avem :
![]() constant,
constant, ![]() .
.
Cum aceasta diferenta este
constanta, egala cu 7, ea reprezinta ratia progresiei
aritmtice. Deci ![]() . Primul termen este
. Primul termen este ![]() . Avem :
. Avem : ![]() .
.
2. Un numar ![]() este termen al
sirului
este termen al
sirului ![]() daca exista
daca exista ![]() pentru care
pentru care ![]() . A-l determina pe
. A-l determina pe ![]() inseamna sa
rezolvam ecuatia
inseamna sa
rezolvam ecuatia ![]() . Numarul natural
. Numarul natural ![]() (daca
exista) reprezinta rangul termenului din sir care este egal cu
(daca
exista) reprezinta rangul termenului din sir care este egal cu ![]() .
.
Pentru ![]() , avem
, avem ![]() cu solutia
cu solutia ![]() . Deci numarul
. Deci numarul ![]() este termenul
este termenul ![]() .
.
Pentru ![]() se obtine
ecuatia
se obtine
ecuatia ![]() cu solutia
cu solutia ![]() care insa nu este
numar natural. Deci nu exista termen al sirului care sa fie
egal cu 235.
care insa nu este
numar natural. Deci nu exista termen al sirului care sa fie
egal cu 235.
In fine, pentru ![]() , ecuatia
, ecuatia ![]() are solutia
are solutia ![]() . Prin urmare numarul
. Prin urmare numarul ![]() este termen al
sirului si anume
este termen al
sirului si anume ![]() .
.
Propozitie.
Progresia aritmetica ![]() este un sir :
este un sir :
Demonstratie. Din ![]() ,
, ![]() se deduce imediat
afirmatia.
se deduce imediat
afirmatia.
Propozitie
(Formula termenului general). Daca sirul
![]() este o progresie
aritmetica, avand primul termen
este o progresie
aritmetica, avand primul termen ![]() si ratia
si ratia ![]() , atunci termenul general are forma :
, atunci termenul general are forma :
![]() ,
, ![]() .
.
Demonstratie. Se face prin inductie matematica :
Consideram propozitia ![]() ,
, ![]() .
.
Pasul1.
Verificarea : ![]() , afirmatie adevarata.
, afirmatie adevarata.
Pasul 2. ![]() :
:
Presupunem ![]() adevarata
si demonstram
adevarata
si demonstram ![]() , cu alte cuvinte ca propozitia
, cu alte cuvinte ca propozitia ![]() este
adevarata. Avem :
este
adevarata. Avem :
![]()
si deci ![]() este
adevarata.
este
adevarata.
Pasul 3.
Finalizarea : ![]() ,
, ![]() .
.
Propozitie. Sirul
![]() este o progresie
aritmetica daca si numai daca orice termen al sau,
incepand cu al doilea, este medie aritmetica a vecinilor sai,
adica daca
este o progresie
aritmetica daca si numai daca orice termen al sau,
incepand cu al doilea, este medie aritmetica a vecinilor sai,
adica daca
![]() ,
, ![]() .
.
Demonstratie. Daca sirul ![]() este o progresie
aritmetica de ratie
este o progresie
aritmetica de ratie ![]() , atunci
, atunci ![]() ,
, ![]() . Adunand cele doua relatii, membru cu membru,
obtinem
. Adunand cele doua relatii, membru cu membru,
obtinem ![]() , de unde
, de unde ![]() .
.
Reciproc, din relatia ![]() , scrisa sub forma
, scrisa sub forma ![]() sau
sau ![]()
![]() ,
, ![]() se deduce ca
diferenta a doi termeni consecutivi ai sirului este constanta,
ceea ce arata ca sirul
se deduce ca
diferenta a doi termeni consecutivi ai sirului este constanta,
ceea ce arata ca sirul ![]() este o progresie
aritmetica.
este o progresie
aritmetica.
Observatie. Are loc relatia mai generala :
![]() ,
, ![]() .
.
Propozitie.
Daca numerele ![]() sunt in progresie
aritmetica, atunci
sunt in progresie
aritmetica, atunci
![]() ,
, ![]() .
.
(Suma
oricaror doua numere egal departate de numerele extreme ![]() este egala cu
suma numerelor extreme
este egala cu
suma numerelor extreme ![]() ).
).
Demonstratie. Se scriu toti termenii in functie de primul termen ![]() si ratia
si ratia ![]() . Avem :
. Avem :
![]() si
si ![]()
![]() , ceea ce probeza afirmatia.
, ceea ce probeza afirmatia.
Propozitie (Suma
primilor n termeni). Daca ![]() este o progresie
aritmetica, atunci
este o progresie
aritmetica, atunci
![]() ,
, ![]() .
.
(Suma
primilor ![]() termeni ai unei
progresii aritmetice este egala cu produsul dintre semisuma termenilor
extremi si numarul termenilor sumei).
termeni ai unei
progresii aritmetice este egala cu produsul dintre semisuma termenilor
extremi si numarul termenilor sumei).
Demonstratie. Scriem de doua ori suma ![]() ,
,
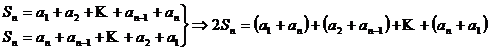 .
.
Tinand cont de propzitia
precedenta, fiecare paranteza este egala cu ![]() . Asadar
. Asadar ![]() , adica
, adica ![]() .
.
Observatie. Suma
![]() se poate exprima in
functie de primul termen
se poate exprima in
functie de primul termen ![]() si ratia
si ratia ![]() , astfel :
, astfel :
![]() .
.
Observatie.
Termenul general ![]() se poate exprima cu
ajutorul sumelor
se poate exprima cu
ajutorul sumelor ![]() . Mai precis
. Mai precis
![]() ,
, ![]() .
.
Exercitii rezolvate :
1. Progresia aritmetica ![]() de ratie
de ratie ![]() este definita
prin elementele sale. Determinati in fiecare din cazuri, elementul cerut .
este definita
prin elementele sale. Determinati in fiecare din cazuri, elementul cerut .
a)
![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
b)
![]() . Calculati
. Calculati ![]() ;
;
c)
![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
d) ![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
e)
![]() ,
, ![]() . Calculati
. Calculati ![]() si
si ![]() ;
;
f)
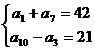 . Calculati
. Calculati ![]() si
si ![]() .
.
a) Formula termenului general este : ![]() . Pentru
. Pentru ![]() , avem
, avem ![]()
![]() .
.
b) Din ![]() deducem
deducem ![]() .
.
c) Din ![]() se obtine
se obtine ![]() si deci
si deci ![]() .
.
d) Avem ![]() , iar de aici
, iar de aici ![]() . Avem
. Avem ![]() .
.
e) Avem sistemul 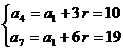 cu solutia
cu solutia ![]() ,
, ![]() .
.
f) Se scriu cele doua relatii in
functie de ![]() si
si ![]() si avem sistemul
:
si avem sistemul
:
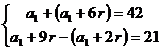 cu solutia
cu solutia ![]() ,
, ![]() .
.
2. Daca numerele ![]() sunt in progresie
aritmetica, sa se calculeze sumele :
sunt in progresie
aritmetica, sa se calculeze sumele :
![]() ,
,
![]() ,
, ![]()
in functie de ![]() ,
, ![]() si
si ![]() .
.
Ideea este de a scrie un termen oarecare al fiecarei sume ca diferenta de doi termeni de acelasi tip. Pentru prima suma avem :
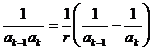 ,
, ![]() . Atunci :
. Atunci :
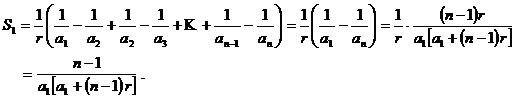
Pentru a doua suma, termenul general este (se rationalizeaza) :
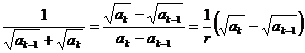 ,
, ![]() . Deci :
. Deci :
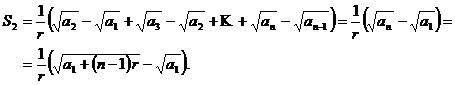
3. Sa se arate ca numerele ![]() ,
, ![]() ,
, ![]() nu pot fi termenii
unei progresii aritmetice.
nu pot fi termenii
unei progresii aritmetice.
Presupunem, prin reducere la absurd, ca
aceste numere sunt termenii (nu neaparat consecutivi) ai unei progresii
aritmetice. Fie deci ![]() ,
, ![]() ,
, ![]() si sa
admitem ca
si sa
admitem ca ![]() sunt diferite intre
ele. Atunci
sunt diferite intre
ele. Atunci ![]() ,
, ![]() ,
, ![]() ,
, ![]() . De aici
. De aici ![]() ,
, ![]()
![]() . Impartind membru cu membru aceste relatii,
rezulta :
. Impartind membru cu membru aceste relatii,
rezulta : ![]() . Cum membrul stang
este rational, il notam cu
. Cum membrul stang
este rational, il notam cu ![]() . Deci
. Deci ![]() sau
sau ![]() , care prin ridicare la patrat devine :
, care prin ridicare la patrat devine : ![]() , ceea ce este absurd, deoarece membrul stang este
irational iar membrul drept este rational. In concluzie
, ceea ce este absurd, deoarece membrul stang este
irational iar membrul drept este rational. In concluzie ![]() ,
, ![]() ,
, ![]() nu pot fi termenii
unei progresii aritmetice.
nu pot fi termenii
unei progresii aritmetice.
4. Daca ![]() reprezinta suma
primilor
reprezinta suma
primilor ![]() termeni ai
sirului
termeni ai
sirului ![]() atunci :
atunci :
a) Sa se determine termenul general ![]() ;
;
b) Sa se arate ca sirul ![]() este o progresie aritmetica.
este o progresie aritmetica.
a) Din relatia ![]() ,
, ![]() , rezulta :
, rezulta :
![]() ,
, ![]() .
.
b) Calculam diferenta a doi termeni consecutivi
![]() ,
, ![]() , si constatam ca
, si constatam ca ![]() este ratia
progresiei in care
este ratia
progresiei in care ![]() .
.
Observatie.S-ar
fi putut calcula ![]() si
si ![]() din
din ![]() ,
, ![]() . De aici
. De aici ![]() si deci
si deci ![]() . Se verifica usor ca pentru
. Se verifica usor ca pentru ![]() si
si ![]() suma
suma ![]() reprezinta suma
primilor
reprezinta suma
primilor ![]() termeni ai acestei
progresii aritmetice.
termeni ai acestei
progresii aritmetice.
4. Sa se rezolve ecuatia : ![]() .
.
Sa observam ca termenii sumei
sunt in progresie aritmetica de ratie ![]() . Notam
. Notam ![]() . Atunci suma din stanga egalitatii devine :
. Atunci suma din stanga egalitatii devine :
![]() . Rezolvand aceasta ecuatie gasim
. Rezolvand aceasta ecuatie gasim ![]() si deci
si deci ![]() .
.
Progresii geometrice
Definitie.
Sirul ![]() cu
cu ![]() (primul termen) pentru
care fiecare termen al sau, incepand cu al doilea, se obtine din
precedentul prin inmultirea cu acelati numar
(primul termen) pentru
care fiecare termen al sau, incepand cu al doilea, se obtine din
precedentul prin inmultirea cu acelati numar ![]() se numeste progresie geometrica. Numarul
se numeste progresie geometrica. Numarul ![]() se numeste ratia progresiei.
se numeste ratia progresiei.
Observatie. Deci
![]() este progresie
geometrica daca avem relatia de recurenta
este progresie
geometrica daca avem relatia de recurenta ![]() ,
, ![]() . Asadar pentru a
proba ca sirul
. Asadar pentru a
proba ca sirul ![]() este o progresie
geometrica trebuie aratat ca raportul a doi termeni consecutivi
este o progresie
geometrica trebuie aratat ca raportul a doi termeni consecutivi ![]() ,
, ![]() este constant :
este constant :
![]() constant,
constant, ![]() .
.
Notatie. Faptul
ca sirul ![]() este o progresie
geometrica se marcheaza uneori prin
este o progresie
geometrica se marcheaza uneori prin
![]()
![]() . Spunem ca numerele
. Spunem ca numerele ![]() sunt in progresie geometrica daca sunt termeni
consecutivi ai unei progresii geometrice.
sunt in progresie geometrica daca sunt termeni
consecutivi ai unei progresii geometrice.
Exemplu :
Fie sirul ![]() cu termenul general
cu termenul general ![]() ,
, ![]() .
.
a) Sa se stabileasca daca sirul dat este o progresie geometrica, calculand apoi primii cinci termeni.
b) Stabiliti care din numerele de mai jos este termen al progresiei : 24, 96, 123.
a) Pentru a vedea daca sirul este o progresie geometrica se calculeaza raportul a doi termeni consecutivi :
![]() ,
, ![]() .
.
Cum acest raport este constant (nu depinde de
rangul ![]() ) deducem ca sirul este o progresie geometrica
de ratie
) deducem ca sirul este o progresie geometrica
de ratie ![]() , avand primul termen
, avand primul termen ![]() . Avem
. Avem ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
b) A stabili daca un numar ![]() este un termen al
sirului revine la a determina rangul
este un termen al
sirului revine la a determina rangul ![]() pentru care
pentru care ![]() .
.
Pentru ![]() din
din ![]() rezulta
rezulta ![]() , adica
, adica ![]() . Asadar
. Asadar ![]() . Daca
. Daca ![]() , atunci din
, atunci din ![]() rezulta
rezulta ![]() , adica
, adica ![]() . Deci
. Deci ![]() . In fine, pentru
. In fine, pentru ![]() din
din ![]() rezulta
rezulta ![]() . Cum aceasta ecuatie nu are solutie in
. Cum aceasta ecuatie nu are solutie in ![]() , deducem ca 123 nu este termen al sirului.
, deducem ca 123 nu este termen al sirului.
Propozitie. Fie ![]() o progresie geometrica
de ratie
o progresie geometrica
de ratie ![]() . Daca :
. Daca :
Demonstratie. Din ![]() ,
, ![]() si
informatiile despre
si
informatiile despre ![]() si
si ![]() conduc la concluziile
din proprietate.
conduc la concluziile
din proprietate.
Propozitie
(Formula termenului general). Daca sirul
![]() este o progresie
geometrica de ratie
este o progresie
geometrica de ratie ![]() , atunci termenul general
, atunci termenul general ![]() are forma :
are forma :
![]() ,
, ![]() .
.
Demonstratie. Se procedeaza prin inductie matematica.
Propozitie.
Sirul ![]() cu termeni nenuli este
o progresie geometrica daca si numai daca pentru orice
termen al sau, incepand cu al doilea avem :
cu termeni nenuli este
o progresie geometrica daca si numai daca pentru orice
termen al sau, incepand cu al doilea avem :
![]() ,
, ![]() .
.
Demonstratie. Presupunem ca sirul ![]() este o progresie
geometrica de ratie
este o progresie
geometrica de ratie ![]() si deci
si deci ![]() ,
, ![]() . De aici (se face produsul relatiilor)
. De aici (se face produsul relatiilor) ![]() .
.
Reciproc, din ![]() rezulta
rezulta ![]() ,
, ![]() . Aceasta ultima egalitate afirma ca
raportul oricaror doi termeni consecutivi, incepand cu al doilea este
constant. Deci sirul
. Aceasta ultima egalitate afirma ca
raportul oricaror doi termeni consecutivi, incepand cu al doilea este
constant. Deci sirul ![]() este progresie
geometrica.
este progresie
geometrica.
Observatie. Are loc relatia mai generala :
![]() ,
, ![]() .
.
Propozitie. Daca
numerele ![]() sunt in progresie
geometrica, atunci :
sunt in progresie
geometrica, atunci :
![]() ,
, ![]() .
.
(Produsul
oricaror doua numere egal departate de numerele ![]() este egal cu produsul
numerelor extreme
este egal cu produsul
numerelor extreme ![]() ).
).
Demonstratie. Screiem termenii in functie de primul termen ![]() si de ratia
si de ratia ![]() . Avem
. Avem ![]() si
si ![]() , ceea ce probeza afirmatia.
, ceea ce probeza afirmatia.
Propozitie (Suma
primilor n termeni). Daca ![]() este o progresie
geometrica de ratie
este o progresie
geometrica de ratie ![]() , atunci :
, atunci :
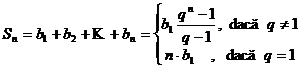 .
.
Demonstratie. Daca ![]() , atunci
, atunci ![]() , deci
, deci ![]() . Fie acum
. Fie acum ![]() . Consideram
. Consideram ![]() . Din aceasta relatie se scade
. Din aceasta relatie se scade ![]() si rezulta
si rezulta ![]() . Cum
. Cum ![]() , de aici rezulta
, de aici rezulta ![]() .
.
Exemrcitii rezolvate :
1. Progresia geometrica ![]() de ratie
de ratie ![]() este definita
prin anumite elemente date. Determinati in fiecare din cazuri, elementele
cerute.
este definita
prin anumite elemente date. Determinati in fiecare din cazuri, elementele
cerute.
a)
![]() . Calculati
. Calculati ![]() si
si ![]() ;
;
b)
![]() . Calculati
. Calculati ![]() si
si ![]() ;
;
c)
![]() ,
, ![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
d) ![]() ,
, ![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
e)
![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
f)
![]() . Calculati
. Calculati ![]() ;
;
g)
![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
h)
![]() . Calculati
. Calculati ![]() .
.
a) Din ![]() rezulta
rezulta ![]() , ceea ce da
, ceea ce da ![]() . Acum
. Acum ![]() .
.
b) Din ![]() rezulta
rezulta ![]() , iar de aici
, iar de aici ![]() . Acum cunoscand
. Acum cunoscand ![]() si
si ![]() , avem
, avem ![]() .
.
c) Din ![]() deducem
deducem ![]() sau
sau ![]() . Din
. Din ![]() , avem
, avem ![]() sau tinand seama
ca
sau tinand seama
ca ![]() mai putem scrie
mai putem scrie ![]() .
.
De aici ![]() si din prima
egalitate
si din prima
egalitate ![]() , adica
, adica ![]() .
.
d) Rescriem relatiile in functie de primul termen si de ratie. Avem sistemul :
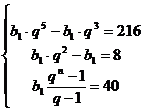 .
.
Sistemul format din primele doua ecuatii devine :
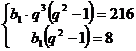 .
.
Impartind membru cu membru, cele
doua ecuatii gasim ![]() , adica
, adica ![]() . Din a doua ecuatie
. Din a doua ecuatie ![]() . In fine, din ultima ecuatie a sistemului initial
gasim
. In fine, din ultima ecuatie a sistemului initial
gasim ![]() .
.
e) Avem egalitatile (din scrierea
lui ![]() ,
, ![]() cu ajutorul lui
cu ajutorul lui ![]() si
si ![]() ) :
) :
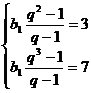 .
.
Daca ![]() , atunci
, atunci ![]() si
si ![]() devin relatii
imposibile. Prin urmare
devin relatii
imposibile. Prin urmare ![]() . Impartind membru cu membru, cele doua
ecuatii rezulta ecuatia
. Impartind membru cu membru, cele doua
ecuatii rezulta ecuatia ![]() cu solutiile
cu solutiile ![]() ,
, ![]() ,
, ![]() . Retinem numai ultimele doua valori.
. Retinem numai ultimele doua valori.
Daca ![]() , atunci
, atunci ![]() si deci
si deci ![]() , iar pentru
, iar pentru ![]() se obtine
se obtine ![]() cand
cand ![]() .
.
f) Din ![]() reulta
reulta ![]() sau
sau ![]() , iar de aici
, iar de aici ![]() da
da ![]() . Daca
. Daca ![]() si
si ![]() gasim
gasim ![]() , iar din
, iar din ![]() si
si ![]() deducem
deducem ![]() .
.
g) Pentru a exprima ![]() avem nevoie de
avem nevoie de ![]() si
si ![]() . Din egalitatea
. Din egalitatea ![]() deducem
deducem ![]() sau
sau ![]() , adica
, adica ![]() . Din
. Din ![]() avem
avem ![]() sau
sau ![]() . Acum
. Acum ![]() se calculeza
usor.
se calculeza
usor.
h) Din egalitatea ![]() sau
sau ![]() rezulta
rezulta ![]() , iar raportul
, iar raportul ![]() .
.
2. Sa se calculeze sumele :
a)
![]() ;
;
b)
![]() .
.
a) Sa observam ca termenii
sumei sunt in progresie geometrica de ratie ![]() , primul termen fiind
, primul termen fiind ![]() . In suma avem
. In suma avem ![]() termeni si deci
termeni si deci
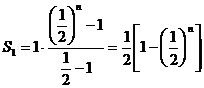 .
.
b) Pentru a calcula aceasta suma o vom imparti in mai multe sume, care fiecare in parte reprezinta suma unor termeni in progresie geometrica. Avem scrierea
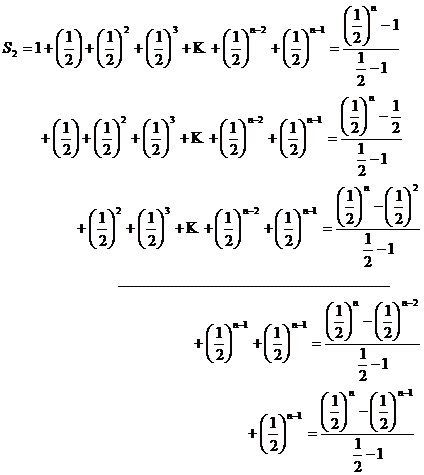
In total avem ![]() sume. Fiecare
suma este formata din termeni in progresie geometrica de
ratie
sume. Fiecare
suma este formata din termeni in progresie geometrica de
ratie ![]() . In dreapta fiecarei sume am aplicat formula de calcul
. In dreapta fiecarei sume am aplicat formula de calcul ![]() . Deci
. Deci ![]() are valoarea data
prin insumarea numerelor de la fiecare suma partiala, adica
are valoarea data
prin insumarea numerelor de la fiecare suma partiala, adica
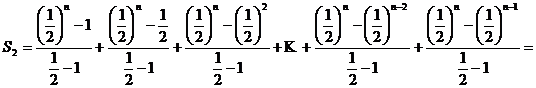
=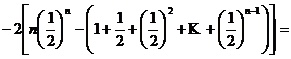
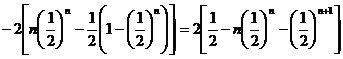 .
.
3. Sa se calculeze suma ![]() .
.
Folosim scrierea zecimala a unui numar si avem :
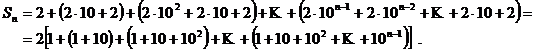
Observand ca in fiecare paranteza
rotunda avem de insumat termeni care sunt in progresie geometrica de
ratie ![]() .
.
Deci 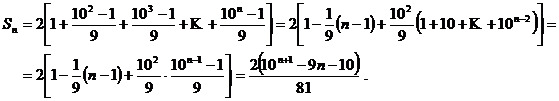
Subiecte propuse
1. Progresia aritmetica ![]() de ratie
de ratie ![]() este definita
prin anumite elemente date. Determinati in fieacre din cazuri, elementele
cerute.
este definita
prin anumite elemente date. Determinati in fieacre din cazuri, elementele
cerute.
a)
![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
b)
![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
c)
![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
d) ![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
e)
![]() . Calculati
. Calculati ![]() ;
;
f)
![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
g)
![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
h)
![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
i)
![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
j)
![]() ,
, ![]() . Calculati
. Calculati ![]() .
.
2. Progresia aritmetica ![]() de ratie
de ratie ![]() este definita
prin anumite elemente date. Determinati in fieacre din cazuri, elementele
cerute.
este definita
prin anumite elemente date. Determinati in fieacre din cazuri, elementele
cerute.
a)
![]() ,
, ![]() . Calculati
. Calculati ![]() si
si ![]() ;
;
b)
![]() . Calculati
. Calculati ![]() si
si ![]() ;
;
c)
![]() ,
, ![]() ,
, ![]() . Calculati
. Calculati ![]() si
si ![]() ;
;
d) ![]() ,
, ![]() . Calculati
. Calculati ![]() si
si ![]() ;
;
e)
![]() ,
, ![]() ,
, ![]() . Calculati
. Calculati ![]() si
si ![]() ;
;
f)
![]() ,
, ![]() . Calculati
. Calculati ![]() si
si ![]() ;
;
g)
![]() . Calculati
. Calculati ![]() ;
;
h)
![]() ,
, ![]() . Calculati
. Calculati ![]() si
si ![]() ;
;
i)
![]() ,
, ![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
j)
![]() . Calculati
. Calculati ![]() ;
;
k)
![]() ,
, ![]() . Calculati
. Calculati ![]() si
si ![]() ;
;
l)
![]() ,
, ![]() . Calculati
. Calculati ![]() si
si ![]() ;
;
m) ![]() . Calculati
. Calculati ![]() ;
;
n)
![]() ,
, ![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
o)
![]() ,
, ![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
p)
![]() ,
, ![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
q)
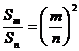 ,
, ![]() . Calculati
. Calculati ![]() ;
;
r)
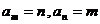 . Calculati
. Calculati ![]() ;
;
s)
![]() ,
, ![]() ,
,![]() . Calculati
. Calculati ![]() ;
;
t)
![]() ,
, ![]() . Calculati
. Calculati ![]() .
.
3. Progresia geometrica ![]() de ratie
de ratie ![]() este definita
prin anumite elemente date. Determinati, in fiecare din cazuri, elementele
cerute .
este definita
prin anumite elemente date. Determinati, in fiecare din cazuri, elementele
cerute .
a)
![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
b)
![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
c)
![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
d) ![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
e)
![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
f)
![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
g)
![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
h)
![]() ,
, ![]() . Calculati
. Calculati ![]() .
.
4. Progresia geometrica ![]() de ratie
de ratie ![]() este definita
prin anumite elemente date. Determinati, in fiecare din cazuri, elementele
cerute .
este definita
prin anumite elemente date. Determinati, in fiecare din cazuri, elementele
cerute .
a)
![]() ,
, ![]() ,
, ![]() . Calculati
. Calculati ![]() si
si ![]() ;
;
b)
![]() ,
, ![]() ,
, ![]() . Calculati
. Calculati ![]() si
si ![]() ;
;
c)
![]() ,
, ![]() ,
, ![]() . Calculati
. Calculati ![]() ,
, ![]() ;
;
d) ![]() ,
, ![]() ,
, ![]() . Calculati
. Calculati ![]() si
si ![]() ;
;
e)
![]() ,
, ![]() ,
, ![]() . Calculati
. Calculati ![]() ,
, ![]() ;
;
f)
![]() ,
, ![]() ,
, ![]() . Calculati
. Calculati ![]() ,
, ![]() ;
;
g)
![]() ,
, ![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
h)
![]() ,
, ![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
i)
![]() ,
, ![]() ,
, ![]() . Calculati
. Calculati ![]() si
si ![]() ;
;
j)
![]() ,
, ![]() . Calculati
. Calculati ![]() ;
;
k)
![]() ,
, ![]() . Calculati
. Calculati ![]() .
.
5. Determinati termenul general al
sirului ![]() definit prin
relatia de recurenta
definit prin
relatia de recurenta ![]() , daca
, daca ![]() .
.
6. Se considera sirul ![]() definit prin
relatia de recurenta
definit prin
relatia de recurenta ![]() ,
, ![]() .
.
a) Daterminati formula termenului general.
b)
Numarul ![]() este termen al
sirului ?
este termen al
sirului ?
7. Se considera sirul ![]() cu termenul general
cu termenul general ![]() ,
, ![]() .
.
a)
Stabiliti daca
sirul ![]() este o progresie
aritmetica .
este o progresie
aritmetica .
b) Stabiliti care din numerele de mai jos este termen al sirului dat :
1) 600,4; 2) 300; 3) 300,4.
8. Aratati ca numerele ![]() ,
, ![]() ,
, ![]() nu pot fi termenii
unei progresii geometrice.
nu pot fi termenii
unei progresii geometrice.
9. Fie ![]() patru numere in
progresie aritmetica. Daca din aceste numere se scad numerele 2, 5, 7
si respectiv 7 se obtin alte patru numere in progresie
geometrica. Sa se determine
patru numere in
progresie aritmetica. Daca din aceste numere se scad numerele 2, 5, 7
si respectiv 7 se obtin alte patru numere in progresie
geometrica. Sa se determine ![]() .
.
10. Fie sirul ![]() definit prin
definit prin ![]() ,
, ![]() ,
, ![]() . Sa se determine termenul general
. Sa se determine termenul general ![]() al sirului.
al sirului.
11. Calculati in functie de ![]() si
si ![]() suma
suma ![]() , daca
, daca ![]() este o progresie
geometrica de ratie
este o progresie
geometrica de ratie ![]() .
.
12. Aratati ca daca ![]() sunt sumele primilor
sunt sumele primilor ![]() teremeni,
teremeni, ![]() termeni si
respectiv
termeni si
respectiv ![]() termeni ai unei
progresii geometrice, atunci :
termeni ai unei
progresii geometrice, atunci :
![]() .
.
13. Sa se arate ca daca :
14. Daca ![]() este o progresie
aritmetica de ratie
este o progresie
aritmetica de ratie ![]() , atunci sa se calculeze sumele :
, atunci sa se calculeze sumele :
![]()
![]() in functie de
in functie de ![]() si
si ![]() .
.
15. Fie ![]() o progresie aritmetica.
Definim sirul
o progresie aritmetica.
Definim sirul ![]() prin
prin ![]() ,
, ![]() . Aratati ca
. Aratati ca ![]() este de asemenea o
progresie aritmetica.
este de asemenea o
progresie aritmetica.
16. Aratati ca numerele ![]() nu pot fi termenii
unei progresii aritmetice.
nu pot fi termenii
unei progresii aritmetice.
17. Se considera sirul ![]() definit prin
definit prin ![]() ,
, ![]() ,
, ![]() .
.
18. Daca ![]() ,
, ![]() reprezinta suma
primilor
reprezinta suma
primilor ![]() termeni ai
sirului
termeni ai
sirului ![]() , atunci :
, atunci :
a)
Sa se determine ![]() ;
;
b)
Sa se arate ca
sirul ![]() este o progresie
aritmetica.
este o progresie
aritmetica.
19. Calculati suma numerelor pare de doua cifre.
20. Sa se rezolve ecuatiile :
a)
![]() ;
;
b)
![]() ;
;
c)
![]() ;
;
d)
![]() ;
;
e)
![]() .
.
21. Progresiile aritmetice 17,21, 25, ![]() si
si ![]() au si termeni
comuni. Sa se arate ca suma primilor
au si termeni
comuni. Sa se arate ca suma primilor ![]() termeni comuni este
egala cu
termeni comuni este
egala cu ![]() .
.
22. Sa se determine ![]() astfel incat
sirul de numere
astfel incat
sirul de numere ![]() definit prin
definit prin ![]() si
si ![]() ,
, ![]() sa fie o
progresie aritmetica.
sa fie o
progresie aritmetica.
23. Sa se calculeze sumele :
a)
![]() ;
;
b)
![]() ;
;
c)
![]() ;
;
d) ![]() ;
;
e)
![]() ;
;
f)
![]() , si apoi aratati ca
, si apoi aratati ca ![]() ,
, ![]() ;
;
g)
![]() ,
, ![]() .
.
24. a) Aratati ca numarul ![]() este patrat
perfect.
este patrat
perfect.
b)
Demonstrati egalitatea : 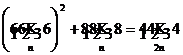 .
.
25. Determinati trei numere in progresie
geometrica daca suma lor este 26, iar suma inverselor lor este ![]() .
.
26. Determinati ![]() in progresie
geometrica, daca
in progresie
geometrica, daca ![]() si
si ![]() .
.
27. Determinati sase termeni in progresie geometrica daca suma primilor trei este egala cu 168, iar suma ultimilor trei este 21.
28. Deteminati patru numere in progresie geometrica daca suma termenilor extremi este 27, iar suma termenilor din mijloc este 18.
29. Unsprezece numere sunt in progresie aritmetica. Primul termen este 24. Daca primul, al cincilea si al unsprezecelea termen sunt in progresie geometrica, atunci determinati cei unsprezece termeni.
30. Trei numere sunt in progresie geometrica. Daca se aduna 8 la al doilea numar, atunci aceste numere sunt in progresie aritmetica. Daca apoi 64 se aduna la al treilea numar (din ultimele trei), atunci numerele obtinute sunt in progresie geometrica. Sa se determine cele trei numere.
31. Intr-o progresie aritmetica al doilea termen este medie geometrica intre primul si al patrulea termen. Aratati ca al patrulea, al saselea si al noualea termen sunt in progresie geometrica.
32. Determinati o progresie aritmetica si o progresie geometrica daca primul termen din fiecare este egal cu 2, al treilea termen in cele doua progresii este acelasi, iar al unsprezecelea teremen al progresiei aritmetice este egal cu al cincilea termen al progresiei geometrice.
33. Primul termen dintr-o progresie aritmetica si geometrica este egal cu 3. Al doilea termen al progresiei aritmetice este mai mare cu 6 decat al doilea termen al progresiei geometrice. Termenul al treilea din cele doua progresii este acelasi. Determinati aceste progresii.
34. Suma a trei numere in progresie aritmetica este egala cu 21. Daca 2, 3 si 9 se aduna acestor numere, atunci se obtin alte trei numere in progresie geometrica. Determinati cele trei numere.
35. Se dau patru numere in progresie geometrica. Daca la aceste numere se adauga 3, 9, 11 si respectiv1, atunci se obtin alte patru numere in progresie aritmetica. Determinati numerele initiale.
36. Daca ![]() sunt in progresie
geometrica, atunci :
sunt in progresie
geometrica, atunci :
a)
![]() ;
;
b)
![]() ;
;
c)
![]()
sunt de asemenea in progresie geometrica.
37. Fie sirul ![]() definit prin
definit prin ![]() ,
, ![]() ,
, ![]() .
.
Aratati ca sirul ![]() nu este o progresie
geometrica, dar sirul
nu este o progresie
geometrica, dar sirul ![]() cu
cu ![]() ,
, ![]() reprezinta o
progresie geometrica.
reprezinta o
progresie geometrica.
38. Aratati numerele ![]() nu pot fi teremenii
unei progresii geometrice.
nu pot fi teremenii
unei progresii geometrice.
39. Daca ![]() sunt
radacinile ecuatiei
sunt
radacinile ecuatiei ![]() , iar
, iar ![]() sunt
radacinile ecuatiei
sunt
radacinile ecuatiei ![]() . Numerele
. Numerele ![]() ,
,![]() sunt in progresie geometrica strict crescatoare.
Determinati pe
sunt in progresie geometrica strict crescatoare.
Determinati pe ![]() si
si ![]() .
.
40. a) Daca ![]() este suma primilor
este suma primilor ![]() termeni ai unei
progresii geometrice de ratie
termeni ai unei
progresii geometrice de ratie ![]() , atunci aratati ca
, atunci aratati ca ![]() ,
, ![]() .
.
b) Aratati ca :
![]() .
.
41. Se considera sirul ![]() definit prin
definit prin ![]() ,
, ![]() ,
, ![]() . Aratati ca sirul
. Aratati ca sirul ![]() ,
, ![]() este o progresie
geometrica si calculati
este o progresie
geometrica si calculati ![]() .
.
42. Fie sirurile ![]() ,
, ![]() definite prin
definite prin ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
a)
Aratati ca ![]() nu este progresie
geometrica ;
nu este progresie
geometrica ;
b)
Aratati ca ![]() este progresie
geometrica ;
este progresie
geometrica ;
c)
Determinati pe ![]() si
si ![]() in functie de
in functie de ![]() .
.
43. Sa se gaseasca suma
primilor douazeci de termeni ai unei progresii aritmetice, stiind
ca ![]() .
.
44. Sa se calculeze urmatoarele sume :
a)
![]() ;
;
b)
![]() , unde
, unde ![]() ,
, ![]() ,
, ![]() .
.
45. Sa se arateca daca ![]() sunt in progresie
geometrica atunci are loc relatia
sunt in progresie
geometrica atunci are loc relatia 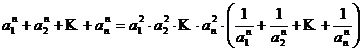 .
.
46. Daca ![]() sunt in progresie
aritmetica, sa se calculeze suma :
sunt in progresie
aritmetica, sa se calculeze suma :
![]() .
.
Sa se calculeze suma ![]() .
.
47. Sa se calculeze suma ![]() stiind ca
stiind ca ![]() sunt in progresie
aritmetica. Caz particular :
sunt in progresie
aritmetica. Caz particular : ![]() . Sa se calculeze
. Sa se calculeze
![]() .
.
48. Sa se calculeze urmatoarele sume :
a)
![]() ;
;
b)
![]() .
.
49. Daca ![]() sunt sumele primilor
sunt sumele primilor ![]() termenei din
termenei din ![]() progresii aritmetice
in care primul termen este 1 si ale caror ratii sunt
progresii aritmetice
in care primul termen este 1 si ale caror ratii sunt ![]() sa se arate
ca aceste sume formeaza o progresie aritmetica. Sa se arate
ca :
sa se arate
ca aceste sume formeaza o progresie aritmetica. Sa se arate
ca :
![]() .
.
50. Sa se determine termenul al ![]() -lea al unei progresii aritmetice
-lea al unei progresii aritmetice ![]() , daca
, daca ![]() si
si ![]() , unde
, unde ![]() .
.
51. Fie numerele pozitive ![]() in progresie
geometrica crescataore si
in progresie
geometrica crescataore si ![]() un numar natural
nenul. Sa se arate ca raportul sumelor
un numar natural
nenul. Sa se arate ca raportul sumelor
![]() si
si ![]() nu depinde de n.
nu depinde de n.
52. Sa se determine teremenul general al
sirului ![]() definit prin :
definit prin :
![]() si pentru orice
si pentru orice ![]() avem
avem ![]() .
.
53. Sa se calculeze sumele :
a)
![]() ;
;
b)
![]() ,
, ![]() fiind un numar
real.
fiind un numar
real.
54. Sa se calculeze suma
![]() .
.
55. Fie sirul de numere ![]() , unde
, unde ![]() ,
, ![]() si pentru orice
numar natural
si pentru orice
numar natural ![]() , avem :
, avem :
![]() . Sa se demonstreze ca
. Sa se demonstreze ca ![]() , oricare ar fi
, oricare ar fi ![]() .
.
56. Fie sirul de numere reale ![]() , unde
, unde ![]() ,
, ![]() si pentru orice
numar natural
si pentru orice
numar natural ![]() , avem
, avem ![]() . Sa se gaseasca formula termenului general.
. Sa se gaseasca formula termenului general.
57. Fie sirul de numere ![]() astfel incat
astfel incat ![]() si
si ![]() . Sa se gaseasca formula care defineste
termenul geberal.
. Sa se gaseasca formula care defineste
termenul geberal.
58. Fie sirul ![]() , definit astfel :
, definit astfel : ![]() si
si ![]() . Sa se demonstreze ca oricare ar fi
. Sa se demonstreze ca oricare ar fi ![]() , avem
, avem ![]() .
.
59. Fie ![]() suma primilor
suma primilor ![]() termeni ai
sirului :
termeni ai
sirului :
![]() .
.
a)
Sa se gaseasca o
formula pentru ![]() ;
;
b)
Sa se arate ca ![]() , unde
, unde ![]() sunt numere naturale
cu
sunt numere naturale
cu ![]() .
.
60. Fie ![]() si
si ![]() sirul definit
prin relatia
sirul definit
prin relatia ![]() . Fie
. Fie ![]() ,
, ![]()
![]() si
si ![]() ,
, ![]() radacinile
ecuatiei
radacinile
ecuatiei ![]() . Daca
. Daca ![]() , atunci
, atunci ![]() este de forma
este de forma
![]() , iar daca
, iar daca ![]() , atunci
, atunci ![]() este de forma
este de forma ![]() , unde
, unde ![]() si
si ![]() sunt numere reale.
sunt numere reale.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 10937
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved