| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
INDICII SI RITMUL VARIATIEI FENOMENELOR ECONOMICO-SOCIALE
Notiunea si importanta indicilor
Indicii simpli
Indicii de grup
Sistemul indicilor calculati din marimi medii
Gruparea indicilor dinamicii dupa felul bazei
Ritmul variatiei si al sporului
1. Notiunea si importanta indicilor
Indicii masoara variatia in timp si in spatiu a fenomenelor social economice in functie de modificarea factorilor de influienta.
Indicii reprezinta o categorie speciala a indicatorilor statistici cu ajutorul carora se masoara variatia medie relativa a fenomenelor economice si sociale.
Indicii se obtin prin raportarea a doua niveluri absolute ale aceluiasi fenomen sau grup de fenomene, in doua unitati diferite de timp si de spatiu.
Variatia in timp a fenomenelor si proceselor colective este redata cu ajutorul indicilor dinamicii.
Compararea nivelurilor atinse de o colectivitate data in teritorii diferite se realizeaza cu ajutorul indicilor teritoriali.
Indicii calitativi au rolul de a masura si caracteriza raportul dintre grupe calitative diferite ale unei colectivitati date.
Indiferent de categoria lor, indicii au o baza metodologica comuna. Aceasta consta in comparerea a doua niveluri diferite ale unui indicator statistic dat.
In calculul indicilor se porneste de la o serie statistica. Se stabileste un termen al seriei, de multe ori primul, sau din afara seriei avand o semnificatie in analiza, ca baza de comparatie si apoi se raporteaza in mod succesiv ceilalti termeni ai seriei la termenul de baza.
Valoarea raportului este numarul indice cautat, el exprimand variatia relativa a termenului raportat. Forma obisnuita de exprimare a indicilor este cea procentuala.
Variatia relativa ce se obtine in procesul determinarii indicilor poate fi privita sub doua aspecte :
-relativitatea bazei, acesta fiind aleasa in functie de problemele puse in analiza;
-felul marimilor ce rezulta din raportul a doi indicatori ai aceleiasi serii.
Aparitia indicilor este strans legata de necesitatea ce s-a simtit in economia mijlocului secolului al XIX-lea de a masura si caracteriza variatia curenta a pretului marfurilor si a cursului valorilor mobiliare cotate la bursa.
Prin aparitia si utilizarea a numerosi indici s-a impus clasificarea lor dupa diverse criterii :
Dupa sfera de cuprindere intalnim:
indici individuali, simpli sau elementari, masoara variatia relativa a unor fenomene simple, singulare, in timp sau in spatiu.
indici de grup, compusi sau sintetici, masoara variatia medie relativa a unor fenomene colective in raport cu o anumita baza de comparatie.
Dupa natura caracteristicii studiate, indicii sunt:
- indicii dinamicii, exprima variatia in timp,
- indicii teritoriali, exprima variatia in spatiu,
- indicii calitativi, exprima variatia unei caracteristici calitative.
Dupa modul de alegere a bazei se cunosc:
indicii cu baza fixa
indicii cu baza mobila.
Indicii de grup, la randul lor, se grupeaza dupa procedeul de calcul:
indici agregati,
indici calculati ca medii aritmetice ponderate a indicilor simpli,
indici calculati ca medii armonice ponderate a indicilor simpli,
indici calculati prin raportarea a doua medii aritmetice ponderate,
indici calculati sub forma de medie geometrica.
2. Indicii simpli
Exprima variatia unei colectivitati simple sub aspectul unei caracteristici date.
Indicatorii comparati pot fi cantitativi sau valorici, in functie de scopul urmarit in cercetare si de datele disponibile.
In primul caz se obtine un indice simplu cantitativ, iar in al doilea caz un indice simplu valoric.
Principalii indici simpli sunt:
Indicele simplu al cantitatilor
sau al volumului fizic care
este determinat dupa relatia: ![]() ,
,
q1 = volumul fizic in perioada curenta
q0 = volumul fizic in perioada de baza
Indicele simplu al preturilor stabilit astfel:
![]()
p1 = pretul in perioada curenta
p0 = pretul in perioada de baza
Indicele simplu valoric stabilit astfel:
![]() , dar v1=q1p1
, dar v1=q1p1
v0=q0p0
![]()
Intre acesti indici se verifica relatia:
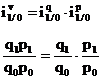
Indicii de grup
Sunt indici compusi ce masoara variatia unor colectivitati mai largi, in componenta carora intra doua sau mai multe colectivitati simple.
Deoarece elementele colectivtatilor simple care intra in studiul variatiei de grup nu pot fi insumate si nu pot fi comparate direct din cauza naturii lor diferite, ele se omogenizeaza sub un anumit aspect. Pentru aceasta se foloseste un factor de omogenizare, ca de ex. pretul in cazul bunurilor materiale.
In cadrul indicilor de grup aceasta unitate de omogenizare are rolul de pondere.
Dupa modul de calcul, indicii de grup sunt:
a. indicele agregat
b. indicele mediu aritmetic
c. indicele mediu armonic
a. Indicele agregat
Este forma generala a indicelui de grup. Se calculeaza ca raport intre suma marimilor absolute ale colectivitatilor partiale cuprinse in studiu, luate cu ponderi constante sau variabile.
Indicele agregat simplu al productiei se determina astfel:
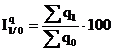
Pentru masurarea variatiei de grup a volumului fizic al unor produse se utilizeaza indicele agregat ponderat, calculat astfel:
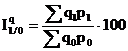
La construirea indicelui agregat ponderat se pot utiliza diferite sisteme de ponderare, si anume:
Sistemul de ponderare propus in 1864 de E. Laspeyres, la care ponderile folosite sunt cele din perioada de baza. Se foloseste pentru masurarea variatiei de grup a volumului fizic al unor produse, cantitatile respective fiind ponderate cu un pret constant, astfel:
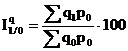
Sistemul de ponderare propus in 1874 de H. Paasche, la care ponderile folosite sunt cele din perioada curenta. Se foloseste pentru masurarea dinamicii pretului mediu pentru diferite produse, astfel:
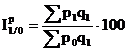
Pentru caracterizarea variatiei valorice a unui grup de produse se utilizeaza relatia indicelui agregat la care variaza, de la o perioada la alta, ambii factori, astfel:
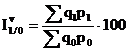
Intre acesti indici se verifica relatia:
![]()
In teoria indicilor se mai intalnesc si unele sisteme de ponderare care tin seama de ponderile din ambele perioade. Intalnim astfel:
-indicele preturilor calculat de Edgeworth, care se bazeaza pe acumularea cantitatilor din perioada de baza cu cele din perioada curenta si folosirea acestora ca pondere la masurarea variatiei relative a preturilor, dupa relatia:
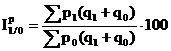
-indicele ideal al lui Fisher. Este un indice de grup al preturilor calculat ca o medie geometrica a celor doi indici agregati, de tip Laspeyres si Paasche, astfel:
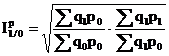
Acest indice se foloseste in special in calculul indicilor teritoriali pe plan international.
In practica tarilor dezvoltate, statistica utilizeaza sistemul propus de Laspeyres. Existenta mai multor sisteme de ponderare provine din faptul ca formulele de calcul propuse nu satisfac integral teoria si practica folosirii metodei indicilor.
Pe baza indicilor agregat se poate calcula influenta variatiei factorilor studiati in marimi absolute, sub forma diferentei dintre numaratorul si numitorul formulei indicelui respectiv.
In cazul indicelui de grup al volumului fizic, modificarea absoluta va fi:
![]()
Pentru indicele de grup al preturilor, modificarea absoluta va fi:
![]()
In cazul indicelui de grup valoric, modificarea este:
![]()
In cazul influentei factorilor exprimata in marimi absolute se verifica relatia:
![]()
Ex. Volumul productiei si preturile unitare pentru 4 produse in 1999 si 2002 la firma "X". S.A. sunt urmatoarele:
Tabelul 4 Elemente pentru determinarea indicilor agregati
|
Produsul si clasa de calitate |
Volumul productiei -tone |
Pretul -mii lei / tona- |
Valoarea productiei -mil lei- |
|||||
|
q0 |
q1 |
p0 |
p1 |
q0p0 |
q0p1 |
q1p0 |
q1p1 |
|
|
Tomate | ||||||||
|
Castraveti | ||||||||
|
Salata | ||||||||
|
Gulii | ||||||||
|
TOTAL | ||||||||
|
|
|
|
|
|||||
Sa se calculeze indicii individuali si indicii de grup ai volumului fizic, preturilor si volumului valoric.
Indicii individuali ai volumului fizic se calculeaza dupa relatia:
![]()
![]()
![]()
![]()
![]()
Pentru a calcula indicele de grup al volumului fizic al productiei se foloseste indicele tip Laspeyres cu ponderea din perioada de baza.
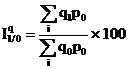
![]()
Modificarea absoluta a volumului fizic al productiei se determina cu ajutorul relatiei:
![]()
![]() mil. lei
mil. lei
Datele din tabelul prezentat sugereaza o schimbare a structurii.
Valoarea totala a ofertei in anul 2002 la pretul anului 1999 este de
3114,60 mil. lei (![]() ).
).
Pentru produsul "tomate", volumul fizic scade in anul 2002 fata de 1999 de 0,0908 ori. Exprimat in procente, volumul fizic a scazut in perioada curenta fata de perioada de baza cu 90,92%, adica la fiecare 100 tone realizate pentru produsul "tomate" in perioada de baza, se realizeaza 9,08 tone in perioada curenta.
Pentru produsul "castraveti" volumul fizic creste in 2002 fata de 1999 de 1,5179 ori. Exprimat in procente, volumul fizic a crescut in perioada curenta fata de perioada de baza cu 51,79%, adica la fiecare 100 tone realizate pentru produsul "castraveti" in 1999, se realizeaza 151,79 tone in 2002.
Pentru produsul "salata" volumul fizic creste in 2002 fata de 1999 de 2 ori. Exprimat in procente, volumul fizic a crescut in perioada curenta fata de perioada de baza cu 100,00%, adica la fiecare 100 tone realizate pentru produsul "salata" in 1999, se realizeaza 200 tone in 2002.
Pentru produsul "gulii", volumul fizic scade in anul 2002 fata de 1999 de 0,4074 ori. Exprimat in procente, volumul fizic a scazut in perioada curenta fata de perioada de baza cu 59,26%, adica la fiecare 100 tone realizate pentru produsul "gulii" in perioada de baza, se realizeaza 40,74 tone in perioada curenta.
Pe total produse, volumul fizic al productiei a scazut cu 33,12%.
Indicii individuali ai preturilor se calculeaza dupa relatia:
![]()
![]()
![]()
![]()
![]()
Indicele agregat al preturilor se determina ca un indice Paasche:
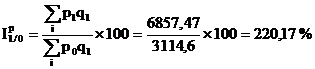
Indicii preturilor arata ca pentru produsul "tomate" pretul inregistreaza o crestere cu 107,14%, pentru produsul "castraveti" pretul creste cu 119,13%, pentru produsul "salata" pretul creste cu 214,99% si pentru produsul "gulii" pretul inregistreaza o crestere cu 14,43%.
Pe total produse, pretul unitar creste cu 120,17%.
Aportul acestei cai la cresterea globala este relevat prin calculul modificarii absolute a preturilor pe total produse, dupa relatia:
![]() mil. lei
mil. lei
Indicii individuali ai volumului valoric al productiei se calculeaza dupa relatia:
![]()
![]()
![]()
![]()
![]()
Indicile de grup (agregat) al volumului valoric se determina dupa relatia:
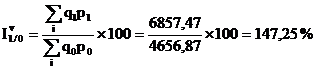
Indicii volumului valoric arata ca pentru produsul "tomate" volumul valoric inregistreaza o scadere cu 81,19%, pentru produsul "castraveti" volumul valoric creste cu 232,60%, pentru produsul "salata" volumul valoric creste cu 529,97%, iar pentru produsul "gulii" volumul valoric inregistreaza o scadere cu 53,38% . Pe total produse, volumul valoric creste cu 47,25%.
Modificarea absoluta a volumului valoric al productiei se determina dupa relatia:
![]() mil. lei
mil. lei
I. Relatiile dintre indici
Intre indicele volumului fizic, cel al preturilor si cel al volumului valoric exista urmatoarea relatie:
-pentru indici individuali: ![]()
-pentru produsul "tomate":
![]() sau 18,81%
sau 18,81%
-pentru produsul "castraveti":
![]() sau 332,6%
sau 332,6%
-pentru produsul "salata":
![]() sau 629,98%.
sau 629,98%.
-pentru indici de grup:
![]() sau
147,25%
sau
147,25%
b. Indicele mediu aritmetic ponderat
Este o forma transformata a indicelui agregat si se calculeaza ca o medie aritmetica a indicilor individuali ai fenomenului studiat, ponderati cu elementele de la numitorul formulei indicelui agregat corespunzator.
Atunci cand se cunosc indicii individuali ai volumului fizic pentru un grup de produse si valorile acestor produse din perioada de baza, dinamica volumului fizic al productiei pe total produse se poate calcula pe baza indicelui mediu aritmetic ponderat, astfel:
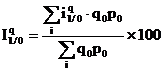
Ex. Intr-o unitate valoarea productiei in anul de baza si variatia volumului fizic al productiei, pe produse se prezinta astfel:
|
Produs |
Valoarea prod in per. de baza (mii lei) q0p0 |
Indicii individuali ai volumului fizic
|
|
A | ||
|
B | ||
|
C |
Sa se determine cresterea volumului fizic al productiei pe total produse.
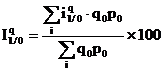
![]() %.
%.
c. Indicele mediu armonic ponderat
Se calculeaza ca o medie armonica a indicilor individuali ai fenomenului studiat, ponderati cu elementele de la numaratorul formulei indicelui agregat corespunzator. Se utilizeaza pentru studierea dinamicii preturilor pe total produse, atunci cand se cunosc indicii individuali ai preturilor si valoarea productiei din perioada curenta. Relatia de calcul:
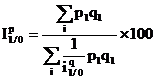
|
Produs |
Volumul valoric al prod in per. de curenta (mii lei) q1p1 |
Indicii individuali ai preturilor
|
|
A | ||
|
B | ||
|
C |
Sa se calculeze dinamica preturilor pe total produse.
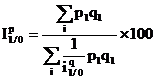
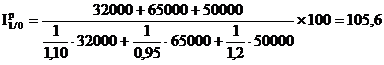 %
%
Sistemul indicilor calculati din marimi medii
Indicii se calculeaza nu numai din marimi absolute, ci si din marimi relative si medii. Atunci cand in calculul indicilor de grup se compara marimi medii, putem obtine, in functie de modul in care sunt combinate elementele cuprinse in calcul trei categorii de indici, avand functii analitice diferite.
Prin sistemul acestor indici se efectueaza analiza factoriala a variatiei colectivitatilor sau fenomenelor social-economice.
Cu ajutorul lor se pot masura influentele globale sau izolate ale factorilor care au intervenit direct in variatia fenomenului social dat.
Completandu-se reciproc in analiza statistica, acest grup de indici constituie un sistem din care fac parte:
A. indicele de variatie bifactoriala;
B. indicele cu structura fixa;
C. indicele schimbarii structurii.
A. indicele de variatie bifactoriala
Este un indice de grup care arata variatia medie totala a unui fenomen produsa sub influenta directa a doi factori:
-variatia nivelului caracteristicii in fiecare grupa, ca factor esential al variatiei de ansamblu;
-variatia structurii sau ponderii grupelor in colectivitatea totala.
Denumit si indice cu structura variabila (Is.v), indicele de variatie bifactoriala este un raport intre doua medii cu ponderi diferite.
Pornind de la formula mediei
aritmetice ponderate: 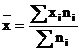 si aplicand regula de calcul a indicilor calculati
de marimi medii, obtinem:
si aplicand regula de calcul a indicilor calculati
de marimi medii, obtinem:
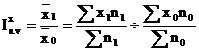
Formula se poate particulariza la diferite fenomene analizate in mod curent de statistica.
B. indicele cu structura fixa (Is.f)
Daca in cazul indicilor calculati din marimi medii, consideram ca ponderea grupelor care compun colectivitatea totala ramane neschimbata de la o perioada la alta, fie ea n1 sau n0, avem ceea ce se numeste indice cu structura sau pondere fixa.
Daca se aplica sistemul de ponderare propus de Paasche, indicele se construieste folosind ponderile din perioada curenta.
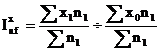
Daca indicele cu structura fixa se calculeaza folosind ponderile din perioada de baza, corespunde sistemului de ponderare propus de Laspeyres si formula devine:
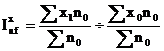
C. indicele variatiei structurii (Iv.s.).
Denumit si indicele modificarilor structurale, se calculeaza pornind de la ipoteza ca s-a schimbat numai distributia factorului cantitativ, deci structura colectivitatii.
Formula generala a acetui indice este cea aplicata in practica in care ponderarea se face cu datele perioadei de baza, de tip Laspeyres, astfel:
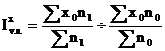
Intre aceste trei categorii de indici se stabileste relatia:
![]()
Ex. Presupunem urmatoarele date privind salariul mediu saptamanal (mii lei) si numarul de salariati din 3 sectii ale unei unitati:
|
Sectia |
Sal. mediu sapt. |
Nr. sal. |
|
|
|
||
|
|
|
n0 |
n1 |
||||
|
I | |||||||
|
II | |||||||
|
III | |||||||
|
Total | |||||||
Sa se determine dinamica salariului mediu pe total unitate.
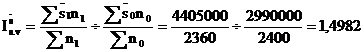 sau 149,82%.
sau 149,82%.
Pe total sectii, salariul mediu
a crescut in perioada curenta fata de perioada de baza de
1,4982 ori sau cu 149,82% sub influenta ambilor factori (![]() , n
, n
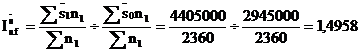 sau 149,58%.
sau 149,58%.
Salariul mediu a crescut de 1,4982 ori sau cu 149,82% sub influenta modificarii salariului mediu saptamanal pe fiecare sectie.
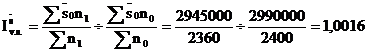 sau 100,16%.
sau 100,16%.
Pe total sectii, salariul mediu a crescut 1,0016 ori sau cu 100,16% ca urmare a modificarii numarului de salariati.
Relatii intre indici:
![]() ,
, ![]()
Gruparea indicilor dinamicii dupa felul bazei
Orice indice se exprima ca un raport intre 2 indicatori, dintre care unul este considerat ca baza de raportare, iar celalalt este marimea raportata.
Baza de raportare se poate alege dupa criterii diferite. La seriile de timp, se considera, de regula, primul termen al seriei. Se poate alege orice alt termen al seriei sau un nivel exterior seriei daca este semnificativ.
Indicii dinamicii, dupa felul bazei sunt:
a. Indici cu baza fixa - se obtin prin raportarea tuturor nivelurilor seriei la termenul ales drept baza de raportare.
Pp. ca in cazul volumului fizic avem seria: q0, q1,,qn-1, qn, iar q0 este baza de raportare. Indicii cu baza fixa sunt:
![]() ,
, ![]() , . ,
, . , ![]() ,
, ![]()
b. Indici cu baza fixa - se obtin prin raportarea tuturor nivelurilor seriei la termenul precedent. Considerand aceeasi serie, indicii cu baza mobila vor fi:
![]() ,
, ![]() , . ,
, . , ![]() ,
, ![]()
Intre aceste 2 categorii de indici se verifica relatiile:
-produsul indicilor cu baza mobila da indicele cu baza fixa corespunzator ultimului termen al seriei date:
![]()
-impartind doi indici cu baza fixa obtinem indicele cu baza mobila corespunzator:
![]()
Prin analiza comparativa a continutului indicilor cu baza fixa cu cel al indicilor cu baza mobila se pot face urmatoarele constatari:
-indicii cu baza fixa prezinta avantajul comparabilitatii de continut, unitatea de masura ramanand aceeasi. In cazul indicilor in lant, termenul de baza schimbandu-se, se schimba si valoarea unitatii care exprima variatia.
-indicii cu baza fixa nu sunt concludenti daca se raporteaza la o baza invechita. In acest caz trebuie sa se procedeze la actualizarea bazei pentru a permite analiza corecta a fiecarei etape.
Prin modificarea bazei de raportare a indicilor cu baza fixa la anumite perioade, acesti indici se apropie, intr-un fel sau altul, de metoda si functia aplicativa a indicilor in lant.
Ex. Productia unei firme intr-o perioada de 7 ani a evoluat astfel:
|
Anii |
Prod. (mii buc.) |
Sa se studieze dinamica productiei cu ajutorul indicilor grupati dupa felul bazei.
-indicii cu baza fixa:
![]()
![]() sau 84% ;
sau 84% ; ![]() sau 74%
sau 74%
![]() sau 93% ;
sau 93% ; ![]() sau 86%
sau 86%
![]() sau 88% ;
sau 88% ; ![]() sau 117%
sau 117%
-indicii cu baza mobila:
![]()
![]() sau 84% ;
sau 84% ; ![]() sau 88%
sau 88%
![]() sau 125,67% ;
sau 125,67% ; ![]() sau 92,4%
sau 92,4%
![]() sau 102,32% ;
sau 102,32% ; ![]() sau 132,95%
sau 132,95%
Relatii intre acesti indici:
-produsul
indicilor cu baza mobila da indicele cu baza fixa
corespunzator ultimului an: ![]()
-raportul a doi indici cu baza fixa da indicele cu baza mobila corespunzator:
![]()
Ritmul variatiei si al sporului
Analiza variatiei in timp a fenomenelor sociale este completata cu metoda ritmurilor. Ritmurile isi au punctul de plecare in indicii dinamicii, continutul lor confundandu-se pana la un punct cu al acestora. Metoda lor poate fi privita ca o prelungire a indicilor dinamicii in directia cunoasterii si caracterizarii fenomenelor sociale in evolutia lor timp.
Indicatorii care se pot utiliza in caracterizarea seriilor dinamice se grupeaza astfel:
Cuprind sporul absolut, care, dupa modul de alegere a bazei, este:
spor absolut cu baza fixa (![]() ) - se obtine ca diferenta intre fiecare
termen al sumei si termenul ales drept baza de raportare. Considerand
seria: x0, x1, x2, , xn, sporul
absolut cu baza fixa se va calcula astfel:
) - se obtine ca diferenta intre fiecare
termen al sumei si termenul ales drept baza de raportare. Considerand
seria: x0, x1, x2, , xn, sporul
absolut cu baza fixa se va calcula astfel:
![]() ;
; ![]() ; ..;
; ..; ![]() sau generalizand:
sau generalizand: ![]()
spor absolut cu baza mobila (![]() ) - este diferenta dintre fiecare termen al seriei
si termenul anterior. In aceeasi serie vom avea:
) - este diferenta dintre fiecare termen al seriei
si termenul anterior. In aceeasi serie vom avea:
![]() ;
; ![]() ; ..;
; ..; ![]() sau generalizand:
sau generalizand: ![]()
Intre sporurile absolute cu baza fixa si cele cu baza mobila se verifica relatiile:
-suma sporurilor cu baza mobila este sporul cu baza fixa al ultimului an:
![]()
-diferenta dintre doua sporuri absolute cu baza fixa consecutive este egala cu sporul cu baza mobila corespunzator:
![]()
Indicatorii relativi de masurare a variatiei in timp cuprind:
ritmul variatiei
ritmul sporului
Ritmul variatiei (Rx) - exprima viteza de variatie exprimata in marimi relative. Dupa modul de calcul, rimul variatiei este de doua feluri:
Ritmul variatiei cu
baza fixa (![]() ) - arata de cate ori a crescut sau scazut nivelul
unui fenomen in decursul unei perioade de timp si se calculeaza
astfel:
) - arata de cate ori a crescut sau scazut nivelul
unui fenomen in decursul unei perioade de timp si se calculeaza
astfel:
![]() ,
, ![]()
Ritmul variatiei cu
baza mobila (![]() ) - arata de cate ori a crescut sau scazut nivelul
unui fenomen intr-un moment fata de momentul anterior.
) - arata de cate ori a crescut sau scazut nivelul
unui fenomen intr-un moment fata de momentul anterior.
![]()
Intre ritmul variatiei cu baza fixa si cel cu baza mobila se verifica relatiile:
-produsul ritmurilor cu baza mobila este ritmul cu baza fixa al intregii perioade:
![]()
-raportul a doua ritmuri ale variabilei cu baza fixa este egal cu ritmul cu baza mobila corespunzator:
![]()
2 Ritmul sporului (rx) - exprima marimea cresterii sau scaderii in decursul unei anumite perioade de timp fata de perioada de baza a unui indicator. Se calculeaza:
Ritmul sporului cu baza
fixa (![]() ) - se calculeaza ca raport intre sporul cu baza
fixa si nivelul fenomenului considerat din perioada de baza,
astfel:
) - se calculeaza ca raport intre sporul cu baza
fixa si nivelul fenomenului considerat din perioada de baza,
astfel:
![]()
Ritmul sporului cu baza
mobila (![]() ) - se calculeaza ca raport intre sporul cu baza
mobila si nivelul fenomenului considerat din perioada
anterioara, astfel:
) - se calculeaza ca raport intre sporul cu baza
mobila si nivelul fenomenului considerat din perioada
anterioara, astfel:
![]()
Relatii intre aceste ritmuri:
-ritmul sporului este egal cu ritmul variatiei minus 1 sau 100, in functie de modul de exprimare a acestor ritmuri:
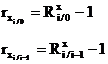
Indicatorii medii ai cresterii seriilor dinamice sunt:
1. Sporul mediu (![]() ) - se calculeaza ca o medie aritmetica
simpla a sporurilor absolute cu baza mobila. Cum suma
sporurilor cu baza mobila este sporul cu baza fixa a
ultimei perioade, atunci sporul mediu se va calcula astfel:
) - se calculeaza ca o medie aritmetica
simpla a sporurilor absolute cu baza mobila. Cum suma
sporurilor cu baza mobila este sporul cu baza fixa a
ultimei perioade, atunci sporul mediu se va calcula astfel:
![]() , unde:
, unde:
xn = ultimul termen al seriei,
x0 = primul termen al seriei,
n = nr. termenilor seriei.
2. Ritmul mediu al variatiei (![]() ) - exprima viteza medie relativa de crestere
a unui fenomen in decursul unei perioade de timp. Se determina prin
diverse metode, cea mai utilizata fiind metoda mediei geometrice,
astfel:
) - exprima viteza medie relativa de crestere
a unui fenomen in decursul unei perioade de timp. Se determina prin
diverse metode, cea mai utilizata fiind metoda mediei geometrice,
astfel:
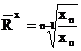
3. Ritmul mediu al sporului (![]() ) - se determina pe baza ritmurilor medii ale variatiei
astfel:
) - se determina pe baza ritmurilor medii ale variatiei
astfel:
![]() sau in procente:
sau in procente: ![]()
Ritmul mediu al sporului arata cu cat a crescut in medie in fiecare an al perioadei luate in calcul nivelul unui anumit fenomen.
Ex. Presupunem urmatoarea evolutie a productiei unei firme:
|
Anii |
Prod. (mii t) |
Sa se calculeze indicatorii absoluti, relativi si medii ai dinamicii.
Indicatorii absoluti:
Sporul absolut:
Sporul absolut cu baza
fixa: ![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]()
Sporul absolut cu baza
mobila: ![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]()
Relatiile dintre aceste sporuri:
-suma sporurilor cu baza mobila este sporul cu baza fixa al ultimului an:
![]()
-diferenta dintre doua sporuri absolute cu baza fixa consecutive este egala cu sporul cu baza mobila corespunzator:
![]()
Indicatorii relativi:
Ritmul variatiei:
Ritmul variatiei cu
baza fixa ![]()
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Ritmul variatiei cu
baza mobila ![]()
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Relatii intre ritmurile variatiei:
-produsul ritmurilor cu baza mobila este ritmul cu baza fixa al ultimului an:
![]()
-raportul a doua ritmuri ale variabilei cu baza fixa este egal cu ritmul cu baza mobila corespunzator:
![]()
Ritmul sporului:
Ritmul sporului cu baza
fixa: ![]()
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Ritmul sporului cu baza
mobila: ![]()
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Indicatorii medii:
Sporul mediu: ![]()
Ritmul mediu al variatiei: 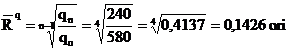
Ritmul mediu al sporului: ![]() ;
; ![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3126
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved