| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Proprietatile cifrei
Unele particularitati ale operatiilor artimetice cu numere intregi sunt legate de cifra 9. Orice proprietate a cifrei 9 pe care ati sesizat-o poate servi ca pretext pentru cele mai variate distractii matematice.
Cunoasteti, de pilda, regula divizibilitatii cu 9: un numar se imparte la 9 daca suma cifrelor din care este compus se imparte la 9. De aici rezulta ca suma cifrelor produsului oricarui numar cu 9 este egala cu noua sau cu un multiplu al lui (adica se divide cu 9).
De pilda, 354 x 9 = 3186, atunci 3 + 1 + 8 + 6 = 18 (se imparte la 9). De aceea, cand un elev din clasa intai se plangea ca ii vine greu sa memoreze tabla inmultirii primelor zece numere cu 9, tatal lui i-a recomandat o metoda simpla, aceea de a-si ajuta memoria cu degetele de la mana. Iata aceasta metoda
Prin miscarea unui deget. Asezati ambele maini pe masa si intindeti degetele. Fiecare deget de la stanga la dreapta va reprezenta numarul ordinal corespunzator: primul din stanga - 1, al doilea - 2, al treilea - 3, al patrulea - 4, al zecelea - 10. Avem de inmultit, de pilda, oricare din primele zece numere cu 9. Pentru aceasta este suficient, fara sa ridicati mainile de pe masa, sa ridicati degetul care reprezinta deinmultitul. Atunci numarul degetelor aflate in stanga celui ridicat va reprezenta numarul zecilor din produs, iar numarul degetelor din dreapta lui - numarul unitatilor.
Exemplu: avem de inmultit 7 cu 9. Asezati mainile pe masa si ridicati al saptelea deget; in stanga degetului ridicat se afla 6 degete, iar in dreapta 3. Asadar rezultatul inmultirii lui 7 cu 9 este 63.
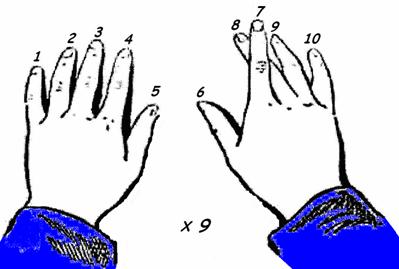
Aceasta inmultire mecanica, uimitoare la prima vedere, va deveni limpede indata ce ne vom reaminti ca suma cifrelor fiecarui produs din tabla inmultirii cu 9 este egal cu 9, iar numarul zecilor din produs este intotdeauna mai mic cu 1 decat numerele pe care le inmultim cu 9. Prin ridicarea degetului corespunzator subliniem tocmai acest lucru, si prin urmare inmultim.
Mana omului este una din primele masini de calculat.
Alte proprietati. Iata alte cateva proprietati interesante si utile pentru viitor, in legatura cu cifra 9.
1. Se imparte intotdeauna la 9:
a) diferenta dintre orice numar si suma cifrelor lui;
b) diferenta dintre doua numere cu cifre identice, dar asezate in mod diferit;
c) diferenta dintre doua numere care au suma cifrelor identica
2. Daca din oricare cifre sunt compuse numere ce se deosebesc doar prin ordinea succesiunii cifrelor, atunci la impartirea cu 9 a fiecaruia din ele ramane acelasi rest. El este egal cu restul impartirii la 9 a sumei cifrelor oricaruia din numerele respective.
Daca vom denumi prisos restul ramas din impartirea sumei cifrelor unui numar la 9, atunci:
a) prisosul sumei/diferentei numerelor este egal cu prisosul sumei/diferentei sumei prisosurilor termenilor;
b) prisosul produsului a doua numere este egal cu prisosul produsului prisosurilor numerelor date.
Puteti verifica cu usurinta aceste proprietati prin exemple numerice, iar daca stiti algebra puteti sa le si demonstrati. Dupa ce v-ati dumerit asupra rezolvarii problemelor din acest capitol, puteti folosi multe din ele ca trucuri matematice.
1. Care cifra a fost stearsa
Problema 1. Rugati un prieten sa scrie, fara sa va arate, un numar format din trei sau mai multe cifre, sa-l imparta la 9 si sa va spuna restul ramas. Apoi propuneti-i sa stearga din numarul ales de el o singura cifra (oricare); numarul format dupa stergerea cifrei sa-l imparta iarasi la 9 si sa va spuna din nou restul acestei impartiri. Veti putea indica imediat cifra care a fost stearsa, calauzindu-va dupa urmatoarele reguli:
a) daca al doilea rest este mai mic decat primul, atunci, scazand din primul rest pe cel de-al doilea, veti obtine tocmai cifra stearsa
b) daca al doilea rest este mai mare decat primul, atunci cifra stearsa o veti obtine scazand al doilea rest din primul marit cu 9;
c) daca resturile sunt egale, atunci cifra stearsa este fie 9, fie 0.
Stiti de ce?
Problema 2. Propuneti acum prietenului sa se gandeasca la doua numere cu cifre identice, dar asezate in ordine diferita si sa scada pe cel mai mic din cel mai mare. Fireste ca nu trebuie sa va comunice nici numerele alese, nici diferenta obtinuta. Cereti-i insa sa stearga una din cifrele diferentei (in afara de 0) si sa va spuna suma cifrelor ramase. Pentru a numi cifra stearsa este suficient sa completati numarul comunicat pana la cel mai apropiat multiplu al lui 9.
De exemplu: 72.105 - 25.071 = 47.034. Stergem cifra 3. Suma cifrelor ramase: 4 + 7 + 4 = 15. Completarea numarului 15 pana la cel mai apropiat multiplu al lui 9, adica 18, este egala cu 3, care ne da tocmai cifra stearsa
Care este explicatia?
Observatie. Problema poate fi variata in diferite chipuri, bazandu-ne pe proprietatile aratate mai sus ale numarului 9. De pilda, se poate propune sa se scada din numarul dat suma cifrelor lui, sa se stearga o cifra din diferenta in afara de 0 si 9) si sa se indice suma cifrelor ramase. Pentru ghicirea cifrei sterse folosim aceeasi metoda
Problema 3. Scriem un numar oarecare, de pilda 7.146. Stergem o cifra, de pilda 4. Din numarul ramas (care are o cifra mai putin) scadem suma cifrelor numarului initial (18). In exemplul nostru vom obtine: 716 - 18 = 698. Rezultatul se anunta
Cum se poate afla cifra stearsa, cunoscand rezultatul scaderii?
Problema 4. Scrieti doua sau mai multe numere cu acelasi numar de cifre. Voi adauga tot atatea numere si ma voi indeparta, rugandu-va sa stergeti orice cifra doriti, in afara de zero, si sa faceti adunarea numerelor ramase. Daca imi veti comunica suma sau macar suma cifrelor sumei, va voi spune imediat care cifra a fost stearsa. De exemplu:

Suma cifrelor sumei 1 + 2 + 9 + 8 = 20. Este stearsa cifra 7.
Cum am ales numerele pe care le-am adaugat eu si cum se poate afla cifra stearsa
Problema 5. In problema precedenta se recomanda sa se adauge tot atatea numere cate au fost scrise de cel care a ales primele cifre. Dar in aceleasi conditii ne putem limita numai la adaugarea unui singur numar. De exemplu:
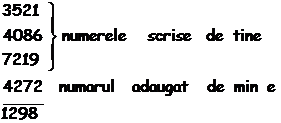
Suma cifrelor sumei 1 + 9 + 1 + 8 = 19. A fost stearsa cifra 8.
Ce numar trebuie sa adaug in acest caz si cum pot afla cifra stearsa
Problema 6. Aceeasi idee poate fi exprimata si altfel. Propuneti sa se scrie alaturi cateva coloane de numere cu o singura cifra, iar dumneavoastra adaugati in dreapta sau in stanga - dupa dorinta partenerului - inca o coloana de numere, in asa fel ca fiecare numar adaugat sa completeze suma numerelor dintr-un rand pana la un multiplu al lui 9.
Acum puteti, fara teama, sa propuneti partenerului sa stearga o cifra oarecare, sa adune numerele ramase dupa regula adunarii numerelor cu mai multe cifre si sa va comunice suma rezultata. Afland suma cifrelor rezultatului si folosind regula cunoscuta, puteti preciza lesne cifra stearsa. De exemplu:

Suma cifrelor sumei, fara
S-a sters cifra 4. E interesant ca in loc sa adaugati o coloana de numere va puteti margini la un singur numar de o cifra, adaugat in oricare loc.
Aflati cum se poate realiza aceasta.
2. O insusire ascunsa
Numarul 1.313 se memoreaza usor; de aceea, cel care vrea sa demonstreze prietenilor sai un truc cu o cifra stearsa poate manipula usor cu el. Pentru aceasta, propuneti prietenilor vostri sa scrie numarul 1.313 si sa scada din el un numar pe care il indicati.
Pentru scadere puteti indica orice numar: fiecarui participant - altul. Apoi fiecare din ei trebuie sa adauge in stanga sau in dreapta numarului obtinut dupa scadere (fiti atenti: nu aduna, ci adauga) numarul pe care l-a scazut, dar marit cu 100, iar din numarul rezultat sa stearga orice cifra in afara de zero, comunicandu-va cifrele ramase. Cu ajutorul acestor cifre puteti preciza cu usurinta cifra stearsa
Care din particularitatile numarului 1.313, legata de proprietatea cifrei 9, ne ajuta sa numim cifra stearsa si cum se poate face acest lucru?
3. Alte cateva metode distractive pentru gasirea cifrei care lipseste
Problema 1. Din noua cifre 1, 2, 3, 4, 5, 6, 7, 8 si 9 aleg opt si le scriu la intamplare, fara nici o ordine, pe o foaie de hartie. Pentru a nu va arata ce cifre am ales, le-am inlocuit in figura cu cerculete. Dedesubtul cifrelor trag dreapta AB si o denumesc dreapta sumelor". Apoi reunesc cifrele la intamplare prin cateva linii drepte sau frante - la alegerea mea - dar iau fiecare cifra numai o singura data
Sub drepta sumelor" notez suma cifrelor aflate de-a lungul fiecarei linii si va arat numai numerele care au fost obtinute sub dreapta sumelor" sau va spun suma cifrelor lor.
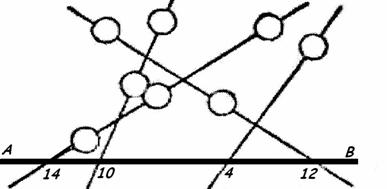
Numerele notate sub dreapta sumelor" ne dau urmatoarea suma a cifrelor:
Cunoscand numai acest numar, stabiliti care cifra din cele 9 alese initial n-a fost folosita
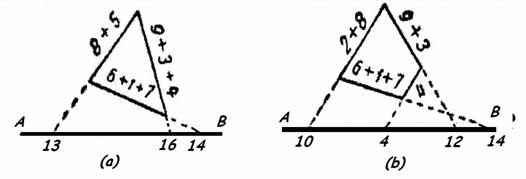
Observatie! In loc sa imprastii cifrele alese pe foaia de hartie, le pot scrie, in ordinea pe care o doresc, de-a lungul laturilor unui triunghi desenat dinainte (a), ale unui patrulater (b) sau ale unui poligon, si sub dreapta sumelor" sa scriu suma cifrelor asezate de-a lungul fiecarei laturi a figurii alese.
Problema 2. Acum scriu la intamplare pe o foaie de hartie numerele 11, 22, 33, 44, 55, 66, 77, 88, 99. Trag din nou dreapta sumelor" si reunesc prin cateva linii toate cifrele numerelor, in afara de una - cea aleasa in asa fel incat fiecare cifra - sa fie taiata numai de o singura linie. Pentru a nu va arata cifra pe care am ales-o in figura urmatoare fiecare numar este inlocuit cu un dreptunghi cu doua despartituri, corespunzatoare cifrelor numarului respectiv.
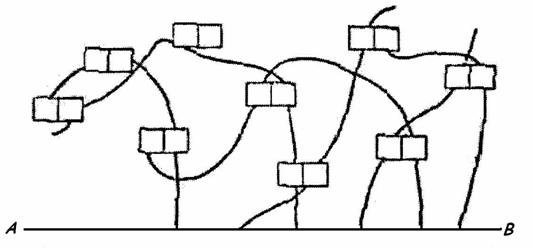
Notez sub dreapta sumelor" sumele cifrelor din care sunt alcatuite numerele situate de-a lungul fiecarei linii si va rog din nou sa stabiliti pe baza lor cifra omisa. Cei care au inteles problema precedenta o vor rezolva lesne si pe aceasta.
Problema 3. Scrieti toate numerele ordinale de la 1 la 8 si alegeti unul. Restul de sapte numere aranjati-le cum doriti, in doua sau mai multe coloane. Adunati toate numerele, considerandu-le numere cu mai multe cifre, si comunicati-mi suma lor sau suma cifrelor care formeaza suma. Voi stabili cu repeziciune numarul pe care l-ati ales.
Cum procedez?
4. Pe baza unei cifre din rezultat se stabilesc celelalte trei
Un numar oarecare format din doua cifre identice a fost inmultit cu 99. E lesne de inteles ca produsul va fi un numar cu patru cifre. S-a pastrat insa numai o singura cifra din rezultat, a treia.
Cum se poate stabili intreg produsul, cunoscandu-se aceasta unica cifra? Sa admitem ca cifra care s-a pastrat este 5.
Care este produsul?
5. Ghicirea diferentei
Fara sa-mi aratati, scrieti un numar de trei cifre, diferite la extremitati (sa presupunem 621), si formati un alt numar din aceleasi cifre, dispuse insa in ordine inversa (pentru exemplul dat - 126). Calculati diferenta lor, scazand numarul mai mic din cel mare (621 - 126 = 495) si comunicati-mi ultima cifra a diferentei (5), iar eu va voi spune rezultatul intreg.
Cum procedez?
6. Stabilirea varstei
Daca inversati cifrele varstei lui A, obtineti varsta lui B. Diferenta intre varsta lui A si B da varsta indoita a lui C, iar B este de 10 ori mai in varsta decat C.
Care este varsta fiecaruia?
7. Care-i secretul?
Unul dintre prietenii mei a declarat intr-o societate ca este in stare, fara sa se gandeasca prea mult, sa scrie oricate numere formate dintr-un numar fara sot de cifre, si fiecare din ele va avea urmatoarea insusire uimitoare: daca se aduna toate cifrele numarului scris, apoi se aduna toate cifrele sumei obtinute si asa mai departe, pana cand suma cifrelor va fi reprezentata printr-o singura cifra, atunci aceasta cifra va fi identica cu cifra aflata exact in mijlocul numarului initial.
El ne-a dat o sumedenie de exemple de asemenea numere. Printre ele erau unele cu trei cifre, de pilda 435, altele cu cinci cifre 46.853, si chiar cu 13 cifre, de exemplu 1.207.941.800.554. El a scris si numere care contineau cifre indicate de noi Si toate aveau proprietatea pe care o enuntase.
Sa verificam chiar numerele date ca exemplu. Avem:
Dupa cum vedeti, suma finala a cifrelor indica de fiecare data cifra de la mijiocul numarului. Talentul" original al prietenului meu ne-a produs o impresie puternica. Era limpede ca nu putuse memora atatea numere! Am incercat si noi sa scriem la noroc numere similare, dar foarte rar s-a intamplat sa aiba insusirea de mai sus.
Care este secretul numerelor scrise de prietenul meu?
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2126
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved