| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Relatii binare
Definitie. Fie ![]() si
si ![]() doua
multimi. O submultime
doua
multimi. O submultime ![]() se numeste relatie (uneori relatie binara) intre
elementele lui
se numeste relatie (uneori relatie binara) intre
elementele lui ![]() si elementele lui
si elementele lui
![]() . In cazul particular cand
. In cazul particular cand ![]() , o relatie
, o relatie ![]() se numeste
relatie pe
se numeste
relatie pe ![]() .
.
Sa consideram o relatie ![]() . Pentru o pereche ordonata
. Pentru o pereche ordonata ![]() , putem avea
, putem avea ![]() sau
sau ![]() . In primul caz scriem
. In primul caz scriem ![]() si citim "
si citim "![]() este in relatia
este in relatia ![]() cu
cu ![]() " iar in al doilea caz scriem
" iar in al doilea caz scriem ![]() (
(![]() nu este in relatia
nu este in relatia ![]() cu
cu ![]() ) .
) .
Definitie. O
relatie ![]() pe multimea
pe multimea ![]() se numeste reflexiva daca
se numeste reflexiva daca
![]() ,
,
simetrica daca
![]()
si tranzitiva daca
![]() si
si ![]() .
.
Definitie. Relatia
![]() se numeste relatie de echivalenta
daca este simetrica, reflexiva si tranzitiva.
se numeste relatie de echivalenta
daca este simetrica, reflexiva si tranzitiva.
Exemplu
Relatia
de egalitate. Relatia de egalitate ![]() este evident o
relatie de echivalenta pe multimea
este evident o
relatie de echivalenta pe multimea ![]() .
.
Legi de compozitie
Definitie. Fie ![]() o multime
nevida. O aplicatie
o multime
nevida. O aplicatie ![]() definita pe
produsul cartezian
definita pe
produsul cartezian ![]() cu valori in
cu valori in ![]() ,
, ![]() ,
, ![]() se numeste lege de compozitie.
se numeste lege de compozitie.
Observatie.
Elementul unic determinat ![]() care corespunde
perechii ordonate
care corespunde
perechii ordonate ![]() prin aplicatia
prin aplicatia ![]() se numeste compusul lui
se numeste compusul lui ![]() cu
cu ![]() prin legea de
compozitie
prin legea de
compozitie ![]() .
.
Observatie. Legile de compozitie sunt date prin diverse notatii, de exemplu :
![]() , etc.
, etc.
Exemple
1. Adunarea
si inmutirea matricilor. Fie ![]() multimea tuturor
matricilor patratice de ordin 2 cu coeficienti din
multimea tuturor
matricilor patratice de ordin 2 cu coeficienti din ![]() .
.
Asociind
fiecarei perechi ordonate ![]() de matrice din
de matrice din ![]() matricea
matricea ![]() se obtine o lege
de compozitie
se obtine o lege
de compozitie ![]() pe
pe ![]() ,
,
![]() ,
,
numita operatia de adunare a matricelor.
Asociind
fiecarei perechi ordonate ![]() de matrice din
de matrice din ![]() matricea
matricea
![]() se obtine o lege
de compozitie
se obtine o lege
de compozitie ![]() pe
pe ![]() ,
,
![]() ,
,
numita operatia de inmultire a matricelor.
2. Compunerea
functiilor. Fie ![]() o multime si
o multime si
![]() multimea tuturor
functiilor
multimea tuturor
functiilor ![]() . Asociind fiecarei perechi ordonate
. Asociind fiecarei perechi ordonate ![]() de functii din
de functii din ![]() functia
functia ![]() se obtine o lege
de compozitie
se obtine o lege
de compozitie ![]() pe
pe ![]() ,
,
![]() ,
,
numita operatia de compunere a functiilor.
Tabla unei legi de compozitie
Fie
![]() o multime
finita,
o multime
finita, ![]() . In acest caz o lege de compozitie
. In acest caz o lege de compozitie ![]() pe
pe ![]() ,
, ![]() , poate fi data prin ceea ce este cunoscut sub numele de
tabla operatiei
, poate fi data prin ceea ce este cunoscut sub numele de
tabla operatiei ![]() , care consta dintr-un tabel cu
, care consta dintr-un tabel cu ![]() linii si
linii si ![]() coloane afectate celor
coloane afectate celor
![]() elemente ale lui
elemente ale lui ![]() . Tabla legii de compozitie
. Tabla legii de compozitie ![]() contine la
intersectia liniei lui
contine la
intersectia liniei lui ![]() cu coloana lui
cu coloana lui ![]() , elementul
, elementul ![]() .
.
|
|
|
|
|
| ||
|
|
||
Exemplu
Se considera multimea ![]() si legea de
compozitie
si legea de
compozitie ![]() ,
, 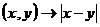 . Sa se alcatuiasca tabla legii .
. Sa se alcatuiasca tabla legii .
|
1 2 3 4 |
|
Definitie. Fie M
o multime pe care este data o lege de compozitie ![]() . O submultime
. O submultime ![]() a lui
a lui ![]() cu proprietatea :
cu proprietatea :
![]()
se numeste parte stabila a lui ![]() in raport cu legea de
compozitie
in raport cu legea de
compozitie ![]() .
.
Observatie.
Daca ![]() este parte
stabila a lui
este parte
stabila a lui ![]() in raport cu legea de
compozitie
in raport cu legea de
compozitie ![]() , atunci pe
, atunci pe ![]() putem defini legea de
compozitie
putem defini legea de
compozitie ![]() , punand
, punand
![]()
Vom spune ca ![]() este legea de compozitie indusa pe
este legea de compozitie indusa pe ![]() de catre
de catre ![]() .
.
Exemplu
Pentru ce valori ale parametrului real ![]() , intervalul
, intervalul ![]() este o parte
stabila a lui
este o parte
stabila a lui ![]() in raport cu legea de
compozitie :
in raport cu legea de
compozitie :
![]() .
.
![]() este o parte
stabila a lui
este o parte
stabila a lui ![]() in raport cu legea de
compozitie
in raport cu legea de
compozitie ![]() , daca :
, daca :
![]()
![]() .
.
Cum ![]() .
.
Proprietati ale legilor de compozitie
Definitie. O
lege de compozitie ![]() ,
, ![]() , se numeste asociativa,
daca :
, se numeste asociativa,
daca :
![]() .
.
Definitie. O
lege de compozitie ![]() ,
, ![]() , se numeste comutativa,
daca :
, se numeste comutativa,
daca :
![]() .
.
Definitie. Un
element ![]() se numeste element neutru pentru o lege de
compozitie
se numeste element neutru pentru o lege de
compozitie ![]() ,
, ![]() , daca :
, daca :
![]() .
.
Teorema. Daca o lege de compozitie are element neutru, atunci acesta este unic.
Demonstratie. Fie ![]() si
si ![]() doua elemente
neutre pentru o lege de compozitie
doua elemente
neutre pentru o lege de compozitie ![]() ,
, ![]() . Avem
. Avem ![]() deoarece
deoarece ![]() este element neutru.
De asemenea,
este element neutru.
De asemenea, ![]() caci si
caci si ![]() este element neutru,
de unde
este element neutru,
de unde ![]() .
.
Definitie. Un
element ![]() se numeste simetrizabil in raport cu legea
de compozitie (asociativa si cu element neutru, fie acesta
se numeste simetrizabil in raport cu legea
de compozitie (asociativa si cu element neutru, fie acesta ![]() )
) ![]() ,
, ![]() , daca exista
, daca exista ![]() astfel incat :
astfel incat :
![]() .
.
Observatie.
Daca ![]() satisface ca si
satisface ca si ![]() conditiile
conditiile ![]() , atunci
, atunci ![]() . Intr-adevar,
. Intr-adevar, ![]() . Daca
. Daca ![]() este simetrizabil,
atunci unicul element
este simetrizabil,
atunci unicul element ![]() cu proporietatea
cu proporietatea ![]() se numeste simetricul lui
se numeste simetricul lui ![]() (in raport cu
operatia
(in raport cu
operatia ![]() ).
).
Teorema.
Daca ![]() sunt elemente
simetrizabile in raport cu o lege de compozitie
sunt elemente
simetrizabile in raport cu o lege de compozitie ![]() ,
, ![]() (asociativa
si cu element neutru) atunci
(asociativa
si cu element neutru) atunci ![]() si
si ![]() sunt simetrizabile.
Mai mult :
sunt simetrizabile.
Mai mult :
Demonstratie. 1. Avem ![]()
![]() .
.
Analog, ![]() .
.
2. Rezulta imediat din relatia ![]() .
.
Exemple
1. Pe ![]() definim legea de
compozitie
definim legea de
compozitie ![]() ,
, ![]() . Aratati ca aceasta lege de
compozitie este asociativa, comutativa si cu element
neutru. Intervalul
. Aratati ca aceasta lege de
compozitie este asociativa, comutativa si cu element
neutru. Intervalul ![]() este o parte
stabila a lui
este o parte
stabila a lui ![]() in raport cu legea de
compozitie
in raport cu legea de
compozitie ![]() .
.
Studiem asociativitatea :
![]()
Scriem separat fiecare membru si il dezvoltam :
![]()
![]()
Din ![]() si
si ![]() rezulta ca
rezulta ca ![]() si deci legea
este asociativa.
si deci legea
este asociativa.
Studiem comutativitatea :
![]()
![]() , deci legea este comutativa.
, deci legea este comutativa.
Studiem existenta elementului neutru :
![]() astfel incat
astfel incat ![]()
Intrucat legea de compozitie este
comutativa, este suficient sa pornim cu una din egalitatile
: ![]() sau
sau ![]() , deoarece
, deoarece ![]() . Sa pornim spre exemplu cu prima egalitate :
. Sa pornim spre exemplu cu prima egalitate :
![]() si cum egalitatea
este verificata pentru orice
si cum egalitatea
este verificata pentru orice ![]() , rezulta ca
, rezulta ca ![]() , deci elementul neutru al legii este
, deci elementul neutru al legii este ![]() .
.
Aratam ca ![]() este o parte
stabila a lui
este o parte
stabila a lui ![]() in raport cu legea de
compozitie
in raport cu legea de
compozitie ![]() :
:
![]() .
.
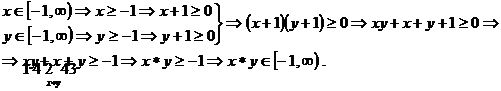
Deci ![]() este o parte
stabila a lui
este o parte
stabila a lui ![]() in raport cu legea de
compozitie
in raport cu legea de
compozitie ![]() .
.
2. In multimea ![]() se defineste
legea de compozitie, notata prin
se defineste
legea de compozitie, notata prin ![]() ,
, ![]() . Sa se arate
ca aceasta lege este comutativa, asociativa, admite un
element neutru si orice element admite un simetric,
. Sa se arate
ca aceasta lege este comutativa, asociativa, admite un
element neutru si orice element admite un simetric, ![]() .
.
Studiem asociativitatea :
![]()
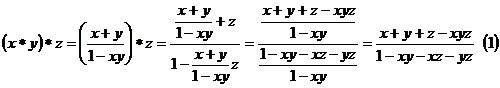
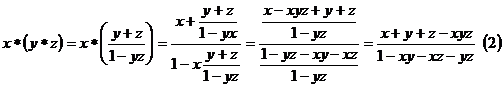
Din ![]() si
si ![]() rezulta ca
rezulta ca ![]() si deci legea
este asociativa.
si deci legea
este asociativa.
Studiem comutativitatea :
![]()
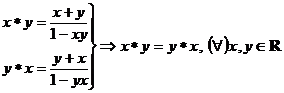 si deci legea
este comutativa .
si deci legea
este comutativa .
Studiem existenta elementului neutru :
![]() astfel incat
astfel incat ![]()
Deoarece legea este comutativa, este
suficient sa pornim cu una din egalitati. Pornim cu cea de a
doua : ![]() .
.
Deci elementul neutru este ![]() .
.
Studiem existenta elementelor inversabile :
![]() astfel incat
astfel incat ![]() .
.
Pornim de la ![]() , deci inversul (simetricul) unui element
, deci inversul (simetricul) unui element ![]() este
este
![]() .
.
Structuri algebrice
Definitie. O
multime nevida ![]() se numeste monoid in raport cu o lege de
compozitie definita pe
se numeste monoid in raport cu o lege de
compozitie definita pe ![]() ,
, ![]() ,
, ![]() , daca sunt satisfacute urmatoarele axiome :
, daca sunt satisfacute urmatoarele axiome :
![]()
![]() ;
;
![]()
![]() astfel incat
astfel incat ![]() ,
, ![]() .
.
Observatie. Cu alte cuvinte, pentru a arata ca o multime este monoid in raport cu o lege de compozitie, trebuie sa aratam partea stbila, asociativitatea si existenta elementului neutru.
Definitie.
Spunem ca monoidul ![]() este comutativ (sau abelian) daca operatia
acestuia satisface si axioma :
este comutativ (sau abelian) daca operatia
acestuia satisface si axioma :
![]() .
.
Exemplu
Fie ![]() .
.
1. Aratati ca ![]() este o parte
stabila a lui
este o parte
stabila a lui ![]() in raport cu
inmultirea si ca formeza monoid comutativ in raport cu
operatia indusa.
in raport cu
inmultirea si ca formeza monoid comutativ in raport cu
operatia indusa.
2. Determinati elementele simetrizabile
ale monoidului ![]() .
.
1. Aratam ca ![]() este o parte
stabila a lui
este o parte
stabila a lui ![]() in raport cu
inmultirea :
in raport cu
inmultirea :
Fie ![]() , deci
, deci ![]() , unde
, unde ![]() si
si ![]() , unde
, unde ![]() . Trebuie sa aratam ca
. Trebuie sa aratam ca ![]() .
. ![]() , deci este de forma
, deci este de forma ![]() , unde
, unde ![]() si deci
si deci ![]() , adica
, adica ![]() este o parte
stabila a lui
este o parte
stabila a lui ![]() in raport cu
inmultirea .
in raport cu
inmultirea .
Trebuie sa aratam ca ![]() formeza monoid
comutativ in raport cu inmultirea, adica inmultirea pe
formeza monoid
comutativ in raport cu inmultirea, adica inmultirea pe ![]() este asociativa,
comutativa si admite element neutru .
este asociativa,
comutativa si admite element neutru .
Inmultirea pe ![]() este evident
asociativa si comutativa, deoarece pe multimea
este evident
asociativa si comutativa, deoarece pe multimea ![]() a numerelor complexe,
inmultirea este asociativa si comutativa, iar
a numerelor complexe,
inmultirea este asociativa si comutativa, iar ![]() este submultime a
lui
este submultime a
lui ![]() . De asemenea, elementul neutru este elementul neutru de la
inmultirea numerelor complexe, adica
. De asemenea, elementul neutru este elementul neutru de la
inmultirea numerelor complexe, adica ![]() .
.
2. Determinam elementele simetrizabile :
![]() este simetrizabil
daca
este simetrizabil
daca ![]() astfel incat
astfel incat 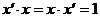 .
.
Fie ![]() si
si ![]() astfel incat
astfel incat ![]()
![]() (deoarece avem
egalitate de numere complexe, adica partea reala egala cu partea
reala si partea imaginara egala cu partea imaginara).
(deoarece avem
egalitate de numere complexe, adica partea reala egala cu partea
reala si partea imaginara egala cu partea imaginara).
Consideram ultimul sistem ca un sistem cu
necunoscutele ![]() ,
,![]() si cu parametrii
si cu parametrii ![]() .
.
Determinantul sistemului este ![]() .
.
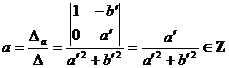 ,
, 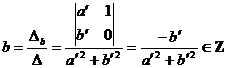 , dar
, dar ![]() sunt numere intregi,
deci
sunt numere intregi,
deci ![]() sau
sau ![]() sau
sau 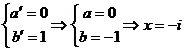 sau
sau
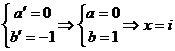 . Deci singurele elemente simetrizabile ale lui
. Deci singurele elemente simetrizabile ale lui ![]() in raport cu
inmultirea sunt :
in raport cu
inmultirea sunt : ![]() si
si ![]() .
.
Observatie.
Dupa cum am vazut mai sus, asociativitatea, comutativitatea si
existenta elementului neutru nu au mai trebuit demonstrate, deoarece ![]() este submultime a
lui
este submultime a
lui ![]() , la fel se intampla si in cazul matricilor,
inmultirea este asociativa si admite ca element neutru pe
, la fel se intampla si in cazul matricilor,
inmultirea este asociativa si admite ca element neutru pe ![]() .
.
Definitie. Un
cuplu ![]() format cu o
multime nevida
format cu o
multime nevida ![]() si cu o lege de
compzitie pe
si cu o lege de
compzitie pe ![]() ,
, ![]() se numeste grup daca sunt
satisfacute urmatoarele axiome :
se numeste grup daca sunt
satisfacute urmatoarele axiome :
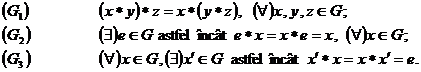
Observatie. Un
monoid ![]() cu proprietatea
ca orice element
cu proprietatea
ca orice element ![]() este simetrizabil (in
raport cu operatia acestuia) se numeste grup.
este simetrizabil (in
raport cu operatia acestuia) se numeste grup.
Definitie.
Spunem ca cuplul ![]() este grup abelian sau grup comutativ, daca
satisface si axioma :
este grup abelian sau grup comutativ, daca
satisface si axioma :
![]() .
.
Exemplu
Fie ![]() . Aratati ca corespondenta
. Aratati ca corespondenta ![]() este o lege de
compozitie pe
este o lege de
compozitie pe ![]() si ca
si ca ![]() este grup comutativ.
este grup comutativ.
Aratam ca ![]() este lege interna
pe
este lege interna
pe ![]() . Cu alte cuvinte, trebuie sa aratam ca
. Cu alte cuvinte, trebuie sa aratam ca ![]() este parte
stabila a lui
este parte
stabila a lui ![]() in raport cu
in raport cu ![]() .
.
Fie ![]() , deoarece un numar pozitiv la orice putere ne da
un numar pozitiv. Presupunem ca
, deoarece un numar pozitiv la orice putere ne da
un numar pozitiv. Presupunem ca ![]()
![]() sau
sau ![]() si cum
si cum ![]()
![]()
![]() este parte
stabila a lui
este parte
stabila a lui ![]() in raport cu
in raport cu ![]() .
.
Studiem asociativitatea :
![]()
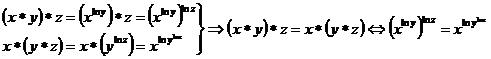 . Daca logaritmam ultima relatie, obtinem
:
. Daca logaritmam ultima relatie, obtinem
: ![]() afirmatie
adevarata
afirmatie
adevarata ![]() , deci legea este asociativa.
, deci legea este asociativa. ![]()
Studiem comutativitatea :
![]()
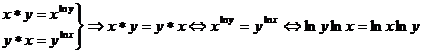 (prin logaritmare),
afirmatie adevarata
(prin logaritmare),
afirmatie adevarata ![]() , deci legea de compozitie este comutativa.
, deci legea de compozitie este comutativa. ![]()
Studiem existenta elementului neutru :
![]() astfel incat
astfel incat ![]() sau pentru a nu se
produce confuzie cu baza logaritmului natural, daca notam elementul
neutru cu
sau pentru a nu se
produce confuzie cu baza logaritmului natural, daca notam elementul
neutru cu ![]() , avem :
, avem :
![]() astfel incat
astfel incat ![]() .
.
Pornim de la ![]() , deci elementul neutru este chiar baza logaritmilor
naturali.
, deci elementul neutru este chiar baza logaritmilor
naturali. ![]()
Aratam ca toate elementele sun simetrizabile :
![]()
Pornim de la ![]() , deci orice element
, deci orice element ![]() este simetrizabil
si simetricul sau este
este simetrizabil
si simetricul sau este ![]() .
. ![]()
Din ![]() ,
, ![]() ,
, ![]() si
si ![]() rezulta ca
rezulta ca ![]() este grup comutativ.
este grup comutativ.
Observatie. In
orice linie (coloana) a tablei operatiei unui grup ![]() , cu un numar finit de elemente, fiecare element al lui
, cu un numar finit de elemente, fiecare element al lui ![]() apare o data
si numai o data.
apare o data
si numai o data.
Teorema. Intr-un
grup ![]() sunt adevarate
regulile de simplificare la stanga si la dreapta :
sunt adevarate
regulile de simplificare la stanga si la dreapta :
![]()
si respectiv
![]() .
.
Demonstratie. Presupunem ca pentru ![]() avem
avem ![]() si fie
si fie ![]() simetricul lui
simetricul lui ![]() . Avem :
. Avem : ![]() , deci
, deci ![]() , de unde rezulta ca este adevarata
regula de simplificare la stanga. Analog se demonstreaza regula de
simplificare la dreapta.
, de unde rezulta ca este adevarata
regula de simplificare la stanga. Analog se demonstreaza regula de
simplificare la dreapta.
Teorema. Fie ![]() un grup. Oricare ar fi
un grup. Oricare ar fi
![]() , ecuatiile :
, ecuatiile :
![]() si
si ![]()
au solutii unice in ![]() , anume
, anume ![]() , respectiv
, respectiv ![]() , unde
, unde ![]() este simetricul lui
este simetricul lui ![]() .
.
Demonstratie. Daca ![]() si
si ![]() sunt solutii din
sunt solutii din ![]() ale ecuatiei
ale ecuatiei ![]() , atunci
, atunci ![]() , deci
, deci ![]() si folosind
regula de simplificare la stanga obtinem
si folosind
regula de simplificare la stanga obtinem ![]() . Asadar, ecuatia
. Asadar, ecuatia ![]() are cel mult o
solutie in
are cel mult o
solutie in ![]() .
.
Fie ![]() , unde
, unde ![]() este simetricul lui
este simetricul lui ![]() . Avem :
. Avem : ![]() , de unde rezulta ca
, de unde rezulta ca ![]() este solutie (din
este solutie (din
![]() ) a ecuatiei
) a ecuatiei ![]() , unica conform primei parti a
demonstratiei. Analog se arata ca
, unica conform primei parti a
demonstratiei. Analog se arata ca ![]() admite solutia
unica,
admite solutia
unica, ![]() .
.
Exemplu
Fie ![]() un grup cu
un grup cu ![]() elemente si
elemente si ![]() elementul neutru al
lui
elementul neutru al
lui ![]() . Demonstrati in cazul in care
. Demonstrati in cazul in care ![]() este comutativ ca
este comutativ ca
![]() ,
, ![]() .
.
Fie ![]() elementele grupului
elementele grupului ![]() si fie
si fie ![]() un element arbitrar
din
un element arbitrar
din ![]() . Conform Observatiei de mai sus, elementele
. Conform Observatiei de mai sus, elementele ![]() coincid mai putin
ordinea cu
coincid mai putin
ordinea cu ![]() si cum
si cum ![]() este comutativ avem :
este comutativ avem :
![]()
asadar ![]() si prin
simplificare la dreapta se obtine
si prin
simplificare la dreapta se obtine ![]() .
.
Definitie. Fie ![]() un grup. O
submultime nevida
un grup. O
submultime nevida ![]() a lui
a lui ![]() se numeste subgrup al lui
se numeste subgrup al lui ![]() daca sunt
satisfacute urmatoarele conditii :
daca sunt
satisfacute urmatoarele conditii :
unde ![]() este simetricul lui
este simetricul lui ![]() (in raport cu operatia lui
(in raport cu operatia lui ![]() ).
).
Teorema. Fie ![]() un grup,
un grup, ![]() elementul neutru al
lui
elementul neutru al
lui ![]() si
si ![]() un subgrup al lui
un subgrup al lui ![]() . Atunci :
. Atunci :
![]() ,
,
![]() este grup in raport cu
operatia indusa pe
este grup in raport cu
operatia indusa pe ![]() de catre
operatia grupului
de catre
operatia grupului ![]() .
.
Demonstratie. 1. Cum ![]() putem alege un element
putem alege un element
![]() . Din 2. rezulta ca si
. Din 2. rezulta ca si ![]() si acum din 1.
rezulta ca
si acum din 1.
rezulta ca ![]() .
.
2. Sa notam cu ![]() operatia grupului
operatia grupului
![]() ,
, ![]() . Din 1. rezulta ca
. Din 1. rezulta ca ![]() este o parte
stabila a lui
este o parte
stabila a lui ![]() in raport cu cu
operatia
in raport cu cu
operatia ![]() . Fie
. Fie ![]() legea de
compozitie indusa pe
legea de
compozitie indusa pe ![]() de
de ![]() ,
,
![]() .
.
Evident ![]() este asociativa
(caci
este asociativa
(caci ![]() este asociativa)
si admite ca element neutru pe
este asociativa)
si admite ca element neutru pe ![]() . Daca
. Daca ![]() , atunci simetricul sau
, atunci simetricul sau ![]() in raport cu
in raport cu ![]() se gaseste
in
se gaseste
in ![]() , deci este simetric al lui
, deci este simetric al lui ![]() in raport cu
in raport cu ![]() . Rezulta ca
. Rezulta ca ![]() este grup.
este grup.
Exemple
1. Fie ![]() un grup,
un grup, ![]() elementul sau neutru
si
elementul sau neutru
si ![]() . Atunci
. Atunci ![]() este subgrup al lui
este subgrup al lui ![]() , numit subgrupul unitate. Intr-adevar, daca
, numit subgrupul unitate. Intr-adevar, daca ![]() , atunci
, atunci ![]() , deci
, deci
![]() ,
, ![]() .
.
2. Fie ![]() un numar intreg
si
un numar intreg
si ![]() multimea tuturor
multiplilor numarului
multimea tuturor
multiplilor numarului ![]() ,
,
![]()
Atunci ![]() este subgrup al
grupului
este subgrup al
grupului ![]() . Intr-adevar, daca
. Intr-adevar, daca ![]() , exista
, exista ![]() astfel incat
astfel incat ![]() ,
, ![]() . Rezulta ca
. Rezulta ca ![]() ,
, ![]() , deci
, deci ![]() este subgrup al lui
este subgrup al lui ![]() .
.
Definitie. Fie ![]() un grup,
un grup, ![]() si
si ![]() . Spunem ca
. Spunem ca ![]() este element de ordin
este element de ordin ![]() al grupului
al grupului ![]() daca
daca ![]() si
si ![]() ,
, ![]() .
.
Definitie. Fie ![]() si
si ![]() doua grupuri. O
aplicatie
doua grupuri. O
aplicatie ![]() se numeste morfism de grupuri daca :
se numeste morfism de grupuri daca :
![]() .
.
Teorema. Fie ![]() si
si ![]() doua grupuri,
doua grupuri, ![]() si
si ![]() elementele neutre ale
lui
elementele neutre ale
lui ![]() si
si ![]() respectiv. Daca
respectiv. Daca ![]() este un morfism de
grupuri, atunci :
este un morfism de
grupuri, atunci :
unde ![]() este simetricul lui
este simetricul lui ![]() , iar
, iar ![]() este simetricul lui
este simetricul lui ![]() .
.
Demonstratie. 1. Avem :
![]()
si prin simplificare cu ![]() se obtine
se obtine ![]() .
.
2. Pentru orice ![]() , avem :
, avem :
![]() , deci
, deci ![]() si analog
si analog ![]() , de unde
, de unde ![]() .
.
Definitie. Fie ![]() si
si ![]() doua grupuri. O
aplicatie bijectiva
doua grupuri. O
aplicatie bijectiva ![]() se numeste izomorfism de grupuri daca :
se numeste izomorfism de grupuri daca :
![]() .
.
Teorema. Fie ![]() si
si ![]() doua grupuri.
Daca
doua grupuri.
Daca ![]() este izomorfism.
Atunci si
este izomorfism.
Atunci si ![]() este izomorfism.
este izomorfism.
Demonstratie.Fie ![]() . Cum
. Cum ![]() este aplicatie
bijectiva exista
este aplicatie
bijectiva exista ![]() unic determinati
astfel incat
unic determinati
astfel incat ![]() si
si ![]() . Conform definitiei aplicatiei
. Conform definitiei aplicatiei ![]() avem
avem ![]() si
si ![]() . Dar
. Dar ![]() , de unde
, de unde ![]() si cum
si cum ![]() este aplicatie
bijectiva, rezulta ca
este aplicatie
bijectiva, rezulta ca ![]() este izomorfism.
este izomorfism.
Definitie. Fie ![]() un grup. Un izomorfism (morfism)
un grup. Un izomorfism (morfism) ![]() se numeste automorfism (resp. endomorfism) al grupului
se numeste automorfism (resp. endomorfism) al grupului ![]() .
.
Exemplu
Pe multimea ![]() se defineste
legea de compozitie interna
se defineste
legea de compozitie interna ![]() .
.
1. Sa se arate ca ![]() este grup abelian .
este grup abelian .
2. Considerand si grupul ![]() sa se arate
ca
sa se arate
ca ![]() .
.
Prima parte a fost demonstrata mai sus. Pentru
a arata ca cele doua grupuri sun izomorfe, trebuie sa
determinam un morfism bijectiv intre cele doua grupuri. Trebuie, deci
sa determinam o functie ![]() bijectiva, astfel
incat
bijectiva, astfel
incat ![]() sau altfel spus
sau altfel spus ![]() . Cea mai naturala alegere ar fi
. Cea mai naturala alegere ar fi ![]() , functie care verifica morfismul :
, functie care verifica morfismul : ![]() si este evident
inversabila, inversa ei fiind
si este evident
inversabila, inversa ei fiind ![]() si deci este
bijectiva. (O functie este inversabila daca si numai
daca este bijectiva).
si deci este
bijectiva. (O functie este inversabila daca si numai
daca este bijectiva).
Definitie. O
multime nevida ![]() , luata impreuna cu doua legi de
compozitie
, luata impreuna cu doua legi de
compozitie
![]()
si
![]()
se numeste inel daca :
![]() este grup abelian,
este grup abelian,
![]() este monoid,
este monoid,
![]() Distributivitatea :
Distributivitatea : ![]()
![]() .
.
Definitie. Daca a doua operatie a inelului satisface si axioma :
![]()
spunem ca A este inel comutativ.
Exemplu
Inelul matricilor patratice.
Fie ![]() un inel. Inelul
un inel. Inelul ![]() poate fi oricare din
inelele
poate fi oricare din
inelele ![]() , etc. Notam cu
, etc. Notam cu ![]() multimea tuturor
matricelor
multimea tuturor
matricelor ![]() patratice de
ordin 2 cu coeficienti din
patratice de
ordin 2 cu coeficienti din ![]() ,
, 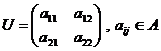 .
.
Daca
![]() ,
, 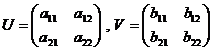 , definim matricile
, definim matricile ![]() si
si ![]() prin
prin 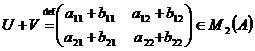
si
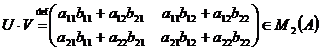 .
.
Matricele ![]() si
si ![]() ,
,
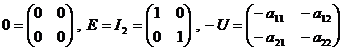
se numesc respectiv matricea zero, matricea
unitate, opusa matricei ![]() .
.
Reamintim o serie de proprietati ale
adunarii si inmultirii matricelor din ![]() . Demonstratiile multora dintre ele se fac invocand
proprietati ale adunarii si anmultirii numerelor
reale, care sunt de asemenea adevarate pentru adunarea si
inmultirea oricarui inel
. Demonstratiile multora dintre ele se fac invocand
proprietati ale adunarii si anmultirii numerelor
reale, care sunt de asemenea adevarate pentru adunarea si
inmultirea oricarui inel ![]() . Din acest motiv, asemenea demonstratii pot fi
reproduse si pentru matricele din
. Din acest motiv, asemenea demonstratii pot fi
reproduse si pentru matricele din ![]() . Pe aceasta cale se pot demonstra :
. Pe aceasta cale se pot demonstra :
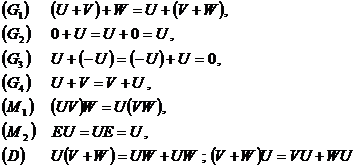
oricare ar fi ![]() .
.
Rezulta ca adunarea si anmultirea
matricelor confera lui ![]() o structura de
inel. La fel se organizeaza ca inel multimea
o structura de
inel. La fel se organizeaza ca inel multimea ![]() a matricelor
patratice de ordin
a matricelor
patratice de ordin ![]() cu coeficienti
din
cu coeficienti
din ![]() .
.
Definitie. Fie ![]() un inel,
un inel, ![]() elementul neutru in
raport cu prima operatie. Spunem ca a este inel fara divizori ai lui zero daca
elementul neutru in
raport cu prima operatie. Spunem ca a este inel fara divizori ai lui zero daca ![]() si
si ![]() . Un inel comutativ, cu cel putin doua elemente
si fara divizori ai lui zero se numeste domeniu de integritate.
. Un inel comutativ, cu cel putin doua elemente
si fara divizori ai lui zero se numeste domeniu de integritate.
Definitie. Fie ![]() si
si ![]() doua inele
si
doua inele
si ![]() . Aplicatia
. Aplicatia ![]() se numeste izomorfism de inele, daca :
se numeste izomorfism de inele, daca :
i. ![]() este functie
bijectiva
este functie
bijectiva
ii. ![]() este morfism de inele,
adica :
este morfism de inele,
adica :
1. ![]()
2. ![]() , pentru
, pentru ![]() .
.
Exemplu :
Aplicatia ![]() ,
, ![]() este un morfism
injectiv de inele. Intr-adevar, pentru orice
este un morfism
injectiv de inele. Intr-adevar, pentru orice ![]() avem :
avem :
![]()
![]()
![]() .
.
Injectivitatea lui ![]() este evidenta .
este evidenta .
Definitie. Un
inel ![]() se numeste corp daca elementele neutre
ale celor doua legi sunt diferite si orice element
se numeste corp daca elementele neutre
ale celor doua legi sunt diferite si orice element ![]() , diferit de elementul neutru al primei legi este
simetrizabil in raport cu cea de a doua lege. Un corp se numeste comutativ
daca a doua lege este comutativa.
, diferit de elementul neutru al primei legi este
simetrizabil in raport cu cea de a doua lege. Un corp se numeste comutativ
daca a doua lege este comutativa.
Exemple
1. Corpurile
de numere patratice ![]() . Fie
. Fie ![]() un intreg liber de
patrate (care nu se divide cu patratul niciunui numar intreg) si
un intreg liber de
patrate (care nu se divide cu patratul niciunui numar intreg) si
![]()
Daca ![]() ,
, ![]() ,
, ![]() , cu
, cu ![]() , atunci
, atunci
![]() ,
,
![]()
deci ![]() este o parte
stabila a lui
este o parte
stabila a lui ![]() in raport cu adunarea
si inmultirea. Observand ca
in raport cu adunarea
si inmultirea. Observand ca ![]() ,
, ![]() se deduce usor
ca
se deduce usor
ca ![]() este inel comutativ in
raport cu operatiile induse pe
este inel comutativ in
raport cu operatiile induse pe ![]() de adunarea si
inmultirea lui
de adunarea si
inmultirea lui ![]() . Pentru a dovedi ca
. Pentru a dovedi ca ![]() este corp mai
ramane sa aratam ca pentru orice
este corp mai
ramane sa aratam ca pentru orice ![]() ,
, ![]() ,
, ![]() , exista
, exista ![]() astfel incat
astfel incat ![]() .
.
Daca
![]() , atunci
, atunci ![]() sau
sau ![]() . Rezulta ca
. Rezulta ca ![]() (daca
(daca ![]() si
si ![]() deducem si
deducem si ![]() , iar daca
, iar daca ![]() si
si ![]() deducem
deducem ![]() , ambele situatii fiind contradictorii.
, ambele situatii fiind contradictorii.
Fie
![]() si avem :
si avem : ![]() .
.
Rezulta ca ![]() formeaza corp
fata de operatiile induse de adunarea si inmultirea
din
formeaza corp
fata de operatiile induse de adunarea si inmultirea
din ![]() , numit corp de numere
patratice. Astfel
, numit corp de numere
patratice. Astfel ![]() ,
, ![]() ,
, ![]() , etc. sunt corpuri de numere patratice.
, etc. sunt corpuri de numere patratice.
2. Inelul ![]() nu este corp, deoarece
nu este corp, deoarece
![]() , oricare ar fi
, oricare ar fi ![]() , deci 2 nu este inversabil in raport cu inmultirea lui
, deci 2 nu este inversabil in raport cu inmultirea lui ![]() .
.
Observatie. Morfismele si izomorfismele de corpuri se definesc in acelasi mod ca la inele (corpurile sunt prin definitie in particular si inele) si se probeaza la fel ca la inele.
Inelul claselor de resturi modulo n
Fie ![]() un numar intreg.
Conform teoremei impartirii cu rest, pentru orice
un numar intreg.
Conform teoremei impartirii cu rest, pentru orice ![]() exista
exista ![]() unic determinati
astfel incat :
unic determinati
astfel incat :
![]() .
.
Numarul unic determinat ![]() din relatia
precedenta, numit restul impartirii lui
din relatia
precedenta, numit restul impartirii lui ![]() prin
prin ![]() , s-a notat cu
, s-a notat cu ![]() si s-a numit restul modulo
si s-a numit restul modulo ![]() al lui
al lui ![]() .
.
Exemple
Ca rezultat al impartirii numerelor
intregi prin ![]() sunt posibile
resturile :
sunt posibile
resturile :
![]() .
.
Prin impartirea lui ![]() la
la ![]() se obtine restul
se obtine restul ![]() daca si
numai daca
daca si
numai daca ![]() este de forma
este de forma ![]() , cu
, cu ![]() . Multimile de numere :
. Multimile de numere :
![]() ,
,
unde
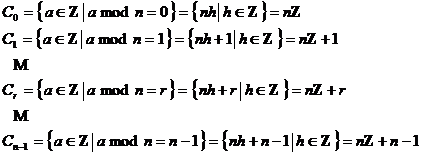
se numesc clase de resturi modulo n.
Asadar,
un numar intreg ![]() apartine clasei
apartine clasei ![]() daca si numai
daca
daca si numai
daca ![]() impartit la
impartit la ![]() da restul
da restul ![]() ,
,
![]() .
.
In
particular ![]() pentru
pentru ![]() . Clasa de resturi
. Clasa de resturi ![]() se noteaza de regula
cu
se noteaza de regula
cu ![]() . Asadar
. Asadar
![]() .
.
Sa
notam cu ![]() multimea claselor
de resturi modulo
multimea claselor
de resturi modulo ![]() ,
,
![]() .
.
Daca ![]() , definim suma
, definim suma ![]() si produsul
si produsul ![]() prin :
prin :
![]() ,
, ![]() .
.
Se
definesc astfel pe ![]() , doua legi de compozitie :
, doua legi de compozitie :
![]() ,
, ![]() si
si ![]() ,
, ![]() , numite adunarea,
respectiv inmultirea claselor de
resturi modulo n.
, numite adunarea,
respectiv inmultirea claselor de
resturi modulo n.
Exemplu
Pentru ![]() avem
avem ![]() si tablele
adunarii si inmultirii claselor de resturi modulo 6 sunt :
si tablele
adunarii si inmultirii claselor de resturi modulo 6 sunt :
|
|
|
|
|
|
|
|
|
|
|
|
Teorema. Adunare
si inmultirea claselor de resturi modulo ![]() confera
multimii
confera
multimii ![]() o strutctura de
inel comutativ, numit inelul claselor de resturi modulo
o strutctura de
inel comutativ, numit inelul claselor de resturi modulo ![]() .
.
Teorema. In
inelul ![]() , un element
, un element ![]() este inversabil
daca si numai daca
este inversabil
daca si numai daca ![]() este relativ prim cu
este relativ prim cu ![]() (adica cel mai mare divizor comun al numerelor
(adica cel mai mare divizor comun al numerelor ![]() si
si ![]() este 1).
este 1).
Teorema. Fie ![]() un numar prim.
Atunci inelul
un numar prim.
Atunci inelul ![]() este corp.
este corp.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 7551
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved