| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Serii de timp cu doua componente
Evolutia dotarii populatiei cu aparate radio la 1000 de locuitori in perioada 1980-1994 este prezentata in tabelul de mai jos:
Tabelul nr. 1
Anul | ||||||||
|
Nr. de aparate radio la 1000 locuitori |
Anul | |||||||
|
Nr. de aparate radio la 1000 locuitori |
Se cere:
a) Sa se justifice utilizarea unui model aditiv cu doua componente pentru descrierea evolutiei fenomenului analizat;
b) Sa se estimeze componentele modelului formulat la punctul precedent si sa se verifice semnificatia acestuia;
c) Sa se estimeze valorile fenomenului pentru urmatorii 2 ani.
Rezolvare
a) In cazul seriilor cronologice sau a seriilor de timp, specificarea modelului porneste de la reprezentarea grafica a datelor, respectiv construirea cronogramei.
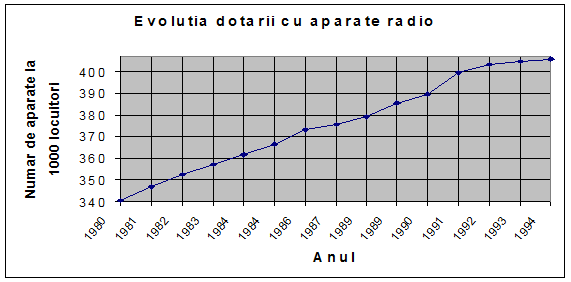
Deoarece, in perioada analizata, evolutia fenomenului prezinta o crestere permanenta, fara oscilatii semnificative, iar curba punctelor empirice prezinta o forma ce poate fi aproximata cu o dreapta, modelul ce poate fi utilizat pentru aproximarea fenomenului este de forma:
![]()
unde:
![]() =valorile inregistrate de fenomen in perioada analizata
(linia 2 din tabelul nr. 1);
=valorile inregistrate de fenomen in perioada analizata
(linia 2 din tabelul nr. 1);
![]() =componenta trend ce poate fi descrisa cu ajutorul unei
functii liniare:
=componenta trend ce poate fi descrisa cu ajutorul unei
functii liniare: ![]()
![]() =variabila reziduala.
=variabila reziduala.
b)
Modelul construit la punctul a) fiind ![]() , rezolvarea acestuia presupune estimarea celor doua
componente:
, rezolvarea acestuia presupune estimarea celor doua
componente:
![]() estimatia componentei trend;
estimatia componentei trend;
![]() estimatia variabilei reziduale.
estimatia variabilei reziduale.
Estimarea componentei trend se realizeaza cu ajutorul metodei celor mai mici patrate, care consta in minimizarea functiei:
![]()
Conditia de minim a acestei functii rezulta din:
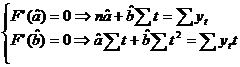
![]()
In urma efectuarii calculelor a rezultat urmatorul sistem de ecuatii:
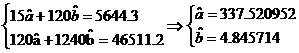
Pe baza estimatorilor se vor calcula valorile estimate ale componentei trend:
![]()
Valorile estimate ale variabilei reziduale vor rezulta din urmatoarea relatie:
![]()
In vederea testarii semnificatiei parametrilor si a modelului se vor calcula:
dispersia variatiei reziduale:
![]()
unde:
T =numarul de termeni ai seriei; T =15;
k =numarul variabilelor explicative; k =1;
![]()
abaterile medii patratice ale celor doi
estimatori ![]() si
si ![]() :
:
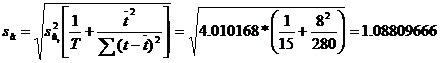
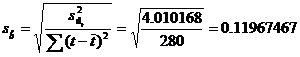
Deoarece numarul de
termeni al seriei este mai mic de 30, testarea estimatorilor se va face cu
ajutorul testului "t" - Student. Din tabela distributiei Student, pentru
un prag de semnificatie ![]() si in
functie de numarul gradelor de libertate v=n-k-1=13, se preia valoarea
si in
functie de numarul gradelor de libertate v=n-k-1=13, se preia valoarea ![]() .
.
![]()
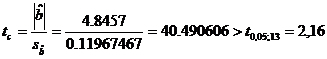
Deci, pentru un prag de semnificatie de 5%, ambii estimatori sunt semnificativ diferiti de zero.
valoarea raportului de corelatie:
![]()
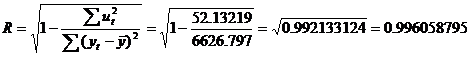
Testarea semnificatiei raportului de corelatie se realizeaza cu ajutorul testului Fisher-Snedecor:
![]()
Din tabela distributiei
Fisher-Snedecor, pentru un prag de semnificatie ![]() si in
functie de numarul gradelor de libertate
si in
functie de numarul gradelor de libertate ![]() =k=1 si
=k=1 si ![]() =T-k-1=13, se preia valoarea
=T-k-1=13, se preia valoarea ![]() .
.
Deoarece ![]() , valoarea raportului de corelatie este semnificativ
diferita de zero, pentru un prag de semnificatie
, valoarea raportului de corelatie este semnificativ
diferita de zero, pentru un prag de semnificatie ![]() .
.
In vederea verificarii independentei valorilor variabilei reziduale se va utiliza testul Durbin-Watson, care consta in calcularea valorii:
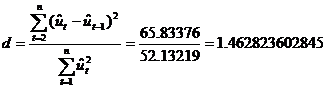
Din tabela distributiei
Durbin-Watson, pentru un prag de semnificatie ![]() , in functie de numarul observatiilor T=15 si de numarul
variabilelor exogene k=1, se preiau
valorile (pentru cazul n=15):
, in functie de numarul observatiilor T=15 si de numarul
variabilelor exogene k=1, se preiau
valorile (pentru cazul n=15): ![]() =1,08;
=1,08; ![]() =1,36.
=1,36.
Deoarece d=1,4628
> ![]() =1,36 si
=1,36 si
d=1,4628
< 4-![]() =2,64,
=2,64,
se poate accepta ipoteza de independenta a valorilor variabilei reziduale.
Verificarea verosimilitatii modelului se realizeaza cu ajutorul metodei analizei variatiei, calculele fiind prezentate in tabelul urmator:
|
Sursa de variatie |
Masura variatiei |
Nr. grade de libertate |
Dispersia corectata |
Valoarea testului F |
|
|
|
|
||||
|
Variatia explicata de tendinta |
|
k |
|
|
|
|
Variatia reziduala |
|
T-k- |
| ||
|
Variatia totala |
|
T- | |||
Deoarece ![]() , modelul este acceptat, cu un prag de semnificatie de
, modelul este acceptat, cu un prag de semnificatie de ![]() .
.
Din ecuatia analizei variatiei:
![]()
rezulta ca modelul explica 99.212% din variatia totala a numarului de aparate de radio la 1000 de locuitori.
In final, modelul econometric devine:
![]() ; R =
; R =![]()
(1,08809666) (0,11967467) d =1,4628
![]()
c) Deoarece modelul a fost acceptat ca semnificativ, acesta poate fi folosit la estimarea prognozei fenomenului analizat. Astfel, nivelul previzional al fenomenului va fi:
in 1995:
![]() =337.520952 + 4.8457*16 = 415.0521
=337.520952 + 4.8457*16 = 415.0521
Abaterea standard a nivelului previzionat al fenomenului va fi egala cu:
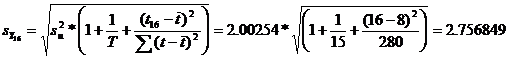
Intervalul
de incredere al prognozei fenomenului, estimat cu un prag de semnificatie ![]() , pentru care valoarea lui
, pentru care valoarea lui ![]() , preluata din tabela distributiei Student, este de
, preluata din tabela distributiei Student, este de
![]() , se calculeaza cu ajutorul relatiei:
, se calculeaza cu ajutorul relatiei:
![]()
![]()
![]()
in 1996:
![]() 337.520952 + 4.8457*17 = 419.8978
337.520952 + 4.8457*17 = 419.8978
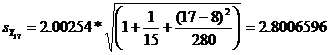
![]()
![]()
In concluzie, in urma efectuarii calculelor, se poate aprecia ca in 1995 nivelul fenomenului va fi cuprins in intervalul [409,0973; 421], iar in 1996 in intervalul [407.8935; 431.90201], probabilitatea de realizare a acestor prognoze fiind de 95%.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1940
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved