| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Serii Fourier
Definitie. O functie f:R→R se numeste periodica daca ![]() astfel incat
astfel incat ![]() ,
, ![]()
Exemple Functia constanta are ca perioada orice numar. Functiile sinx si cos x au perioadele 2 , …
Observatie. Avand in vedere ca orice
multiplu intreg de T (kT, k![]() ) este de asemenea perioada pentru f, cea mai mica perioada pozitiva T>0 se numeste perioada
principala a functiei f.
) este de asemenea perioada pentru f, cea mai mica perioada pozitiva T>0 se numeste perioada
principala a functiei f.
Propozitie. Daca ![]() este
periodica de perioada T,
atunci
este
periodica de perioada T,
atunci ![]() este
periodica de perioada T/
este
periodica de perioada T/
Demonstratie.
![]()
Exemplu. Functiile
sin x si cos x sunt periodice, de perioada 2 , functiile sin nx si cos nx au perioada 2 /n, iar perioada comuna a
functiilor ![]() este 2
este 2
Propozitie. Fie f:R→R periodica de perioada T,
integrabila pe R, atunci ![]() avem:
avem:
![]()
Definitie. Se numeste serie trigonometrica, o serie de forma:
![]()
unde ![]() sunt numere reale.
sunt numere reale.
Propozitie. Daca f:R→R este o functie integrabila pe R, periodica de perioada 2π, care poate fi reprezentata printr-o serie trigonometrica
![]()
atunci coeficientii ![]() se calculeaza
cu formulele :
se calculeaza
cu formulele :
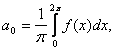
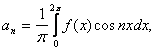
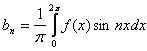
Definitie. Seria
trigonometrica a functiei ![]() ai carei
coeficienti se calculeaza cu ajutorul formulelor de mai sus se
numeste serie Fourier.
ai carei
coeficienti se calculeaza cu ajutorul formulelor de mai sus se
numeste serie Fourier.
Observatie. Tinand
seama de faptul ca integrala unei functii periodice de perioada
2 este
aceeasi pe orice interval de lungime 2 ,
coeficientii ![]() pot fi
calculati si astfel :
pot fi
calculati si astfel :
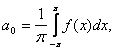
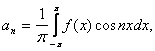
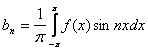
Integrala Fourier
Fie f : R → R o functie care nu este periodica. Functia f nu poate fi reprezentata printr-o serie Fourier pe axa reala.
Teorema. Daca functia f : R → R indeplineste urmatoarele conditii :
a) f ese monotona pe potiuni ;
b) f este marginita ;
c) f este continua, avand cel mult un numar finit de puncte de discontinuitate de prima speta ;
d) in oricare punct de discontinuitate, valoarea functiei se calculeaza astfel :
![]()
e) f este absolut integrabila pe R,
atunci functia ![]() poate fi reprezentata astfel :
poate fi reprezentata astfel :
![]()
care se numeste foma
complexa a integralei Fourier a functiei ![]()
Daca notam:
![]()
atunci
![]()
Definitie. Functia ![]() se numeste transformata
Fourier (directa) a functiei
se numeste transformata
Fourier (directa) a functiei ![]() , iar
, iar![]() se numeste inversa transformatei Fourier.
se numeste inversa transformatei Fourier.
Daca functia ![]() este para, se
obtine :
este para, se
obtine :
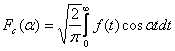
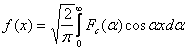
Definitie. Functia ![]() se numeste
transformata Fourier prin cosinus a functiei
se numeste
transformata Fourier prin cosinus a functiei ![]() , iar
, iar ![]() este inversa
transformatei Fourier prin cosinus.
este inversa
transformatei Fourier prin cosinus.
Daca functia ![]() este impara,
se obtine :
este impara,
se obtine :
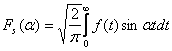
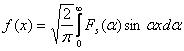
Definitie. Functia ![]() se numeste
transformata Fourier prin sinus a functiei
se numeste
transformata Fourier prin sinus a functiei ![]() , iar
, iar ![]() este inversa
transformatei Fourier prin sinus.
este inversa
transformatei Fourier prin sinus.
Exemple.
1. Sa se calculeze transformata Fourier a functiei
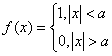
Transformata Fourier a functiei ![]() este
este
![]() ,
, ![]()
2. Sa se calculeze transformata Fourier a functiei
![]() R
R
Transformata Fourier a functiei ![]() este
este
![]()
3. Sa se calculeze transformatele Fourier prin cosinus si sinus
ale functiei ![]()
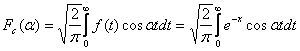
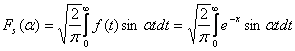
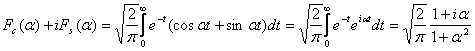
![]() ,
, ![]()
4. Sa se determine functia ![]() stiind ca
stiind ca
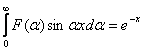 , unde
, unde ![]()
Ecuatia poate fi scrisa sub forma :
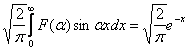
Aplicand inversa transformatei Fourier prin sinus, se obtine:
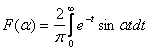
Proprietati ale transformatei Fourier
![]()
Demonstratie.
![]()
![]()
![]()
Propozitia 2. Transformarea Fourier directa are proprietatea de translatie.
![]()
![]() R
R
Demonstratie. ![]()
![]()
Se face substitutia ![]() si se obtine :
si se obtine :
![]()
Propozitia 3. Pentru orice ![]() , are
loc relatia :
, are
loc relatia :
![]()
Demonstratie.
Pentru a>0 facem substiutia ![]() si se
obtine:
si se
obtine:
![]()
Pentru a<0, avem :
![]()
Propozitia 4. Pentru orice numar real oarecare h, are loc relatia :
![]()
Demonstratie.
![]()
Propozitia 5 Pentru k intreg si pozitiv are loc relatia:
![]()
Demonstratie.
![]()
![]()
Presupunem, prin inductie, ca este adevarata pentru k-1
![]()
si demonstram pentru k
![]()
Definitie. Se numeste
produs de convolutie al functiilor ![]() si
si ![]() , integrala :
, integrala :
![]()
Propozitia
6. Tranfomarea Fourier a produsului de convoutie a functiilor ![]() si
si ![]() este data de
este data de
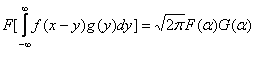
unde ![]() si
si ![]()
Demonstratie.
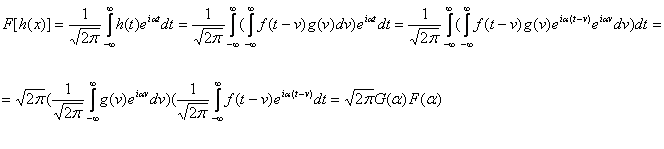
Tema de casa nr. 6
1. Sa se calculeze transformatele Fourier ale functiilor : 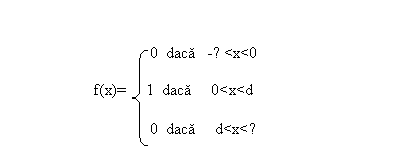
![]()
![]()
|
![]()
3. Sa se determine functia ![]() din ecuatia :
din ecuatia :
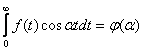
unde

|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 5109
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved