ANALIZA SI PREVIZIUNEA SERIILOR DE TIMP

Obiective

• Intelegerea si aplicarea metodelor de calcul a indicilor factoriali in analiza dinamicii indicatorilor economici;
• Cuantificarea dinamicii medii a unui indicator;
• Cunoasterea si utilizarea metodelor cantitative de previziune. Metoda clasica de descompunere a unei serii de timp.

Concepte de baza

Indice al variatiei integrale, indice factorial, indice al pretului;

Nivel mediu al unei serii de timp, indice mediu, ritm mediu, diferenta medie absoluta;

Serie de timp, model dinamic, functii de tendinta, coeficientii sezonalitatii, ciclicitate

Medii mobile, previziune, erori de previziune, netezire exponentiala.

Rezultate asteptate

Studentul intelege notiunile de indice factorial, nivel mediu, indice mediu, ritm mediu si stapaneste modalitatile de calcul a acestora. Utilizeaza metode cantitative in previziune; in acest sens, identifica componentele prezente intr-o serie de timp, modeleaza si extrapoleaza tendinta, utilizeaza adecvat o medie mobila, modeleaza componenta sezoniera si ciclica, utilizeaza metoda netezirii exponentiale in netezire si previziune.

Sinteza

1. INDICII STATISTICI

1.1. Indicii statistici: definitii si tipologii

Studiul fenomenelor economice si sociale presupune in marea majoritate a cazurilor si masurarea variatiei unor marimi. Aceasta variatie poate fi urmarita in timp, spatiu sau relativ la niste categorii. Se va folosi termenul generic de stare, notandu-se cu starea luata ca baza de comparatie si cu cea cercetata in raport cu aceasta. Se va nota cu marimea care constituie obiectul de studiu, variatia acesteia putand fi exprimata atat sub forma absoluta, cat si relativa.

Dintre exprimarile sub forma relativa un loc deosebit de important il ocupa indicele statistic. In practica variatia totala a variabilei Z este datorata variatiei unor alte variabile a caror evolutie intre doua stari si influenteaza evolutia lui Z. Avem de a face, asadar, cu Z de forma . Un astfel de model este un model de tip determinist in care cei factori determina in totalitate nivelul lui . In cazul unui astfel de model se pot distinge trei categorii de indici:

indicele variatiei totale (integrale) a marimii :

indici ai factorilor (individuali sau elementari):

indici ai variatiei partiale ale lui sau indici factoriali: - ne arata de cate ori s-a modificat in starea fata de starea sub influenta exclusiva a factorului .

1.2. Indicii factoriali

Indicii factoriali de tip Laspeyres. Acest indice este cel mai cunoscut si utilizat in practica economica. Mai poarta si denumirea de indicele preturilor. Daca se considera un cos de produse sau bunuri, volumul valoric al acestora se va calcula dupa relatia: . Indicele factorial al preturilor calculat prin metoda Laspeyres va avea expresia:

iar indicele factorial al cantitatilor (volumului fizic), expresia:

unde si sunt preturile din perioada de baza si perioada curenta, sunt cantitatile din perioada de baza, iar masoara importanta produsului sau bunului in cosul indicelui la momentul baza de comparatie.

Pentru cazul general, cand depinde de factori de influenta, iar forma functiei este oarecare, Florea (1986) deduce o regula pentru elaborarea indicilor factoriali de tip Laspeyres.

Indicii factoriali de tip Paasche. Acest indice a aparut tot ca un indice al preturilor, indicele factorial de pret de tip Paasche avand expresia:

iar cel factorial al cantitatilor (volumului fizic), expresia:

Pentru o functie oarecare , in care marimea depinde de factori, in Florea(1986) este prezentata o generalizare.

Indicii factoriali de tip Fisher. In 1922, I. Fisher propune o noua expresie de calcul a indicelui preturilor. Acesta se va obtine ca o medie geometrica a indicilor de pret de tip Laspeyres si Paasche, astfel:

De aceeasi maniera se obtine si indicele de volum:

Indicii factoriali generati prin Metoda Drumului Factorilor (MDF). Indicele factorial al unei variabile , in raport cu factorul , obtinut prin MDF este dat de relatia (Florea, 1989):

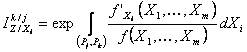
unde reprezinta portiunea arcului din drumul factorilor cuprins intre punctele si , acest drum fiind descris de ecuatiile parametrice , fiind in general un parametru legat de timp.

Exemple. Indicii factoriali calculati prin metoda Laspeyres.

O societate hoteliera dispune de 3 tipuri de locuri de cazare: camere cu un singur pat(single), camere cu doua paturi(double) si apartamente. Numarul de camere inchiriate (X) si tariful practicat (Y) in doua luni consecutive sunt date in tabelul urmator:

Volumul valoric al incasarilor din inchirierea camerelor (Z) se va calcula dupa relatia:

. Indicii factoriali de tip Laspeyres vor fi:

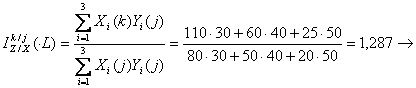volumul valoric al incasarilor a crescut in luna fata de luna de 1,287 ori sub influenta modificarii numarului de camere inchiriate. 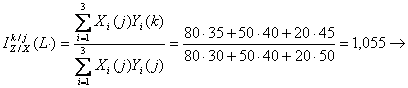volumul valoric al incasarilor a crescut in luna fata de luna de 1,055 ori sub influenta modificarii tarifului practicat.

Se considera marimea ca fiind profitul brut al unei societati si factorii - veniturile totale respectiv - cheltuielile totale ale aceleasi societati. Modelul care leaga cele trei marimi va fi de forma: . In doi ani consecutivi variabilele si au inregistrat valorile:

Expresiile si valorile indicilor factoriali de tip Laspeyres sunt:

- profitul brut a crescut in anul fata de anul de 2 ori sub influenta modificarii veniturilor totale;

- profitul brut a scazut in anul fata de anul de 0,5 ori sub influenta modificarii cheltuielilor totale.

1.3. Indicii factoriali de tip Laspeyres, Paasche si Fisher prin prisma abordarii axiomatice

Abordarea axiomatica se bazeaza pe stabilirea unor seturi de proprietati pe care un indice statistic trebuie sa le verifice (Buiga & all, 2003).

1. Principalii indici utilizati in economie

Indicele preturilor de consum este un indice de tip Laspeyres cu bazafixa:

unde: - reprezinta numarul de marfuri si servicii din cosul indicelui;

- reprezinta structura de consum, fiind ponderea marfii sau serviciului in consumul populatiei;

si sunt preturile inregistrate de marfa sau produsul in perioada de baza si perioada curenta;

Ponderile sunt obtinute prin Ancheta Integrata in Gospodarii si rezulta din structura cheltuielilor medii lunare efectuate de o gospodarie pentru cumpararea marfurilor si plata serviciilor necesare satisfacerii nevoilor de trai; aceste ponderi se actualizeaza la intervale de cativa ani. Preturile corespunzatoare celor marfuri si servicii din cosul indicelui se culeg lunar, in urma unei cercetari selective organizate de Institutul National de Statistica.

Indicele productiei industriale masoara evolutia de ansamblu a preturilor produselor si serviciilor industriale fabricate si livrate de producatorii interni in perioada curenta fata de perioada de baza, in primul stadiu de comercializare a produselor sau serviciilor. ndicele utlizat este tot un indice de tip Laspeyres.

Indicele salariilor masoara evolutia salariilor in perioada curenta fata de perioada de baza. Alaturi de indicele preturilor de consum este folosit in evaluarea nivelului de trai. Se utilizeaza, de asemenea, un indice de tip Laspeyres, care masoara variatia fondului de salarii total sub influenta modificarii salariilor medii corespunzatoare ramurii .

Indicii bursieri. Principalii indici bursieri se diferentiaza prin mai multe elemente: esantionarea, respectiv alegerea titlurilor din cosul indicelui, reprezentativitate, modul de calcul utilizat si natura variabilelor luate in calcul. Cei mai cunoscuti si urmariti indici bursieri, cu exceptia familiei de indici Dow Jones se calculeaza ca si indici Laspeyres.

2. PREVIZIUNEA SERIILOR DE TIMP

In derularea activitatii lor, frecvent agentii economici sunt pusi in situatia de a anticipa viitorul, iar apoi de a lua decizii in consecinta. Oamenii de afaceri sunt nevoiti sa previzioneze anual cifra de afaceri si alte elemente necesare intocmirii unui plan de afaceri, investitorii sunt interesati de profitul viitor degajat de investitie, respectiv guvernele de previziunea consumului sau a cheltuielilor guvernamentale etc.. Obtinerea rapida de previziuni utilizand modele cantitative de previziune este la indemana analistilor, urmare si a softurile de statistica accesibile si usor de exploatat.

Anticiparea, previziunea evolutiei viitoare a fenomenelor economice presupune in primul rand cunoasterea istoriei acestora, punerea in evidenta a unor legitati privind comportamentul lor trecut. Baza de date pe care se fundamenteaza analiza evolutiei fenomenelor in timp este constituita din serii cronologice.

2.1. Indicatori medii specifici seriilor cronologice

a) Nivelul mediu (valoarea medie). Nivelul mediu reprezinta nivelul teoretic atins de indicator in conditiile in care evolutia sa ar fi constanta in timp, factorii ce-i determina evolutia ar actiona cu aceeasi intensitate pe intreaga perioada de timp analizata.

Modul de determinare a volumului fenomenului difera dupa cum seria este de intervale respectiv de momente.

Pentru serii cronologice de intervale nivelul mediu este:

Pentru serii cronologice de momente nivelul mediu este definit de urmatoarea relatie:

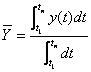
Daca se aproximeaza evolutia indicatorului ca fiind liniara intre doua momente consecutive de timp, rezulta:

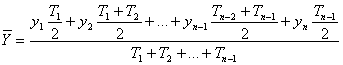
relatie numita medie cronologica ponderata.

Daca nivelul indicatorului se inregistreaza la momente echidistante (), atunci relatia anterioara devine:

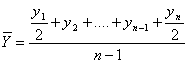
si reprezinta media cronologica simpla.

b) Indicele mediu. Ritmul mediu

Pentru calculul acestui indicator se intalnesc in literatura mai multe abordari.

Indicele mediu este parametrul modelului autoregresiv:

Utilizand metoda celor mai mici patrate pentru estimarea parametrului , se obtine urmatoarea expresie de calcul a indicelui mediu:

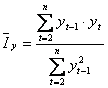
Metoda este intalnita in practica sub denumirea de metoda autoregresiva.

O alta expresie de calcul, adecvata pentru indicatori ce evolueaza aproximativ exponential este urmatoarea:

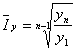
Ritmul mediu se determina pornind de la indicele mediu:

sau .

c) Diferenta medie absoluta

Expresia de calcul a diferentei medii absolute:

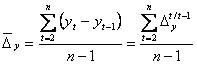
sau echivalent:

2.2. Componentele unei serii cronologice. Modelul clasic de descompunere

O serie cronologica este o secventa de observatii asupra unei variabile, ordonate dupa parametrul timp. Frecvent, masuratorile asupra variabilei sunt efectuate la intervale egale de timp, seria cronologica fiind prezentata sub forma:

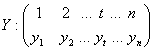
In abordarea traditionala, fluctuatiile din seriile cronologice sunt privite ca o rezultanta a suprapunerii urmatoarelor componente: tendinta T, componenta ciclica C, sezoniera S respectiv reziduala E. Primele trei componente sunt considerate deterministe, sistematice, determinate de factori cu actiune continua asupra fenomenului, in timp ce componenta reziduala are caracter aleator fiind efectul actiunii unor factori imprevizibili, accidentali.

Modelul clasic de descompunere a seriilor cronologice este de regula:

aditiv: sau

multiplicativ: 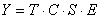respectiv

o combinatie mixta a componentelor seriei.

Tehnicile de analiza, in acest context, au ca obiective:

- separarea fiecarei componente si modelarea comportamentului sau, respectiv

- previziunea evolutiei fiecarei componente, iar apoi compunerea acestora in scopul obtinerii de previziuni privind evolutia fenomenului Y. Principiul de la baza acestei tehnici este descompune pentru a modela iar apoi recompune.

2.3. Estimarea componentei de tendinta

Functii elementare utilizate in modelarea tendintei

Cele mai uzuale functii utilizate pentru modelarea tendintei indicatorilor din economie sunt redate in tabelul 1..

Tabelul 1. Functii elementare utilizate in modelarea tendintei

Stabilirea functiei adecvate pentru modelarea tendintei

In acest scop sunt utile urmatoarele precizari:

• cronograma seriei initiale sau a valorilor netezite sugereaza functiile candidate, numite si linii posibile de tendinta;
• cea mai adecvata functie pentru modelarea tendintei poate fi considerata aceea pentru care se realizeaza minimul sumei patratelor reziduurilor ;
• este adecvata tendinta liniara atunci cand diferentele absolute cu baza in lant     sunt aproximativ constante. De asemenea, precizari specifice in acest sens pentru parabola, exponentiala respectiv hiperbola gasim in tabelul 1.

Estimarea parametrilor tendintei Pentru estimarea parametrilor tendintei liniare

se utilizeaza metoda celor mai mici patrate, expresiile de calcul a parametrilor a, b sunt deci urmatoarele:

sau echivalent

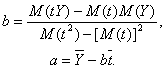
Seria prezinta o tendinta de crestere atunci cand b > 0 respectiv de descrestere daca b < 0.

Cu exceptia curbei logistice, celelalte functii neliniare din tabelul1 pot fi aduse la o forma liniarizata prin anumite substitutii, respectiv prin aplicarea operatiei de logaritmare in cazul functiei exponentiale si a functiei putere.

Exemplu. Estimarea tendintei liniare

Indicele lunar al pretului productiei industriale pentru piata interna, in perioada ianuarie 1999 iunie 2000 baza de comparatie 1996, a avut o tendinta crescatoare:

Cronograma seriei sugereaza prezenta unei tendinte liniare, peste care se suprapune o componenta aleatoare de amplitudine redusa:

Parametrii tendintei se determina din relatiile:

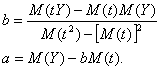
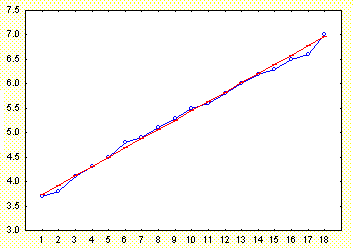
Figura 1. --o-- Indice pret productie industriala;    ------ Tendinta

Exemplificam din calculele intermediare:

rezultand

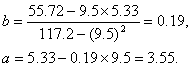
Tendinta seriei se estimeaza prin functia de gradul intai:

al carei grafic este redat in figura 1.

2. Estimarea componentelor deterministe in cazul seriilor sezoniere

Presupunem in acest paragraf ca seria cronologica prezinta tendinta, sezonalitate si o componenta aleatoare. Vom prezenta modul de estimare a tendintei respectiv a componentei sezoniere.

2.1. Modelul de descompunere. Perioada componentei sezoniere

Pentru alegerea modelului de descompunere este indicat a se analiza cronograma seriei.

In general, este adecvat un model aditiv atunci cand amplitudinea oscilatiilor este aproximativ constanta respectiv multiplicativ daca amplitudinea creste sau scade in timp. Frecvent in practica este mai adecvat modelul multiplicativ.

Perioada componentei sezoniere, notata cu p, reprezinta numarul unitatilor de timp din cadrul unui ciclu sezonier. Majoritatea seriilor sezoniere din domeniul economic au durata unui ciclu de un an, p fiind egal cu 4 in cazul datelor trimestriale respectiv 12 in cazul datelor lunare. Prin extensie pot fi studiate si fenomene cu durata unui ciclu mai mica de un an.

2.2. Mediile mobile

Pentru eliminarea componentei sezoniere (desezonalizarea seriei) se aplica datelor o medie mobila de ordin p egal cu perioada componentei sezoniere.

Mediile mobile de ordin p, notate in continuare MM(p), sunt definite de urmatoare relatii:

• daca p este impar , mediile mobile de ordin p sunt

• daca p este par     se definesc analog

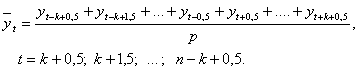
In cazul p par, se introduc mediile mobile centrate de ordin p definite prin:

2.3. Estimarea tendintei in cazul seriilor cu componenta sezoniera

In cazul seriilor sezoniere se intalnesc preponderent in literatura doua modalitati de estimare a tendintei:

desezonalizarea seriei iar apoi estimarea tendintei pornind de la valorile desezonalizate (vezi 2.3.);

modelarea tendintei pornind de la mediile anuale.

2. Estimarea componentei sezoniere

Notatii: t indice pentru an (in general pentru un ciclu sezonier), variind de la 1 la n; s indice pentru sezon, variind de la 1 la p. Modelul de descompunere a seriei are forma:

respectiv

Metoda compararii cu mediile mobile

In cazul modelului multiplicativ

metoda se intalneste in literatura si sub denumire de metoda raportarii la mediile mobile si consta in urmatoarele:

• calculul mediilor mobile de ordin p egal cu perioada componentei sezoniere;
• calculul rapoartelor     ce cuantifica abaterea datelor observate de la tendinta - ciclu. Daca fixam indicele j (ne situam in sezonul j), aceste diferente constituie estimatii pentru ;
• determinarea unui indice mediu pentru fiecare sezon ca o medie a estimatiilor precedente:

aceasta justificandu-se prin necesitatea eliminarii efectului aleator din . Pentru a nu fi afectati de valorile extreme, uneori inainte de calculul mediei, aceste valori se elimina, sau in loc de medie se ia valoarea mediana a estimatiilor ;

• determinarea componentei sezoniere , etapa ce consta intr-o corectie adusa indicilor medii     astfel incat media lor sa fie 1:

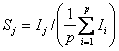
In cazul modelului aditiv

determinarea componentei sezoniere decurge analog.

Exemplu. Estimarea componentelor deterministe in cazul seriilor sezoniere.

Datele privind evolutia trimestriala a productiei de bere din tara noastra (zeci mii hl) in perioada 1996-2001 sunt indicate mai jos

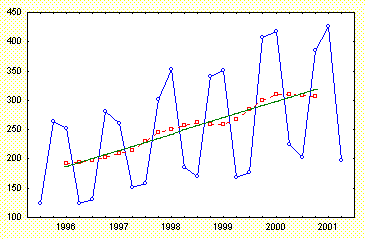
Figura 2. --o-- Productia de bere; -- -- MM(4); ---- Tendinta

a)      Calculul mediilor mobile de ordin p=4

Graficul seriei indica prezenta unei componente sezoniere predominante, de perioada p = Mediile mobile de ordin p = 4 sunt calculate conform relatiei de definitie a mediilor mobile centrate. Astfel, spre exemplu:

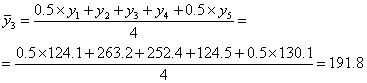
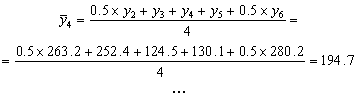
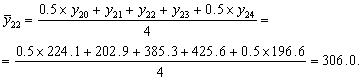
Datele observate au fost numerotate aici in ordine cronologica y₁, y₂, , y₂

Mediile mobile de ordinul 4

b)      Estimarea tendintei pornind de la valorile desezonalizate

Seria mediilor mobile prezentata grafic releva o usoara tendinta de crestere a productiei de bere. Vom considera tendinta liniara:

originea de masurare a timpului trimestrul II al anului 1996, unitatea de masura un trimestru. Astfel, pentru trimestrul III 1996 avem t = 1 s.a.m.d:

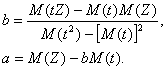
Calcule intermediare:

Tendinta productiei de bere in perioada ianuarie 1996 iunie 2000 este estimata prin:

c) Estimarea componentei sezoniere prin metoda raportarii la mediile mobile

Cum amplitudinea oscilatiilor creste usor in timp, cronograma seriei sugereaza luarea in considerare a unui model multiplicativ:

; iar .

Datele sunt disponibile pentru 6 ani si sunt prezente aici 4 sezoane. Tinand seama de notatiile specifice, reprezinta nivelul productiei de bere in anul i trimestrul j. Astfel, spre exemplu sau . Mediile mobile din tabelul anterior vor fi transpuse intr-un tabel analog cu cel de prezentare a datelor observate:

Rapoartele , respectiv mediile acestora pentru fiecare sezon sunt indicate in tabelul urmator

Calculul indicilor sezonalitatii

Explicatii privind calculele:

, ,

, s.a.m.d.

Cum era de asteptat, aceste rapoarte intre datele observate si mediile mobile sunt mai mici decat 1 pentru trimestrele I si IV, cand nivelul productiei a fost sistematic mai mic (sub tendinta).   

Valoarea medie a acestor indici este 99.6, astfel ca este necesara o corectie astfel incat media sa fie 100:

Urmare a caracterului sezonier specific productiei de bere, in trimestrul I productia a fost mai mica in medie cu 34% decat valorile corespunzatoare de pe tendinta. In trimestrul II productia a fost in medie mai mare de 1.314 ori decat valorile de pe tendinta. Analog se interpreteaza S₃ si S

Componenta sezoniera este data de vectorul format cu indicii sezonalitatii:

S=(S₁, S₂, S₃ , S₄ ) = (0.656; 1.314; 1.340; 0.688).

2.5. Componenta ciclica. Componenta aleatoare

a) Componenta ciclica

Pentru separarea componentei ciclice se poate utiliza metoda compararii cu tendinta. Spre exemplu in cazul modelului multiplicativ:

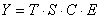
metoda consta in calculul indicilor de ciclicitate. Astfel:

• se estimeaza tendinta printr-o functie elementara. Daca seria prezinta sezonalitate se porneste de la datele desezonalizate sau de la mediile anuale;
• se elimina componenta sezoniera din datele observate, iar apoi se utilizeaza medii mobile in scopul eliminarii si a componentei aleatoare rezultand valorile netezite     (astfel );
• se calculeaza indicii de ciclicitate C_t prin raportare la tendinta:

b) Componenta aleatoare:

in cazul modelului multiplicativ, respectiv

in caz aditiv.

2.6. Previziuni utilizand modelul de descompunere. Masurarea acuratetii previziunilor

a) Previziuni utilizand modelul de descompunere se obtin prin compunerea previziunilor realizate pentru fiecare componenta prezenta in serie, tinand seama de forma modelului:

respectiv .

b) Masurarea acuratetii previziunilor. Daca modelul elaborat conduce la previziunile corespunzatoare datelor , pentru a masura calitatea acestuia de a genera previziuni adecvate se utilizeaza o serie de indicatori sintetici ai erorilor de previziune, cei mai frecvent intalniti fiind:

- eroarea medie patratica:

- eroarea medie absoluta:

- eroarea medie absoluta exprimata procentual:

Exemplu (continuare). Previziunea productiei de bere

Tabelul urmator contine previziunile, datele reale respectiv erorile de previziune privind nivelul productiei de bere.

Prezentam modul de obtinere a rezultatelor anterioare pentru trim. III an 2001. Valorile tendintei respectiv a componentei sezoniere sunt:

(21) = 180.44 + 6.921 = 325.34 respectiv ₃ = 1.3

Modelul de descompunere considerat a fost cel multiplicativ, astfel ca valoarea previzionata este:

iar eroarea de previziune aferenta:

Exemplu (continuare). Previziunea indicelui lunar al pretului productiei industriale.

Avand in vedere tendinta estimata privind evolutia acestui indicator:

T_t = 3.55 + 0.19t

previziunile respectiv erorile de previziune pentru perioada Iulie - Decembrie 2000 sunt indicate mai jos:

Pentru luna Iulie 2000 avem t = 19, extrapolarea tendintei conduce la:

= =3.55 + 0.19 19 = 7.16

= - = 0.2

Alte metode de previziune

a) Previziuni utilizand modele de regresie. Odata estimat si validat, un model de regresie poate fi utilizat pentru previziunea variabilei dependente.

b) Netezirea seriei respectiv previziuni utilizand modele de netezire exponentiala

Varianta simpla a acestei tehnici, in care previziunile sunt obtinute ca o medie ponderata a datelor reprezentand trecutul:

este adecvata previziunii seriilor stationare.

Metoda generalizata in varianta Holt-Winters este adecvata pentru serii cu tendinta si sezonalitate, model multiplicativ. Previziunile sunt date de o functie de previziune local liniara, valorile de pe tendinta liniara fiind corectate cu un indice sezonier aferent sezonului pentru care se realizeaza previziunea.

Atunci cand cronograma seriei nu ofera indicii foarte clare privind prezenta respectiv forma tendintei, este indicat a se utiliza in prealabil o tehnica de netezire ce atenueaza amplitudinea fluctuatiilor aleatoare din serie, scopul fiind evidentierea tendintei. Tehnicile de netezire general utilizate sunt mediile mobile sau tehnicii netezirii exponentiale.

Teme de control. Probleme propuse

Problema 1. Estimarea si extrapolarea tendintei

1.1. Indicele lunar al pretului productiei industriale pentru piata interna, in perioada ianuarie 1999 iunie 2000 baza de comparatie 1996, a avut o tendinta crescatoare:

Se cere: a) estimarea parametrilor tendintei liniare

b) previziunea indicelui lunar al pretului productiei industriale pentru urmatoarele doua luni.

1.2. Datele de mai jos redau evolutia vanzarilor dintr-un produs pe o perioada de 10 luni consecutive:

Se cere: estimarea parametrilor parabolei de tendinta.

1.3. Populatia Romaniei a crescut in perioada 1980-1988 intr-un ritm destul de accelerat, dupa cum arata si datele de mai jos:

Se cere: a) datele confirma ipoteza modelarii tendintei printr-o functie exponentiala?

b) estimarea parametrilor tendintei exponentiale;

c) previziunea populatiei Romaniei pentru urmatorii cinci ani. Comparatii cu valorile reale.

Problema 2. Descompunerea si previziunea seriilor sezoniere

Datele privind evolutia trimestriala a productiei de bere din tara noastra (zeci mii hl) in perioada 1996-2001 sunt indicate in tabelul urmator:

Se cere: a) Estimarea tendintei pornind de la valorile desezonalizate;

b) estimarea componentei sezoniere;

c)determinarea componentei ciclice respectiv aleatoare. Descompunerea seriei pe componente;

d) previziunea productiei de bere pentru urmatoarele patru trimestre.

Problema 3. Determinarea nivelului mediu

3.1. Populatia judetului Cluj la principalele recensaminte a fost:

Se cere: calculul populatiei medii anuale, pe perioada 1930 1992.

3.2. Numarul navelor utilizate in transportul marfurilor in perioada 1991-2000 a inregistrat urmatoarea evolutie:

Se cere: calculul numarului mediu anual de nave utilizate in transportul marfurilor, in perioada considerata.

Problema Determinarea indicelui mediu, ritmului mediu respectiv a diferentei medii

1. Se cunoaste populatia judetului Cluj la ultimele doua recensaminte:

Se cere: indicele mediu anual. Interpretare

2. Productia de biciclete in Romania a scazut dupa 1989:

Se cere: a) calculul indicelui mediu prin metoda autoregresiva

b) ritmul mediu anual. Interpretare.

3. Fondul de locuinte din tara noastra a inregistrat o crestere lenta dupa 1990:

Se cere: calculul si interpretarea diferentei medii absolute.

Problema 5. Cantitatile cumparate q respectiv preturile unitare de cumparare (mii lei) p, pentru 3 produse aflate in consumul populatiei, in doua luni consecutive, au fost:

Se cere: indicii factoriali ai pretului respectiv ai cantitatii prin toate metodele cunoscute. Comparati rezultatele obtinute.

Problema 6. Indicele variatiei integrale si indicii variatiilor factoriale Cunoscand seriile cronologice cu privire la: numarul de someri muncitori (X), numarul de someri cu studii medii (Y), numarul de someri cu studii superioare (Z) din judetul Cluj in 10 luni consecutive, respectiv:

mii persoane

Se cere: a) Relatia matematica ce exprima legatura dintre numarul total de someri (Z) si X, Y, W

b) indicii exprimand variatia integrala a numarului total de someri, calculati cu baza fixa;

c) indicii factoriali de tip Laspeyres, Paasche, Fisher aferenti fiecarui factor care influenteaza numarul total de someri, in ultima luna fata de prima luna.

Bibliografie

1. Buiga A., Dragos C., Lazar D., Parpucea I., Statistica I, Presa Universitara Clujeana, 2003.

2. Florea I., Parpucea I., Buiga A., [1998] , Statistica descriptiva. Teorie si aplicatii, Editura Continental, Alba Iulia, 1998.

3. Florea I., Parpucea I., Buiga A., Lazar D., [2000] , Statistica inferentiala, Presa Universitara Clujeana, Cluj Napoca, 2000.

Melard G., Methodes des prevision a court terme, Ed. de Universite de Bruxelles, 1990.