Sistematizarea si prezentarea datelor statistice

Sistematizarea si prezentarea datelor statistice

Sistematizarea constituie o etapa in cadrul prelucrarii datelor statistice in vederea prezentarii acestora sub forma de serie statistica (tabele statistice).

Datele obtinute ca urmare a procesului de observare statistica, in forma lor bruta, permit o caracterizare amanuntita a fiecarei unitati din populatia considerata. Deoarece, datele rezultate din    observare se prezinta sub forma dezorganizata nu permit o caracterizare a populatiei in ansamblu.

In vederea atingerii scopului cercetarii statistice intreprinse si anume acela de a da o caracterizare de ansamblu a populatiei considerate este necesar ca datele rezultate din observare sa fie supuse unor operatii de sistematizare si prezentare in vederea deducerii a ceea ce este esential, tipic si general in legatura cu populatia.

Deoarece in prelucrarea statistica primul pas il constituie prezentarea datelor observate sub forma de serie (tabel), pentru construirea seriilor statistice se aleg variabilele care trebuie sa fie in stransa dependenta cu scopul cercetarii si cu natura fenomenului cercetat.

Odata precizate variabilele de la baza seriei, se stie care va fi continutul primului sir de date si ca urmare este elucidat criteriul in raport cu care informatiile rezultate din observare vor fi ordonate, necunoscandu-se insa cum se face propriu-zis ordonarea si cum se completeaza primul sir al seriei.

Operatia de stabilire a claselor presupune impartirea unitatilor unei populatii in clase distincte in raport cu una sau mai multe variabile si aranjarea claselor rezultate intr-o anumita ordine. In urma unei asemenea operatii, fiecare unitate trebuie sa se gaseasca in una si numai una din clasele rezultate. Aceasta operatie nu trebuie sa conduca la pierderi de unitati, regasindu-se insa intr-o alta ordine decat cea dupa care s-a realizat observarea.

Omogenitatea constituie o proprietate de baza pe care trebuie sa o aiba clasele. Se spune ca o clasa este omogena daca, pentru unitatile    care fac parte din ea, variabila de grupare inregistreaza variatii nesemnificative.

In cele ce urmeaza se va prezenta operatia de stabilire a claselor in cazul unei serii unidimensionale.

Daca la baza seriei avem o variabila calitativa, atunci clasele se stabilesc in raport cu starile acesteia. Pentru fiecare stare a variabilei se va construi o clasa. Ca urmare, in acest caz, intr-o clasa vor intra toate unitatile care au inregistrat aceeasi stare in timpul observarii in raport cu variabila considerata.

In cazul unei serii care are la baza o variabila cantitativa discreta (numarul starilor nu este prea mare), clasele se stabilesc in mod asemanator ca si la variabilele calitative, respectiv:

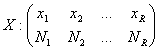
In conditiile in care cercetarea populatiei presupune elaborarea unei serii care are la baza o variabila cantitativa continua sau o variabila cantitativa discreta, dar care in populatia considerata inregistreaza un numar prea mare de stari, clasele nu se mai pot stabili cu ajutorul starilor variabilei. Pentru asemenea cazuri, gruparea unitatilor populatiei in clase se face cu ajutorul intervalelor de grupare (variatie), fiecare interval cuprinzand un numar oarecare de valori ale variabilei. Ca urmare, pentru o serie continua, clasele se definesc cu ajutorul intervalelor de grupare.

Doua probleme se pun in cazul elaborarii unei serii care are la baza o variabila cantitativa continua:

determinarea lungimii intervalelor de variatie;

stabilirea formei de scriere a intervalelor de variatie.

Determinarea lungimii intervalelor de variatie conduce la doua situatii:

serii construire cu intervale de lungime egala;

serii construite cu intervale de lungime diferite.

Stabilirea numarului de intervale de variatie trebuie sa asigure satisfacerea urmatoarelor conditii:

informatia care se pierde in urma operatiei de grupare sa nu fie prea mare, iar populatia sa nu fie prea faramitata in raport cu variabilele de grupare;

media aritmetica a fiecarei grupe (in raport cu valorile inregistrate) sa fie cat mai aproape de centrul intervalului de variatie respectiv;

sa nu existe grupe vide;

reprezentarea grafica a seriei rezultate sa permita conturarea unei regularitati a fenomenului de studiat din cadrul populatiei. Trebuie remarcat ca acest lucru nu este posibil nici in cazul unui numar mic de intervale deoarece se pierd prea multe date, nici in cazul unui numar prea mare de intervale, populatia faramitandu-se prea tare.

Statisticianul american H.A. Struges a stabilit pentru cazul in care populatia in raport cu variabila X este normala, urmatoarea expresie:

(2.1)

(1+3,322 LgN, avand semnificatia de "numar de intervale"), pentru celelalte cazuri rezultatul fiind orientativ, servind la determinarea cu aproximatie a lungimii intervalelor de variatie in cazul in care acestea vor fi de lungime egala. In expresia de calcul a lungimii intervalelor intervine valoarea maxima si cea minima a variabilei, cat si volumul populatiei. In urma stabilirii lungimii intervalelor. Se elaboreaza seria de intervale de lungime egala dupa cum urmeaza:

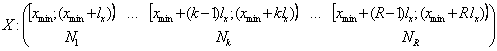
daca se presupune ca au rezultat R intervale, unde N_k, reprezinta volumele claselor in care s-a structurat populatia.

Numeroase sunt cazurile practice in care studiul unei populatii in raport cu o variabila sau mai multe presupune impartirea domeniilor de variatie ale acestora in intervale de lungime neegala. In asemenea cazuri nu exista o relatie de calcul in acest sens. Stabilirea intervalelor de variatie se face in directa legatura cu variatia variabilelor si distribuirea unitatilor in raport cu acestea.

Daca la baza seriei in cauza stau doua sau mai multe variabile calitative sau cantitative atunci clasele se stabilesc in raport cu fiecare din variabilele considerate prin starile acestora (vezi seria 1.5), avem serii bidimensionale sau multidimensionale.

Nu este recomandat ca numarul variabilelor in raport cu care se studiaza populatia sa fie prea mare, deoarece aceasta duce la o divizare exagerata a populatiei pierzandu-se din vedere aspectele principale.

Dupa ce clasele au fost definite, are loc repartizarea unitatilor populatiei in clasele respective, folosind in acest scop un algoritm adecvat.

Pentru elaborarea si prezentarea seriilor statistice se apeleaza la pachete de programe statistice cum ar fi: S.P.S.S. (Statistical Package for the Social Sciences), STATISTICA, S.A.S. (Statistical Analysis System), STATGRAPHICS, etc.