vDINAMICA SISTEMELOR CU 1 GLD. VIBRATII LIBERE CU AMORTIZARE. FRACTIUNE DIN AMORTIZAREA CRITICA. DECREMENT LOGARITMIC AL AMORTIZARII

Dinamica sistemelor cu 1 GLD. Vibratii libere cu amortizare. fractiune din amortizarea critica. decrement logaritmic al amortizarii

In situatia in care sistemul oscilant poseda capacitate de amortizare, miscarea inceteaza dupa un anumit interval de timp, avand deci caracterul unei vibratii tranzitorii. In ecuatia de echilibru dinamic instantaneu care va caracteriza miscarea sistemului, intervin urmatoarele forte: (i) forta de inertie, ; (ii) forta de rezistenta (de amortizare vascoasa) (iii) forta elastica, . Ecuatia de miscare a sistemului dinamic rezulta de forma:

Pentru rezolvarea acestei ecuatii diferentiale omogene de ordinul II cu coeficienti constanti se scrie ecuatia caracteristica: ale carei radacini sunt: . In functie de valoarea discriminantului din relatia anterioara se disting 3 cazuri care vor fi analizate in continuare.

amorizare critica

Valoarea coeficientului de amortizare pentru care discriminantul se anuleaza se numeste coeficient de amortizare critica si se noteaza prin c_cr. Rezulta deci:

, adica cum

Se constata ca coeficientul de amortizare crititca este o caracteristica proprie a sistemului oscilant, exprinmandu-se prin intermediul elementelor acestuia. Rapostul dintre coeficientul de amortizare efectiv si cel de amortizare critica se numeste fractiune din amortizarea critica si se noteaza cu ν.

sau

Fractiunea din amortizarea critica are o larga utilizare in Dinamica structurilor si in special in Ingineria seismica. Spre deoasebire de , fractiunea din amortizarea critica este un numar adimensional si caracterizeaza mult mai intuitiv capacitatea de amortizare a unei structuri. Prin urmare, in cazul amortizarii critice rezulta:

sau

Intrucat solutia ecuatiei de miscare va avea expresia:

Constantele de integrare A si B se determina din conditiile initiale ale miscarii: si , obtinandu-se: si si deci .

Relatia anterioara arata ca miscarea corespunzatoare acestui caz este aperiodica, pierzandu-si caracterul oscilatoriu.

amorizare supracritica

Daca coeficientul de amortizare efectiv c depaseste valoarea coeficientului de amortizare critica c_cr se considera ca sistemul oscilant are amortizare supracritica. Deci cand: rezulta si , iar radacinile r₁ si r₂ sunt reale si negative . Solutia ecuatiei de miscare rezulta de forma:

In baza conditiilor initiale se obtin expresiile constantelor, A si B:

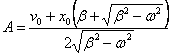si

Analog cazului precedent, miscarea rezultanta nu mai este oscilatorie ci aperiodica. Intr-o miscare aperiodica, sistemul care a fost scos din pozitia de echilibru revine la pozitia sa initiala fara a oscila.

amorizare subcritica

Acest ultim caz intereseaza din punct de vedere practic intrucat , si . Radacinile ecuatiei caracteristice vor fi de aceasta data imaginare (complexe conjugate), adica:

sau

unde 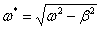reprezinta pulsatia proprie a sistemului oscilant cand se tine seama de influenta amortizarii si .

In acest caz solutia ecuatiei de miscare este de forma:

Dezvoltand functiile exponentiale si utilizand relatiile lui Euler, solutia de mai sus se poate scrie sub forma:

Prin compactarea termenilor din paranteza, se obtine:   

unde: si .

Constantele si se obtin din conditiile initiale, folosindu-se deci si expresia variatiei vitezei:

Rezulta:    si

Exprimarea miscarii prin intermediul relatiei este mult mai convenabila si mai sugestiva. Aceasta este o miscare armonica de pulsatie si amplitudine care descreste in timp. O asemenea miscare se mai numeste si pseudo-armonica.

Studiul miscarii permite identificarea completa a caracteristicilor de definire (valoare proprie, amortizare) ale sistemului dinamic.

Pulsatia proprie a vibratiei este influentata de amortizare prin coeficientul sau prin factorul :

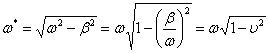
Se observa ca pulsatia proprie, cand se tine cont de prezenta amortizarii, este mai mica decat in cazul cand se neglijeaza amortizarea. In baza relatiei anterioare se pot determina urmatoarele expresii:

Deoarece pentru structurile frecvent utilizate in constructiile ingineresti fractiunea din amortizarea critica este mai mica de 20%, se poate neglija influenta amortizarii asupra valorii proprii a sistemului dinamic, astfel incat relatiile anterioare devin:

decrementul logaritmic

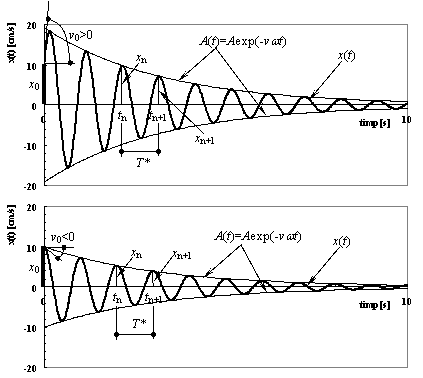
Decrementul logaritmic al amortizarii reprezinta logaritmul natural al raportului dintre doua amplitudini succesive decalate printr-o perioada. Se considera urmatoarele amplitudini succesive ale vibratiei, si , al caror raport este:

Conform definitiei, decrementul logaritmic rezulta:

Cu ajutorul relatiei anterioare se determina valoarea fractiunii din amortizarea critica care se foloseste in calculul dinamic. Relatia de calcul poate fi:

in cazul amortizarii vascoase, valoarea fractiunii din amortizarea critica depinde in general de tipul structurilor si de materialul din care acestea sunt executate si se obtine numai pe cale experimentala.