| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
Lesson Title: Fourier representation of a periodic pulse-train
Lesson Number: 05
|
|
![]()
Background:
In Chapter 3, the Fourier representation (analysis) of a periodic signal was developed. The basis functions were defined to be the complex exponential basis functions
, k=[0 ,1 , , ¥]
which form an orthogonal set. The synthesis formula (Eq. 3.27) is given by:
![]()
where the analysis formula satisfies:
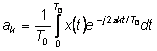
which defines the amplitude of the kth harmonic which is physically at frequency fk = k f0, where f0= 1/T0 with T0 being the fundamental period. Using Eulers equation, that states that
ejf(t) = cos(f(t)) + j sin(f(t))
the Fourier series can, if desired, be expressed in terms of cosines and series.
Challenge:
In Section 3.6.1, the Fourier series of a periodic pulse was derived. Specifically, for a continuous-time signal x(t) having the waveform (called 50% duty cycle):
 1.0
1.0
-2T0 -T0 0 0.5T0 T0 2T0
Figure 1: Periodic pulse train.
The Fourier coefficients are computed as follows for k¹0:
 (imaginary)
(imaginary)
since e-j2p=1 and e-jp=-1, ak = 0 if k is even (k¹0) and ak = 1/jpk if k is odd. For k=0, however
The magnitude spectrum is given in Figure 3-16 and interpreted below, assuming T0=1/25.

-175 -75 -25 0 25 75 175
Figure 2: Magnitude spectrum of the signal shown in Figure 1.
What if T0 ¥. What is the resulting Fourier series and magnitude spectrum. Does it make sense?
Consider the slightly modified version of x(t) shown below. Predict the resulting spectral representation.
![]() 0.5
0.5
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() -0.5
-0.5
-2T0 -T0 0 0.5T0 T0 2T0
Figure 3: Modified 50% duty cycle periodic pulse train.
Consider another modified version of x(t) shown below. Predict the resulting spectral representation and validate with formal computation?
 1.0
1.0
-2T0 -T0 0 T0 2T0
Figure 4: Modified 50% duty cycle periodic pulse train.
The analysis requested in Question 3 relates to the analysis equation. How could you demonstrate that the answer makes sense in the context of the synthesis equation?
Response:
Q. What if T0 ¥. What is the resulting Fourier series and magnitude spectrum. Does it make sense?
A. Based on the previous analysis, in the limit a0=1 and ak 0 for all k¹0. The first harmonic is located at f1=¥. However, even though the signal x(t) has a value of unity for tI[0, ¥), the DC value of the signal remains one-half. This can be justified on the basis that x(t) also has a value of zero for tI(-¥, 0), that is half-on, half-off.
Q. Consider the slightly modified version of x(t) shown below. Predict the resulting spectral representation.
![]()
![]()
![]()
![]() 0.5
0.5
![]()
-0.5
-2T0 -T0 0 0.5T0 T0 2T0
A. The essential difference is the signal DC bias of ½. The Fourier transform of the modified signal is therefore given by ak = 0 for k is even, k¹0, and ak = 1/jpk if k is odd, and a0 = 0 (DC).
Q. Consider another modified version of x(t) shown below. Predict the resulting spectral representation and validate with formal computation?
 1.0
1.0
-2T0 -T0 0 T0 2T0
A. The modified signal is equal to the original x(t) shift in time by T0/4 seconds. The Fourier coefficients can be computed as shown below. For k¹0:
 which also introduces the classic sin(x)/x or sinc(x) function. The DC term is computed to
be:
which also introduces the classic sin(x)/x or sinc(x) function. The DC term is computed to
be:
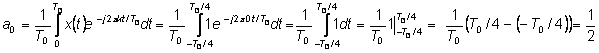
as before. The coefficients ak can then be computed to be ak = with all the even coefficients (except a0) having a value of zero.
The synthesis equation, therefore, is given by

which simplifies to
![]()
The magnitude response is sketched below (based on the exponential form):

-175 -75 -25 0 25 75 175
which is identical to that shown in Figure 2. The signals associated with these two graphs therefore identical. Well, no. While agreeing in magnitude response, the phase responses are 90 apart. The 90 difference is due to the T0/4 temporal delay between the two signals.
Q. The analysis requested in Question 3 relates to the analysis equation. How could you demonstrate that the answer makes sense in the context of the synthesis equation?
A. Using a general purpose computer, the signal x(t) described by the synthesis equation can be generated and displayed. The following MatLab program was created and executed. The results are shown below.
% cosine coefficients
a0 = 0.5 * ones(1,100);
a1 = (2/pi) * ones(1,100);
a3 = -(2/(3*pi)) * ones(1,100);
a5 = (2/(5*pi)) * ones(1,100);
% pure sinusoids
x0 = ones(1,100);
n = 0:99;
x1 = cos(2*pi*0.01*n);
x3 = cos(2*pi*0.03*n);
x5 = cos(2*pi*0.05*n);
figure
plot(n,x0,n,x1,n,x3,n,x5);
figure;
subplot(1,4,1)
% construct time-domain signal
y0 = a0.*x0;
plot(n,y0);
y1=y0+a1.*x1;
subplot(1,4,2)
plot(n,y1);
y3=y1+a3.*x3;
subplot(1,4,3)
plot(n,y3);
y5=y3+a5.*x5;
subplot(1,4,4)
plot(n,y5);
x5(t) x3(t) x1(t) x0(t)
![]()
![]()
![]()
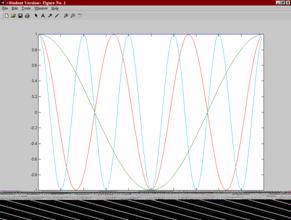
(Left) First three non-zero harmonics (f1=0.5, f3=1.5, f5=2.5), (Right) Constructed cosine series reconstruction starting with x0(t)=a0cos(0t)= a0, x1(t)= x0(t)+a1cos(0.5t), x3(t)= x1(t)+a3cos(1.5t), x5(t)= x3(t)+a5cos(2.5t). The data suggested that xi(t) is converging to a periodic pulse train with period T0=2. The ringing appearing on the rightmost graph is due to what is called Gibbs phenomenon.
Motivation: The production of frequency-domain representation of periodic continuous-time signals has been presented and exemplified. However, because the Fourier coefficient production rules are based on calculus (integration), the analysis technique does not easily lend itself to analysis by a general-purpose digital computer. Discrete-time signals, however, do admit digital computer analysis. The theory upon which the discrete-time signals are created, called the Sampling Theorem, is the logically the next topic of study.
References:
Principles of Signals and System, F. Taylor, McGraw Hill, 1994
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2113
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved