| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|||
|
|||
Applications
of the
Part One: Analysis of Network (6-2, 6-3)
Review of Resistive Network
Elements
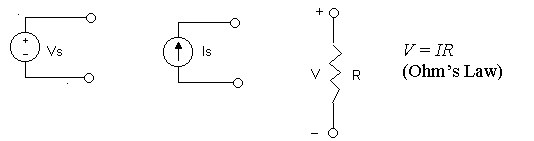
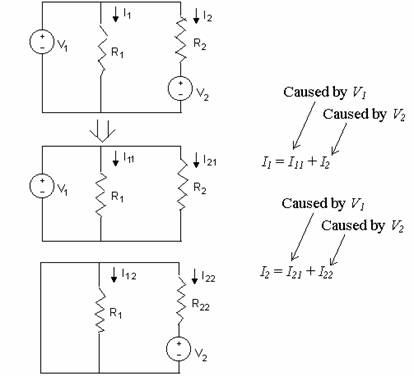
2) Superposition
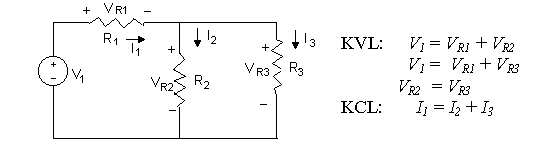
3) KVL and KCL
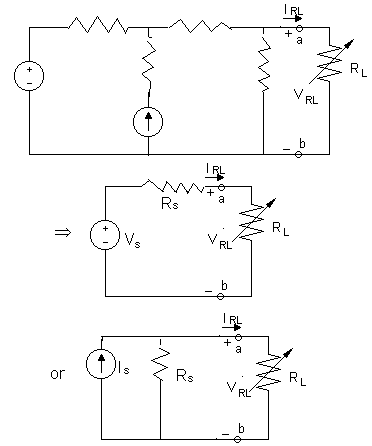
4) Equivalent Circuits
5) Nodal Analysis and Mesh Analysis
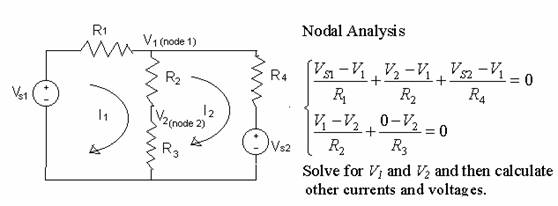
Mesh analysis
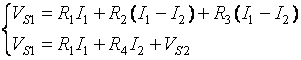 Solve for I1 and I2.
Solve for I1 and I2.
Characteristics of Dynamic Network
Dynamic Elements Ohms Law: ineffective
1) Inductor
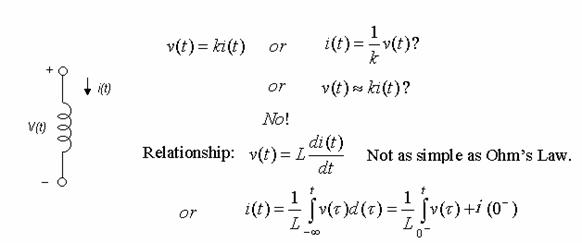
Capacitor
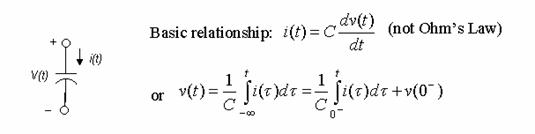
3) Example (Problem 5.9):
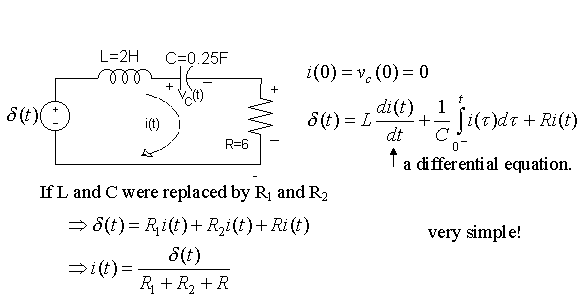
Why so simple? Algebraic operation!
Dynamic Relationships (not Ohms Law) Complicate the analysis
Using
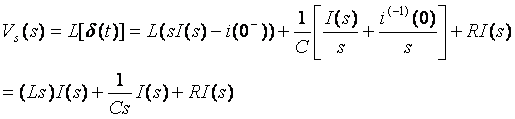
Define Generalized Resistors (Impedances)
![]()
![]()
![]()
![]()
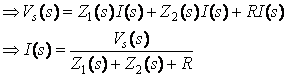 As simple as
resistive network!
As simple as
resistive network!
Solution proposed for dynamic network:
All the dynamic elements Þ Laplace Trans. Models.
Þ  As Resistive Network
As Resistive Network
Key:
Capacitor

Important: We can handle these two resistive network elements!
2) Inductor
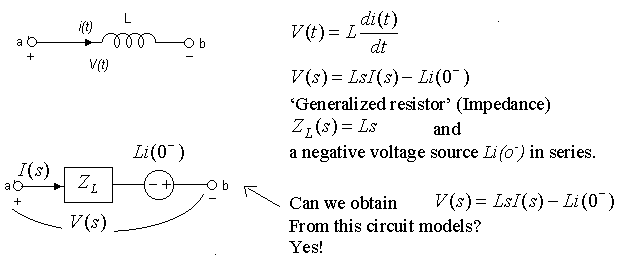
3) Resistor V(s) = RI(s)
4)Sources
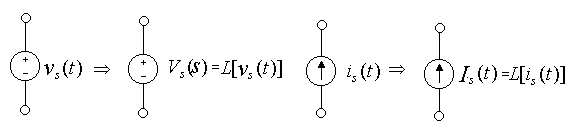
Mutual Inductance (Transformers)
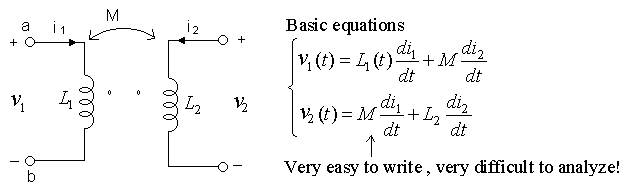
(make sure both i1 and i2 either away
or toward the polarity marks to make
the mutual inductance M positive.)
Circuit (not transformer) form:
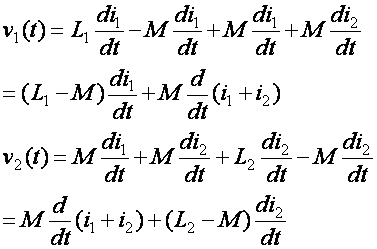
Benefits of transform
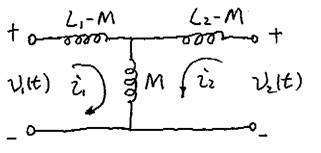 Lets write the equations from this circuit form:
Lets write the equations from this circuit form:
![]()
The Same
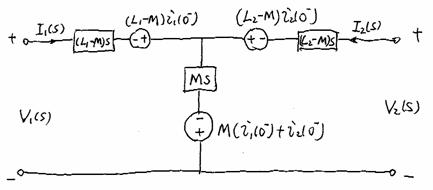
Just sources and generalized resistors (impedances)!
Circuit Analysis: Examples
Key: Remember very little, capable of doing a lot
How: follow your intuition, resistive network
Little to remember: models for inductor, capacitor and mutual inductance.
Example 6-4: Find Norton Equivalent circuit
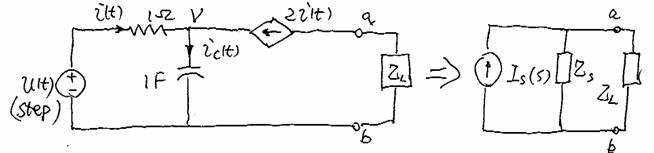
Assumption: ![]()
*Review of Resistive Network
1) short-circuit
current through the load: ![]()
2) Equivalent
Impedance or Resistance ![]() or
or ![]() :
:
A: Remove all sources
B: Replace ![]() by an external source
by an external source
C: Calculate the current generated by the external source point a
D: Voltage /
Current Þ ![]()
*Solution
1) Find ![]()
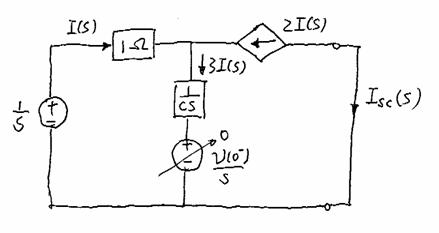
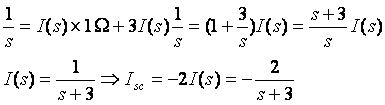
2) Find ![]()
Vtest(s)
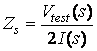
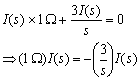
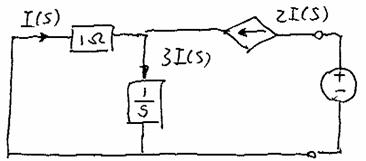
(Will
I(s) be zero? We dont know yet!)
condition: 1 ohm = 3/s
or I(s) = 0
=>I(s) = 0 =>Zs ¥
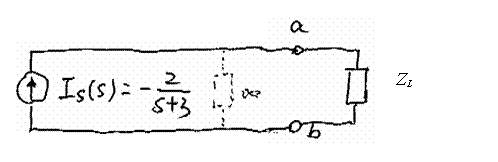
Example 6-5: Loop Analysis (including initial condition)
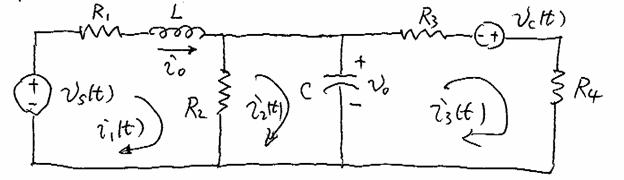
Question: What are i0 and v0?
What is ![]() ?
?
|

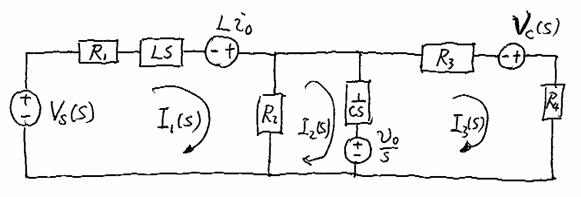
Why
this direction?
KVL Equations
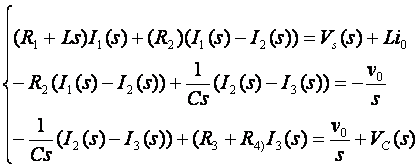
Important: Signs of the sources!
Simplified (Standard form)
![]()
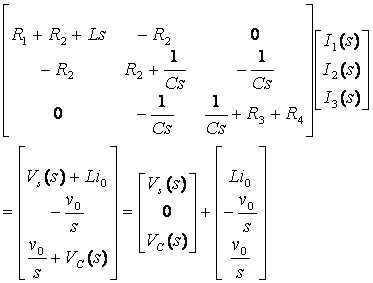
Transfer Functions
Definition of a Transfer Function
Definition
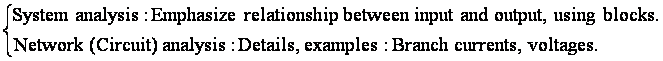
System analysis: How the system processes the input to form the output, or

Input : variable used and to be adjusted
to change or influence the output.
Can you give some examples for input and output?
Quantitative Description of how the system processes
the input to form the output: Transfer Function H(s)
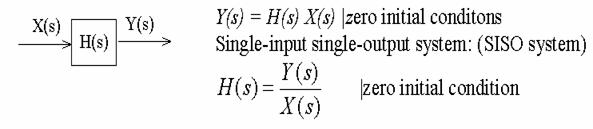
d input
The resultant output y(t) to d (t) input: unit impulse response
In this case: X(s) = L [d (t)] =
Y(s) = Laplace Transform of the unit impulse response
=> H(s) = Y(s)/X(s) = Y(s)
Therefore: What is the transfer function of a system?
Answer : It is the
of the system.
Facts on Transfer Functions
* Independent of input, a property of the system structure and parameters.
* Obtained with zero initial conditions.
(Can we obtain the complete response of a system based on its transfer
function and the input?)
* Rational Function of s (Linear, lumped, fixed)
* H(s): Transfer function
H( j2pf ) or H( jw : frequency response function of the system
(Replace s in H(s) by j2pf or jw
|H( j2pf )| or |H( jw |: amplitude response function
ÐH(j2pf) or ÐH( jw Phase response function
Properties of Transfer Function for Linear, Lumped stable systems
Rational Function of s
Lumped, fixed, linear system =>
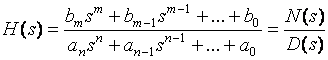
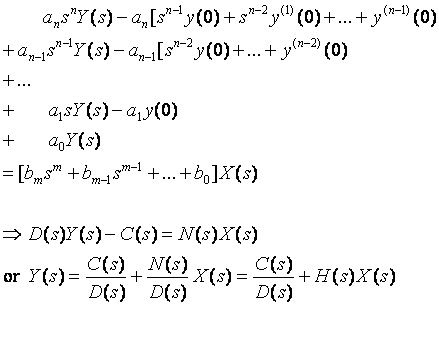
Corresponding differential equations:
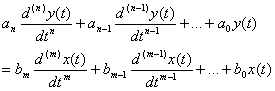
(2) ![]() all real! Why? Results from real system
components.
all real! Why? Results from real system
components.
Roots of N(s), D(s): real or complex conjugate pairs.
Poles of the transfer function: roots of D(s)
Zeros of the transfer function: roots of N(s)
Example: 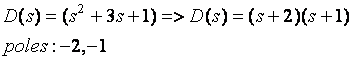
(3) H(s) = N(s)/D(s) of bounded-input bounded-output (BIBO) stable
system
* Degree of N(s) £ Degree of D(s)
Why? If degree N(s) > Degree D(s)
 where degree N (s) <degree D(s)
where degree N (s) <degree D(s)
Under a bounded-input x(t) = u(t) => X(s) = 1/s
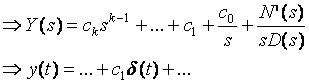 (
(![]() not bounded!)
not bounded!)
* Poles: must lie in the left half of the s-plan (l. h. p)
i.e., 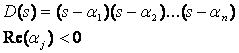
Why?
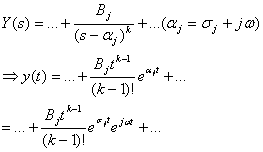
(Can we also include k=1 into this form? Yes!)

* Any restriction on zeros? No (for BIBO stable system)
Components of System Response
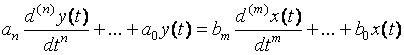
Because x(t) is input, we can assume
![]()

D(s): System parameters
C(s): Determined by the initial conditions (initial states)
Initial-State Response (ISR) or Zero-Input Response (ZIR):

Zero-State Response (ZSR) (due to input)
![]()
From another point of view:
Transient Response: Approaches zero as tà
Forced Response: Steady-State response if the forced
response is a constant
How to find (1) zero-input response or initial-state response? No problem!
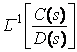
(2) zero-state response? No prolbem!
![]()
How to find (1) transient response? All terms which go to 0 as tà¥
(2) forced response? All terms other than transient terms.
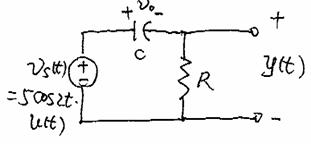 Example 6-7
Example 6-7
Input ![]()
Output ![]()
Initial capacitor
voltage: ![]()
RC = second
Find total response
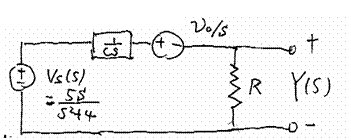

Find zero-input response and zero-state response
Zero-input response: 
Zero-state response:
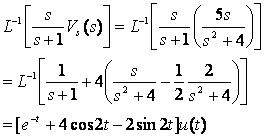
Find transient and forced response
![]()
Which terms go to zero as tà¥
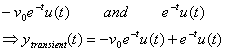
What are the other terms:
Asymptotic and Marginal Stability
System: (1) Asymptotically stable if ![]() as tॠ(no input) for all
as tॠ(no input) for all
possible initial conditions, y(0), y(0), y(n-1)(0)
è Internal stability, has nothing to do with external input/output
(2) Marginally stable
![]() all t>0 and
all initial conditions
all t>0 and
all initial conditions
(3) Unstable
![]() grows without bound for at least some values
grows without bound for at least some values
of the initial condition.
(4) Asymptotically stable (internally stable)
=>must be BIBO stable. (external stability)
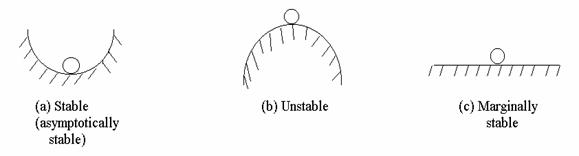
6-5 Routh Array
1. Introduction
System H(s) = N(s)/D(s) asymptotically stable all poles in l.h.p (not
include jw axis.
How to determine the stability?
Factorize D(s):
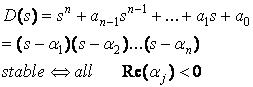
Other method to determine (just) stability without factorization?
Routh Array
Necessary condition
All ![]() (when
(when ![]() is used)
is used)
ð any ![]() => system unstable!
=> system unstable!
Why?
Denote ![]() to esnure stability
to esnure stability
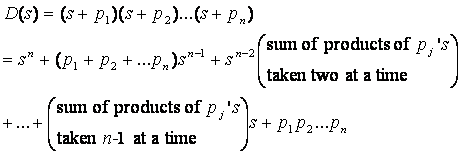
When all Re(pj) > 0 , all coefficients must be greater than zero. If some coefficient is not greater than zero, there must
be
at least a Re(pj) <= 0 (i.e.,
![]() )
)
=> system unstable
Routh Array
Question: All ![]() implies system stable?
implies system stable?
Not necessary
Judge the stability: Use Routh Array (necessary and sufficient)
2. Routh Array Criterion
Find how many poles in the right half of the s-plane
Basic Method
![]()
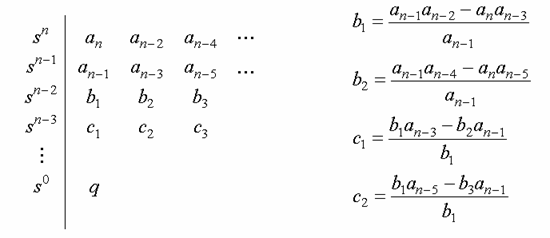
Formation of Routh Array
Number of sign changes in the first column of the array
=> number of poles in the r. h. p.
Example 6-8
![]()
![]()
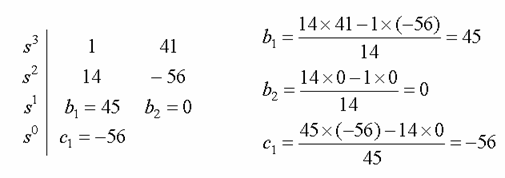
sign: Changed once =>one pole in the r.h.p
verification:
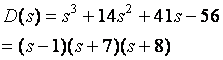
Example 6-9
![]()
![]()

Sign: changed twice => two poles in r.h.p.
Modifications for zero entries in the array
Case 1: First element of a row is zero
ð replace 0 by ε (a small positive number)
Example 6-10
![]()
![]()

Case 2: whole row is zero (must occur at odd power row)
construct an auxiliary polynomial and the perform differentiation
Example: best way.
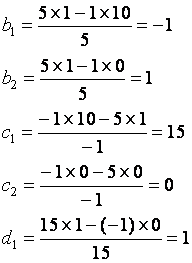
Example 6-11
S
![]()
![]()
![]()
![]()
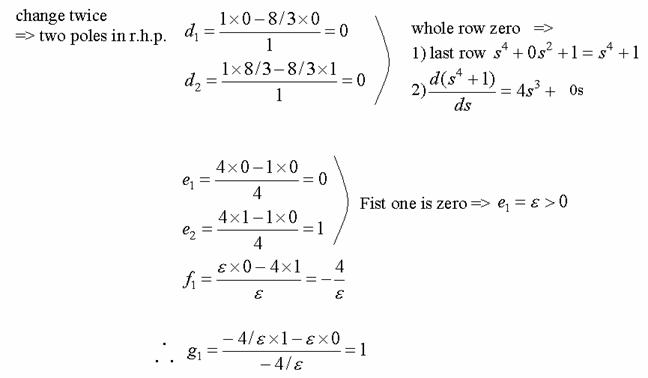
Application: Can not be replaced by MatLab
Range of some system parameters.
Example:
![]()
![]()
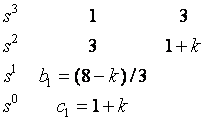
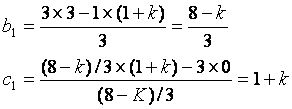
Stable system
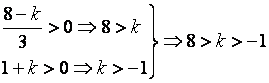 to ensure system
stable!
to ensure system
stable!
Frequency Response and Bode Plot
Transfer Function 
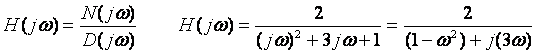
Why?
![]()
![]() Amplitude Response:
Amplitude Response: 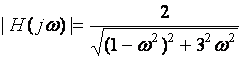
Real positive number: function of ![]()
Phase Response: 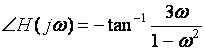
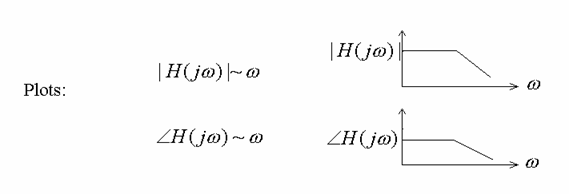
Interest of this section
In particular, obtain
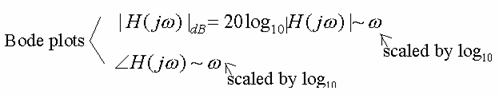
![]()

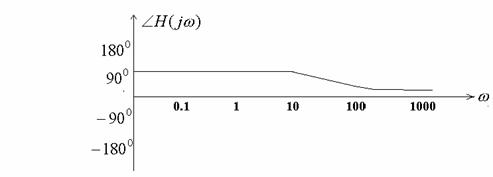
Asymptotes only!
Bode plots of factors
Constant factor k:
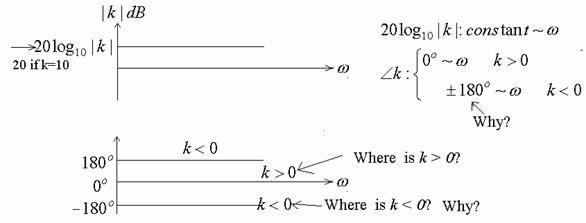
(2) s
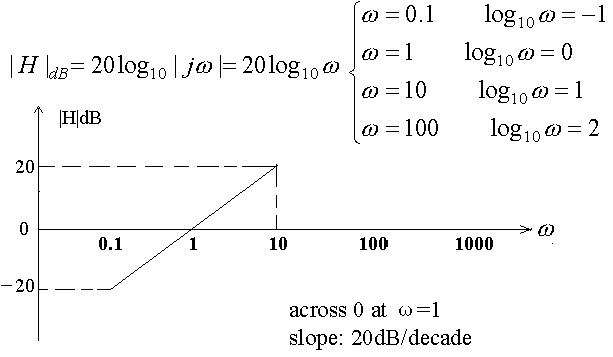

Can we plot it?
![]() : Can we plot
: Can we plot ![]() for them?
for them?
Phase s:![]()
![]() :
: ![]()
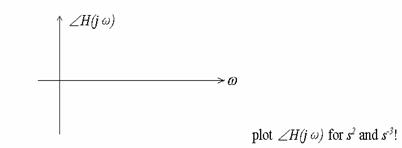
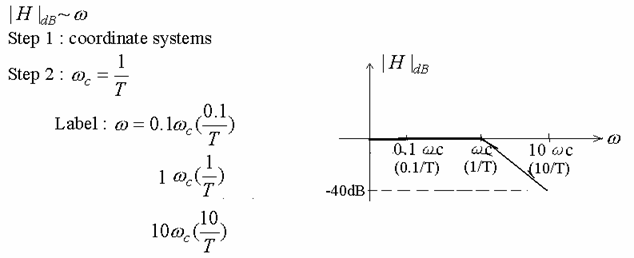
(3) ![]()
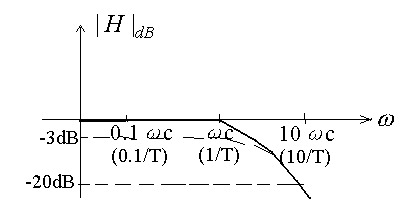
step 1: Coordinate systems
step 2: corner frequency
![]()
step 3: Label 0.1wc wc wc
Line
![]()
step 4: left of wc :
Point 1
![]()
![]()
![]()
Point
2![]()
step 5: right of wc :
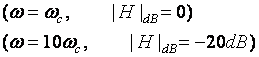
Why?
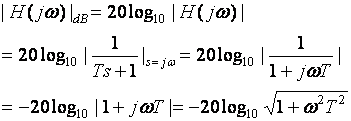
If
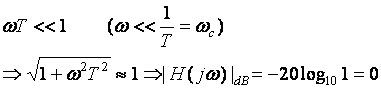
If
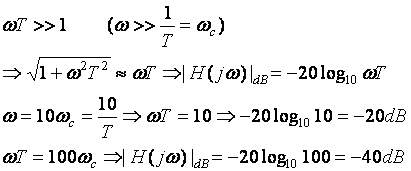
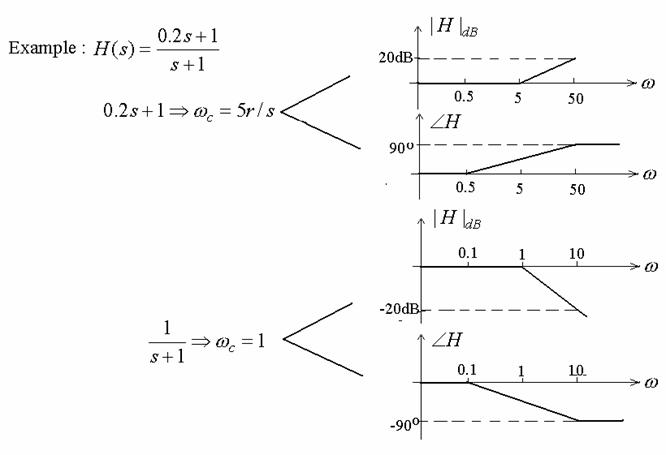
Example: ![]()
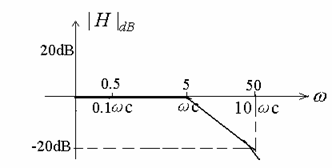 What is T : T = 0.2
What is T : T = 0.2
What is wc wc = 1/T = 5
Example : 0.2s + 1
Example : (0.2s + 1)2, (0.2s + 1)-2
Example : (Ts + 1)N
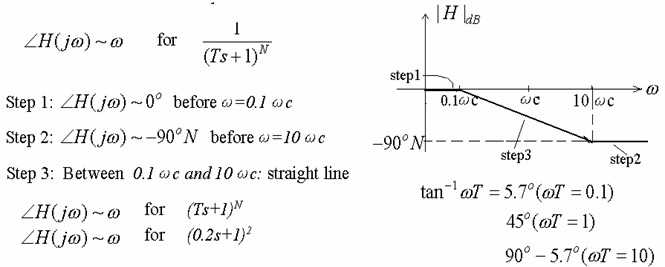
(4) ![]() (Complex --- Conjugate poles)
(Complex --- Conjugate poles)
Step 3 : Before ![]() :
: ![]()
Right of ![]() :
:
Line
![]() point 1: (
point 1: (![]() ,
, ![]() )
)
![]() point 2: (
point 2: (![]() ,
, ![]() )
)
Example: ![]()
Actual ![]() and z (show Fig
6-20)
and z (show Fig
6-20)
Whats resonant
frequency: reach maximum: 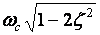
Under what condition we have a resonant frequency:
![]()
![]() : see fig 6-21
: see fig 6-21
What about : ![]() ?
?
Bode plots: More than one factors
Can we sum two ![]() plots into one?
plots into one?
Can we sum two ![]() plots into one?
plots into one?
Yes!
MatLab
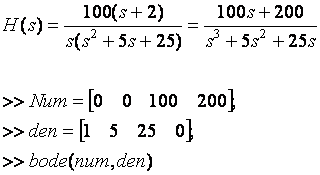
Show result in fig 6-24
6.7 Block Diagrams
What is a block diagram?
Concepts: Block, block transfer function,
Interconnection, signal flow, direction
Summer
System input, system output
Simplification, system transfer function
Block
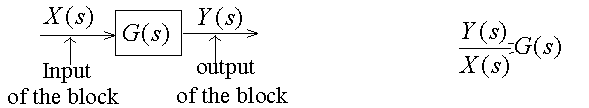
Assumption: Y(s) is determined
 by input (X(s)) and block transfer
by input (X(s)) and block transfer
function (G(s)). Not affected by
the load.
Should be vary careful in
analysis of practical systems about the accuracy of this assumption.
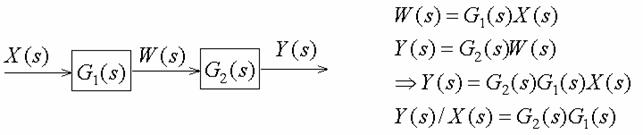
Cascade connection
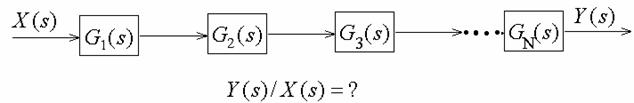
Summer
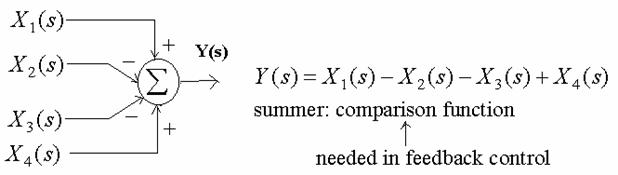
5. Single-loop system
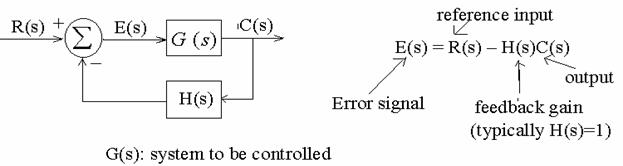
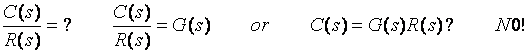
![]()
![]()
![]()
Lets find ![]()
![]() Closed-loop
transfer function
Closed-loop
transfer function
Equation (1) ![]()
![]()
Equation (2) ![]()
![]()
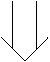
![]()
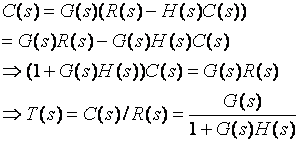
6. More Rules and Summary: Table 6-1
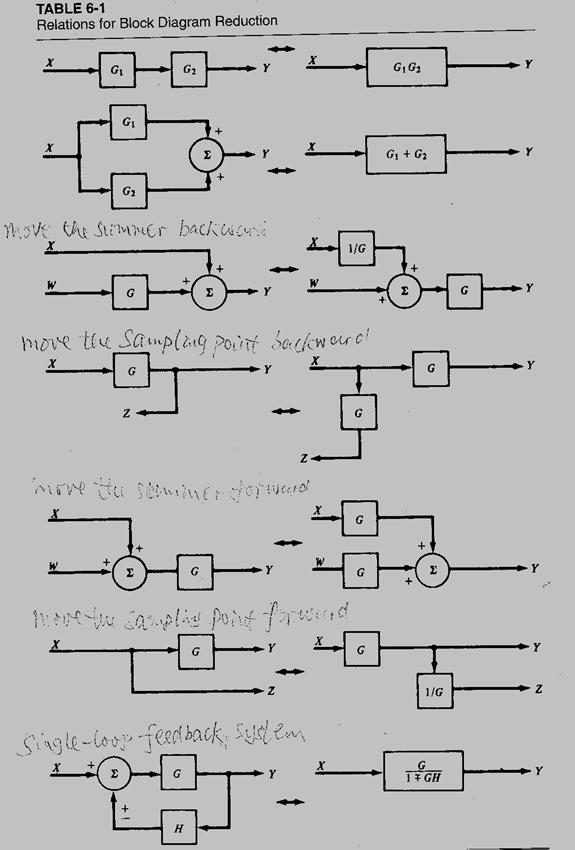
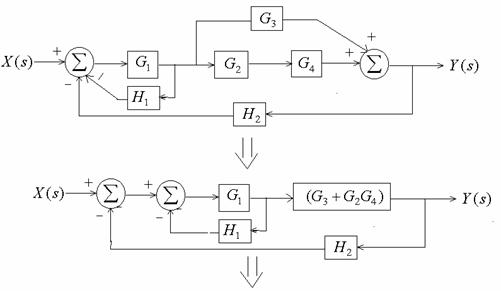
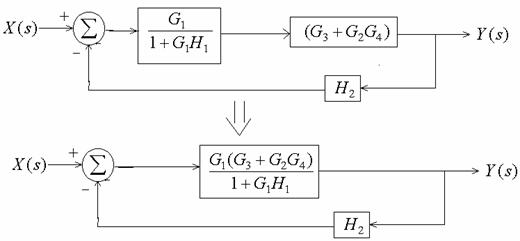
Example 6-14: Find Y(s)/X(s)
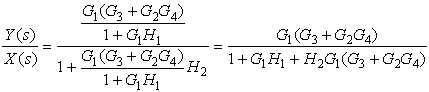
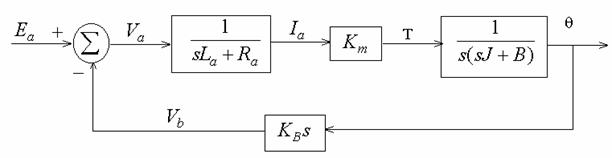
Example 6-15: Armature- Controlled dc servomotor
Input : Ea (armature voltage)
Output : ![]() (angular shift)
(angular shift)
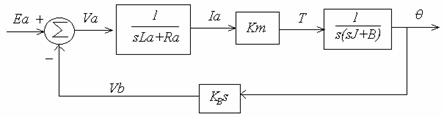
Can we obtain ![]() ?
?
Example 6-16 Design of control system
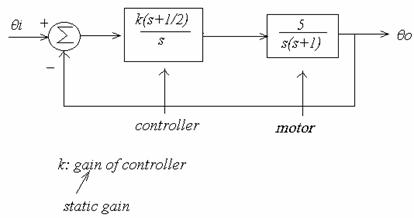
Design of K such that closed loop system stable.
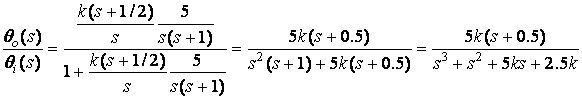
Routh Array: ![]()
![]()
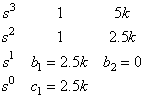
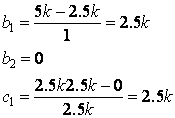
System stable if k>0. If certain performance is required in addition to the stability, k must be further designed.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2163
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved