| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
Wahrscheinlichkeitsrechnung
Begriffe:
z.B. Würfel: S=
E Ì S ist ein Ereignis
P(S) ist die Menge der Ereignisse (P=Potenzmenge)
E=S ist ein sicheres Ereignis
E==Æ ist das unmögliche Ereignis
Wenn E Ì S ein Ereignis ist, dann ist S E = ![]() das
Gegenereignis zu E bzgl .S:
das
Gegenereignis zu E bzgl .S:
![]()
![]() = S E
= S E ![]() = Æ
= Æ
Definition der Wahrscheinlichkeit W:
W: P(S) (W ist eine Funktion von P von S auf das Intervall 0 und 1)
W(S) = 1
W(Æ
Wenn E1,,En paarweise disjunkte Ereignisse sind, dann gilt:
W(E1 E2 En) = W(E1) + W(E2) + + W(En)
Wenn die Menge der Elementarereignisse endlich ist und das Auftreten der Elementare gleich wahrscheinlich ist, dann ist W folgendermaßen definiert:
![]()
Gegenereignis:
W(E) = 1-W(![]() )
)
Unabhängigkeit von Ereignissen:
Zwei Ereignisse A und B heißen genau dann unabhängig voneinander, wenn
W(A B) = W(A B) = W(A) W(B)
Eine Permutation einer endlichen Menge m ist eine bijektive Abbildung der Menge auf sich.
Bsp: M=
![]() d identische Permutation: d
d identische Permutation: d
d d
d d
Ist m eine Menge mit n Elementen, dann existieren genau Pn = n!
Binominalkoeffizienten
![]() zahllose Zusammenhänge
zahllose Zusammenhänge
![]() =
=
![]() n ³ k; n,k I N
n ³ k; n,k I N
![]() =
= ![]()
![]() =
= ![]() = 1
= 1
![]() = 1
= 1
![]() = 1
= 1
![]() =
= ![]() = n =
= n = ![]()
Es sei eine Menge von n Elementen gegeben. Jede Auswahl von k Elementen unter Berücksichtigung der Anordnung ist eine Variation ohne Wiederholung.
Hier gilt folgender Satz:
Vn(k) = n (n-1) (n-2), , (n-k+1) = ![]() = k!
= k!
![]()
Bsp: M = , k £ n (a1,a3,a9) ¹ (a3,a1,a9)
Es sei eine Menge von n Elementen gegeben. Jede Auswahl von k Elementen unter Berücksichtigung der Reihenfolge, wobei jedes Element bis zu k-mal auftreten darf, ist eine Variation mit Wiederholung.
Hier gilt folgender Satz:
![]() n|k|
= n n n n = nk
n|k|
= n n n n = nk
Eine Auswahl aus k Elementen aus n Elementen (n ³ k) ohne Berücksichtigung der Reihenfolge heißt Kombination ohne Wiederholung.
Hier gilt folgender Satz: Kn(k) = ![]()
Eine Auswahl aus k Elementen aus n Elementen (n ³ k) ohne Berücksichtigung der Reihenfolge, wobei jedes Element bis zu k-mal ausgewählt werden kann, heißt Kombination mit Wiederholung.
Hier gilt folgender Satz: ![]() n(k) =
n(k) = ![]()
Bernoullisches Versuchsschema
Bsp: In einem Glaskasten befinden sich n Bienen. Wie hoch ist die Wahrscheinlichkeit bei einer virtuellen Trennung des Glaskastens in zwei Teile, dass sich k Bienen im rechten Teil aufhalten? Voraussetzung: Die Bienen bewegen sich unabhängig voneinander)
Wrechts = p
Wlinks = p-1
Wn(k) = ![]() pk (1-p)n-k
pk (1-p)n-k
Bedingte Wahrscheinlichkeit
Es gibt n mögliche Fälle. Dabei gibt es l günstige Fälle für ein Ereignis B. Unter diesen l Fällen sind k günstige Fälle für ein Ereignis A. Wie groß ist die Wahrscheinlichkeit für A und B (dass beide zutreffen)?
W (A B) = ![]()
W (B) = ![]()
W (A| unter der
Bed., dass B eingetreten ist) = W
(A|B) = ![]() =
= ![]()
Definition:
Die bedingte
Wahrscheinlichkeit für das Eintreffen von Ereignis A unter der Bedingung, dass
B eingetroffen ist, ist W(A|B) = ![]() ;
W(B) > 0
;
W(B) > 0
Die Ereignisse A und B sind genau dann voneinander unabhängig, wenn folgendes gilt:
W(A|B) = W(A) bzw. W(B|A) = W(B)
Beweis: W(A|B) = ![]() =
= ![]() = W(A)
= W(A)
Satz von der totalen Wahrscheinlichkeit
Es seien A1,A2, ,An paarweise disjunkte Ereignisse mit A1+A2+A3++An = S.
Dann gilt für ein beliebiges Ereignis K folgendes:
W(K) = ![]() K
¹ ; K Ì S
K
¹ ; K Ì S
Beweis: W(K) = ![]() K)
K)
Satz von Bayes
(Apostori-Wahrscheinlichkeit, Ereignis ist bereits eingetroffen)
Es seien A1,A2, ,An paarweise disjunkte Ereignisse mit A1+A2+A3++An = S.
Dann gilt für ein beliebiges Ereignis K folgendes:
W(K) = ![]()
W(Ai|K) =
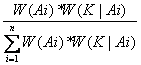
Beweis: W(Ai|K) W(K) = W(K|Ai) W(Ai) = W(Ai K)
W(Ai|K) = ![]()
Diskrete und stetige Zufallsvariablen
Eine ZV, die nur Werte aus einer endlichen oder abzählbaren unendlichen Menge annimmt, heißt diskret. Die Werte sind Sprungstellen, die Wahrscheinlichkeiten Sprunghöhen.
![]() oder
oder ![]()
z.B Poissonsverteilung
Wahrscheinlichten für die Zahlen n, wobei der Erwartungswert = a ist.
W(n)=![]() e-a ; n = 0,1,2,… a>0
e-a ; n = 0,1,2,… a>0
![]() weil
weil ![]() e-a
e-a
Eine ZV ist stetig, wenn eine nicht negative Funktion f existiert, so dass für die Verteilungsfunktion folgendes gilt:
F(x) = ![]() f(t)
heißt dichte Funktion; F(
f(t)
heißt dichte Funktion; F(![]() )
= 1 => F(
)
= 1 => F(![]() )
=
)
= ![]() = 1
= 1
ð Fläche, die über eine ganze reelle Fläche nur 1 ergibt
W(a![]() X
X![]() b) =
F(b) – F(a)
b) =
F(b) – F(a)
![]() -
- ![]()
=![]() +
+ 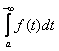 =
= 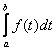
ð wird nie negativ, integral unter der Kurve über der x- Achse muss 1 sein -> dann Dichte
ð Fläche muss betrachtet werden, nicht die Kurve
ð Bsp. Gaußsche Glockenkurve
Unstetigkeits-/ Sprungstelle
![]()
 0 für t<0
0 für t<0
![]()
![]()
![]()
![]() 0 für t > 2
0 für t > 2
![]() =
=
![]()
![]() dt
=
dt
= ![]()
![]()
W(1![]() X
X![]() 1,5)
=
1,5)
= ![]() dt
=
dt
= ![]()
![]() =
= ![]() -
- ![]() =
0,3125
=
0,3125
W(1![]() X
X![]() 1)
=
1)
= ![]() dt
= 0
dt
= 0
Zufallsvariablen & Verteilungsfunktionen
Definition einer Zufallsvariablen
Eine Funktion x, die die Elementarereignisse s hat, injektiv (umkehrbar eindeutig) auf die reelen Zahlen abbildet, heißt Zufallsvariable. Das Urbild (Definitionsbereich) eines reellen Zahlenintervalls I = (-∞;y) ist ein Ereignis.
z.B. Würfel: x (1 fällt) = 1.. x( 6 fällt) = 6
Urbild = x –1 ( -∞; 3,8) = // Ereignis besteht aus 1 – 3
Definition der Verteilungsfunktion
Sei x eine Zufallsvariable (den Ereignissen Zahlen zuordnet), dann ist F(x) mit der Wahrscheinlichkeit das X kleiner ist als x, dann heißt F(x) die Verteilungsfunktion der Zufallsvariablen x
ð sei x ZV, dann ist F(x) = W(X <x)
z.B Würfel: F(3,8) = ½ (1-3 von 6 Fällen)
F(-3) = 0 (gibt es nicht)
F(5)
= ![]() (
( ![]() => Zahlen 1-4 von 6, ohne 5 und 6)
=> Zahlen 1-4 von 6, ohne 5 und 6)
F(29,8) = 1 (alle 1-6)
Zum Verständnis:
F ist nicht monoton fallend: x1> x2 => F(x1) ³ F(x2)
F(-¥
F(+¥
x![]() |R
|R
Mittelwertberechnung allgemein
![]()
E(x) = m = a
E(x) = m = n * p
![]()
Streuung und Standardabweichung
Sei X eine Zufallsvariable, dann heißt E ( [ X-E(X) ]² ) die Streuung (Varianz, Dispersion) von X.
E ( [ X-E(X) ]² ) = D² = ![]() ² =
V²(X) Streuung
² =
V²(X) Streuung
E ( [ X-E(X) ]² ) = E (X)² - [E (X)]²
![]() = D =
= D = ![]() Standardabweichung
Standardabweichung
Beispiel Reparaturwerkstatt:
X1 = 700 W(X1) = 0,5
X2 = 1000 W(X2) = 0,3
X3 = 1100 W(X3) = 0,2
W(X) X X – E(X) [X – E(X)]² E ( [X – E(X)]² )
700 -170 28.900 0,5
1000 130 16.900 + 0,3
1100 230 52.900 + 0,2
= 30.100 = ![]() ²
²
173,5 = ![]()
Ungleichung von Tschebyscheff
![]()
3 - ![]() -Regel: k = 3
-Regel: k = 3 ![]()
Die Wahrscheinlichkeit, dass der Wert
zwischen m-3![]() und m+3
und m+3![]() liegt, ist bei 1-
liegt, ist bei 1- ![]() (~ 90%).
(~ 90%).
Normalverteilung (Gauß-Verteilung)
N(m, ![]() )
)
Dichte der Normalverteilung: f(t) = ![]() e -
e -![]()
Verteilungsfunktion: F(x) = ![]() e -
e -![]() dt
dt
F(2)
= ![]()
Normierte Normalverteilung (Sonderfall)
N(0;1) //Mittelwert
m = 0; Standardabweichung ![]() = 1
= 1
f(t) = ![]() e -
e -![]()
W (x1
< X < x2) = F(x2)
– F(x1) = ![]()
Beispiel:
W(1,13 £ X £ 2,85) = F(2,85) – F(1,13)
= 0,12705
W(-x) = 1 – W(x)
W(-0,5) = 1 – W(0,5)
W(-1 £ X £ 1) = F(1) – F(-1)
= F(1) – (1 – F(1))
= 2 F(1) – 1
= 0,68268
Umrechnung von m und d auf 0 und 1
X sei N(0;1)
Y sei N(m; ![]() ) Y = m +
) Y = m +![]() X
X
X = ![]()
Für x< 0, gilt ![]()
Beispiel:
W(180 £ Y £ 200); Y ist nach N(195;7)
F(200) – F(180)
=
![]() (
(![]() )
-
)
- ![]() (
(![]() )
)
=
![]() (
(![]() )
-
)
- ![]() (
(![]() )
)
=
![]() 0,71
-
0,71
- ![]() - 2,14
- 2,14
=
![]() 0,71
– 1 +
0,71
– 1 + ![]() 2,14
2,14
= 0,76115 – 1 + 0,98382
= 0,74

|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2412
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved