| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
(mettere formula partitore di tensione)
Soluzione dei circuiti in regime sinusoidale
FORMULE UTILI
Passaggio da rappresentazione in f. tempo ![]() a Forma simbolica
(numeri complessi) e vettoriale:
a Forma simbolica
(numeri complessi) e vettoriale:
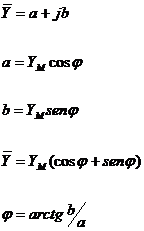
dove:
![]()
Induttore: ![]()
In regime continuo è come cortocircuito
In regime sinusoidale sfasa la corrente che l’
attraversa in ritardo di p/2 rispetto
alla tensione indotta ai propri morsetti (cioè ![]() )
)
reattanza induttiva XL=wL=2pfL
legge Ohm per l’ induttore ![]()
Impedenza di un induttore (è N° immaginario): ![]()
Condensatore: ![]()
In regime continuo è come circuito aperto
In regime sinusoidale sfasa la propria
corrente in anticipo di p/2 rispetto
alla tensione ai propri morsetti: cioè ![]()
reattanza capacitiva ![]()
legge Ohm per il condensatore ![]()
Impedenza di un condensatore (pure N° complesso):
![]()
Espressione generale tensione-corrente bipolo lineare passivo qualunque in regime armonico
![]()
Impedenza Z: N° complesso, parte reale costante, parte immaginaria variabile con la f
Modulo impedenza ![]()
Fase impedenza ![]() cioè:
cioè: ![]()
Quoziente numeri complessi:
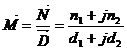
Modulo: 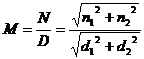
Fase: ![]()
N.B. Fase impedenza = sfasamento tra TENSIONE e corrente:
![]()
N.B. Proprietà unità immaginaria:
![]() cioè
cioè ![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1263
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved