| CATEGORII DOCUMENTE |
| Comunicare | Marketing | Protectia muncii | Resurse umane |
Modelarea fenomenelor de piata
Cunoasterea cerintelor pietei si anticiparea acestora constituie una din premisele care stau la baza intocmirii programului de productie intr-o intreprindere, prospectarea pietei reprezentand un proces complex care se refera atat la aspecte cantitative cat si calitative. In cercetarile specifice de prospectare a pietei se folosesc, atat date statistice privind evolutia cererii si ofertei de produse pe diferitele piete, cat si informatii culese direct de pe piata, din confruntarea cererii si ofertei.
In cadrul acestor modele vom analiza raportul cerere-pret si raportul cerere-venit.
1.1 Modelarea evolutiei cererii pe piata in functie de
raportul cerere-pret
Teoria cantitativa a cererii porneste de la urmatoarele ipoteze:
(a) in cazul unui venit constant, cererea pentru o anumita marfa scade odata cu cresterea pretului si invers. Aceasta ipoteza permite formularea unor modele numerice cu care sa se previzioneze cresterea sau scaderea cererii, in cazul reducerii sau cresterii pretului, intr-o proportie definita. Sensibilitatea cererii la modificarile de pret, arata cu cat la suta se modifica, in sens invers, cererea unui bun daca pretul sau se modifica cu 1%. Elasticitatea cererii functie de pret se determina cu ajutorul relatiei 1. de mai jos.
Ec/p = ( DC / C0 ) / ( DP / P0 ) (1.)
unde:
DC si DP reprezinta sporul cererii respectiv al pretului in doua perioade de referinta
(b) in cazul in care venitul este variabil, cererea unui bun creste odata cu cresterea venitului si scade cu cresterea pretului. Daca presupunem, pentru fiecare nivel al venitului, existenta unei functii ƒv a cererii, atunci cererea in functie de venit poate fi reprezentata cu ajutorul relatiei nr. 2.
Ci = ƒv ( Pj ) (2.)
Modificarile posibile ale cererii vor putea fi reprezentate prin mai multe curbe ale cererii succesive, in functie de nivelul pretului.
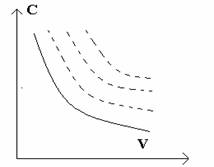
Figura nr. 1. - Raportul cerere - pret
1.2 Modelarea evolutiei cererii pe piata in functie de
raportul cerere-venit
Daca pretul este mentinut constant, cererea pentru un anumit bun poate fi descrisa ca o functie a venitului exprimata cu ajutorul relatiei nr. 3.
Coeficientul de elasticitate a cererii in functie de venit arata cresterea procentuala a cererii, atunci cand venitul creste cu 1%.
Ec/v = DV / V0
Modificarile preturilor, in doua perioade de timp, determina deplasarea curbei cererii. In literatura de specialitate curbele care exprima dependenta dintre cerere si venit sunt cunoscute sub denumirea de curbe Engel. Dependenta cererii de venit poate fi exprimata, in principal, prin urmatoarele tipuri de functii:
(a) in cazul bunurilor de stricta necesitate, dependenta cererii in functie de venit (C1), arata ca pe masura cresterii veniturilor, cererea pentru aceste bunuri creste intr-o proportie mai slaba, tinzand sa se plafoneze. Dependenta dintre venit si cerere, in acest caz, poate fi exprimata sub forma unei curbe exponentiale cu plafonare. Curba cererii, folosind relatia nr.
C1 = ( m1 * b ) / ( V + n1 ) ()
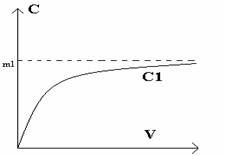
Figura nr. 2. - Raportul cerere - venit in cazul bunurilor de stricta necesitate
(b) in cazul bunurilor de consum curent, curba cererii (C2) prezinta aproximativ aceeasi dependenta cerere / venit, ca si in cazul C1, deoarece are un prag de saturatie (la nivelul lui m2), ceea ce inseamna ca la cresteri din ce in ce mai mari ale veniturilor curba cererii tinde catre plafonul m2.
C2 = [ m2 ( V - P2 ) ] / ( V + n2 ) (5.)
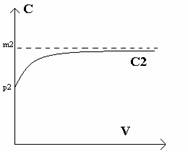
Figura nr. 3. - Raportul cerere - pret in cazul bunurilor de consum curent
(c) in cazul bunurilor de lux, cererea acestor produse, creste continuu pe masura cresterii veniturilor. Curba cererii (C3) se prezinta ca o asimptota oblica spre +¥ la ramura Ox.
C3 = [ m3 * V ( V - P3 ) ] / ( V + n3 ) (6.)
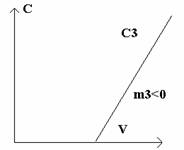
Figura nr. - Raportul cerere - pret in cazul bunurilor de lux
(d) in cazul bunurilor, care pentru un anumit nivel al veniturilor sunt scoase din uz, cererea prezinta la inceput o crestere, atinge un maxim, dupa care incepe sa scada catre zero, ceea ce inseamna ca pentru venituri din ce in ce mai mari, nu exista cerere pentru astfel de produse.
2 Modelarea structurii ofertei intreprinderilor pe piata
2.1 Indicatorii ofertei de marfuri
Oferta de marfuri trebuie tratata in profil static si dinamic, pentru a putea fi surprinsa atat la un moment dat cat si in miscare, cu implicatiile ce le atrage prezenta sa asupra procesului economic in complexitatea lui. Cresterea cantitativa, ridicarea calitativa, diversificarea sortimentala, innoirea produselor in timp, reprezinta principalii parametri ce caracterizeaza dinamica ofertei de marfuri. Fiecarui produs din masa globala a ofertei i se poate individualiza relativ usor varsta, pornind de la momentul primei sale aparitii pe piata. La un anumit moment dat (analizata static), oferta cuprinde produse cu varste foarte diferite, ea avand varsta medie ( simpla sau ponderata ) a varstei produselor care o compun.
Viata produselor pe piata cunoaste etapele de: lansare, crestere, maturitate si declin. Curba vanzarilor arata caracterul progresiv al penetratiei produsului in consum, stabilitatea relativa din perioada de maturitate, precum si concurenta pe care produsele noi o fac celor vechi, sfarsind prin eliminarea acestora de pe piata.
2.2 Modelarea evolutiei ponderii pe piata a unor produse
concurentiale (lanturile Markov)
2.2.1. Definitie
Procesele Markov sunt procese stocastice care modeleaza situatiile in care tranzitia intre diverse stari nu este determinista ci probabilistica, fiind caracterizata prin aceea ca probabilitatea de tranzitie la o stare succesiva, depinde exclusiv de starea actuala.
Fie doi jucatori A si B care decid sa joace cu o moneda, probabilitatea sa iasa cap (p) si pajura (1-p). Cu (a) si (b) vom nota capitalurile initiale a celor doi jucatori A si B.
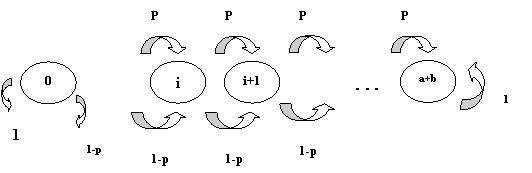 Dorind sa modelam procesul
de variatie a capitalurilor intre cei doi jucatori, decidem capitalul lui A, poate sa varieze intre urmatoarele limite:
0 in cazul in care pierde si (a+b)
cazul in care castiga. Situatia poate fi reprezentata ca in figura 5.
Dorind sa modelam procesul
de variatie a capitalurilor intre cei doi jucatori, decidem capitalul lui A, poate sa varieze intre urmatoarele limite:
0 in cazul in care pierde si (a+b)
cazul in care castiga. Situatia poate fi reprezentata ca in figura 5.
Capitalul jucatorului A variaza intre valoarea initiala zero si (a+b), crescand succesiv in pasi de unu si cu probabilitatea (p) sau scazand cu probabilitatea q=(1-p). Probabilitatea de crestere sau descrestere a capitalului nu este dependenta de numarul de trageri (n).
Orice proces Markov se caracterizeaza prin urmatoarele trasaturi-caracteristici sau proprietati:
lanturile sunt treceri intre diverse stadii si se realizeaza in mod probabilistic;
probabilitatea de tranzitie nu depinde de numarul de tranzitii efectuate;
probabilitatile de trecere sau tranzitie depind doar de starea actuala sau prezenta (proprietatea memoryless, sau de lipsa a memoriei).
Orice lant Markov este definit complet prin matricea sa stocastica (P) si distributia initiala (ai). Considerand un ansamblu de rezultate posibile E1, E2, ., En in numar finit sau infinit, iar fiecarui rezultat ii asociem o probabilitate de manifestare (Pk), probabilitatea unei succesiuni de rezultate se defineste printr-o proprietate multiplicativa de forma celei prezentate in relatia nr. 7.
P ( Ej0, Ej1, ., Ejn ) = Pj0* Pj1* .*Pjn
In teoria lanturilor Markov se considera ca rezultatul oricaror incercari depinde de rezultatul incercarii care o precede direct si numai de acesta. Fiecarui rezultat Ejk i se asociaza o probabilitate Pjk, adica daca se realizeaza Ej, probabilitatea de realizare a lui Ek este Pjk. Probabilitatea rezultatului Ej al incercarii initiale este aj. Probabilitatea conditionata este probabilitatea de trecere de la starea Ej la starea (rezultatul) Ek. Probabilitatile de trecere sunt reprezentate sub forma unor matrice patratice cu toate elementele nenegative si cu proprietatea ca suma elementelor unei aceleiasi linii este egala cu 1.
2.2.2. Metoda de lucru
Pe piata televizoarelor color sunt prezente trei produse concurentiale: C1; C2 si C3. Un sondaj de piata, care avea drept scop testarea preferintelor consumatorilor cu privire la cele 3 marci, a scos in evidenta urmatoarele:
coeficientii de fidelitate ai consumatorilor fata de cele 3 marci de televizoare s-au determinat plecand de la urmatoarele atribute: calitatea imaginii; calitatea sunetului; design; pret; ambalaj;
Rezultatele obtinute se pot sintetiza in urmatorii coeficienti de fidelitate: 55% din cumparatori raman fideli lui C1; 65% din cumparatori raman fideli lui C2; 75% din cumparatori raman fideli lui C3;
Ceilalti cumparatori parasesc produsul si se orienteaza spre celelalte dupa cum urmeaza:
Tabelul nr. 1.- Situatia cotelor de piata

Considerand constante probabilitatile de tranzitie, se analizeaza evolutia ponderii pe piata a celor trei produse pentru un semestru. Se stabilesc politicile manageriale pentru fiecare produs in parte, la firma care-l produce.
La stabilirea modului in care se presupune sa evolueze ponderea pe piata a unor produse concurentiale, se poate aplica metoda "Lanturile Markov".
Pasul 1 se construieste matricea probabilitatilor de tranzitie (P), in functie de coeficientul de fidelitate si de reorientarile cumparatorilor in doua perioade succesive. Probabilitatile de tranzitie sunt reprezentate sub forma unor matrice patratice, cu toate elementele nenegative si cu proprietatea ca suma elementelor unei aceleiasi linii trebuie sa fie egala cu 1;
Pasul 2 - se scrie distributia initiala sub forma unui vector linie, cu elemente formate din ponderile pe piata ale produselor la momentul zero;
Pasul 3 - se determina ponderea pe piata a produselor dupa prima perioada. Pentru a obtine ponderea pe piata a produselor pentru perioada urmatoare, rezultatul anterior va fi inmultit cu matricea probabilitatilor de tranzitie de la o stare la alta.
1. Se construieste matricea probabilitatilor de tranzitie:

2. Se construieste vectorul linie cu ponderile de piata a celor trei produse la momentul initial:
![]()
3. Se determina cotele de piata ale celor trei produse dupa prima luna:

Se determina cotele de piata ale celor trei produse dupa a doua luna:
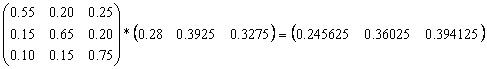
5. Se determina cotele de piata ale celor trei produse dupa a treia luna:
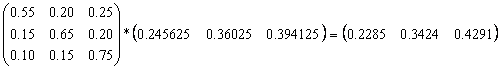
6. Se determina cotele de piata ale celor trei produse dupa a patra luna:
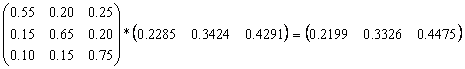
7. Se determina cotele de piata ale celor trei produse dupa a cincea luna:

8. Se determina cotele de piata ale celor trei produse dupa a sasea luna:
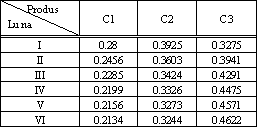
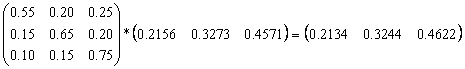 9. Centralizand datele, vom
obtine tabelul nr. 3. de mai jos.
9. Centralizand datele, vom
obtine tabelul nr. 3. de mai jos.
10. Grafic evolutia ponderii produselor pe piata va arata ca in figura nr. 6.
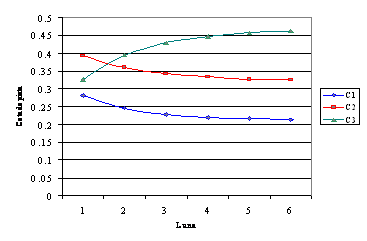
Figura nr. 6.- Evolutia cotelor de piata a produselor analizate
Atat din graficul de mai sus cat si din datele cuprinse in situatia centralizata a ponderii pe piata a celor trei produse putem trage urmatoarele concluzii:
- produsul C1 si produsul C2 se afla in faza de declin. Se observa ca produsul C1 are initial o cota de piata de 35%, pentru ca in final sa ajunga la o cota de piata de aproximativ 21%. Similar, cota de piata a produsului C2 inregistreaza o scadere de la 45% la aproximativ 32%.
Declinul este ultima faza din ciclul de viata a produsului. Aceasta etapa este caracterizata de reducerea volumului vanzarilor, fenomen asociat cu reducerea cotei de piata pe care o detine produsul, datorita nu atat consumului specific, cat mai ales datorita renuntarii din clientela in favoarea unor produse noi.
Cand se produc aceste fenomene, vanzatorii considera ca articolele din linia de productie care nu aduc profit trebuie eliminate. In aceste conditii, vanzatorii pot reduce eforturile de promovare, pot elimina distribuitorii marginali iar in final, sa planifice scoaterea din fabricatie a produsului.
- produsul C3 se afla in faza de crestere. Cota de piata a produsului C3 creste de la 20% la aproximativ 46%. In etapa de crestere, produsul capata cale libera prin acceptarea sa de catre consumatori, cunoaste o ascensiune rapida a vanzarilor, o reducere a cheltuielilor si o crestere a beneficiilor.
Strategiile de crestere au in vedere:
imbunatatirea calitatii produselor si adaugarea de noi modele sau caracteristici;
penetrarea pe noi segmente de piata;
cucerirea unor noi spatii pentru produsul propriu in canalele de distributie;
folosirea unei parti din publicitate pentru realizarea obiectivului ce urmareste convingerea cumparatorilor in a efectua actul cumpararii;
diminuarea sensibila a preturilor in scopul atragerii unor noi contingente de consumatori sensibili la aceste reduceri. Pretul promotional agresiv, ce include reduceri de preturi, este tipic acestei etape.
3 Metode si modele de prognozare a vanzarii produselor
3.1 Modelul de livrare a unor produse conform unui
spectru constant (metoda vectorilor spectrali)
Pe baza valorii comenzilor emise se intocmeste matricea C(t-r1;t+r2), componentele acestei matrice fiind reprezentate de comenzile valorice emise in trecut. (t - r1) reprezinta comanda mai veche, iar (t + r2 ) comenzile viitoare. Vanzarile de marfuri pentru perioada (t , t+r2) se determina conform relatiei nr. 8.
C ( t ; t + r2 ) = C ( t - r1 ; t + r2 ) * Vj
Pentru determinarea previziunii vanzarilor pentru o perioada de cateva luni se va folosi metoda vectorilor spectrali. Metoda "vectorilor spectrali" se bazeaza pe descompunerea spectrului succesiunii in timp a unei comenzi, conform graficului de livrare, pe baza unor date din trecut privind evolutia sau structura acestora.
2.2.2 Metoda de lucru
Pentru determinarea previziunii vanzarilor pentru o perioada de cateva luni se va folosi metoda vectorilor spectrali. Metoda "vectorilor spectrali" se bazeaza pe descompunerea spectrului succesiunii in timp a unei comenzi, conform graficului de livrare, pe baza unor date din trecut privind evolutia sau structura acestora.
1. Se construieste matricea extinsa a comenzilor ce formeaza in primul pas astfel:
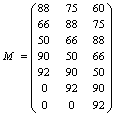
2. Se construieste vectorul spectral:
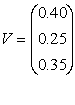
3. Se inmulteste matricea extinsa a comenzilor cu vectorul
spectral si se determina valoarea livrarilor de marfuri in luni succesive
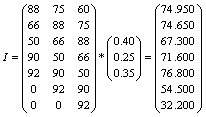
Toate comenzile primite vor fi lichidate in luna (t+7), adica luna februarie. Valoarea totala a comenzilor care s-au emis in perioada (t; t+6) va fi de 452 mii t. (7950 + 7650 + 67.300 + 71.600 + 76.800 + 5500 + 32.200) cu urmatoarea esalonare lunara:
7950 mii t in luna august;
7650 mii t in luna septembrie;
67.600 mii t in luna octombrie;
71.600 mii t in luna noiembrie;
76.800 mii t in luna decembrie;
5500 mii t in luna ianuarie;
32.200 mii t in luna februarie.
In cantitatea totala comandata de 452 mii t sunt cuprinse integral lunile august-decembrie si cote parti din comenzile emise in lunile precedente.
3.2 Metoda ajustarii exponentiale a lui Brown
3.2.1 Definitie
Ajustarea exponentiala reprezinta o suma ponderata a tuturor datelor din trecut ale unei serii dinamice cu ponderea cea mai mare, plasata asupra celei mai recente informatii. Datele sunt nivelate cu ajutorul unei constante de nivelare aI
Ideea de baza a metodei consta in proiectarea previziunii, proportional cu abaterea constanta intre previziunile anterioare si realizarea lor, fiecare abatere fiind ponderata geometric, descrescand pe masura ce se indeparteaza de prezent (diminuarea progresiva a influentei informatiilor mai indepartate).
In aceste conditii, fiecarei valori din seria cronologica a unui fenomen i se ataseaza cate un coeficient de ponderare diferentiat, astfel incat sa confere evenimentelor, incepand cu cele mai recente, o importanta care scade exponential odata cu vechimea, astfel incat, de la un moment dat, mergand spre trecut, evenimentele sa nu mai aiba nici o importanta asupra previziunii.
Metoda ajustarii exponentiale presupune parcurgerea urmatoarelor etape:
(a) se stabileste apartenenta fenomenelor la unul din cele 4 tipuri de evolutii de mai jos:
evolutia liniara orizontala caracterizata de medie;
evolutia cu tendinta liniara caracterizata de medie si panta dreptei;
evolutia orizontala cu sezonalitate caracterizata de medie si factor de sezonalitate;
evolutia cu tendinta sezoniera caracterizata de medie si factor de sezonalitate;
(b) se descompune fenomenul in componentele sale caracteristice, calculandu-se marimea lor;
(c) se recompune fenomenul din marimile caracteristice, pentru o perioada viitoare realizand astfel previziunea propriu-zisa.
Pentru a calcula previziunea pentru o anumita perioada si un anumit fenomen sunt necesare trei tipuri de date:
vanzarile realizate in ultima perioada a seriei de date ( St );
previziunile realizate pentru vanzarile din ultima perioada a seriei de date ( Rt-1 );
valoarea factorului ponderator de nivelare ( a
Pe baza acestor date expresia previziunii vanzarilor facute la sfarsitul perioadei "t" pentru perioada urmatoare "t+1" poate fi scrisa conform relatiei nr. 9.
Rt = a * St + ( 1 - a ) Rt-1 (9.)
Aceasta formula ne arata ca putem previziona, plecand de la previziunea pentru ultimele desfaceri ale seriei vanzarilor lunare efective, corectand-o cu o fractiune de eroare (diferenta dintre vanzarile realizate in ultima perioada si previziunile de vanzari facute in aceasta perioada).
Factorul Rt cuprinde si sintetizeaza toate previziunile din trecut, lucru foarte important in efectuarea calculelor numerice.
Pornind de la valorile pe care le poate lua a, in practica ne intalnim cu urmatoarele situatii:
daca a=1, atunci valoarea previziunii este egala cu valoarea previziunii efectuate ( Rt = St );
daca a 0, influenta rezultatelor vanzarilor recente asupra previziunii va fi mai mica ( previziunile de la o perioada la alta vor tinde sa fie constante ) Rt = Rt-1 + St
daca a 1, influenta vanzarilor din ultimele perioade, asupra previziunii pentru perioada urmatoare va fi mare.
Rt = St + Rt-1¯ (10)
3.2.2 Metoda de lucru
Firma OLFIL din Oltenita, comercializeaza fire si fibre din bumbac si tip bumbac consumatorilor industriali de pe piata interna a Romaniei. Compartimentul de vanzare inregistreaza, evidentiaza si analizeaza datele obtinute (cantitative si valorice) din vanzarea produselor firmei. Volumul vanzarilor cantitativ inregistrate de catre compartimentul de desfacere si comercializare sunt prezentate in tabelul urmator:
|
Luna calendaristica |
Vanzari cantitative (t) |
|
Ianuarie 2002 | |
|
Februarie 2002 | |
|
Martie 2002 | |
|
Aprilie 2002 | |
|
Mai 2002 | |
|
Iunie 2002 | |
|
Iulie 2002 | |
|
August 2002 |
Lunar se efectueaza prognoze asupra vanzarilor lunii viitoare, pentru dimensionarea stocurilor si orientarea cheltuielilor de transport si distributie.
Conducerea firmei este interesata in estimarea volumului vanzarilor pentru luna septembrie 2002, cunoscand ca previziunea initiala pentru luna ianuarie 2002 a fost de 72 unitati monetare. Din analiza datelor statistice anterioare se estimeaza ca valoarea coeficientului de nivelare este
a) se identifica momentele impreuna cu vanzarile cantitative specifice fiecarui moment in parte, astfel:
|
Momentul t |
Vanzari cantitative Yt |
b) se calculeaza prognozele corespunzatoare momentelor t; t+1 pentru un
F2= Y1+(1- )F1 = 0.3*88 + 0.7*72 = 26.4 +50.4 = 76.8;
F3 = Y2+(1- )F2 = 0.3*93 + 0.7*76.8 = 27.9 +53.76 = 81.66;
F 4= Y3+(1- )F3 = 0.3*85 + 0.7*81.66 = 26.4 + 57.16 = 82.6;
Rezultatele care se obtin in urma calculelor, pot fi sintetizate ca in tabelul de mai jos:
|
Perioada |
Luna |
a |
1-a |
Vanzari |
Prognoze |
|
to | |||||
|
to | |||||
|
to | |||||
|
to | |||||
|
to | |||||
|
to | |||||
|
to | |||||
|
to | |||||
|
t1 |
xx |
xx |
xx |
Reprezentarea grafica a evolutiei vanzarilor efective si a previziunilor, poate fi facuta, ca mai jos:
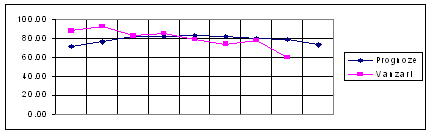
c) se calculeaza prognozele corespunzatoare
momentelor t; t+1 pentru un
= 0.8. Rezultatele care se obtin, dupa aceeasi metodologie de calcul, pot fi
sintetizate ca in tabelul de mai jos:
|
Perioada |
Luna |
a |
1-a |
Vanzari |
Prognoze |
|
to |
| ||||
|
to | |||||
|
to | |||||
|
to | |||||
|
to | |||||
|
to | |||||
|
to | |||||
|
to | |||||
|
t1 |
xx |
xx |
xx |
d) se calculeaza prognozele corespunzatoare momentelor t; t+1 pentru un = 0.95. Rezultatele care se obtin, dupa aceeasi metodologie de calcul, pot fi sintetizate ca in tabelul de mai jos:
|
Perioada |
Luna |
a |
1-a |
Vanzari |
Prognoze |
|
to | |||||
|
to | |||||
|
to | |||||
|
to | |||||
|
to | |||||
|
to | |||||
|
to | |||||
|
to | |||||
|
t1 |
xx |
xx |
xx |
e) se calculeaza prognozele corespunzatoare momentelor t; t+1 pentru un = 0.15. Rezultatele care se obtin, dupa aceeasi metodologie de calcul, pot fi sintetizate ca in tabelul de mai jos
|
Perioada |
Luna |
a |
1-a |
Vanzari S |
Prognoze R |
|
to | |||||
|
to | |||||
|
to | |||||
|
to | |||||
|
to | |||||
|
to | |||||
|
to | |||||
|
to | |||||
|
t1 |
xx |
xx |
xx |
Din exemplele de mai sus se constata ca, valori a lui apropiate de 1 fac ca valoarea previziunii sa se apropie foarte mult de valoarea vanzarilor reale din ultima perioada, din care se are la dispozitie inregistrari statistice. Daca se apropie de zero, valoarea previziunii se indeparteaza mult de valoarea reala a ultimelor vanzari.
|
Luna |
Vanzari efective |
Previziuni a=0.15 |
Previziuni a=0.3 |
Previziuni a=0.8 |
Previziuni a=0.95 |
|
xx |
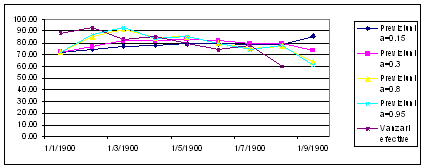
4 Extrapolarea fenomenologica
Activitatile comerciale, in general, nu se desfasoara pe baza de comenzi ferme. Cumparatorii nu comanda dinainte o marfa pe care apoi sa o cumpere in mod sigur. De aceea cunoasterea nivelului cererii de marfuri se face pe baza unor prognoze.
O tehnica de prognoza foarte des utilizata este extrapolarea fenomenologica. Aceasta presupune cunoasterea tipului de evolutie a fenomenului studiat, exprimat sub forma unei functii matematice, numita functie de extrapolare.
Proprietatile functiilor matematice, cu ajutorul carora se extrapoleaza evolutia proceselor economice trebuie sa corespunda particularitatilor acestora.
Problema centrala a acestui tip de prognoza este aceea a stabilirii tipului functiei de extrapolare, adica a alegerii din multimea functiilor matematice cunoscute a uneia, care sa aiba un grad mare de fidelitate cu fenomenul economic studiat.
Principalele functii matematice ce pot fi utilizate in prognozarea fenomenelor economice sunt:
a) curba liniara cu plafonare;
b) curba exponentiala;
c) curba variatiei sigmoide;
d) curba functiei logice;
e) curba gaussiana.
Aceste functii descriu legaturile care s-au format in perioada trecuta intre doua sau mai multe marimi economice considerate ca variabile matematice, si permit aprecierea nivelelor probabile, in perspectiva, pornind de la ideea mentinerii in continuare a acestor legaturi.
Extrapolarea seriilor dinamice, ca metoda de prognoza, prezinta si o serie de dezavantaje, si in primul rand pe acela ca nu poate sa tina seama de schimbarile care pot modifica in viitor, legatura dintre marimile economice si aparitia de noi factori de influenta.
Cu toate acestea, extrapolarea fenomenologica are o larga utilizare, deoarece permite aprecierea evolutiilor viitoare a unui proces economic, metoda care insa trebuie utilizata si corelata cu rezultatele obtinute cu ajutorul altor metode de previziune.
Utilizarea functiilor matematice capata un sens economic numai in conditiile in care, marimile luate in considerare, prezinta o interdependenta reala.
Complexitatea relatiilor economice face necesara utilizarea functiilor de corelatie cu mai multe variabile independente si mai putin a corelatiei simple.
Obtinerea rezultatelor satisfacatoare depinde in mod esential, de alegerea acelor functii matematice care descriu cel mai bine evolutia procesului economic studiat.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3923
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved