Modelarea matematica a aeronavelor

Generalitati

Fara modelarea matematica a evolutiilor aeronautice, a sistemelor si a elementelor constitutive specifice unei aeronave nu se poate concepe un sistem de antrenament sau un simulator de zbor.

Dificultatea modelarii matematice a fenomenelor specifice zborului aeronavelor este mare, deoarece complexitatea fenomenelor este deosebita, implicind zone de granita ale stiintelor si fenomene aerodinamice complexe si tranzitorii. Reprezentarea matematica a legilor care guverneaza evolutiile unei aeronave este definitorie pentru nivelul de fidelitate al simulatoarelor de zbor.

Pe linga performantele care cresc exponential in timp ale echipamentului de calcul, pe linga gradul de acuratete al imaginii proiectate pe diferite tipuri de ecrane si cu diverse tipuri de proiectare, calitatea actului de simulare este determinata de acuratetea modelarii aeronavei.

Deci o problema majora a simulatoarelor este si va fi gradul de modelare matematica care va determina veridicitatea situatiei din simulator fata de situatia reala.

In capitolele precedente s-au prezentat cateva concepte generale despre modul de modelare, gradul de adecvanta, etc. si modul cum se poate realiza un model.

Esential este ca pilotul care se afla in simulator sa "simta" ca acesta raspunde la fel ca avionul real; ca se pot realiza anumite misiuni care presupun zbor la o anumita inaltime, cu o anumita viteza si ca instruirea sa este corecta si adecvata cu situatia reala.

In fata celor ce elaboreaza modele matematice se pun de obicei 3 mari probleme care pot fi rezolvate fiecare cu o anumita aproximatie:

1.modelarea matematica, adica problema descrierii cu ecuatii, tabele, grafice a comportamentului aeronavei in toate regimurile de functionare si cu toate sistemele aferente;

2.definirea si corelarea tuturor parametrilor care influenteaza antrenamentul pe simulator;

3.problema timpului real adica a realizarii unor sisteme de calcul capabile sa asigure functionarea simulatorului in timp real deoarece este esential ca bucla "om-simulator" sa functioneze la fel ca in aeronava si la aceeasi scara de timp.

1. MODELAREA MATEMATICA A AVIONULUI

Pilotul care se antreneaza pe simulator trebuie sa poata efectua totalitatea operatiilor si manevrelor la fel ca in cazul real, gradul general de veridicitate si a manevrelor ce se pot studia pe simulator fiind clar definit in cazul clasificarii performantelor simulatoarelor. Esential este ca actiunea pilotului din cabina simulatorului asupra comenzilor principale si secundare (in conformitate cu misiunea si tipul aeronavei) sa determine reactii corespunzatoare prin aparatura de bord, sistemul de imagine, sistemul sonor, de miscare etc. Modelarea matematica presupune ca toate sistemele de ecuatii asociate miscarii aeronavei, pentru toate domeniile de viteza, altitudine si atitudine se pot rezolva, si ca s-a efectuat modelarea tuturor sistemelor de la bordul aeronavei.

Aceasta modelare trebuie sa se faca cu diferite precizii determinate de influenta fiecarui factor din model asupra gradului de simulare.

De exemplu: modificarea parametrilor aerodinamici este esentiala din punct de vedere al portantei si din punct de vedere al atitudinii aeronavei in cazul scoaterii trenului de aterizare sau a actionarii unor suprafete ca spoilere, frane aerodinamice etc. si este neglijabila, (la inceput) in cazul unei pierderi de presiune in instalatia hidraulica.

In esenta, putem considera ca modelarea matematica presupune rezolvarea numerica in timp real a tuturor sistemelor de ecuatii diferentiale sau algebrice ce descriu matematic modul de raspuns la comenzi a sistemlor avionului inclusiv comportarea dinamica in diverse regimuri de zbor.

Modelele matematice a unor sisteme pot fi mult reduse fara a afecta calitatea simularii, o serie de sisteme se pot modela matematic mult simplificat, esential fiind ca efectul lor perceput de pilot sa fie corect.

De exemplu nu are rost sa se modeleze pina la nivel de componenta electronica sau releu sistem electric al aeronavei deoarece din punct de vedere a pilotului nu este sesizata decit functionarea lui corecta sau nu.

O mare dificultate este faptul ca evolutiile aeronavei nu pot fi standardizate, asa cum se considera in calculele tipice sau in manualele de zbor, trebuie ca aeronava sa raspunda la comenzi ca in cazul real si la evolutii neasteptate deoarece simulatorul este un echipament real in care pilotii gresesc, manevreaza comenzile nu neaparat in ordinea data in manual si se antreneaza pentru cazurile de avarie cind o serie de sisteme nu functioneaza corespunzator.

2. DEFINIREA SI CORELAREA PARAMETRILOR CARE INFLUENTEAZA ANTRENAMENTUL PE SIMULATOR

In faza de definire a unui simulator, a gradului sau de adecvanta, a domeniilor de zbor pentru care este utilizat constructorul de simulator trebuie:

-sa determine in cadrul modelului de ce marimi si parametri din cadrul aeronavei are nevoie,

-sa elimine parametri care nu aduc date importante,

-sa determine scala de variatie pentru cei alesi

-sa aleaga modul cel mai adecvat de calcul.

Analizind apoi modul de calcul si conditiile initiale se considera pentru intregul simulator domenii de eroare si zone in care acuratetea trebuie sa fie deosebita. Trebuie sa se aibe in vedere si gradul foarte mare al complexitatii unei aeronave in care prin gradul sau de autonomie concureaza domenii din ce in ce mai numeroase .

Daca la inceput datorita calitatii slabe a echipamentelor de calcul analogice se cauta sa se minimizeze numarul de parametri, iar erorile in calcularea lor erau mari, in prezent datorita dezvoltarii fantastice a puterii de calcul se pot trata un numar mare de parametri, se pot memora tabele de variatii, se pot considera diverse sisteme de referinta si totul se calculeaza cu o precizia dorita.

Este important ca pe linga aceste metode sa se actioneze si criteriul comercial al celui care poate sa discearna intre un sistem cu o precizie suficienta si un sistem foarte precis, dar care se ridica la un pret exorbitant.

3. PROBLEMA TIMPULUI REAL, O PROBLEMA DE FOND A SIMULATOARELOR

Incepind de la primele simulatoare utilizate la pregatirea pilotilor de bombardiere in al II razboi mondial, constructorii de simulatoare s-au luptat cu timpul, deoarece este cel mai grav lucru sa-l faci pe pilot sa execute o anumita manevra mai incet decit este necesar in realitate.

Miscarile laterale de tip tonoou sau rasturnarile in care portanta se modifica radical in fractiuni de secunda ridica si in prezent probleme deoarece sistemul de calcul trebuie sa raspunda in timp real.

Sistemele de calcul analogice au asigurat acest deziderat de timp real, dar erau greoaie, se deteriorau in timp, aveau derive mari termice si erau complicat de exploatat. Aparitia sistemelor numerice a condus la un grad de complexitate marit, la inceput (datorita dificultatii de a roti matrici, a calcularii ecuatii difentiale etc.), dar in prezent prin dezvoltarea capacitatilor de memorie si de calcul s-au atins performante capabile sa rezolve ecuatiile diferentiale in timp corespunzator.

De asemenea, sistemele de vizualizare sunt concepute sa raspunda corect pentru a genera in timp real imagini corespunzatoare. In general, datele sunt furnizate in sistem intre 20 - 60 de iteratii pe secunda, functie de aeronava si tipul simulatorului.

Analiza sistemelor. Clasificarea modelelor

Pentru a intelege modul de conceptie a unui simulator de zbor pentru aeronava este necesara utilizarea unei discipline de granita denumita analiza sistemelor.

Ea poate fi considerata ca fiind o sinteza a trei domenii din automatica :

1. - teoria identificarii

2. - teoria reglarii automate pentru sisteme

3. - programe de calcul specifice modelarii.

Un model este o reprezentare matematica a unui proces, iar aceasta reprezentare se face cu ajutorul unor ecuatii care descriu si caracterizeaza starile si marimile caracteristice acestui proces. Calitatea unui model este data de gradul de matematizare si de fidelitatea descrierii parametrice si cauzale a tuturor proceselor specifice sistemului sau fenomenului modelat.

Necesitatea acestei discipline-analiza de sisteme a provenit din faptul ca peste o anumita complexitate a unei aeronave, instalatii,proces etc. este dificil sa se modeleze (clasic) pe baza unor ecuatii generale, (fenomenele fiind in interactiune), iar numarul variabilelor este deosebit de mare.

Simularea care in cazul analizat este scopul in sine, poate fi folosita si indirect in cercetarea aeronautica pentru crearea unui model al instalatiei pe calculator.

Problema cheie este ca in cazul aeronavei trebuiesc definite prioritati in programul de calcul si ierarhii astfel incat toata modelarea sa se produca in timp real.

Este clar ca un simulator de zbor nu poate reproduce identic un fenomen atat de complicat cum este de pilda totalitatea factorilot si stariilor de pe o aeronava in timpul unor evolutii din zborul acrobatic, dar asa cum s-a aratat in capitolele anterioare este foarte important ca insusirea tehnicilor de pilotaj sa fie corecta, sa nu se formeze deprinderi false si ca evolutiile aeronavei simulate sa fie reproduse cu un grad cit mai ridicat de fidelitate.

Termenul "model" este folosit din ce in ce mai mult, dar esential este ca el sa cuprinda o descriere matematica valabila, sa aibe un grad de personalizare bine determinat pentru sistemul studiat.

Construirea si elaborarea de modele matematice este partea cea mai importanta a analizei de sisteme, deoarece de calitatea modelului depinde calitatea finala a sistemului de instruire, gradul de adecvanta al echipamentului simulat.

In general modelele pot fi de doua tipuri :

a.      -modele cu continuitate =varioabilele sunt continuui ca variatie in timp si spatiu,

b.      -modele discrete=variabilele variaza discontinuu

Scopul unui model este sa formuleze o descriere cit mai veridica a mecanismului fenomenului in termeni cantitativi,fiecare model continind aproximatii si idealizari inevitabile.

In formularea modelelor continue exista trei cai de a aproxima legile care conduc la explicitarea ecuatilor :

1.Procedura clasica = se bazeaza pe formularea si aplicarea in conditiile date ale legilor fizice de conservare, universal valabile(ex: legea conservarii masei, a momentului si a energiei.

2.Procedura ipotetica = nu se cunosc legile dupa care functioneaza aplicatia, dar prin similitudini aplicam modele cunoscute.

3.Procedura prin identificare=cazul in care nu se cunoaste deloc procesul si se aplica analize ca in cazul unei cutii negre, adica identificam variatia marimilor de iesire functie de anumite tipuri de marimi aplicate la intrare.

Etapele in procedura de modelare sunt urmatoarele:

Modelele ce se utilzeaza in simulare sunt:

Modele fara comanda = modelele descriu procese cu ajutorul unor ecuatii diferentiale sau cu diferente finite care nu contin parametri sau functii de alte variabile. Modelele sunt de obicei stohastice si contin variabile si functii aleatorii :

= f(x, t, x

x- vector aleatoriu dat de o lege de probabilitate cunoscuta

Obs. : Modele tipice pentru procesele din natura: zone ce sunt caracterizate de distributii cunoscute, (ex: variatia gravitatiei, a turbulentei)

2. Modele utilizabile pentru optimizarea unor anumite sisteme

Modelele sunt descrise de ecuatii de tipul :

= f(x, t, u)

u = comanda sistem, marime de intrare(vine din exterior) si este legata de un anumit criteriu impus.

Ex. : o racheta trebuie sa fie in 2 pozitii succesive

x (0) = x₀ si la x (T) = x_T

comanda trebuie sa intervina astfel incat timpul parcurs sa fie minim

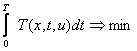sau

similar drumul parcurs trebuie sa fie minim = S

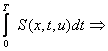min

3. Modele utilizabile pentru analiza unor situatii conflictuale

Presupune ca un sistem dinamic poate fi definit ca o functie de mai multe comenzi :

= f(x, t, u, v, w ...)

Pentru fiecare comanda avem anumite criteri:

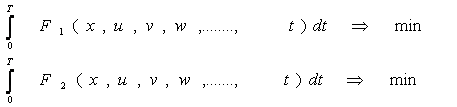
Functionalele sau criteriile definite concretizeaza interese diferite si este necesar ca peste criteriile date sa stabilim ierarhii si criterii decizionale. In cazul in care avem de-a

face cu un sistem cu implicatii umane este necesar sa deducem noi legi sau reguli care nu au fost evidentiale .

Aceasta problema s-a relevat in cazul simularii situatiilor de criza devenind esentiala pentru cazurile cand decizia depinde de experienta individului sau cand situatiile se pot modifica radical de la un moment la altul.

Exemplu : Deciziile in stari conflictuale sunt dificil de modelat si istoria arata o serie de cazuri in care prioritatile reale nu au fost respectate, fapt care a dus la accidente si catastrofe.

Un caz tipic este situatia de riposta a navelor americane imediat dupa razboiul din Golf, cand a fost doborat un avion civil irakian. Criteriile erau diferite pentru cei "3 actori" de pe o nava de lupta :

- comandantul navei

- ofiterul cu armamentul

- ofiterul care controla in mod general situatia navei

Din faptul ca nu s-au definit prioritatile ordinul de folosire a armamentului a fost dat si executat de ultimul "actor" care nu cunostea situatia generala conflictuala si care a interpretat aparitia unui avion ca o primejdie directa, actionind fara sa mai analizeze daca avionul este civil sau militar.

Caracteristici generale ale modelarii in domeniul simularii de aeronave

Simularea si respectiv modelarea matematica a aeronavelor presupune o serie de elemente caracteristice dintre care vom reaminti cateva:

1. - gradul de matematizare este definitoriu pentru cunoasterea si modelarea tuturor fenomenelor ce au loc in aeronava studiata.

2. - este specific crearea unui "arbore informational" care sa defineasca intrarile si iesirile esentiale pentru modelare.

3. - existenta posibilitatii de interventie rapide in programe : (setarea valorilor, sub-programe de rezolvare separate a ecuatiilor, posibilitatea inlocuirii rapide a unor algoritmi cu altii mai perfectionati)

4. - posibilitatea editarii de tabele de parametri specifici, de grafice tipice pentru a stabili corelatii specifice etc.

5.- necesitatea crearii unui model capabil sa fie rulat in timp real,adica la viteza derularii actiunilor pilotului in cazul aeronavei reale.

Simulatoarele de zbor prin complexitatea lor depasesc nivelul sistemelor automate simple utilizate de obicei in mediul industrial. Din punct de vedere a teoriei sistemelor ele pot fi incluse intr-o clasa foarte generala si anume in sisteme cu comanda adica sistemele sunt comandate din exterior pentru atingerea unor anumiti parametri si obtinerea unei situatii stabile.

Aceasta teorie a sistemelor comandate a fost dezvoltata foarte mult in anii 1960-1970 (legat de dirijarea rachetelor) si s-a perfectionat in special dupa aparitia calculatoarelor numerice, adica in momentul in care puterea de calcul a putut sa valorifice suficient modelele matematice.

Modelarea proceselor si obtinerea unui simulator corespunzator presupune 2 etape:

I. Modelarea cit mai adecvata a aeronavei pentru care urmarim simularea.

II.Optimizarea ansamblului de simulare si a tehnicilor utilizate: vizualizare, miscare, generarea de sunete etc. in vederea asigurarii aderentei cu aeronava reala.

Modelarea are si ea 3 etape care din pacate nu pot fi separate prin granite si care se intrepatrund functie de situatia dezvoltarii simularii respective.

Aceste 3 etape sunt :

1. identificarea caracteristicilor generale ale aeronavei care nu sunt explicite.

2. modelarea matematica a principalelor fenomene si sisteme aferente aeronavei, separarea modelelor dupa principiul functionalitatii.

generarea si crearea unui sistem de calcul care sa permita implementarea modelului si accesul la marimile de intrare si iesire caracteristice.

In continuare vom analiza in cadrul acestui capitol metode aplicabile in cazul unei aeronave clasice.

Identificarea modelelor

Dupa parcurgerea etapelor amintite in determinarea modelului matematic trebuie sa se exprime functionarea fiecarui sistem sau subsistem printr-un model matematic.

Aceasta etapa se numeste identificare si ea conduce la crearea pentru fiecare sistem sau subsistem de pe aeronava a unui model de functionare care sa descrie cit mai adecvat functionarea atit din punct de vedere static cit si din punct de vedere dinamic.Totalitatea acestor modele integrate formeaza modelul aeronavei care trebuie implementat intr-un sistem de calcul.

Problema dificila care necesita o atentie speciala in domeniul simulatoarelor este faptul ca nu exista pentru o serie de sisteme sau elemente din aeronava modele matematice.

O serie de dispozitive si sisteme (tren de aterizare, sistem de combustibil, modul de tranzitie la tragerea unei rachete) si alte multe evolutii nu sunt modelate matematic si deci trebuiesc analizate separat.

Din acest motiv este necesar sa se faca o identificare, deci sa se exprime matematic relatiile ce guverneaza sistemul.

Identificarea urmareste 2 aspecte :

- caracteristicile statice

- caracteristicile dinamice

De obicei caracteristicile statice sunt cunoscute din date de catalog sau se determina relativ simplu prin masuratori, pe bancuri de proba etc.Exista o intreaga literatura in acest domeniu si in general totalitatea dispozitivelor care se monteaza pe o aeronava raspund unor cerinte de calitate si sunt riguros testate si masurate.

Vom aminti metodele principale pentru determinarea caracteristicilor statice :

-metode directe=se determina caracteristicile sistemului sau agregatului prin aplicarea in mod deliberat la intrare de semnale alese si se masoara iesirile in regim stationar ;

-metode pasive=se numeste si metoda regresiei multiple,se folosesc variatiile marimilor de intrare in regim normal de functionare si rezultatele la iesire ;

-metoda experimentului factorial=se face un program special de modificare fortata a parametrilor de la intrare si se masoara marimile la iesire dupa un program.

Situatia dificila este cea din cazul caracteristicilor dinamice, deoarece este greu de prevazut ca s-au putut experimenta o serie de sisteme cum ar fi dirijarea unei aeronave in toate zonele de frecvente si la tot felul de marimi treapta.

Exista si un avantaj, existenta unor probe bine definite si care se fac la testarea aeronavei de catre pilotii de incercare prin inregistrari in zbor, conform regulamentelor aeronautice.

In aeronavele actuale situatia caracteristicilor dinamice este foarte importanta deoarece majoritatea sistemelor esentiale de comanda la bord sunt sisteme automate.Sistemele aeronautice ambarcate au inceput sa folosesc pentru controlul aeronavei piloti automati si sisteme de conducere a zborului din ce in ce mai perfectionate, dintre primele aplicatii fiind :

-autopilotul de pe BOEING 767 in 1986 ;

-calculatorul de bord de la F-16 dezvoltat de General Dynamics in 1984.

Dintre conceptele adoptate este interesant de amintit doua care au stat la baza proiectarii sistemeleor de comanda :

-primele sisteme au fost concepute pe baza unui model de variabile de stare autorul acestui sistem fiind R.Kalaman. Fata de sistemul clasic in care se anlizeaza marimile de intrare si iesire ale sistemului si se utilizeaza locul radacinilor,diagramele Bode si Nyquist pentru a verifica stabilitatea este esential ca se folosesc toate ecuatiile

sistemului si se calculeaza variatia tuturor marimilor pe intervale scurte de timp,operind in modelul neliniar al aeronavei.

-alegerea sistemelor de comanda functie de criterii de performanta globale si calculul comenzii functie de totalitatea variabilelor.Metoda permite datorita cresterii puterii de calcul la bord calculul tuturor marimilor de comanda a aeronavei in acelasi timp.Functie de o serie de criterii de stabilitate,reactie in timp etc,se determina structura

sistemului de comanda pentru o gama de evolutii si cu ce semnale se actioneaza in controlul aeronavei.

In ultimele decenii introducerea sistemelor de control digital a dus la posibilitatea de a controla simultan mai multe bucle de reglare si de a mari fiabilitatea sistemelor foarte mult.Este esential deci sa cunoastem comportamentul dinamic al sistemelor aeronavei.

In cazul determinarii caracteristicilor dinamice adica a modelarii raspunsului in timp si frecventa a comportamentului sistemelor la anumite marimi de intrare identificarea poate fi :

1. - analitica : numai prin legi fizice care se presupun ca se aplica in subansamlele studiate;

2. - experimentala : numai prin semnale de proba aplicate din exterior si masurarea si inregistrarea semnalelor de iesire

3. - identificarea mixta :se utilizeaza ambele metode pentru a optimizarea rezultatelor

Ce este esential la o identificare ?

1. - stabilirea marimilor de intrare si a marimilor de iesire

2. - stabilirea parametrilor specifici modelului

3. - interpretarea si prelucrarea rezultatelor experimentarii

4. - deducerea modelului - stabilirea structurii si a parametrilor

5. - verificarea si validarea modelului

Identificarea se poate face prin :

1. - identificare cu semnale de proba - metode active

2. - identificarea fara semnale de proba - metode pasive

3. - identificarea cu modele ajustabile

Identificarea cu semnale de proba deterministice periodice

Semnale ce se aplica la intrarea unui proces pot fi de cele mai variate tipuri. Pentru primele ipoteze se considera sistemele liniare si chiar monovariabile.

Semnalele de proba pot fi :

deterministe : - neperiodice : - impuls

- treapta

- periodice : - sinusoidale

- nesinusoidale

aleatoare

Aplicarea semnalelor pe sisteme depinde de sistemul respectiv :

daca este un sistem electric, electronic este indicat sa aplicam semnale periodice

daca este un sistem mecanic complicat e bine sa aplicam semnale de tip treapta sau impuls

Aplicarea de semnale de proba deterministice neperiodice

Se utilizeaza deci sisteme de excitare, de aplicare a semnalelor de tip treapta sau impuls si inregistratoare la intrare sau iesire sau traductoare, interfete si sisteme de achizitie si inregistrare de date.

Tipuri de semnale neperiodice pentru identificarea proceselor

Tipul semnalului	Reprezentarea lui in timp	Domeniul de aplicare
Impuls Dirac		Nu este realizabil practic
Impuls dreptunghiular		Procese cu elemente integratoare Procese in care nu se pot aplica marimi de intrare pe timp mare
t   x(t)   Impuls triunghiular		Procese cu elemente integratoare Procese cu frecvente medii
Impuls dreptunghiular dublu		Procese electrice - electronice Procese cu frecvente medii si inalte
t   x(t)   Functia treapta ideala		Procese fara elemente integratoare Precizie la frecvente joase
Functia treapta reala		Procese unde nu se pot aplica marimi bruste Procese cu frecvente joase

Amplitudinea semnalelor de proba este o marime importanta in determinarea caracteristicilor sistemului deoarece daca marimea de intrare este aleasa prost se poate forta procesul sa ia o turnura neliniara sa se satureze etc. Ideal este ca experimentul sa se faca intr-o zona mediana a procesului si se recomanda pentru amplitudinea semnalului de proba urmatoarea relatie :

A £ = amplitudinea semnalului de proba x_p

K_a = o valoare aproximativa estimativa a factorului

de amplificare a procesului de identificat

Daca asupra procesului actioneaza marimi perturbatoare de natura aleatoare de tipul x_p(t) care nu poate fi separata de marimea de iesire x_e atunci trebuie sa alegem pe A astfel incit sa percepem si influenta acestei marimi, deci sa facem determinari pe o durata de timp t_s mai mare decit durata perturbatiei.

Unele metode de deducerea modelului matematic

I. Cazul structurii necunoscute a elementului studiat :

Ipoteze : - nu exista componente oscilatorii

- modelul se considera liniar

O rezolvare in acest caz rezulta prin reprezentarea grafica a curbei experimentale y si apoi reprezentarea pe acelasi grafic a unei curbe cunoscute din literatura de specialitate yt.Prin integrarea suprafetei de diferenta dintre aceste doua curbe rezulta o marime ce trebuie minimizate.Se actioneaza prin iteratii asuprea parametrilor curbei cunoscute pina ce obtinem precizia necesara.

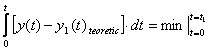
II. Cazul structurii cunoscute a elementului studiat

De obicei din cunoasterea structurii si a legilor fizice ce guverneaza procesul se poate accepta o functie care sa descrie cu aproximatie procesul. In consecinta se incearca aproximarea functiei de transfer cu ajutorul unor functii de transfer reprezentate in transformata Laplace tipice pentru automatica de forma:

Metoda este tipica pentru majoritatea aplicatiilor legate de :

- fenomene de actionari hidraulice sau electrice

- fenomene de reglari termice

-actionari de elemente aerodinamice etc

Daca sistemul prezinta existenta unui 'timp mort' adica o diagrama de raspuns de tipul din figura in care marimea de iesire reactioneaza dupa un anumit timp la aplicarea unui semnal de tip treapta la intrare atunci functia de transfer se poate deduce experimental pe baza trasarii diagramelor din figura urmatoare:

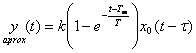
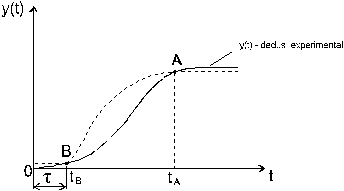
K = rezulta din regimul stationar si se poate masura direct pe diagrama

t = timp mort pe cale grafica

se determina prin impunerea ca raspunsul in timp sa coincida in

doua puncte cu raspunsul indicial deci se aleg punctele A si B.

Identificarea cu semnale de proba deterministe periodice

Semnalele de proba deterministe si periodice pot fi de doua tipuri :

1. - sinusoidale

2. - dreptunghiulare

Cele sinusoidale sunt tipice si frecventa lor trebuie sa acopere banda semnalelor tipice ale fenomenului.

Daca se utilizeaza cele dreptunghiulare se aplica apoi dezvoltarea in serie Fourier a lor si se pun in evidenta componentele din care cea mai importanta este fundamentala si apoi armonicele.

Exista calculatoare specializate ce determina pe baza unor semnale sinusoidale functia de transfer :

- la intrare se genereaza 2 functii sinusoidale :

A_i sin wt

A_i cos wt

- la iesire rezulta caracteristicile de frecventa :

Re H(jw) sau A (w)

Im H (jw) j (w)

Schema bloc a unui astfel de aparat este :

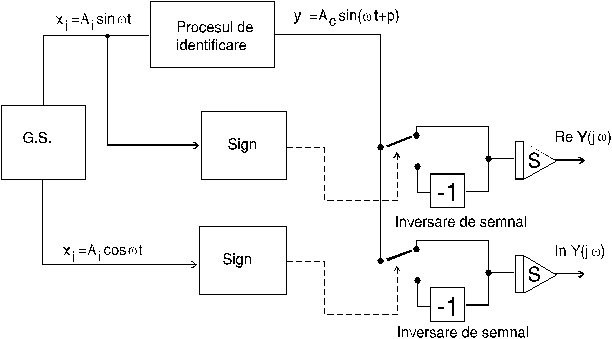
se extrag deci partile imaginare si partile reale din functia de transfer ce este real y(t) sing x_i (t)

ce este imaginare y(t) sing x_i

si apoi se integreaza pe intervalul 0, T

Identificarea cu modele ajustabile

- metodele de identificare cu modele ajustabile sunt larg folosite in aviatie pe modele functionale adica pe sisteme aeronautice montate la sol pentru testare si in special in simulatoare.

Fizic se realizeaza un model cu parametrii ajustabili care se conecteaza in paralel cu procesul de identificat.

La intrare se aplica aceleasi marimi de intrare si se compara si se inregistreaza marimile de iesire din model si din proces in raport cu un criteriu de eroare :

- se impune un anume criteriu = eroarea medie patratica minima

I =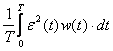

sau - aproximarea cu functii obtinute prin dezvoltare in serie Taylor

sau - estimare cu functii tipice fenomenului.

Daca modelele au prioritatea de a acumula informatii pe care le utilizeaza pentru perfectionarea procedurii de adaptare a modelului se numesc modele instruibile si cu memorie. Avantaj este ca procedura este rapida sin nu afecteaza procesul.

Modele matematice ale avionului

Structura caracteristica a modelului matematic

Se va analiza pe scurt complexitatea sistemica a aeronavei, a sistemului si a elementelor specifice care trebuiesc modelate. Pentru o aeronava, in conformitate cu o schema clasica (ETKIN.B. - Dynamics of Atmospheric Flight - J.Wiley - N.Y. - 1972) elementele ce influenteaza zborul si dinamica sa sunt :

REACTII UMANE IN PILOTAJ

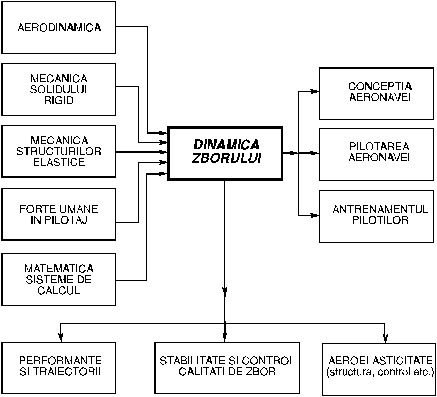
Locul simulatoarelor in aceasta diagrama este aparent periferic, dar avind in vedere gradul ridicat de raspundere, faptul ca vitezele si puterea motoarelor a crescut de citeva ori in scurta istorie a aviatie, iar traficul a atins valori extraordinare, locul acestora s-a mutat catre centru, antrenamentul la sol al pilotilor avind o importanta foarte nare. Simulatorul de zbor din punct de vedere sistemic si al parametrilor care sunt vehiculati reprezinta una dintre marile realizari ale ingineriei, atit din punct de vedere tehnic cit si a efectelor economice.

Analizind domeniile de stiinta care intervin in conceptia modelului matematic al unui simulator de zbor, observam cu usurinta ca domeniile sunt extrem de variate si ca fara o puternica dezvoltare a tehnicii de calcul realizarea de astfel de produse ar fi fost imposibila.

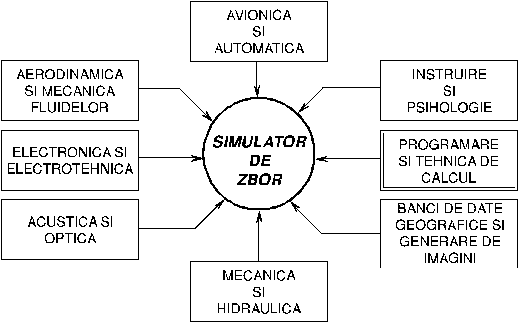
Toate aceste domenii determina metode de investigare, tehnici de calcul specifice, moduri de reprezentare diferite si precizii partculare dar participa la functionarea in timp real a acestui sistem.

Din punct de vedere a modelului matematic si totodata sistemic, simulatorul se compune din diferite subsisteme care fie ca functioneaza separat si exista ca entitate fizica, fie ca sunt in totalitate incluse modelat in sistemul de calcul.

In privinta amplasarii fizice a diferitelor elemente, variantele constructive au progresat in timp de la simulator la simulator. In general, exista insa 2 variante clare :

1. varianta cu postul instructorului amplasat pe platforma mobila, la fel si elementele specifice sistemului de calcul, este o varianta tipica pentru elicoptere si avioane de transport;

2. varianta cu postul instructorului amplasat la sol in afara platformei mobile si sistemul de calcul tot la sol, varianta aplicata pentru avioanele scoala si militare.

Functionarea simulatorului este clar descrisa prin magistralele de date si informatii care sunt prezentate in figura. Esential, pentru aceasta etapa a studiului este modul de legatura intre sisteme nu felul cum sunt ele dispuse in mod fizic,la fel deimportant este daca se pot defini modelele necesare pentru a realiza o structura de calcul eficienta si complecta.

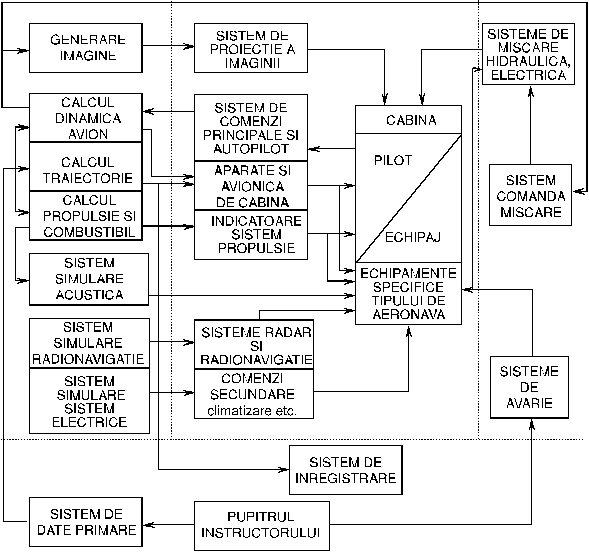
Facind o evaluare rapida si generala a modelelor necesare, rezulta ca unele sunt absolut necesare si ca altele influenteaza, dar cu o pondere minora.

Modelele esentiale in cazul simularii sunt:

1 - modelul atmosferei standard

2 - modelul aerodinamicii avionului

3 - modelul comenzilor de zbor/autopilot etc./sistem hidraulic, etc.

4 - modelul de rulaj la sol, modelarea trenului de aterizare

5 - modelul sistemului de propulsie

6 - model de gravimetrie/centraj/date inertiale/configuratii etc.

7 - modelul sistemului de radionavigatie

8 - model pentru aparate si semnalizari/avionica/afisare etc.

9 - model pentru sistemul de combustibil - regim dinamic

10 - model pentru referentiale si matrici de trecere

11 - model pentru situatii de avarii complexe

Din punct de vedere a timpului de rulare pentru fiecare model ele se pot caracteriza ca fiind de 2 tipuri:

- modele rapide care se selecteaza de la sine prin frecventele proprii ridicate de variatie a parametrilor si prin necesitatea de a influenta direct imaginea, miscarea;

- modele lente care au efect integrator gen: traiectorie, combustibil etc,, in care datele nu influenteaza direct decizia dinamica zborului.

Deci necesitatea calculului in timp real apare pentru o serie de marimi bine definite care influenteaza direct simularea zborului aeronavei si anume :

- marimi necesare pentru atitudinea avionului : sistem de imagine, miscare;

- marimi necesare pentru alimentarea cu date a avionicii din cabina;

- marimi necesare pentru sistemul de propulsie, sunet, tractiune etc.;

- marimi necesare a fi afisate la pupitrul instructorului pentru controlul antrenamentului;

- marimi legate de structura de calcul si model in general : regim de rulaj la sol, desprindere, trecere de la un regim de zbor la altul, trecere de la subsonic la supersonic etc.

Dintre marimile care activeaza ca marimi de intrare, mentionam ;

- marimi induse de catre pilot - comenzi de zbor, comenzi logice;

- marimi induse de catre instructor - optiuni de zbor, date initiale, date geografice etc., comenzi declansatoare de regimuri speciale avarii, inghetari ale exercitiului etc.

Se va grupa acest domeniu in doua subdomenii pentru a simplifica expunerea

- modelul aerodinamic

-modele conexe.

Modelul aerodinamic al avionului

Esential pentru constructia unui model adecvat este :

aplicarea corecta a relatiilor fundamentale ale aerodinamicii

utilizarea aditiva a datelor experimentale :

- date de tunel

- date obtinute prin similitudine cu aeronave din aceeasi clasa

- date obtinute experimental prin experimentari in zbor

In general sarcina celui care elaboreaza un model aerodinamic pentru simulator este mai simpla decit a unui constructor de aeronava deoarece se realizeaza modelul unei aeronave definite,construite si testate.In consecinta exista un volum mare de date accesibile.Problema dificila este :determinarea unor coeficienti care nu sunt utilizati in aerodinamica curenta pentru o serie de evolutii acrobatice ale aeronavei si incadrarea efectuarii calculelor pe model intr-o zona de timp similara cu dinamica aparatului de zbor.

Modelele aerodinamice sunt des folosite si in alte domenii dintrer care amintim :

pentru a perfectiona design-ul unui avion existent si a aduce perfectionari in timp

pentru evaluarea performantelor unui prototip

pentru a reconstitui accidente,cazuri de avarie de sisteme etc.

Vom reaminti citeva generalitati din aerodinamica pentru a ajunge la ecuatiile de baza.

In cazul unui avion clasic cu aripi simetrice, ampenaj si elemente de comanda profilul si geometria aripii este definitorie pentru performantele aeronavei .Se vor defini fortele si momentele si triedrele de referinta.(Notatiile folosite vor fi cele din literatura anglo-saxona)

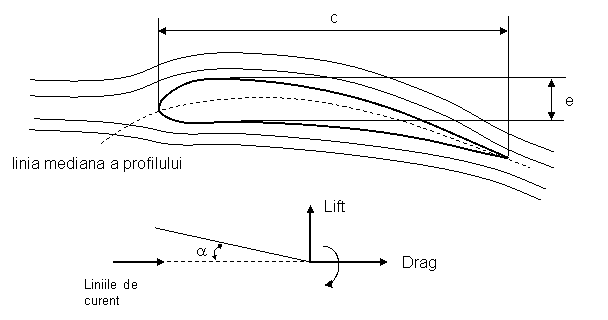
= unghiul de incidenta al aripii

c = coada profilului

e = grosimea profilului

Se considera o serie de marimi semnificative:

centrul aerodinamic = punctul in care momentul generat de fortele aerodinamice ce actioneaza asupra profilului este aproape invariant cu valoarea lui a

aeronava poate fi stabila sau nu dupa pozitia si profilul aripii, rezulta deci ca se poate optimiza prin o serie de incercari de tunel si se va putea astfel determina daca avionul este sau nu stabil la anumite viteze si unghiuri de incidenta.

Fortele care actioneaza asupra profilului de aripa plasat intr-un curent de aer cu o anumita viteza sunt forte ascensionale L si forte de rezistenta la inaintare D.Ele genereaza si un moment al profilului denumit M.

Profilele aripilor se obtin prin mai multe metode :

profile teoretice - prin aplicarea unor transformari conforme unor functii

profile empirice - prin trasare libera si apoi prin experimentare

profile generate prin metoda inversa- adica plecand de la distributii de presiuni impuse si generind geometria

Totodata aeronavele se clasifica dupa numarul Mach ce defineste raportul dintre viteza aeronavei si viteza sunetului in conditii de atmosfera standard.

Aeronavele se clasifica in :

-aeronave subsonice care evolueaza cu M< 1

-aeronave transonice care evolueaza la 0,8<M<1

-aeronave supersonice care evolueaza la 1<M<5

-aeronave hipersonice care evolueaza la M>5

O alta selectie se face dupa modul propulsiei care poate fi :

-cu elice

- cu motor reactiv

-cu un motor sau cu mai multe motoare

Ipoteze de calcul pentru modelul ce va fi prezentat :

- se va trata modelul unui avion cu elicie cu comenzi clasice neasistate

- regimul de zbor este subsonic si se face totodata ipoteza Pamintului plat

- aeronava este rigida si distributia de masa in aeronava este constanta

- planul XZ este un plan de simetrie pentru aeronava

Sisteme de axe asociate

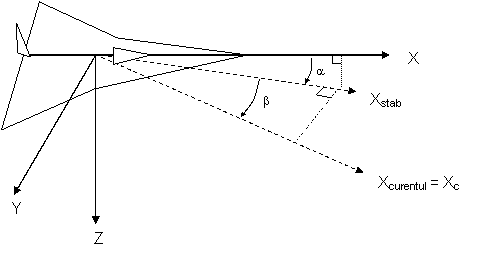
Vom defini triedrele asociate cu aeronava si avind originea in centrul ei de greutate si doua unghiuri specifice :

X=axa asociata componentei longitudinale a aeronavei avind sensul pozitiv catre exterior.

Y=axa asociata aripii drepte si cu sensul pozitiv catre exterior

Z=axa asociata directiei in jos, ortogonala celorlalte axa si cu sensul pozitiv catre exterior

Functie de directia curentului de aer in care evolueaza aeronava se definesc si doua unghiuri :

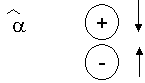
a = unghiul de incidenta- este unghiul dintre directia de curent a fluidului si axa X

b = unghiul de derapaj -este unghiul dintre directia de curent si directia stabilizata de evolutie laterala a aeronavei

X, Y, Z =sunt axe asociate cu structura aeronavei

b

X_stab    = axa stabilzata

a miscarii aeronavei

X_c = axa curentului de aer

Se definesc si cele sase grade de libertate ale aeronavei :

-trei translatii dupa axele X,Y,Z

-trei rotatii in jurul acelorasi axe unghiurile fiind definite ca unghiurile Euler.

Fortele aerodinamice sunt corespunzator axelor:

L - forta ascensionala    - L

D - rezistenta la inaintare - D

Y - forta laterala - Y

Trecerea marimilor vectoriale de la triedrul asociat avionului la triedrul asociat curentului de aer se face prin doua matrici de transformare ce depind de unghiurule de incidenta si de derapaj.ansformarea

Prima transformare a fost cea descrisa de marticea de mai sus.A doua este definita de urmatoarea matrice :

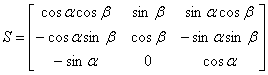
Combinind cele doua transformari se obtine trecerea de la un triedru al celalalt pentru orice vector cu maticea S :

Deci pentru componentele fortelor se poate scrie transformata :

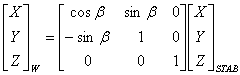
Deci cu transformarea S trecem de la vectorii asociati curentului de aer stabilizat la vectorii asociati aeronavei.

Definirea fortelor si momentelor

Se considera ca fortele si momentele ce se exercita asupra aeronaveiau doua cauze :efecte aerodinamice generate de efectul curentului de aerasupra configuratiei aeronavei si de efectul datorat tractiunii elicii.Vom utiliza o serie de indici inferiori

Efecte aerodinamice si tractiunea motorului

Indice A Indice T

Cu aceste notatii fortele asupra aeronavei se descompun astfel:

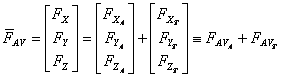
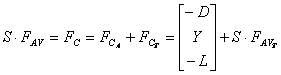
Momentele ce actioneaza asupra aeronavei sunt descompuse in trei componente :   

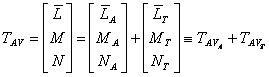
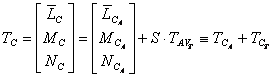
La fel ca si in cazul fortelor aerodinamice s-a aplicat descompunerea momentelor in momente datorate aerodinamicii si momente

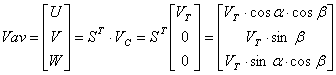
Din ultima expresie a vitezei rezulta ca :

Legatura dintre forte, momente si coeficienti aerodinamici

Pentru a exemplifica legatura dintre aerodinamica aeronavei si viteza curentului de aer in care aceasta evolueaza se introduc notatiile :

= presiunea dinamica a curentului de aer

S = suprafata de referinta a aripii

b = anvergura suprafetei aerodinamice

= coada medie geometrica a aripii

Cu aceste notatii rezulta expresia fortelor care actioneaza asupra aeronavei :

Toti coeficientii de clasa C au fost definiti functie de caracteristicile aerodinamice ale aeronavei.

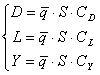
Similar se obtine expresia momentelor aeronavei pentru cele 3 axe functie de coeficientii aerodinamici de moment.

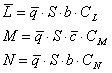
Pe langa acesti coeficienti se pot utilizeaza si coeficienti specifici :

C_x, C_y, C_z -legati de aeronava si de axele proprii

Coeficientii amintiti sunt dependenti de o multitudine de factori, dar cei esentiali pentru modelarea urmarita sunt :

- a

- b

- nr. Mach al evolutiei

Pentru un avion subsonic ponderea componentelor este :

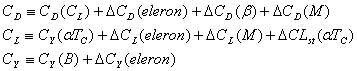
Curbele tipice pentru aceste dependente se obtin prin 3 metode :

metode de calcul

metode experimentale in suflerii

metode experimentale combinate (sufleriei + real)

Exemple :

M = numarul Mach de zbor

Graficul coeficientul de rezistenta la inaintare functie de coeficientul de portanta poarta numele de polara si este foarte importanta, fiind de fapt o familie de curbe avind numarul Mach ca parametru.

	M =numarul Mach in evolutia de zbor

Modelarea matematica a acestor curbe poate fi data de ecuatia parabolica :

C_DM - coeficientul minim de rezistenta la inaintare - apare la o valoare a lui neegala cu zero.

Pentru a modela in mod real se adauga termeni de corectie cate tin cont de configuratia reala a aeronavei : flapsuri, tren, rezervoare suplimentare etc., efect de sol, compresibilitate etc.

C_L

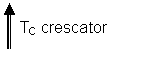
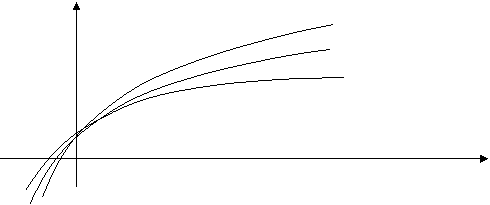
2.Coeficientul de portanta C_L

Acest coeficient depinde de a si de T_C

a = unghiul de incidenta

T_C= coeficient de tractiune,T=tractiunea datorata eliciei cu aria S

    Din aceste doua exemple simple rezulta faptul ca descrierea fortelor si momentelor aerodinamice formeaza o baza de date tipica pentru o aeronava data.

De obicei este vorba de 100 de tabele mai mult sau mai putin complexe. O astfel de baza de calcul este insa formata in mii de ore de calcul, testare pe model, testare in zbor si simulare pe calculator.

Problema care apare este ca datele aerodinamice sunt discrete, pe o serie de portiuni se linearizeaza in timp ce modelele utilizate in simulatoare cer date si valori pentru toate manevrele posibile.

Aceasta problema se rezolva prin algoritme de interpolare si structuri de model variabile.

Modelul aeronavei

In modelul prezentat anterior se vor ingloba fortele si momentele aerodinamice cautand sa obtinem un sistem de ecuatii care sa descrie comportarea aeronavei in 6 grade de libertate si sa obtinem si o serie de legaturi de comanda.Trebuie sa precizam de la inceput ca modelul este neliniar .Caracterul neliniar rezulta din faptul ca o serie de marimi si cantitati se modifica in raport cu timpul, iar o serie de coeficienti si functii contin functii neliniare si trigonometrice.

Elementele ce vor fi urmarite in calcul sunt :

-vectorul viteza al aeronavei V_AV

-vectorul unghiurilor Euler F

-vectorul rotatiilor w_AV

-vectorul de pozitie (de navigatie) fata de Pamint.

Deci vectorul de stare al aeronavei este descris prin urmatoarele componente :

p_N = pozitia fata de nord

p_E = pozitia fata de est

h = pozitia fata de suprafata pamantului

Setul de ecuatii e compus din 12 ecuatii care se scriu sub forma :

Ecuatiile de forte care arata echilibrul fortelor aerodinamice, inertiale si datorate gravitatiei:

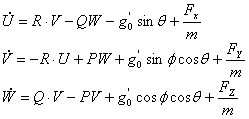
Ecuatiile cinematice leaga vitezele unghiulare de P,Q.R.

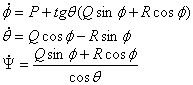
Ecuatiile momentului

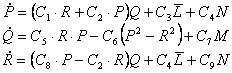
In ecuatia de momente s-au folosit urmatoarele notatii :

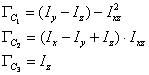
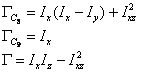
Ecuatiile de navigatie sunt :

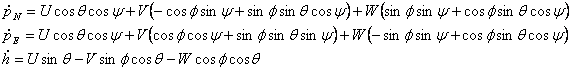
Pentru a putea utiliza acest model compus din 12 ecuatii se mai efectueaza o serie de complectari la acest model :

1. componentele F_x, F_y, F_z, L, M, N se pot separa in contributii datorate aerodinamicii si contributii datorate tractiunii.

2. se adauga si tabele cu dependenta tractiunii cu altitudinea si cu viteza (Mach) cu pozitia manetei de gaze ca parametru.

3. un numar de forte aerodinamice si componente de moment contin dependenta de o serie de suprafete de control si vectorul de intrare in model este :

Se specifica ca : sunt componentele vitezei fata de locul geografic de pe triedrul asociat Pamantului.

pozitie pozitie pozitie pozitie

U^T = manete eleron deriva carma

de gaze

In diferitele prezentari a acestui model neliniar este important sa se evalueze marimi specifice legate de modelare si implicit de simularea aeronavei care este scopul final.

Fortele si momentele din sistemul de ecuatii prezentat depind de :

-unghiurile aerodinamice ale aeronavei

-viteza adevarata a aeronavei

Deci este important sa se inlocuiasca variabilele de stare : U, V, W prin V_T, b a

Din ecuatiile de forte putem sa determinam expresiile noilor derivate de stare :

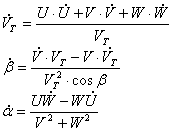
Noul vector de stare este acum scris sub forma in care putem defini clar pozitiile aeronavei:

O solutie a acestor ecuatii este data de un set de valori care pentru un anumit punct de pe traiectorie satisfac si verifica ecuatiile.

Procesul de a gasi o astfel de solutie este usurat prin utilizarea unui calculator specializat.

Programe speciale de calcul efectueaza integrarea acestor ecuatii pentru esantioane scurte de timp deci cu pas de integrare variabil.

Metodele tipice de integrare sunt :

-metoda dreptunghiurilor(Euler) ;

-metoda trapezelor ;

-metoda Runge-Kutta.

Utilizatorul va alege intervalul de timp de integrare in asa fel incit sa fie optim atit pentru precizia necesara in procesul simularii cit si pentrugradul de reprezentare a solutiilor.

Avantajul mare este ca se pot obtine rapid diverse grafice privind evolutia aeronavei si se compara rapid datele astfel obtinute cu date din graficele tipice testarii aeronavei reale.Multi din factorii cu pondere mica se elimina.

Una din dificultatile care apare este :

-coeficientii de forte aerodinamice depind de si , iar noi nu putem sa calculam aceste derivate decat dupa ce aflam fortele.

Rezolvarea acestei situatii se face prin alegerea altor axe de coordonate.

Etapele de calcul in care dorim totusi sa folosim acest model sunt :

Dinamica aeronavei este studiata tot cu ajutorul ecuatiilor amintite in care se considera ipoteza micilor perturatii adica pentru situatii in care sistemul om-comenzi -aeronava sau om-sistem automat de comenzi -aeronava poate sa mentina zborul in conditii sigure pastrind directia stabilita.

Ecuatiile de stare sunt de forma :

dX=AX+Δfc

dX=vectorul de stari al aeronavei

A=o matrice de coeficienti caracteristici aeronavei dar constanti

Δfc=vectorul de comanda a fortelor si momentelor ce actioneaza asupra aeronavei

care in cazul nostreu este egal cu zero.Ecuatia devine astfel :

^dX=AX

Rezulta solutii de tipul :

x(t)₌x_oe^λt

in care

X=vectorul de valori proprii,

=valoriile proprii ale sistemului

X =X(t=0)

Ecuatia caracteristica are in general N solutii i adica valori proprii si fiecarei valori proprii ii corespunde un vector propriu Xo

X(t)=Σ_i x_oi e^λ_i ^t

Fiecare solutie este o solutie naturala.

Cu ajutorul unor programe specializate care se gasesc in multe aplicatii matematice se pot calcula valorile proprii si vectorii valorilor proprii.

Aplicarea unor criterii de stabilitate tipice cum ar fi criteriul de stabilitate Routh determina daca aeronava este stabila pentru o serie de evolutii care se incadreaza in

teria micilor perturbatii.

Prin setarea comenzilor se pot calcula stari dinamice stabile ale evolutiilor si momente tipice pentru aeronava.

In cazul unor valori mari de schimbare a comenzilor sau modificari ale unghiurilor aeronavelor,ale vitezei etc vor apare schimbari mari ale coeficientilor aerodinamicii si ale fortelor si momentelor fapt care va duce la nelinearizarea modelului.

In aceasta situatie se vor aplica pe zone metodele de integrare tipice care au fost amintite si se va face integrarea pe portiuni ca in algoritmul prezentat anterior.

Derivatele care sunt folosite in acest model Newtonian se impart in 3 categorii :

-derivate statice care includ derivatele fortelor si momentelor fata de

-derivatele dinamice care includ derivatele fortelor si momentelor fata de variatiile in timp ale marimilor α,β, p,q,s,

-derivate de comanda datorita actiunilor de comanda ce actioneaza in model.

Numarul de derivate este foarte mare in modelul definit, dar ponderea lor este diferita si pe baza experimentarilor si evaluarilor efectelor se pot elimina foarte multe.

In cazuri concrete cum ar fi miscarea de tangaj a aeronavei in ipotezelel mentionate pentru a usura calculele se aplica metoda micilor perturbatii introdusa de G.H.Bryan adica se considera ca pe mici portiuni modelele sunt lineare in cazul conditiilor de zbor echilibrate.In consecinta ecuatiile neliniare in coeficienti devin liniare iar coeficientii se pot deduce pe portiuni mici prin iteratii.Pentru sistemele de calcul ale simulatoarelor metoda prezinta multe avantaje deoarece se poate opera in timp real cu tabele de coeficienti si iteratii cu pasi stabiliti din aproape in aproape.

Etapele de calcul sunt urmatoarele :

Modele conexe ale avionului

Pe linga o serie de modele principale cum ar fi modelul aerodinamic si modelul comenzilor in calculele de simulare apar si o serie de modele conexe ale aeronavei :

- modelul trenului si a rulajului la sol

- modelul sistemului de propulsie

- modelul de aparate si radionavigatie

- modelul de combustibil si centraj

Fiecare din aceste modele nu au o complexitate similara cu cel al modelului aerodinamic, dar trebuie sa intervina in modelul general si contribuie la fidelitatea simulatorului.

In capitolul de fata vom analiza citeva din aceste modele pentru a putea considera modul de calcul si structura lor.

Manevrele aeronavelor se trateaza in cazul simulatoarelor moderne pornind de la toate etapele de pregatire a aeronavei astfel incit si aceste modele au rolul lor perfect definit.

Modelul rulajului la sol

Introducem o serie de notatii specifice rulajului la sol :

R₁, R₂ = raza rotii trenului

a = unghiul de incidenta

a_T = unghiul dintre axa tractiunii si axa 0x

Date geometrice :

x₁, x₂ = proiectia orizontala a distantei dintre centrul de greutate si axa rotii

z_G = proiectia verticala a pozitiei centrului de greutate

z₁, z₂ = proiectia verticala a distantei dintre centrul de greutate si axa rotii

l_a = distanta dintre axa rotilor principale si cea a rotii din fata (ampatamentul - ecartamentul aeronavei)

z_T = proiectia verticala a distributiei dintre centrul de aplicare a fortei de tractiune si centrul de greutate

Forte si momente

L = P = forta portanta;

D = rezistenta aerodinamica la inaintare

T = forta de tractiune

G = greutatea avionului

m = masa avionului

F = forta de franare (F₁, F₂ - roti si jambe anterioare)

momentele aeronavei de ruliu, giratie azimut (cap)

M_f = momentul de franare

N₁ = fortele normale pe jamba de bot

N₂ = forta normala pe jambele anterioare

q = viteza de tangaj

Centrul fortelor de franare se face astfel :

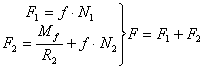
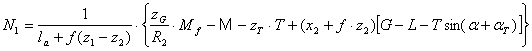
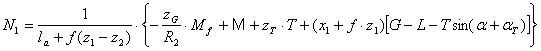
Ecuatiile de miscare ale aeronavei se simplifica pentru rulajul de sol si au expresia :

unde: d(V) = comanda de tren (scos / decolare/ aterizare)

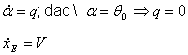
O alta conditie este ca la decolare :

M_f = 0, adica sa nu se franeze

Pe baza acestor relatii se stabilesc regimurile de decolare si aterizare si modul de trecere de la regimul de rulaj la sol si la modelul de zbor.

Modelul aerodinamic de zbor la joasa inaltime este laborios si comporta o serie de coeficienti specifici care includ efectul de sol si alti factori.

Modelul de calcul al masei aeronavei

Aparent este un caz extrem de simplu, dar in realitate cei care se ocupa cu simularea nu au un calcul de mase extrem de precis, de aceea se face un calcul de estimare dupa o serie de formule empirice, dar care dau bue rezultate in practica.

In general, se considera o serie de relatii statistice valabile pentru aeronave, fiecare element fiind raportat la masa generala la decolare :

1. aripa 10

2. ampenajele . 1,8

3. fuselajul.. 6

4. trenul de aterizare. 4 8%

5. masa utila.. 8

6. combustibil. 23

Pentru a putea insa sa calculam efectiv aceste valori in dimensionarea unui tip anumit de aeronava trebuie sa facem apel la formule mult mai clare.

Calculul masei aripii

O prima relatie simpla de estimare a masei aripii m_a e data in literatura de specialitate sub forma :

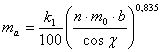
unde:

k₁ = -0,9991 pentru avioane cu piston

-1,0185 avioane cu motoare aeroreactoare pentru distate mici

-0,9215 avioane cu motoare aeroreactoare pentru distate mari

n = factorul de sarcina de calcul

m₀ = masa totala la decolare

b = lungimea aripilor

cosc = cosinusul unghiului de sageata al sarnierei.

O alta relatie specifica este cazul calculului aripii ca suma a doi termeni : masa structurii propriu-zise si a sistemului de hipersustentatie :

m_sa = masa structurii propriu-zise este influentata de :

- lungimea aripii

- coeficientul (factorul de sarcina)

- masa aeronavei

- unghiul de sageata al sarnierei

- numarul de motoare de pe aripa

- grosimea profilului

- daca trenul se escamoteaza sau nu in aripa

m_sh = masa sistemului de hipersustentatie este dependenta de :

- masa voletilor de bord de atac

- masa sistemelor de actiune

- suprafata mecanizata din aripa

Calculul masei fuselajului

O formula rapida de calcul este :

in care :

a = 0,0030 . 0,0094 - functie de numarul de motoare si amplasarea lor

b - functie de numarul de motoare si amplasarea lor

Calculul masei ampenajului

Masa ampenajului orizontal este estimata cu ajutorul relatiei :

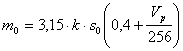
in care :

s₀ = s_o1+s_o2= suprafata totala a ampenajului

V_p = V_picaj - pentru avioane de lupta

V_p = V_croaziera +113km/h

k = 1,2

Masa ampenajului vertical e data de formula :

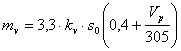
in care :

k_v = 1,5 pentru ampenaj in "T"

s₀ = suprafata totala a ampenajului

Calculul masei sistemului de propulsie

Masa este data clar in cataloagele de motoare si in ea se includ si masa sistemului de evacuare, de racire si de ungere. Pe langa acestea se adauga si masa sistemului de admisie, masa sistemului de combustibil si a comenzilor motorului.

Factorii ce influenteaza sunt :

- forma prizei si amplasarea (materialele)

- numarul prizelor

- presiunea statica la intrarea in compresor

- nr. Mach in zbor orizontal al avionului

Pentru combustibil exista relatii statistice :

C = cantitatea de combustibil in litri

G₀ = greutatea la decolare a avionului (daN)

D = distanta de zbor exprimata in km.

De regula intre masa aeronavei si masa de combustibil exista o legatura simpla:

m_combustibil 0,50)m_{aeronavei la decolare}

Toate aceste modele sunt integrate intr-un program general care descrie functionarea aeronavei in majoritatea evolutiilor.