SISTEME DE COMUNICATII PENTRU TRANSPORTURI

SISTEME DE COMUNICATII PENTRU TRANSPORTURI

Puterea si energia semnalelor

1. Obiectivul lucrarii

In aceasta lucrare, se studiaza puterea si energia semnalelor.

2. Introducere teoretica

Puterea si energia

Prin definitie, energia unui semnal real , notata cu , este expresia

Puterea semnalului are expresia:

Un semnal cu energie finita se numeste semnal de tip energie. Un semnal cu putere finita si pozitiva se numeste semnal de tip putere. Exista semnale care nu apartin nici uneia din aceste doua clase. Un exemplu de semnal de tip energie este iar un exemplu de semnal de tip putere este x(t) = cos(t). Toate semnalele periodice sunt de tip putere. Densitatea spectrala de energie a unui semnal de tip energie ne da distributia de energie la diverse frecvente ale semnalului si are expresia

De aceea,

Pentru valori reale ale semnalelor, definim functia de autocorelatie a lui astfel:

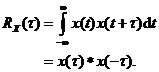
Utilizand teorema convolutiei, avem

Pentru semnale de tip putere, definim functia de autocorelatie mediata in timp astfel:

Densitatea spectrala de putere este in general data de

Puterea totala este integrala densitatii spectrale de putere, data de

Pentru cazul particular al unui semnal periodic cu perioada si coefi-cientii seriei Fourier densitatea spectrala de putere este data de

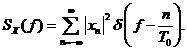
Aceasta inseamna ca toata puterea este concentrata la armonici ale frec-ventei fundamentale si ca puterea la armonica    a n-a este , adica, modulul coeficientului corespunzator al seriei Fourier la patrat.

Daca semnalul trece printr-un filtru cu functia de transfer densitatea spectrala de energie a iesirii si densitatea spectrala de putere se obtin prin relatiile

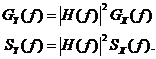
Daca utilizam semnalul esantionat (adica, in timp discret), energia este data de expresia:

Puterea este data de

Daca se utilizeaza transformata Fourier rapida TFR, adica, daca lungimea sirului este finita iar sirul se repeta, avem

Functia MATLAB power.m ne da continutul de putere al unui vector de semnal.

Function p=spower(x)

p=spower(x)

%SPOWER returneaza puterea din semnalul x

p=(norm(x)^2)/length(x);

Daca este transformata Fourier discreta a unui sir densitatea spectrala de energie a lui semnalul analogic echivalent, se obtine utilizand ecuatia

pentru (vezi lucrarea de laborator precedenta) si este data de

unde este intervalul de esantionare. Densitatea spectrala de putere a unui sir se poate obtine cu usurinta utilizand functia MATLAB spectrum.m.

Problema

Puterea si spectrul de putere

Semnalul are o durata de 10 si este suma dintre doua semnale sinusoidale de amplitudine egala cu unu, primul cu frecventa de 47 Hz si al doilea cu frecventa de 219 Hz:

Acest semnal se esantioneaza cu o frecventa de esantionare de 1000 de esan-tioane pe secunda. Sa se utilizeze MATLAB pentru a gasi continutul de putere si densitatea spectrala de putere pentru acest semnal.

Rezolvare

Cu ajutorul functiei MATLAB spower.m, gasim ca puterea semnalului este egala cu 1,0003 W. Utilizand spectrum.m si specplot.m, putem reprezenta grafic densitatea spectrala de putere a semnalului asa cum se arata in     figura 1. Cele doua maxime locale din spectrul de putere corespund celor doua frecvente prezente in semnal.

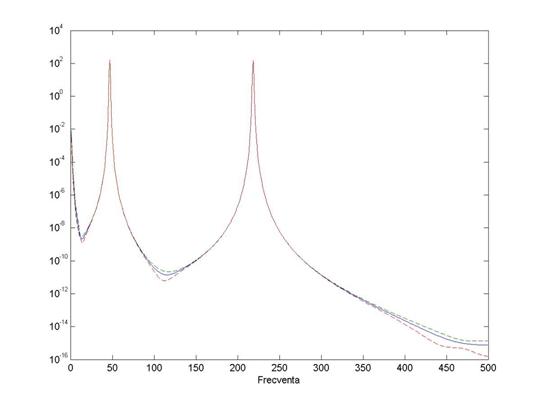
Figura 1. Densitatea spectrala de putere a semnalului constand din doua semnale sinusoidale de frecvente = 47 Hz si = 219 Hz.

Programul MATLAB pentru aceasta problema este dat mai jos.

% Programul MATLAB pentru problema.

ts=0.001;

fs=1/ts;

t=[0:ts:10];

x=cos(2*pi*47*t)+cos(2*pi*219*t);

p=spower(x);

psd=spectrum(x,1024);

pause % apasa orice tasta pentru a vedea puterea din semnal.

p

pause % apasa orice tasta pentru a vedea spectrul semnalului.

specplot(psd,fs)