| CATEGORII DOCUMENTE |
| Aeronautica | Comunicatii | Electronica electricitate | Merceologie | Tehnica mecanica |
Sunt trei tipuri de zgomote specifice M.D.:
zgomotul de cuantizare
zgomotul de depasire a pantei
zgomotul de pauza.
1. Calculul zgomotului de depasire de panta Zd.
Deoarece Zd >> Zc la calculul Zd se neglijeaza contributia Zc.
![]()
![]()
 Es
Es
 D
D
A
![]() y(t)
y(t)
![]()
![]() kp (k+1)p 2pfst
kp (k+1)p 2pfst
![]()
![]() 2pfstA
2pfstA
q x(t)
![]()
![]()
![]()
![]() C F B
C F B
![]()
q+p
![]()
F+p
Pentru un semnal
de intrare de forma ![]() depasirea este
inlaturata daca
depasirea este
inlaturata daca ![]()
In cazul neindeplinirii conditiei de urmarire incepe depasirea de panta (exemplu pct.A).
Panta semnalului x in pct. A este:
![]() cu conditia k=par
cu conditia k=par
In acest punct
cele doua pante sunt egale : ![]() .
.
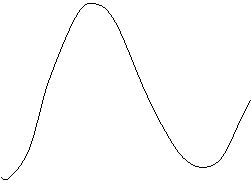
Pe tot timpul depasirii de panta valoarea medie a semnalului y(t) este o dreapta (dreapta intre Asi B).
Scriu ecuatia unei drepte care trece printr-un punct de coordonate cunoscute si de panta data y(t) - y(tA) = -x(t-ta)
![]()
deci y(t)=-x(t-tA)+EscosF
Din egalitatea ![]() rezulta:
rezulta: ![]() , deci
, deci
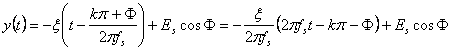
Similar pentru dreapta CD se obtine relatia:
![]()
In consecinta, cand coderul este in depasire indiferent de sensul depasirii avem relatia:
![]()
cu conditia ![]() , k=0,1,2,3,..
, k=0,1,2,3,..
Depasirea devine
totala cand ![]() , adica cele doua puncte B si C se suprapun;
, adica cele doua puncte B si C se suprapun;
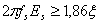
In acest caz semnalul y(t) este un semnal triunghiular cu periodicitatea semnalului de intrare
Daca ![]() pentru o portiune a perioadei smnalului x(t), atunci y(t) se
compune din segmente de dreapta racordate cu segmente de sinusoida.
pentru o portiune a perioadei smnalului x(t), atunci y(t) se
compune din segmente de dreapta racordate cu segmente de sinusoida.
Daca depasirea de panta este mare, eroarea, deci si zgomotul de depasire de panta este mare, acesta se intersecteaza in timp cu semnalul spre deosebire de zc care nu produce acest efect.
Variatia liniara
a semnalului y(t) intre punctele A-B si C-D a aparut datorita presupunerii ca
integratorul este ideal. In realitate integratorul este un circuit RC iar
semnalul y(t) pe timpul depasirii de panta are valoare medie cu variatie
exponentiala, de aici si denumirea de MDE.
In cazul acestui
integrator cu pierderi cunoscand parametrii succesiunii de impulsuri ![]() rezulta:
rezulta:
![]() , unde V0=tensiunea initiala pe capacitate. Panta
initiala a semnalului este:
, unde V0=tensiunea initiala pe capacitate. Panta
initiala a semnalului este:
![]()
deci
![]() , care arata variatia tensiunii pe capacitate in functie de
tensiunea initiala V0 si panta initiala g0.
, care arata variatia tensiunii pe capacitate in functie de
tensiunea initiala V0 si panta initiala g0.
In mod similar ca la varianta liniara a semnalului y(t), si la variatia exponentiala se poate exprima relatia lui y(t)
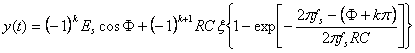 , cu conditia:
, cu conditia:
![]()
Cand coderul
este depasit total, ![]() si daca
si daca ![]() , atunci raportul pantelor celor doua semnale, se
demonstreaza
, atunci raportul pantelor celor doua semnale, se
demonstreaza
![]()
Comparandu-se raportul pantelor semnalelor de la variatia liniara cu acelasi raport de la variatia exponentiala si constatand ca au aceleasi valori, deoarece T1=RC>>Te ceea ce justifica aproximarea care se face curent in practica ca integratorul RC sa se apropie de un integrator perfect dar puterea semnalului de eroare este mai mare la varianta exponentiala.
Daca procesul de codare delta este simetric, in timpul pauzei, x(t)=0, semnalul L(t) are modelul 101010 cu frecventa fundamentala fe/2 rejectata la decoder de FTJ, deoarece fe>>f2=ft.
In practica acest proces nu este simetric si in modelul de pauza pot aparea mai multe simboluri consecutive de acelasi tip11100010010
Asimetria care genereaza asemenea modele de pauza provine din procesul cuantizarii, desi acelasi proces se poate genera daca cuantizorul este simetric dar integratorul nu este ideal.
Consideram caracteristica cuantizorului asimetric:
![]()
![]() V
V
![]() V-aV
V-aV
![]()
![]()
![]() -V
-V
-(V-aV)
![]() y(t)
y(t)
n
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 6m
6m

![]()
![]()
![]() 4m
4m![]()
![]()
![]() n-m
n-m![]()
![]()
![]()
![]()
![]()
![]() 2m
2m
![]() -(n+m)
-(n+m)![]()
![]()
![]()
![]()
![]()
![]()
![]() 0 t
0 t
![]()
![]()
![]() n-m -b
n-m -b
![]()
![]()
![]() -2m -(n+m)
-2m -(n+m)![]()
![]()
![]() -4m
-4m![]()
![]() -6sm
-6sm![]()
![]() 1 0 1 0 1 0 1 1
1 0 1 0 1 0 1 1
aV=m
In desen J=6m
Nota:
Deoarece N1=3, din desen se vede ca 6m=2mN1 si rezulta ca y(t)=-2mN1.
Nesimetria caracteristicii cuantizatorului determina ca semnalul L(t) sa fie format din impulsuri cu marimea (V-aV)t cand e(t)>0 sau -(V+aV)t cand e(t)<0. V>>aV
Treptele de la
iesirea integratorului sunt![]() si respectiv
si respectiv ![]() . S-a ales n=6m; aV=m.
. S-a ales n=6m; aV=m.
Presupunem ca la t=0; y(t)=E0=n-m atunci dupa al 3-lea impuls negativ vor trebui generate doua impulsuri pozitive, consecutive, care perturba modelul de pauza.
Deci dupa N1 impulsuri, y(t)=-2mN1 si impulsul pozitiv urmator face ca y(t) sa creasca de la -2mN1 la -2mN1+(n-m)=-b, acum se produce al doilea impuls poyitiv consecutiv.
Valoarea lui b depinde de marimea asimetricii.
Daca b este numar rational intreg sau fractional, pozitiv sau negativ, semnalul y(t) este periodic cu frecventa fundamentala determinata de (n-m)/(2m) si de frecventa de tact fe.
In figura de mai jos sunt prezentate doua forme caracteristice ale semnalului din care se observa ca y(t) poate fi considerat ca suma a doua semnale:
unul dinte de fierastrau cu frecventa fy
si
semnalul de panta ideal cu fp=fe/2
Cateva tipuri de semnale caracteristice:
![]()
![]() 1/fy
1/fy
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() t
t
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
1/fy
![]()
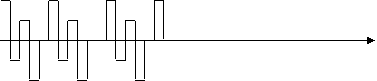
Zgomotul de pauza este tocmai semnalul in dinte de fierastrau care are fundamentala:
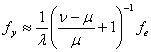 ,
,
unde l=numarul varfurilor pozitive intr-o perioada a semnalului de iesire.
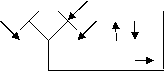
In general Zp se poate reduce prin plasarea unui circuit ca in figura de mai jos, intre iesirea lui L(t) si intrarea integratorului, ceea ce determina ca marimea impulsului + si - aplicat la integrator sa fie identic.
![]()
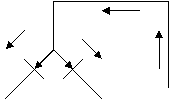
![]()
LVC
![]()
![]()
![]()
![]()
![]()
![]() L(t)
L(t)
![]()
![]()
![]()
![]() la
integrator
la
integrator
unde LVC = limitatorul variatiilor de curent
3.1. Modele de calcul
Calculul functiei de densitate spectrala a ereorii in m.d.s.i. este dificil din cauza buclei de reactie . Acest calcul se poate simplifica daca m.d.s.i. este reprezentat exact de un model in bucla deschisa .
Pentru cazul cand coderul nu este depasit exista doua modele de reprezentare .
modelul de modulatie discreta a fazei impulsurilor
modelul in scara infinita
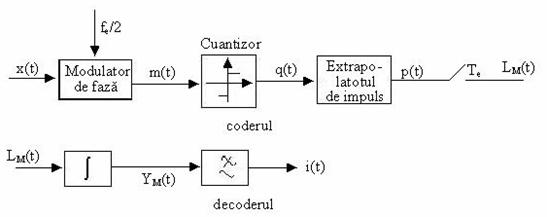
FIGURA 7.11-modulatia discreta a fazei impulsurilor
Semnalul analogic x(t) moduleaza o purtatoare sinusoidala cu frecventa fe/2 ; fe = frecventa de esantionare de la m.d.s.i.Deviatia maxima a frecventei purtatoare este de la 0 la fe .
Pentru a constata daca modelul este identic cu cel al m.d.s.i. , vom analiza comportarea schemei cu si fara semnal .
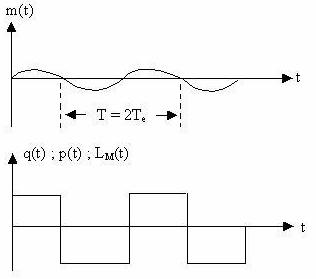
FIGURA 7.12-analiza semnalului
Cand x(t) = 0
se observa ca :
LM (t) = L(t) pentru m.d.s.i.
Deci semnalul de pauza al modelului coincide cu semnalul de pauza al m.d.s.i.
Cand
![]() , la iesirea modulatorului se obtine
, la iesirea modulatorului se obtine
![]() , in care valoarea instantanee a unghiului de faza este
proportionala liniar cu semnalul de intrare adica
, in care valoarea instantanee a unghiului de faza este
proportionala liniar cu semnalul de intrare adica ![]()
Kd
Daca frecventa modulatoare a lui
m(t) este fi , adica ![]()
prin derivare va rezulta ![]()
![]()
Pentru a nu se
produce supramodulatie ![]() nu trebuie sa depaseasca valoarea
nu trebuie sa depaseasca valoarea ![]() .
.
Deci ![]() ;
; ![]() ;
; ![]()
Deci relatia lui m(t) devine :
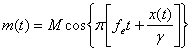
Notam cu R numarul de rotatii complete , pozitive de faza a lui m(t) ;
![]() si notam cu
si notam cu ![]() excesul de faza ;
excesul de faza ; ![]()
Atunci pentru un moment t faza
semnalului m(t) se poate pune sub forma : 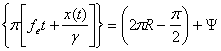
Atunci prima
trecere pozitiva prin zero apare cand faza lui ![]() , adica cand
, adica cand ![]() si
si ![]() , iar urmatoarele cand
, iar urmatoarele cand
![]() si
si ![]()
Adica cand
faza lui m(t) este : ![]() ;
; ![]() ;
; ![]() ; .
; .
Presupunem ca la un moment t au
aparut N perioade de esaantionare , adica ![]() ; atunci relatia de
mai sus devine :
; atunci relatia de
mai sus devine :
![]() *
*
M.D.S.I. are
un model de repaus simetric .101010.,adica ![]() , care poate fi
conditie initiala pentru N=1 si
, care poate fi
conditie initiala pentru N=1 si ![]()
Atunci dupa timpul t=N/fe
vom avea : ![]()
iar N = Np+Nn , Np=impulsul pozitiv , Nn=impulsul negativ
![]()
In model pentru fiecare rotatie a unghiului de faza R apare un impuls pozitiv , adica R=Np deoarece nu avem D.P. ,deci relatia * devine
![]() sau
sau ![]()
deci ![]()
In aceasta relatie se observa aparitia erorii intre semnalul de la in-
trare si cel de la iesire :
![]()
Cand ![]()
![]()
![]()
Aceasta
eroare arata ca iesirea yM(t) , a modelului difera de intrarea x(t)
printr-un modul care nu depaseste marimea ![]() a treptei de
cuantizare . Deci modelul este identic cu M.D.S.I.
a treptei de
cuantizare . Deci modelul este identic cu M.D.S.I.
3.3. Modelul in scara infinita (m.s.i.)
Este un model mai simplu ca cel
anterior , precis si general . Modelul in scara infinita se bazeaza pe
observatia ca semnalul de reactie y(t) din decoderul local al m.d.s.i. se poate
obtine din 2 functii in scara infinita cu trepte uniforme de marime ![]() si durata
si durata ![]() , una pentru momentele
pare de esantionare yp(t) si una pentru momentele impare de
esantionare
, una pentru momentele
pare de esantionare yp(t) si una pentru momentele impare de
esantionare
Yi(t)
, decalate in ambele coordonate cu ![]()
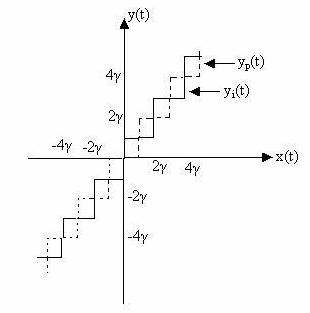
FIGURA 7.13-modelul in scara infinita
Rezulta ca schema m.s.i. este formata din :
2 cuantizori Qi si Qp care formeaza cele 2 functii in scara yi(t) , respectiv yp(t)
2 comutatoare de esantionare Si si Sp pentru esantionarea la momente impare si pare de timp cu frecventa fe/2 ;
furnizand ![]() si respective
si respective ![]() ;
;
1 dispozitiv de sumare care formeaza functia : ![]()
cu frecventa fe
1 circuit de extrapolare de ordinul zero care pastreaza fiecare impuls pe durata 1/fe
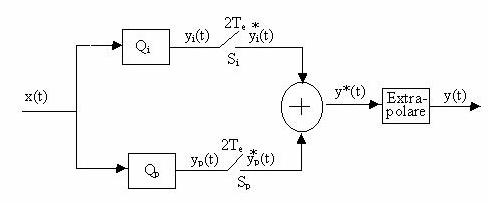
FIGURA 7.14-schema m.s.i.
In acest fel semnalul y(t) de la m.s.i. este identic cu y(t)de la m.d.s.i.
Vom face analiza teoretica a zgomotului de cuantizare prin metoda spectrului normal, care are avantajul ca rezultatele se interpreteaza grafic usor. Aceasta determinare se face pentru MDSI in urmatoarele ipoteze:
modelul de analiza este cel in scara infinita
coderul nu intra in depasire de panta
semnalul de intrare il constituie zgomotul alb banda limitata.
Pentru a ne asigura ca nu se produce depasirea de panta se pune conditia ca valoarea medie patratica a pantei semnalului de intrare sa fie cel mult egala cu ¼ din panta semnalului y(t).
Se stie conditia generala de la MDSI ca :
![]() .
.
Daca x(t) este semnal gaussian cu banda limitata intre 0 si f2 Hz si are valoarea medie pataratica σ2, atunci valoarea medie patratica a acestui semnal este:
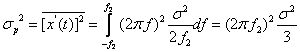 ,
,
unde ![]() este functia de
densitate spectrala iar (2πf)2 reprezinta functia de transfere
in putere a diferentiatorului.
este functia de
densitate spectrala iar (2πf)2 reprezinta functia de transfere
in putere a diferentiatorului.
Daca ![]() , rezulta ca :
, rezulta ca :
![]() .
.
Daca banda semnalului este limitata de f1 si f2,
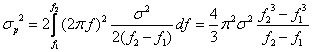 ,
,
iar dupa
conditia ![]() rezulta:
rezulta:
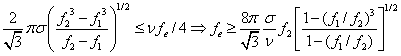 .
.
Cu precizarile de mai sus se poate opera cu modelul in scara infinita.
Algoritmul pentru determinarea Zc are trei etape:
determinarea functiei de autocorelatie la iesirea modelului cu ajutorul spectrului normal
aplicarea transformatei Fourier functiei de autocorelatie pentru a se obtine functia de densitate spectrala
descompunerea functiei de densitate spectrala in componente semnificative si interpretarea acestora.
3.4. Calculul zgomotului de cuantizare cu modelul in scara infinita
Se aplica la calcularea spectrului distorsiunilor in sistemele neliniare (MIC si MD). Ofera o analiza profunda a sistemului analizat .
Se stie ca modelul in scara infinita are 2 elemente neliniare Qp si Qi.
Initial vom considera un element neliniar caruia ii aplicam semnal Gaussian cu medie nula, adica semnal normal, care este caracterizat de urmatoarele propritati statistice:
f(x) - densitate de probabilitate a amplitudinilor (Gaussiana);
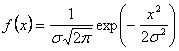
valoarea mediei = 0;
σ2 - dispersia;
ρx(τ) - coeficientul de autocorelatie;
Φx(f) - densitatea spectrala normata:
Rx(τ)=σ2ρx(τ) - functia de autocorelatie;
Sx(f)=σ2Φx(f) - densitatea spectrala.
Daca consideram un element neliniar cu caracteristica de mai jos:
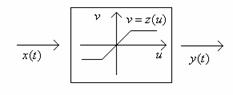
Semnalul de la iesire se poate pune sub forma:
![]()
unde Hn sunt functii de baza de tipul polinoamelor Hermite iar τn coeficientii lor.
Relatia de mai sus este valabila daca Hn sunt functii exponentiale reciproc ortogonale. Mai cunoscute sunt 3 functii de baza: functiile Hermite, Rademacher si Walsh.
Pentru simplificarea notatiilor
vom nota ![]() , deci
, deci
![]() .
.
Deoarece functiile de baza Hn(x) sunt ortogonale pe un interval de timp dat se poate evoca proprietatea de finalitate a coeficientilor; adica se pune in evidenta faptul ca suma converge rapid, iar limita nu trebuie dusa la ∞ ci la N, peste care contributia celorlalti termeni (n>N) este nesemnificativa. Deci vom avea:
![]()
![]()
Polinoamele Hermite se definesc astfel:
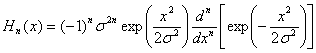
Primii 6 termeni sunt:
H0(x)=1; H1(x)=x; H2(x)=x2-σ2; H3(x)=x2-3σ2x; H4(x)=x4-6σ2x2-3σ4;
H5(x)=x5-10σ2x3+15σ4x.
Retinem doua proprietatii ale polinoamelor Hermite:
proprietatea de ortogonalitate
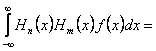
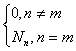
unde 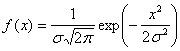 si
si 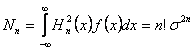
proprietatea de paritate - imparitate (Hn(x) este para pentru n par si impara pentru n impar).
Notam pentru momentul t1: x(t)=x(t1); z(x)=z(x1)
pentru momentul t2=t1+τ: x(t)=x(t2); z(x)=z(x2).
Atunci functia de autocorelatie a semnalului de la iesirea elementului neliniar considerat este:
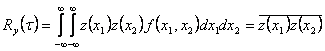 - valoarea medie
(asteptata)
- valoarea medie
(asteptata)
unde f(x1,x2) este densitatea de probabilitate de ordin 2 si are relatia:
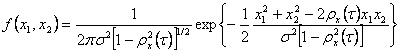
Aceasta expresie se poate simplifica cu ajutorul formulei lui Mehler:
![]()
Comsiderand
ca ![]() si
si ![]() relatia lui Ry(τ)
devine:
relatia lui Ry(τ)
devine:
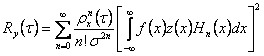
notam 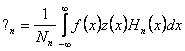 se obtine
se obtine ![]() .
.
Daca se compara
prima si ultima forma de scriere a lui ![]() se constata ca
integrala dubla si functia de densitate de probabilitate de ordin 2 au fost
inlocuite cu o serie de puteri. Coeficientii acestei serii de puteri sunt ?n
si depind de polii H, de neliniaritatea functiei z(x), de functia de
densitate de probabilitate f(x) si de puterea semnalului de intrare prin Nn
si nu depinde de forma functiei de densitate spectrala Φx(f) a
semnalului de intrare. Deci, desi metoda spectrului normal este limitata la
semnalele Gaussiene, forma spectrului lor este arbitrara.
se constata ca
integrala dubla si functia de densitate de probabilitate de ordin 2 au fost
inlocuite cu o serie de puteri. Coeficientii acestei serii de puteri sunt ?n
si depind de polii H, de neliniaritatea functiei z(x), de functia de
densitate de probabilitate f(x) si de puterea semnalului de intrare prin Nn
si nu depinde de forma functiei de densitate spectrala Φx(f) a
semnalului de intrare. Deci, desi metoda spectrului normal este limitata la
semnalele Gaussiene, forma spectrului lor este arbitrara.
Functia de
densitate spectrala a semnalului y(x) de la intrarea elementului neliniar se
gaseste luandu-se transformata Fourier a functiei de autocorelatie ![]() . Deci:
. Deci:
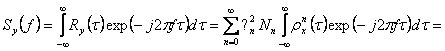
![]()
![]()
unde 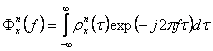 .
.
Daca n=1 se obtine transformata Fourier a coeficientului de autocorelatie .
Daca
n=2, ![]() - reprezinta
autoconvolutia functiei Φx(f), adica:
- reprezinta
autoconvolutia functiei Φx(f), adica:
![]() .
.
Similar
pentru n=3 se obtine autoconvolutia de ordinul 2 a functiei Φx(f),
adica ![]() .
.
Deci
pentru determinarea functiei de densitate spectrala Sy(f) trebuie sa
se determine mai intai autoconvolutia de ordinul n-1, adica ![]() , dar o vom numi autoconvolutie de ordin n. Initial vom
determina autoconvolutia de ordinul n pentru cazul cand x(t) este zgomot alb
filtrat trece-jos.
, dar o vom numi autoconvolutie de ordin n. Initial vom
determina autoconvolutia de ordinul n pentru cazul cand x(t) este zgomot alb
filtrat trece-jos.
Notam densitatea spectrala a semnalului x(t), pentru acest caz, cu λx(f)
![]()
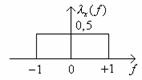
Aceasta alegere a lui λx(f) s-a facut din considerentul ca x(t) sa dea o putere de 1W pe o rezistenta de 1Ω.
Autoconvolutia lui λx(f) o notam cu ρx(τ). Atunci, cunoscandu-se λx(f) se obtine:
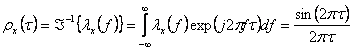 , deoarece
, deoarece ![]() .
.
Deoarece convolutiei in domeniul frecventa ii corespunde multiplicare in domeniul timp, atunci autoconvolutia de ordinul n este:
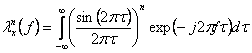
Dar
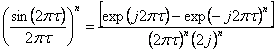 ,
, 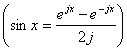
si aplicand dezvoltarea prin
teorema binomiala, ![]() ;
; ![]() , rezulta ca:
, rezulta ca:
![]()
![]() .
.
Deci
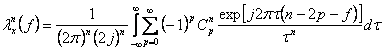 .
.
Notam
![]() si
si 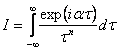 .
.
Integrala
I o putem exprima in functie de variabila z a planului complex: 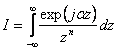 .
.
Integrandu-se pe contur se constata ca I are aceiasi valoare in modul atat pentru α>0, cat si pentru α<0, iar semnul este determinat de α, deci:
![]()
Rezulta ca:
![]()
dar ![]()
![]()
Deci: ![]()
![]()
Pentru n=2 se obtine prima autoconvolutie a lui λx(f):
![]()
In functie de valorile lui f se obtine:
|
f |
..-3 -2 -1 0 1 2 3 |
|
λx2(f) |
0 0 0 |
( Obs.: C02=1,C12=2,C22=1,Cmn=![]() )
)
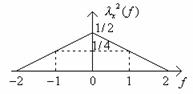
Pentru orice
valoare a lui n valorile functiei λxn(f) se obtin cu
relatia de mai sus. Totusi, cand n devine foarte mare calculele se complica si
din fericire curba triunghiulara pentru cazul n=2 tinde catre o curba
Gaussiana; relatia lui λxn(f) pentru ![]() devine:
devine: 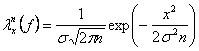 , de unde se observa ca dispersia curbei λxn(f)
este σ2n.
, de unde se observa ca dispersia curbei λxn(f)
este σ2n.
Folosindu-se rezultatele de la determinarea autoconvolutiei de ordin n a zgomotului alb filtrat trece-jos se va estima autoconvolutia de ordinul n a zgomotului alb filtrat trece banda care conduce la obtinerea puterii de 1W pe 1Ω.
Functia de densitate spectrala de putere a semnalului x(t) este Φx(f) si are reprezentarea grafica de mai jos:
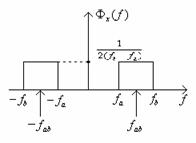
adica ![]() , unde
, unde ![]() ;
; ![]() .
.
Autoconvolutia functiei Φx(f) este:
![]()
![]()
![]()
![]()
unde λx2(f)
este autoconvolutia lui λx(f) data de relatia de zgomot alb
filtrat trece-jos pentru n=2, iar parametrii ![]() si
si ![]() reprezinta λx2(f)
deplasat in frecventa cu 2fab si respectiv -2fab.
reprezinta λx2(f)
deplasat in frecventa cu 2fab si respectiv -2fab.
Astfel
![]() .
.
Coeficientii termenilor λx2() sunt dati de coeficientii binomiali definiti prin Cpn.
Autoconvolutia de ordin doi este:
![]() .
.
Pentru autoconvolutia de ordin n-1 se obtine expresia generala:
![]()
Reprezentarea grafica a acestor functii este facuta mai jos:
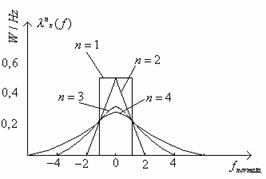
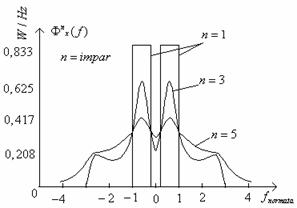
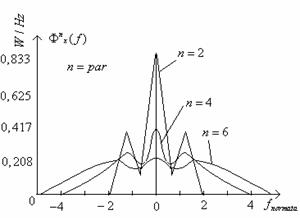
Deoarece in schema modelului in scara infinita, dupa elementul neliniar urmeaza circuitul de esantionare trebuie luat in considerare efectul acestuia asupra functiilor de autocorelatie si implicit asupra functiilor de densitate spectrala.
Se va demonstra faptul ca functia de autocorelatie esantionata este egala, la momentele de esantionare, cu functia de autocorelatie multiplicata prin frecventa de tact. Nu se impusese nici o restrictie asupra frecventei de esantionare, adica fe><fN, deci R*(nTe)=feR(nTe).
Demonstrarea acestei relatii este urmatoarea:
Consideram un semnal z(t) care este
esantionat cu o succesiune de impulsuri ![]() pentru a da un set de
impulsuri z*(t).
pentru a da un set de
impulsuri z*(t).
Atunci ![]() , unde
, unde ![]() .
.
Daca se ia transformata
Fourier a lui ![]() se obtine:
se obtine:
![]()
Spectrul undei esantionate z*(t) este obtinut prin convolutia lui z(t), adica a lui z(j2πf) cu spectul secventei de impulsuri.
![]() ,
,
deci ![]() .
.
Functia de densitate spectrala a lui z*(t) este :
![]() , c - complex conjugat,
, c - complex conjugat,
adica ![]() .
.
Se observa ca functia Sz*(f) se compune din spectrele Sz(f) distantate la fe Hz si normate in amplitudine prin fe2.
Reprezentarea grafica este urmatoarea:
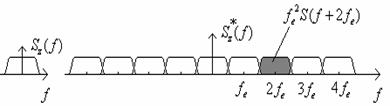
Datorita periodicitatii
lui Sz*(f), functia de autocorelatie esantionata pe
intervalul ![]() este
este 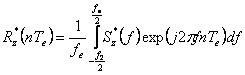 .
.
Pentru generalizare se extind limitele de integrare in gama frecventelor (2k-1)fe.
Introducand si valoare lui Sz*(f) se obtine:
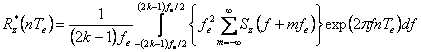 .
.
La limita vom obtine:
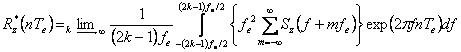 .
.
Notam 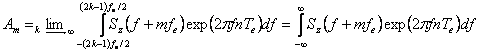 .
.
Observand ca Sz(f+mfe)
este spectrul Sz(f) plasat la mfe, relatia lui Am
se mai poate scrie ca: 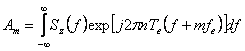 .
.
Deoarece ![]() , rezulta ca
, rezulta ca ![]() deoarece n si m sunt
valori intregi.
deoarece n si m sunt
valori intregi.
In consecinta : 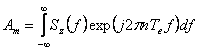 , si revenind la relatia Rz*(nTe)
se obtine :
, si revenind la relatia Rz*(nTe)
se obtine : ![]() .
.
Daca functia de
autocorelatie a semnalului z(t) inainte de esantionare este Rz(θ),
atunci 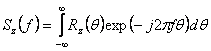 si deci :
si deci :
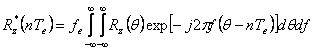 .
.
Deoarece 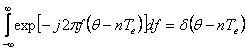 rezulta ca :
rezulta ca :
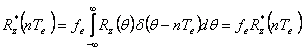 , c.c.t.d. .
, c.c.t.d. .
In continuare luam in considerare si circuitul de extrapolare, conform schemei :

Raspunsul la impulsul unitar al circuitului de extrapolare h(t) trebuie sa fie ca in figura :
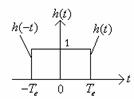
Transformata Fourier a lui h(t) este H(j2πf), iar functia de transfer in putere a circuitului de extrapolare este Sh(f).
Densitatea spectrala la iesirea circuitului de extrapolare este data de relatia : Sw(f)=Sz*(f) Sh(f).
Atunci se poate exprima autoconvolutia semnalului w(t) astfel :
![]() , unde
, unde ![]() este o functie de
timp.
este o functie de
timp.
![]() .
.
Se observa ca Rh(θ) este o functie simetrica Rh(θ)= Rh(-θ):
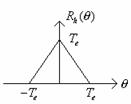
Atunci daca reprezentam functia Rh(-θ) la momentul de esantionare nTe obtinem:
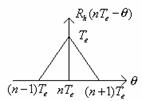
Pentru a analiza autoconvotia dintre Rh(θ) si Rz*(θ) sa-l reprezentam si pe Rz*(θ):
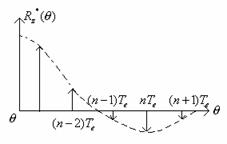
Atunci 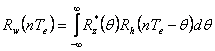 , cu precizarea ca
, cu precizarea ca 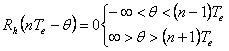
Latimea maxima a lui Rh(nTe-θ) este 2Te.
Atunci: ![]() .
.
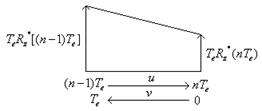
Sa analizam functia Rw(nTe) intre momentele de esantionare. Daca se face o translatie a functiei Rw(nTe-θ), (din figura anterioara) in intervalul perioadei de esantionare se observa:
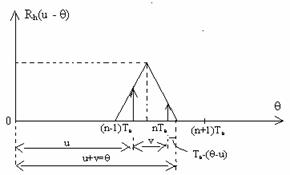
u+v=θ; din cele 2 triunghiuri dreptunghice asemenea se poate scrie:
![]() ,
,
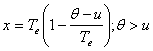 si similar
si similar 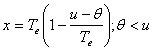 .
.
Daca le exprimam functie de variabila u-θ atunci Rh(θ) devine Rh(u-θ) care este tocmai x, deci:
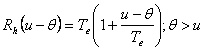 si
si 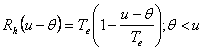 .
.
Rezultatul este evident deoarece intre momentele de esantionare Rh(θ) nu poate fi mai mare ca Te.
Deoarece relatiile de mai sus se pot exprima si functie de variabila v care este θ - u se obtine:
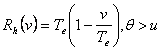 si
si 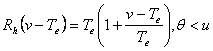 .
.
Acum se poate exprima Rw(u-θ):
![]() .
.
Inlocuindu-se expresiile lui Rh(v) si Rh(v-Te) se obtine:
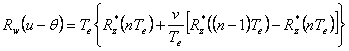 .
.
Sintetizand rezultatele efectului de extrapolare, reprezantate in figura de mai jos, se poate concluziona ca desi functia de autocorelatie a semnalului la iesirea circuitului de extrapolare, Rw(θ), este egala cu esantioanele lui Rz(θ) normate prin Te la momentele de esantionare, aceasta functie nu este o curba neteda, ci din segmente de dreapta corespunzatoare perioadei de esantionare.
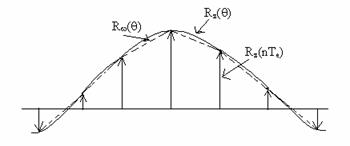
Deci Rw(θ) este o buna aproximare a lui Rz(θ).
Pentru modelul in scara infinita vom determina initial functia de autocorelatie a semnalului y*(t). La semnalul din schema modelului sosesc pe cele 2 cai esantioanele pare si impare. Consideram o succesiune de esantioane:
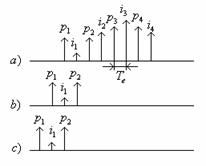
Functia de autocorelatie a semnalului y*(t), notata prin R*(θ) se determina multiplicarea succesiunii a) de esantioane cu ea insasi. Deci:
![]() .
.
Pentru a determina pe R*(Te) deplasa succesiunea a) cu Te, obtinand pe b) si inmultim cu a).
![]() .
.
Daca se mai face o deplasare cu Te se obtine:
![]()
![]() .
.
Se observa relatiile generale pentru momentele pare si impare de timp:
![]() , respectiv
, respectiv ![]() .
.
Sumand
aceste doua relatii se obtine: ![]() .
.
Densitatea spectrala se obtine prin aplicarea transformatei Fourier:
![]() ;
; ![]() ;
;
![]() .
.
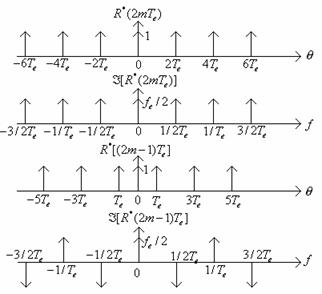
Am
vazut anterior ca spectrul unui semnal esantionat cu functia delta-periodica
este de forma: ![]() .
.
Tinand cont de aceasta precizare, ultima relatie se poate scrie:
![]() .
.
Daca
mai tinem cont si de relatia: ![]() , atunci, pentru decoderul local al MDSI, putem exprima functia de densitate spectrala
esantionata:
, atunci, pentru decoderul local al MDSI, putem exprima functia de densitate spectrala
esantionata:
![]() .
.
Observand ca:![]() , rezulta:
, rezulta:![]()
Aceasta relatie se poate exprima sub forma a doua componente, para si impara, conform relatiei generale prezentate anterior. Astfel:
- Pentru momentele pare de esantionare:
![]()
Daca corelam aceasta exprimare cu cea anterioara putem observa ca se mai poate scrie:
![]() ,
,
in care l1,p si l2,p sunt coeficientii definiti anterior si particularizati pentru functiile in scara infinita yp si yi conform lui zp(x) si zi(x).
In
relatia de mai sus ![]() .
.
- Pentru momentele de esantionare impare rezulta in mod similar:
![]() .
.
Pentru evaluarea relatiilor lui Si*(f) trebuie sa determinam functia de autocorelatie intretesuta Rpi[(2m-1)Te].
Considerand
cazul general a doua functii A(t) si B(t) neliniare care prin intretesere
compun functia C(t). Cele doua functii presupuse le exprimam prin polinoame
Hermit, ca asa am convenit la tehnica spectrului normat: ![]() , respectiv
, respectiv ![]() .
.
Atunci functia de corelatie intretesuta :
![]() .
.
Conform proprietatii de ortogonalitate a functiilor Hermite avem:
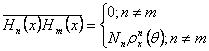 , unde Nn si ρxn(θ)
au fost definite anterior.
, unde Nn si ρxn(θ)
au fost definite anterior.
Deci
![]() .
.
Functia de densitate spectrala intretesuta:
![]() .
.
Aplicand acest rezultat lui Si*(f) se obtine:
![]() .
.
Daca sumam Sp*(f) cu Si*(f) se obtine Sy*(f):
(1) ![]()
![]() .
.
Aceasta relatie se poate simplifica daca consideram valorile intregi pare si impare ale lui m in intervalul −∞ +∞.
Pentru cazul par, m=2k, si impar, m=2k−1:
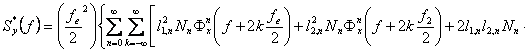
![]()
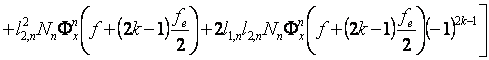
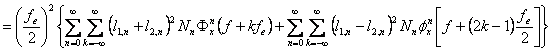
In aceasta relatie observam ca:
![]() si
si 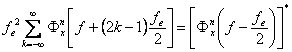
Atunci:
(2) 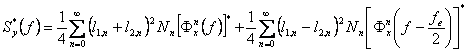 .
.
Deci functia de densitate spectrala la momentele de esantionare, Sy2(f), a semnalului de reactie din coderul delta se poate exprima prin cele doua relatii (1) si (2).
In relatia (1) functia Sy2(f) a fost stabilita prin esantionarea la jumatate din frecventa de tact la momentele de esantionare pare si impare rezultand spectrul localizat la multiplii jumatatii frecventei de esantionare.
Relatia (2) arata ca spectrul este
localizat la multiplii frecventei de esantionare deoarece ![]() este identic cu
este identic cu 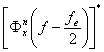 , cu exceptia unei deplasari de frecventa de fe/2.
Deci este mai avantajos sa lucram cu relatia (2).
, cu exceptia unei deplasari de frecventa de fe/2.
Deci este mai avantajos sa lucram cu relatia (2).
Semnalul y(t) de la ieserea integratorului din bucla de reactie a MDSI este identic cu semnalul de la intrarea circuitului de extrapolare din modelul in scara infinita.
Deci functia de densitate spectrala
a semnalului y(t) devine ![]() ,
,
unde
![]() functia de densitate
spectrala a circuitului de extrapolare.
functia de densitate
spectrala a circuitului de extrapolare.
Acum
putem determina puterea de la iesirea integratorului in banda mesajului: 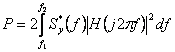 (2-ul din fata integralei apare de la functia de densitate spectrala
a zgomotului alb filtrat trece banda;
(2-ul din fata integralei apare de la functia de densitate spectrala
a zgomotului alb filtrat trece banda;
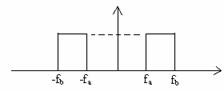
iar ![]() ).
).
In expresia puterii scisa mai sus este cuprinsa atat puterea semnalului cat si puterea zgomotului.
Pentru a pune in evidenta, in relatia puterii, puterea zgomotului de cuantizare in modelul in scara infinita exprimam diferenta dintre semnalul la iesirea functiilor in scara infinita si semnalul de la intrare la momentele pare si impare de esantionare, astfel:
![]() , respectiv
, respectiv ![]() .
.
Semnalele Δyp si Δyi pot fi considerate ca apar la iesirea funtiilor "in dinte de fierastrau" infinite.
Pentru aceste functii coeficientii spectrali ln,p si ln,i se pot determina cu relatia lui ln inlocuindu-se z(x) cu zp(x)-x pentru momentele de iesire pare si zi(x)-x pentru cele impare, deci:
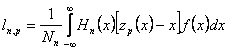 si
si 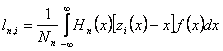 .
.
Se observa ca ![]() si
si ![]() .
.
Examimand coeficientii lx,n pentru diverse valori ale lui n, stiind expresiile polinoamelor Hermite, se obtine:
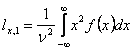
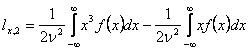
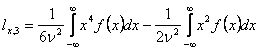
.
Se stie ca 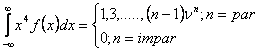 .
.
In consecinta termenii lx,n se simplifica lx,1=1; lx,n=0 pentru n≥2.
Atunci coeficientii ln,p si ln,i devin:
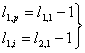 pentru n=1
pentru n=1
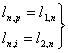 pentru n≥2.
pentru n≥2.
Se observa ca pentru n≥2 coeficientii functiei "in dinte de fierastrau" sunt identici cu coeficientii functiei in scara si coeficientii de ordinul unu ai functiei "in dinte de fierestrau" sunt egali cu cei ai functiei in scara din care se scade 1.
De la functiile neliniare impare stim z(x)=−z(−x), atunci coeficientii
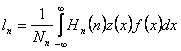 sunt nuli cand n=par.
sunt nuli cand n=par.
Aceasta afirmatie se verifica daca
in expresia lui ln se divide intervalul de integrare: 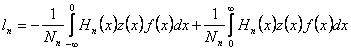 , deci vom avea numai coeficientii de ordin impar.
, deci vom avea numai coeficientii de ordin impar.
Cu aceste precizari relatia (2) a densitatii spectrale devine:
![]()
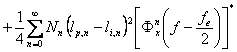
Inlocuind ![]() , rezulta:
, rezulta:
(3)
![]()
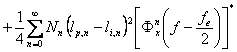 .
.
Relatia (3) a densitatii spectrale are trei termeni:
primul termen este proportional cu densitatea spectrala de intrare
ceilalti doi corespund efectelor cuantizarii.
Daca facem notarile:
![]() - factor de amplificare prin coder care are
o
- factor de amplificare prin coder care are
o
valoare apropiata de 1.
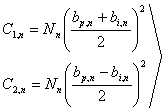 - coeficienti spectrali ai distorsiunii de cuantizare,
- coeficienti spectrali ai distorsiunii de cuantizare,
relatia (3) devine: (4)  .
.
In relatia (4) termenul doi reprezinta spectrul distorsiunii care apare pe armonicele frecventei de esantionare, se mai numeste spectrul centrat SCEN*(f), iar al treilea reprezinta spectrul care apare la armonicele frecventei fe/2 - spectru descentrat - SDES*(f).
Deci spectrul zgomotului de cuantizare:
![]() si
si ![]() .
.
Revenind la relatia puterii putem scrie:
(5) 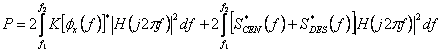
![]() .
.
Stiind ca ![]() , se observa ca pentru m≠0 spectrele cad inafara benzii
de trecere f1f2, deci:
, se observa ca pentru m≠0 spectrele cad inafara benzii
de trecere f1f2, deci: ![]() ; f1<f<f2.
; f1<f<f2.
Acum putem exprima raportul S/Zc.
Mai intalnite sunt doua moduri de definire a S/Zc:
ca raport intre puterea semnalului de intrare si
puterea zgomotului la iesire in prezenta semnalului, adica ![]() ;
;
ca raport intre puterea semnalului in prezenta
zgomotului la iesire si puterea zgomotului la iesire in prezenta semnalului,
adica ![]() .
.
Daca K din relatia (5) il aproximeaza pe ν2 cele doua expresii sunt echivalente.
Cu precizarile de mai sus din relatia (4) separam spectrul zgomotului de cuantizare:
![]() .
.
Tinand cont de functia de transfer a circuitului de extrapolare se obtine relatia finala a densitatii spectrale a zgomotului de cuantizare:
(6) ![]() .
.
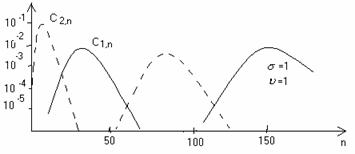
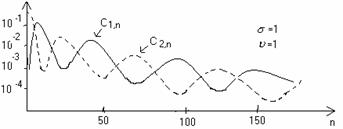
Din reprezentarea grafica a coeficientilor spectrali C1,n si C2,n se observa urmatoarele:
prin cresterea lui n coeficientii Cn prezinta maxime si minime, iar valoarea medie a acestora scade;
prin micsorarea marimii treptei de cuantizare creste diferenta dintre maximele si minimele adiacente coeficientilor Cn precum si intervalul dintre varfurile adiacente, deasemenea creste valoarea medie;
C2,n are maximum inaintea lui C1,n;
pentru n≤25 semnificativi sunt coeficientii C2,n, iar spectrul distorsiunii depinde de spectrul descendent si deoarece SDES(f) scade cu f, in banda mesajului valoarea a este mica.
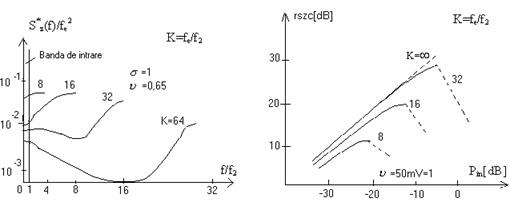
Referitor la influenta frecventei de esantionare se observa ca:
reducerea zgomotului se face prin cresterea lui fe care nu afecteaza forma spectrelor SCEN siSDES ci numai localizarea lor;
deoarece SCEN siSDES depind de marimea ν si banda semnalului de intrare, rezulta ca si valoarea fe peste care nu se mai produce nici o imbunatatire depinde si ea de acesti parametrii.
Rszc
pentru fe>32f2 rszc nu mai creste deoarece SCEN siSDES sunt efectiv separate;
partea punctata a curbelor reprezinta zgomotul.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1421
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved