APARATE SI METODE PENTRU MASURAREA IMPEDANTELOR

APARATE SI METODE PENTRU

MASURAREA IMPEDANTELOR

A. Generalitati

Impedanta este o marime care caracterizeaza functionarea elementelor de circuit in curent alternativ . Ea se defineste cu ajutorul legii lui Ohm aplicate in curent alternativ. In curent continuu , conform legii lui Ohm :

In curent alternativ , legea lui Ohm devine :

(10.2)

Avand aceeasi relatie de definitie , rezistenta si impedanta vor avea aceeasi unitate de masura , ohmul ( 1Ω = ) .

Fata de rezistenta , impedanta are un caracter mai complex deoarece in curent alternativ elementele de circuit prezinta , pe langa proprietatea de rezistenta , si proprietatile de inductanta ( L ) si capacitate ( C ) .

Inductanta este proprietatea elementelor de circuit de a se opune variatiilor de curent . Inductanta se poate defini ca raportul intre fluxul magnetic ce trece printr-un element de circuit si intensitatea curentului care a generat acel flux : .

Unitatea de masura pentru inductanta este henry ( 1H = ) . In practica se utilizeaza frecvent submultiplii mH si μH .

Inductanta este o proprietate specifica bobinelor ( inductanta proprie - a unei bobine sau inductanta mutuala - intre doua bobine , atunci cand fluxul creat de bobina trece si prin spirele celeilalte bobine ) .

Capacitatea este proprietatea elementelor de circuit de a acumula sarcini electrice si se poate defini cu raportul intre cantitatea de electricitate ce se acumuleaza intr-un element de circuit si tensiunea la care este alimentat elementul respectiv : C = .

Unitatea de masura pentru capacitate este faradul ( 1 F = ) . In practica se utilizeaza submultiplii pF , nF , si μF .

Reactanta . Valorile inductantelor si capacitatilor depind de datele constructive ale elementelor de circuit ( dimensiuni , materiale ) . In circuit , ele se manifesta prin " reactantele " corespunzatoare care depind de frecventa . In curent alternativ sinusoidal reactanta inductiva este , iar reactanta capacitiva este , unde reprezinta pulsatia .

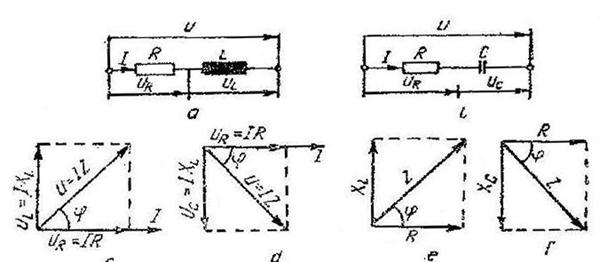
Diagrame fazoriale . Impedantele prezinta urmatoarele componente :

R - rezistenta ;

- reactanta inductiva ;

- reactanta capacitiva ;

Cele trei componente ale impedantei nu se pot insuma algebric , ci numai fazorial , deoarece inductantele defazeaza tensiunea inaintea curentului cu rad , capacitatile defazeaza tensiunea in urma curentului cu rad , iar rezistentele nu introduc nici un defazaj .

In figurile 10.1 c , si 10.1 d s-au reprezentat diagramele fazoriale corespunzatoare tensiunilor ce intervin in cazul impedantelor din figurile 10.1 a si 10.1 b . Daca in diagramele fazoriale din figurile 10.1 c si 10.1 d se simplifica toate tensiunile cu I , se obtin diagramele din figurile 10.1 e si 10.1 f reprezentand diagramele fazoriale ale impedantelor Z . Din aceste diagrame se pot calcula modulul impedantei Z si tangenta unghiului de defazaj φ dintre tensiune si curent :

; tg φ = ; (10.3)

Exprimarea impedantelor in numere complexe . Asimiland diagramele fazoriale din figura 10.1 unui plan complex ( axa orizontala - numere reale , axa verticala - numere imaginare ), impedantele se pot exprima sub forma unor numere complexe .

Fig . 10.1 Impedante si diagramele lor fazoriale.

Pe diagrame se observa ca reactantele inductive defazeaza tensiunea inaintea curentului cu rad , deci in plan complex devine , iar reactantele capacitive defazeaza tensiunea in urma curentului cu rad , deci in plan complex devine :

-jX = -j = .

Tinand seama de aceste observatii se poate scrie :

(10.4)

Nota : In aceste expresii s-au folosit j= In loc de i= , pentru a nu se crea confuzii cu intensitatea instantanee a curentului electric , care se noteaza cu i ;

Factorul de calitate . Elementele reactive de circuit ( bobinele si condesatoarele ) prezinta , pe langa reactanta ,si o rezistenta in care se consuma energie . Cu cat pierderile de energie sunt mai mici ,cu atat calitatea elementelor reactive este mai buna . Factorul de calitate care se noteaza cu Q , se defineste prin raportul intre reactanta si rezistenta unui element de circuit sau ale unui circuit :

(10.5)

Pentru o bobina care are rezistenta R, pentru un condensator cu rezistenta de pierderi R ( considerata in serie) , , iar pentru un circuit in care pe langa rezistenta bobinei mai intervin si alte rezistente R , .

B. Metode pentru masurarea impedantelor

Deoarece , asa cum s-a aratat , rezistenta in curent continuu si impedanta in curent alternativ au aceeasi relatie de definitie , metodele utilizate pentru masurarea rezistentelor in curent continuu se pot adapta si la masurarea impedantelor in curent alternativ , cu urmatoarele observatii :

- circuitele de masurare vor fi alimentate in curent alternativ de la o sursa de frecventa f ;

aparatele de masurat folosite trebuie sa fie astfel alese incat sa functioneze la frecventa f a sursei e alimentare ;

elementele de circuit , fiind alimentate in curent alternativ , se vor comporta ca impedante ;

Pornind de la aceste considerente , s-a realizat o gama variata de aparate pentru masurarea impedantelor si a componentelor lor , utilizandu-se numeroase metode de masurare . In continuare se vor analiza cateva dintre acestea .

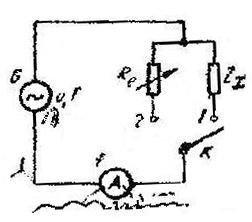
Masurarea impedantelor prin metoda substitutiei

Metoda substitutiei este cea mai simpla metoda . Ea foloseste montajul din figura 10.1 in care :

G - este un generator de c.a. de tensiune U si frecventa f ;

A - ampermetru de curent alternativ ,capabil sa functioneze la frecventa f ;

R - rezistenta variabila , etalonata ( cutie e rezistente ) ;

K - comutator cu doua pozitii ;

Modul de lucru : Acelasi ca in curent continuu , are doua etape :

I - se inchide comutatorul K pe pozitia 1 si se citeste pe ampermetrul A intensitatea I a curentului electric ( ) ;

II - se trece comutatorul K pe pozitia 2 si se regleaza rezistenta variabila , pana cand apermetrul va indica un curent I = I , rezulta ca .

Dupa cum se observa , aceasta metoda permite numai masurarea globala a impedantelor ,nu si a componentelor lor ( R , L , C ) ;

Fig .10.1 - Masurarea

impedantelor prin metoda substitutiei .

Masurarea inductantelor prin metoda apermetrului si voltmetrului

a.       Masurarea inductantelor proprii

Masurarea inductantelor proprii ale bobinelor folosind metoda apermetrului si voltmetrului se bazeaza in curent continuu si in curent alternativ .

Intrucat bobinele au de obicei impedante mult mai mici decat rezistenta voltmetrului , se foloseste varianta aval .

Montajul folosit este reprezentat in figura 10.3 . Comutatorul K , cu doua pozitii , permite alimentarea succesiva a circuitului in curent continuu si in curent alternativ .

Modul de lucru . Masurarea se desfasoara pe trei etape :

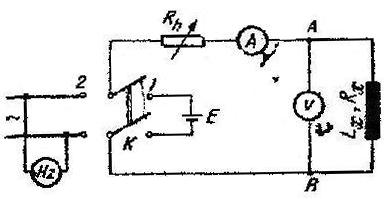
I - se inchide comutatorul K pe pozitia 1 si montajul se alimenteaza in curent continuu . Se masoara intensitatea curentului I cu ampermetrul , tensiunea U

cu voltmetrul si ,aplicand legea lui Ohm ,

se calculeaza ;

II - se trece comutatorul K pe pozitia 2 si

Montajul se alimenteaza in curent alternativ . Se masoara din nou intensitatea curentului si tensiunea si de aceasta data , aplicand legea lui Ohm, se va calcula Z . Fig . 10.3 Masurarea inductantelor     proprii prin metoda ampermetrului

si voltmetrului .

III - cunoscand valorile si Z si cunoscand sau masurand frecventa , se poate deduce valoarea inductantei :

,

de unde :

.

b.       Masurarea inductantelor mutuale

Masurarea inductantelor mutuale prin metoda ampermetrului si voltmetrului se bazeaza pe masurarea inductantei totale a doua bobine legate in serie ,in doua variante : o data astfel incat fluxurile care le strabat sa se insumeze , iar alta data astfel incat fluxurile sa se scada ( sa fie de sens contrar ) . Cum sensul fluxului depinde de sensul curentului prin bobine , este necesar ca in varianta a doua sa se inverseze sensul curentului intr-o bobina inversand legarea capetelor ei in circuit .

Masurarea inductantei totale a celor doua bobine se realizeaza cu acelasi montaj si aceeasi metoda ca si in cazul inductantelor proprii , numai ca intre punctele A , B se leaga cele doua bobine in serie .

Modul de lucru . Se procedeaza astfel :

I - cele doua bobine se leaga in serie asa incat fluxurile lor sa se insumeze ( fig. 10.4 a ) . In acest caz inductanta mutuala este pozitiva . Se masoara inductanta totala :

; (10.7)

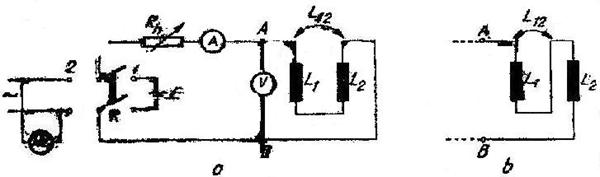
Fig. 10.4 Masurarea inductantelor mutuale .

II - cele doua bobine se leaga in serie asa incat fluxurile lor sa se scada ( fig. 10.4 b ) . In acest caz inductanta mutuala este negativa . Se masoara inductanta totala , care va fi :

. (10.8)

Facand diferenta    , se obtine :

,

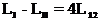de unde :

. (10.9)

Punti de curent alternativ

Puntile de curent alternativ , utilizate la masurarea impedantelor au aceeasi schema de principiu si acelasi mod de functionare ca si puntile de curent continuu . Pentru comparatie , in figura 10.5 sunt reprezentate o punte de curent continuu si o punte de curent alternativ.

Puntea de curent alternativ este alimentata de la o sursa de frecventa f , elementele din bratele sale se comporta ca impedante iar instrumentul indicator de nul trebuie sa functioneze la frecventa f a sursei .

Conditiile de echilibru . Ca si la puntile de curent continuu , cand prin diagonala in care este montat instrumentul indicator curentul este zero , intre cele doua brate ale puntii exista o relatie bine determinata, cunoscuta sub numele de conditia de echilibru , si care este aceeasi ca si la puntile de curent continuu ( produsul a doua brate opuse este egal cu produsul celorlalte doua brate opuse ,sau raportul a doua brate alaturate este egal cu raportul celorlalte doua brate alaturate ) .

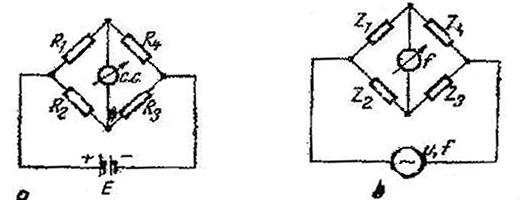
Fig. 10.5 Punti electrice de masurat :

a - punte de c.c. ; b - punte de c. a.

In curent alternativ , aceasta conditie devine :

sau . (10.10)

Fiecare impedanta poate fi exprimata prin modulul sau si prin defazajul φ pe care il introduce : . Ca urmare , conditia de echilibru se poate scrie si sub forma :

,

ceea ce este echivalent cu doua relatii : una referitoare la module si cealalta la faze :

si (10.11)

Cea de-a doua relatie arata ca puntile de curent alternativ nu pot avea orice configuratie .

Daca in doua brate alaturate ale unei punti sunt numai rezistente , in celelalte doua brate opuse trebuie sa fie reactante de semne contrare ( intr-un brat inductanta , in bratul opus capacitate ) .

De exemplu : daca si atunci si . Rezulta ca defazajele si trebuie sa fie de semne contrare , deci impedantele si sa contina reactante diferite .

Din aceasta categorie fac parte puntile Maxwell si Hay .

Daca in doua brate alaturate ale unei punti sunt numai rezistente , de exemplu si , in celelalte doua brate alaturate trebuie sa fie reactante de acelasi fel ( si deci si trebuie sa aiba acelasi semn ) . Din aceasta categorie fac parte puntile Sauty si Nernst .

Ca si la puntile de curent continuu , daca se cunosc elementele din trei brate , se pot deduce cele din al patrulea brat . Pentru calcule se utilizeaza de obicei exprimarea impedantelor sub forma numerelor complexe . In cazul cel mai general, fiecare impedanta poate fi de forma Z=R+jX si conditia de echilibru devine :

(10.12)

Desfacand parantezele si separand partea reala de cea imaginara se obtin doua relatii care exprima impreuna conditia de echilibru :

    (10.13)

Echilibrarea puntii . Pentru satisfacerea celor doua relatii de echilibru , la puntile de curent alternativ sunt necesare doua elemente de reglaj . Acestea pot fi rezistoare , bobine sau condensatoare variabile . Deoarece bobinele variabile de inductante cunoscute se realizeaza mai greu in practica , pentru echilibrarea puntilor de curent alternativ se prefera rezistoare si condensatoare variabile .

Exista o mare varietate de punti de curent alternativ . Ele poarta de obicei numele savantilor care le-au propus . Se vor analiza in continuare cateva dintre cele mai raspandite punti .

a.       Punti pentru masurarea capacitatii

Puntea Sauty ( fig. 10.6 b ) este folosita pentru masurarea condensatoarelor de buna calitate , cu pierderi mici , a caror schema echivalenta se reprezinta de obicei in figura 10.6 a . Rezistenta figurata in serie cu capacitatea reprezinta rezistenta armaturilor condensatorului si a terminalelor si este de valoare mica .

Modul de lucru . Se monteaza condensatorul de masurat la bornele special prevazute in constructia puntii si se regleaza elementele variabile pana cand instrumentul indicator arata zero . In acest moment , conditia de echilibru este satisfacuta si se poate scrie :

(10.14)

Separand partile imaginare de cele reale , rezulta :

de unde (10.15)

de unde (10.16)

Fig. 10.6 Schema echivalenta a unui condensator

cu pierderi mici . (a) ; puntea Sauty (b) .

Dupa cum se observa , este proportional cu , iar cu .

Aceasta proportionalitate permite sa se gradeze in valori ale lui si in valori ale lui . Raportul devine factor de multiplicare .

Puntea Nernst (fig. 10.7,b) se foloseste pentru masurarea condensatoarelor cu pierderi mari , a caror schema echivalenta se reprezinta de obicei ca in figura 10.7 a . Rezistenta figurata in paralel cu capacitatea este in acest caz de valoare mare si reprezinta rezistenta in curent alternativ a dielectricului dintre armaturile condensatorului . Bratul in care se afla elementele de reglaj are o schema asemanatoare cu schema echivalenta a condensatorului de masurat .

Modul de lucru . Se monteaza condensatorul de masurat la bornele prevazute in acest scop si se regleaza pe rand elementele variabile pana se aduce puntea la echilibru , cand se poate scrie :

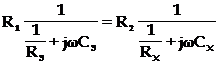(10.17)

Aducand la acelasi numitor si separand partile reale de cele imaginare , se obtine :

de unde (10.18)

de unde (10.19)

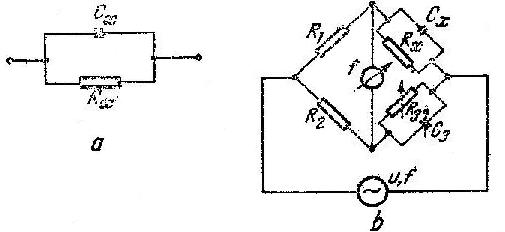
Fig . 10.7 Schema echivalenta a unui

condensator cu pierderi mari ( a ) ;

Puntea Nernst ( b ) ;

Ca si la puntea Sauty , si la puntea Nernst se pot grada in valori ale lui si in valori ale lui . Raportul devine factor de multiplicare .

Puntea Schering este una dintre cele mai raspandite punti . Este folosita atat la tensiuni joase , cat si la tensiuni inalte . De asemenea , se foloseste atat in joasa frecventa cat si la frecvente inalte .

Puntea Schering reprezentata in figura 10.8 se utilizeaza pentru masurarea condensatoarelor sub inalta tensiune . Montajul este astfel realizat incat aproape toata tensiunea sa se regaseasca la bornele condensatorelor si ; pe elementele de reglaj nu se aplica decat o mica parte din tensiunea de alimentare a puntii astfel incat sa fie respectate normele de tehnica securitatii muncii . Pentru a inlatura pericolul aparitiei unor tensiuni mari pe elementele reglabile ale puntii ,punctele A si B se conecteaza la masa prin sigurantele de protectie S . In cazul ridicarii tensiunii peste o anumita valoare , sigurantele S se strapung si bratele reglabile ale puntii sunt legate la pamant .

Modul de lucru este acelasi ca la celelalte punti . Din conditia de echilibru :

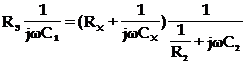(10.20)

se poate deduce :

si (10.21)

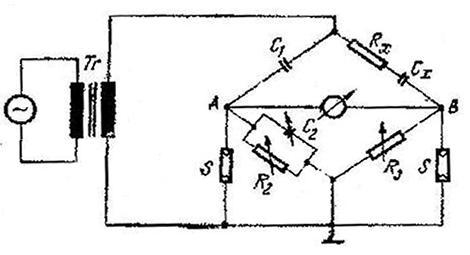
Fig. 10.8 Puntea Schering pentru masurarea

condensatoarelor sub inalta tensiune .

b.       Punti pentru masurarea inductantei

Puntea Maxwell (fig. 10.9) este cea mai utilizata punte pentru masurarea bobinelor . In constructia sa , in doua brate opuse se folosesc rezistoare, iar la bratul opus bobinei ce se masoara se afla un condensator in paralel cu un rezistor .

Modul de lucru . Se aduce puntea in echilibru prin reglarea pe rand a elementelor variabile . La echilibru se poate scrie :

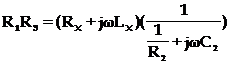(10.22)

Din relatia (10.22) se poate deduce :

si (10.23)

Puntea Maxwell este destinata masurarii bobinelor cu factor de calitate mic . La bobinele cu Q mare , este foarte mic si dupa cum rezulta din relatia (10.23) ar fi necesar ca sa fie de valoare foarte mare . Acest lucru este mai dificil de realizat in practica .

Puntea Hay (fig 10.10) se foloseste pentru masurarea bobinelor cu factor de calitate mare . Spre deosebire de Maxwell , in constructia puntii Hay elementele de reglaj din bratul opus bobinei sunt montate in serie .

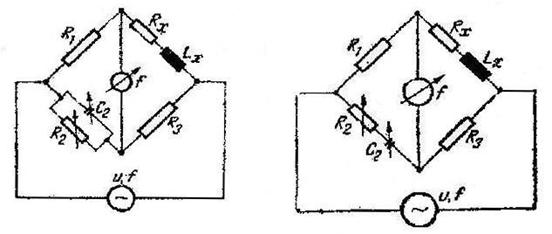
Fig. 10.9 Puntea Maxwell Fig. 10.10 Puntea Hay

Modul de lucru. Regland elementele variabile pe rand , se aduce puntea la echilibru , cand este satisfacuta relatia :

(10.24)

Separand partile reale de cele imaginare ,se obtine :

si (10.25)

Daca in ultima relatie se impart ambii termeni cu si , se observa ca :

. Rezolvand sistemul din relatiile (10.25) si tinand seama ca Q > 1 , rezulta :

si (10.26)

Dupa cum se observa din expresia lui , echilibrul acestei punti depinde de frecventa : ca urmare , tensiunea cu care se alimenteaza puntea trebuie sa fie sinusoidala, de frecventa constanta si cunoscuta .

c.        Punti RLC. Punti RC

In practica se intalnesc frecvent punti care permit masurarea rezistentelor , inductantelor si capacitatilor , cunoscute sub numele de punti universale sau punti RLC. Unele variante constructive permit numai masurarea rezistentelor si capacitatilor , fiind deci punti RC .

Aceste aparate au in componenta lor diferite elemente , care prin intermediul comutatoarelor se pot distribui astfel incat sa formeze o punte tip Wheatstone in cazul masurarii rezistentelor, de tip Sauty in cazul masurarii condensatoarelor si de tip Maxwell cand se masoara bobine .

d.       Punti electronice

In contructia puntilor moderne , intervin blocuri functionale realizate cu componente electrice . Astfel , instrumentul indicator de nul este un voltmetru electronic, pentru alimentarea in curent continuu puntile sunt prevazute cu un redresor, iar pentru masurarea in curent alternativ, la o frecventa diferita de 50 Hz, puntile sunt prevazute cu generatoare care lucreaza pe o anumita frecventa ( de obicei 1000 Hz in joasa frecventa si 1 MHz in inalta frecventa ) .

Masurari cu Q-metrul

Q-metrul este un aparat industrial destinat sa masoare factorul de calitate Q . El este un aparat foarte mult folosit deoarece permite si alte masurari , cum ar fi : masurarea inductantelor ,masurarea rezistentelor in inalta frecventa , masurarea capacitatilor etc .

Functionarea Q-metrului se bazeaza pe proprietatea circuitelor LC serie de a prezenta la rezonanta , la bornele elementelor lor , o tensiune de Q ori mai mare decat tensiunea cu care au fost alimentate in serie .

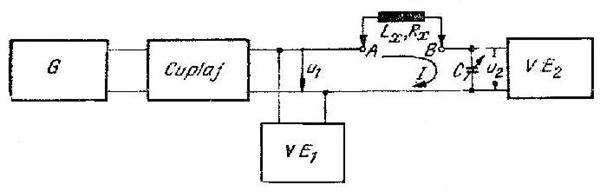
Schema de principiu a unui Q-metru este reprezentata in figura 10.11 . Condensatorul variabil C impreuna cu bobina ce se monteaza la bornele A , B formeaza un circuit LC care este alimentat in serie de la un generator G de frecventa variabila prin intermediul unui circuit de cuplaj care trebuie sa prezinte o rezistenta neglijabila . Voltmetrul electronic masoara tensiunea cu care este alimentat circuitul LC , iar voltmetrul electronic masoara tensiunea la bornele condensatorului C .

Modul de lucru . Daca circuitului LC i se aplica in serie o tensiune , intensitatea curentului prin acest circuit va fi :

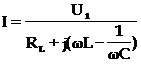(10.27)

Fig. 10.11 Q-metrul

Variind capacitatea condensatorului C sau frecventa generatorului se aduce circuitul LC la rezonanta . In acest caz , si intensitatea curentului devine maxima :

(10.28)

Rezonanta este pusa in evidenta de voltmetrul , care masoara la bornele condensatorului tot o tensiune maxima :

(10.29)

Inlocuind cu se obtine :

(10.30)

Conform relatiei (10.30) , tensiunea la bornele condensatorului C , la rezonanta , este de Q ori mai mare decat tensiunea cu care s-a alimentat circuitul .

Daca se mentine constant , .Aceasta relatie permite transcrierea scarii gradate a voltmetrului in valori ale lui Q , obtinandu-se astfel un aparat cu citire directa pentru masurarea factorului de calitate .

Punandu-se conditia , rezulta ca scara gradata in valori ale lui Q este valabila numai pentru o anumita valoare a tensiunii . Pentru a se respecta aceasta conditie , pe scara gradata a voltmetrului este trasat un reper , iar tensiunea se regleaza astfel incat indicatia voltmetrului sa fie intotdeauna la reperul respectiv .