| CATEGORII DOCUMENTE |
| Aeronautica | Comunicatii | Electronica electricitate | Merceologie | Tehnica mecanica |
Circuitele electrice de curent alternativ sunt acele circuite alimentate cu tensiuni electromotoare alternative, de obicei cu variatie sinusoidala in timp. Aceste circuite prezinta o importanta deosebita in tehnica, datorita multiplelor avantaje legate de producerea, transportul, distributia si utilizarea energiei electrice.
O marime variabila este orice marime fizica a carei valoare este o functie de timp:
![]() (5.1)
(5.1)
 Valoarea instantanee este valoarea pe care o
marime variabila o are la un moment oarecare t. Aceasta se noteaza cu
litera mica a simbolului stabilit prin conventie pentru marimea respectiva (de
exemplu e - tensiunea electromotoare, u - tensiunea la borne, i
- intensitatea curentului, etc.).
Valoarea instantanee este valoarea pe care o
marime variabila o are la un moment oarecare t. Aceasta se noteaza cu
litera mica a simbolului stabilit prin conventie pentru marimea respectiva (de
exemplu e - tensiunea electromotoare, u - tensiunea la borne, i
- intensitatea curentului, etc.).
Marimea periodica este o marime variabila, ale carei valori instantanee se repeta la intervale egale de timp T (figura 5.1):
![]() (5.2)
(5.2)
unde k este un numar intreg si
T
este o
Perioada este cel mai mic interval de timp, dupa care valorile instantanee ale marimii respective se repeta in aceeasi ordine.
Frecventa unei marimi periodice reprezinta numarul de perioade in unitatea de timp:
![]() (5.3)
(5.3)
In SI, unitatea de masura frecventei, egala cu o perioada pe secunda, se nume hertz (Hz).
Pulsatia, sau frecventa unghiulara a marimii periodice este produsul:
![]() (5.4)
(5.4)
si se masoara in radiani pe secunda (rad/s).
Valoarea de varf a unei marimi periodice, este cea mai mare valoare instantanee atinsa in decursul unei perioade si se noteaza cu a.
Valoarea medie a unei marimi periodice este media aritmetica intr-un anumit interval de timp a valorilor instantanee ale marimii respective:
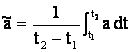 (5.5)
(5.5)
In cazul marimilor periodice, cand nu se mentioneaza explicit altfel, intervalul de timp se consider egal cu o perioada T
Valoarea medie a unei marimi periodice reprezinta inaltimea unui dreptunghi avand baza egala cu (t2 - t1) si care are aceeasi suprafata cu cea cuprinsa intre curba care reprezinta marimea periodica si axa absciselor (figura 5.1):
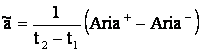 (5.6)
(5.6)
In relatia (5.6) ariile A+ si, respectiv, A- sunt modulele integralelor functiei i pe intervalele in care i > 0, si, respectiv i < 0.
Valoarea efectiva (eficace) a unei marimi periodice este radacina patrata a mediei patratelor valorilor instantanee in timp de o perioada:
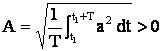 (5.7)
(5.7)
Valoarea efectiva se noteaza cu litera mare a simbolului marimii respective: E, U, I, etc.
Marimile periodice pot fi marimi periodice oarecare, marimi periodice alternative si marimi periodice pulsatorii.
Din cauza inertiei echipajului mobil, instrumentele electrice de masura indicatoare nu pot urmari variatiile instantanee ale marimilor periodice masurate. De aceea, ele sunt construite sa indice, de obicei, fie valori elective (cand au cuplul instantaneu proportional cu patratul marimii) fie valori medii (cand au cuplul instantaneu proportional cu marimea).
Marimea alternativa este acea marime periodica, a carei valoarea medie in decursul unei perioade este nula (figura 5.1):
![]() (5.8)
(5.8)
Marimea pulsatorie este marimea periodica a carei valoare instantanee nu isi schimba semnul, adica a > 0 sau a < 0.
Marimea sinusoidala (armonica) este o marime alternativa (figura 5.2) a carei expresie in functie de timp este:
![]() (5.9)
(5.9)
in care Amax > 0 se numeste amplitudine, si este modulul valorii maxime a marimii sinusoidale;
ω >0 este pulsatia, sau frecventa unghiulara;
(ωt+ φ) se numeste faza marimii sinusoidale si este argumentul dependent de timp (ωt+ φ)
al sinusului din relatia (5.9). Faza se exprima in radiani.
φ se numeste faza initiala a marimii sinusoidale este valoarea fazei in momentul initial
(t=0). Ea poate fi nula, negativa sau pozitiva (figura 5.3 a, b, c).
Daca se tine seama de relatia (5.2), rezulta egalitatea:
![]() (5.10)
(5.10)
care este satisfacuta pentru T = 2π.
Valoarea medie pe o perioada a unei marimi sinusoidale este, intotdeauna, nula:
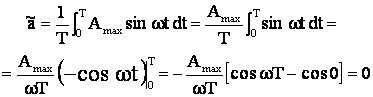 (5.11)
(5.11)
Din aceasta cauza, valoarea medie a unei marimi sinusoidale se calculeaza pe o jumatate de perioada:
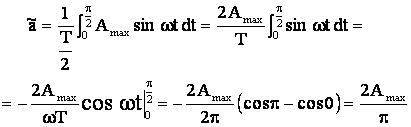 (5.12)
(5.12)
In calcule, s-a facut inlocuirea ![]()
Valoarea efectiva pentru o perioada a unei marimi sinusoidale se calculeaza cu relatia (5.7):

Cea de-a doua integrala de sub radical este nula:
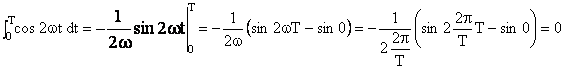
Astfel, valoarea efectiva pentru o perioada a unei marimi sinusoidale devine:
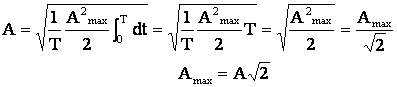 (5.13)
(5.13)
Valoarea efectiva a unui curent sinusoidal este numeric egala cu intensitatea unui curent continuu, care, strabatand aceeasi rezistenta ca si curentul periodic, dezvolta, in timp de o perioada, aceeasi cantitate de caldura:
 (5.14)
(5.14)
In consecinta, o marime sinusoidala poate fi scrisa sub forma:
![]() (5.15)
(5.15)
Sau, daca se face schimbarea de variabila ![]() , relatia (5.15) se poate scrie sub forma simplificata:
, relatia (5.15) se poate scrie sub forma simplificata:
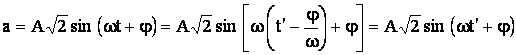 (5.16)
(5.16)
Aceasta expresie nu contine faza initiala si, cum alegerea originii timpului este arbitrara, rezulta ca faza initiala nu caracterizeaza proprietatile marimii a.
Prin urmare, numai diferentele relative ale fazelor initiale ale marimilor sinusoidale au o semnificatie fizica. De aceea, pentru una dintre marimile sinusoidale care intervin intr-o problema, faza initiala poate fi aleasa arbitrar (de obicei egala cu zero), astfel incat fazele initiale ale tuturor celorlaltor marimi vor fi univoc determinate. Marimea pentru care se alege faza initiala nula se numeste origine de faza.
Se considera doua marimi sinusoidale de aceea frecventa, dar cu faze initiale diferite. Cele doua marimi nu se anuleaza simultan si nu isi ating punctele de maxim si de minim simultan Se spune ca marimile sunt defazate intre ele.
![]()
![]()
Se numeste defazaj intre doua marimi sinusoidale diferenta fazelor acestora. Daca marimile au aceeasi frecventa, defazajul este egal cu diferenta fazelor lor initiale:
![]() (5.17)
(5.17)
Daca defazajul este pozitiv (![]() ), se spune ca marimea a1 este defazata inainte
fata de marimea a2 (figura 5.4). Daca defazajul este negativ (
), se spune ca marimea a1 este defazata inainte
fata de marimea a2 (figura 5.4). Daca defazajul este negativ (![]() ), marimea a1 este defazata in urma
marimii a2 sau marimea a2 este defazata inaintea
marimii a1. In cazul cand
), marimea a1 este defazata in urma
marimii a2 sau marimea a2 este defazata inaintea
marimii a1. In cazul cand ![]() marimile a1
si a2
sunt in faza. Daca defazajul
marimile a1
si a2
sunt in faza. Daca defazajul ![]() , se spune ca marimile a1 si a2
sunt in cuadratura, iar daca defazajul
, se spune ca marimile a1 si a2
sunt in cuadratura, iar daca defazajul ![]() , se spune ca marimile a1 si a2
sunt in opozitie de faza.
, se spune ca marimile a1 si a2
sunt in opozitie de faza.
In ecuatiile circuitelor electrice liniare de curent alternativ intervin operatiile elementare de adunare, scadere, inmultire cu un scalar, derivarea si integrarea. Prin aceste operatii liniare, efectuate cu marimi sinusoidale, se obtin tot marimi sinusoidale de aceea frecventa.
Adunarea a doua marimi sinusoidale de aceea frecventa:
![]()
![]()
conduce la marimea sinusoidala:
![]() (5.18)
(5.18)
in care A si tg φ se obtin prin identificare, dupa inlocuirea marimilor a1 si a2:
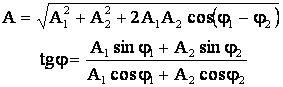 (5.19)
(5.19)
Amplificarea unei
marimi sinusoidale ![]() cu un scalar λ 0 conduce la o marime
sinusoidala de aceea frecventa si de aceeasi faza initiala:
cu un scalar λ 0 conduce la o marime
sinusoidala de aceea frecventa si de aceeasi faza initiala:
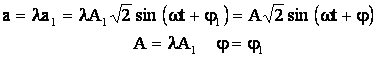 (5.20)
(5.20)
Derivarea unei
marimi sinusoidale ![]() conduce tot la o
marime sinusoidala de aceea frecventa, care are, insa, valoarea efectiva de
ω ori mai mare si care este defazata inainte cu
conduce tot la o
marime sinusoidala de aceea frecventa, care are, insa, valoarea efectiva de
ω ori mai mare si care este defazata inainte cu ![]() :
:
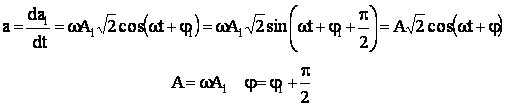 (5.20)
(5.20)
Integrarea unei marimi sinusoidale
unei ![]() conduce tot la o
marime sinusoidala de aceea frecventa, care are, insa, valoarea efectiva de
ω ori mai mica si care este defazata in urma cu
conduce tot la o
marime sinusoidala de aceea frecventa, care are, insa, valoarea efectiva de
ω ori mai mica si care este defazata in urma cu ![]() :
:
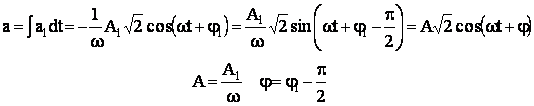 (5.21)
(5.21)
Fie un circuit simplu, liniar si pasiv, alimentat la borne
cu o tensiune sinusoidala de frecventa ![]() data:
data:
![]() (5.22)
(5.22)
Se pune problema de a determina expresia curentului de regim permanent din circuitul respectiv, care va avea aceeasi forma sinusoidala cu cea a tensiunii aplicate si aceeasi frecventa:
![]() (5.23)
(5.23)
Raportul pozitiv dintre valoarea efectiva a tensiunii si valoarea efectiva a curentului defineste impedanta circuitului si se noteaza cu Z:
![]() (5.23) Defazajul
φ
dintre tensiune si curent va fi:
(5.23) Defazajul
φ
dintre tensiune si curent va fi:
![]() 0 sau
0 sau ![]() (5.24) In
cadrul calculului acestor circuite se admit urmatoarele ipoteze
simplificatoare:
(5.24) In
cadrul calculului acestor circuite se admit urmatoarele ipoteze
simplificatoare:
circuitele sunt filiforme;
elementele de circuit sunt elemente ideale, adica rezistoarele au numai rezistenta, bobinele au numai inductivitate si condensatoarele au numai capacitate;
circuitul are parametri concentrati, adica in rezistorul R este concentrata intreaga rezistenta, in condensatorul C intreaga capacitate si in bobina L intreaga inductivitate a circuitului;
circuitul se considera izolat, adica asupra lui nu se exercita nici o actiune electromagnetica din partea altor circuite;
parametrii circuitului (R, L, C) sunt liniari, adica nu depind de intensitatea curentului sau de tensiune.
Aceste ipoteze vor fi luate in considerare la toate metodele de rezolvare a circuitelor, ele simplificand calculele, fara sa conduca la erori semnificative.
Se considera cunoscuta (a se consulta si capitolul 4) relatia tensiunilor, scrisa cu ajutorul teoremei II Kirchhoff, pentru un circuit alcatuit dintr-un rezistor ideal de rezistenta R, o bobina ideala de inductivitate L si un condensator ideal de capacitate C, conectate in serie:
![]()
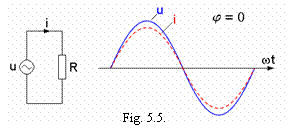 Circuitul cu rezistor ideal
Circuitul cu rezistor ideal Se considera un rezistor ideal de rezistenta R (figura 5.5), alimentat
cu tensiunea sinusoidala ![]() .
.
Ecuatia circuitului este
![]() (5.25)
(5.25)
Expresia curentului i din circuit va fi: de modificat desenele cu surse! ! !
![]() (5.26)
(5.26)
de unde se deduce ca:
![]() (5.27)
(5.27)
Rezulta ca, intr-un circuit cu rezistor ideal:
curentul i este in faza cu tensiunea u aplicata la borne (figura 5.5);
valoarea efectiva a curentului din circuit data de relatia 5.27 este independenta de frecventa tensiunii aplicate si are o expresie analoaga celei din curent continuu.
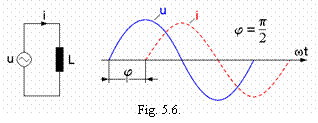
Se considera o bobina ideala de inductivitate L
(figura 5.6), alimentata cu tensiunea sinusoidala ![]() .
.
Ecuatia circuitului este:
![]() (5.28)
(5.28)
Expresia curentului i din circuit va fi:
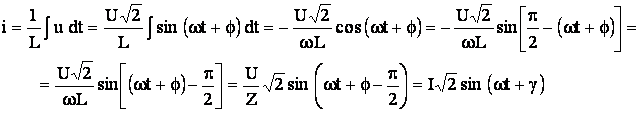 (5.29)
(5.29)
de unde se deduce ca:
![]() (5.30)
(5.30)
Marimea XL se numeste reactanta inductiva.
Rezulta ca, intr-un circuit cu bobina ideala:
curentul i este defazat cu ![]() in urma tensiunii u aplicate la borne (figura 5.6);
in urma tensiunii u aplicate la borne (figura 5.6);
valoarea efectiva a curentului din circuit este ![]() , adica este proportionala cu valoarea efectiva a tensiunii
aplicate si invers proportionala cu frecventa acesteia.
, adica este proportionala cu valoarea efectiva a tensiunii
aplicate si invers proportionala cu frecventa acesteia.
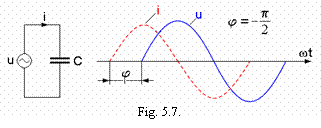 Circuitul cu condensator ideal
Circuitul cu condensator ideal Se considera un condensator ideal de capacitate C (figura 5.7), alimentat
cu tensiunea sinusoidala ![]() .
.
Ecuatia circuitului este:
![]()
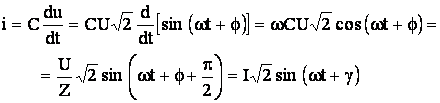 (5.31)
(5.31)
s![]() (5.32)
(5.32)
Marimea XC se numeste reactanta capacitiva.
Rezulta ca, intr-un circuit cu condensator ideal:
curentul i este defazat cu ![]() inaintea tensiunii u aplicate la borne (figura 5.6);
inaintea tensiunii u aplicate la borne (figura 5.6);
valoarea efectiva a curentului din circuit este ![]() , adica este proportionala cu valoarea efectiva a tensiunii
aplicate si cu frecventa acesteia.
, adica este proportionala cu valoarea efectiva a tensiunii
aplicate si cu frecventa acesteia.
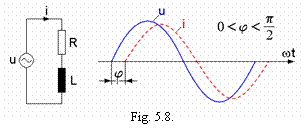 Se considera un circuit
alcatuit dintr-un rezistor ideal de
rezistenta R si o bobina ideala
de inductivitate L conectate in serie (sau doar dintr-o bobina reala de rezistenta R si de inductivitate L)
(figura 5.8), alimentat cu tensiunea sinusoidala
Se considera un circuit
alcatuit dintr-un rezistor ideal de
rezistenta R si o bobina ideala
de inductivitate L conectate in serie (sau doar dintr-o bobina reala de rezistenta R si de inductivitate L)
(figura 5.8), alimentat cu tensiunea sinusoidala ![]() .
.
Ecuatia circuitului este:
![]()
![]() (5.33)
(5.33)
Curentul de regim permanent va fi dat de o solutie
particulara a ecuatie integro-diferentiale (5.33), care trebuie sa fie de forma
![]() , pe care, substituind-o in ecuatia (5.33) se obtine
identitatea:
, pe care, substituind-o in ecuatia (5.33) se obtine
identitatea:
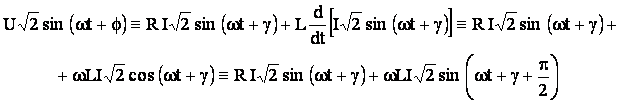
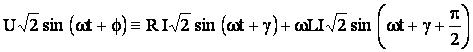 (5.34)
(5.34)
Identitatea (5.34) trebuie sa fie satisfacuta pentru orice
valori ale variabilei t, inclusiv pentru momentele
particulare in care ![]() si
si ![]() . Prin inlocuirea acestor valori particulare in relatia
(5.34), si, facandu-se notatia
. Prin inlocuirea acestor valori particulare in relatia
(5.34), si, facandu-se notatia ![]() , rezulta egalitatile:
, rezulta egalitatile:
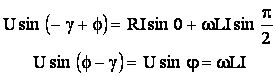 (5.35)
(5.35)
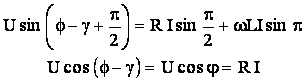 (5.36)
(5.36)
Prin ridicarea la patrat a relatiilor (5.35) si (5.36) si prin adunarea lor se obtine:
![]()
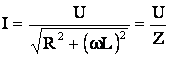 (5.37)
(5.37)
unde Z este impedanta circuitului, care este data de relatia:
![]() (5.38)
(5.38)
Rezulta, de asemenea, ca:
![]() cu
cu 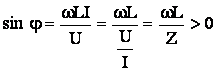 si
si 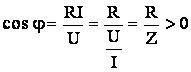 (5.39)
(5.39)
|
Tabelul 5.1. | |||||||||
|
- 0 |
- π/2 |
- π |
- 3π/2 |
- 2π | |||||
|
sin | |||||||||
|
cos | |||||||||
|
tg | |||||||||
|
ctg | |||||||||
Conform tabelului 5.1., aceste conditii sunt indeplinite simultan doar daca:
![]() (5.40)
(5.40)
Tinandu-se seama de relatiile (5.37), (5.39) si de notatia ![]() , de unde rezulta ca
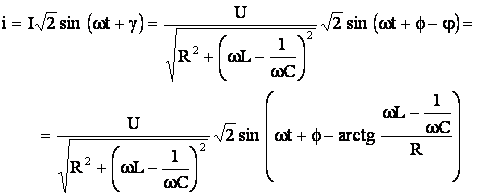
, de unde rezulta ca ![]() , expresia valorii instantanee a curentului este:
, expresia valorii instantanee a curentului este:
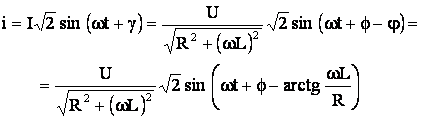 (5.41)
(5.41)
Rezulta ca, intr-un circuit serie cu rezistor si bobina ideale (sau intr-un circuit cu bobina reala):
 curentul i
este defazat cu un unghi
curentul i
este defazat cu un unghi ![]() in urma tensiunii u
aplicate la borne (figura 5.8), unghi a carui valoare creste cu frecventa,
tinzand catre
in urma tensiunii u
aplicate la borne (figura 5.8), unghi a carui valoare creste cu frecventa,
tinzand catre![]() atunci cand
atunci cand ![]() ; atunci cand
; atunci cand ![]() unghiul
unghiul ![]() ;
;
valoarea efectiva a curentului din circuit scade cu cresterea
frecventei, tinzand asimptotic catre 0 atunci cand ![]() .
.
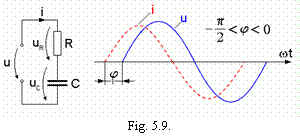
Se considera un circuit alcatuit
dintr-un rezistor ideal de rezistenta
R
si un condensator ideal de capacitate
C
conectate in serie (figura 5.9), alimentat cu tensiunea sinusoidala ![]() .
.
Ecuatia circuitului este:
![]()
![]() (5.42)
(5.42)
Curentul de regim permanent va fi dat de o solutie
particulara a ecuatie integro-diferentiale (5.33), care trebuie sa fie de forma
![]() , pe care, substituind-o in ecuatia (5.33) se obtine identitatea:
, pe care, substituind-o in ecuatia (5.33) se obtine identitatea:

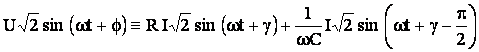 (5.43)
(5.43)
Se pun conditiile ca identitatea (5.43) sa fie satisfacuta
pentru momentele particulare in care ![]() si
si ![]() si se tine seama de
notatia
si se tine seama de
notatia ![]() . Astfel, rezulta:
. Astfel, rezulta:
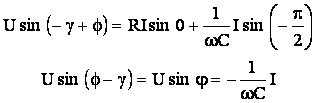 (5.44)
(5.44)
![]() (5.45)
(5.45)
Prin ridicarea la patrat a relatiilor (5.44) si (5.45) si prin adunarea lor se obtine:
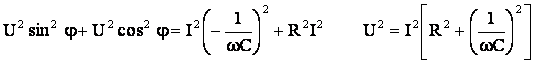
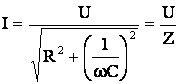 (5.46)
(5.46)
unde Z este impedanta circuitului, care este data de relatia:
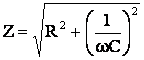 (5.47)
(5.47)
De asemenea, rezulta ca:
![]()
cu 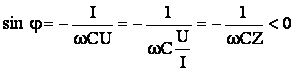 si
si 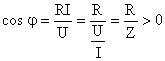 (5.48)
(5.48)
Conform tabelului 5.1., aceste conditii sunt indeplinite simultan doar daca:
![]() (5.49)
(5.49)
Tinandu-se seama de relatiile (5.44), (5.45) si de notatia ![]() , de unde rezulta ca
, de unde rezulta ca ![]() , expresia valorii instantanee a curentului este:
, expresia valorii instantanee a curentului este:
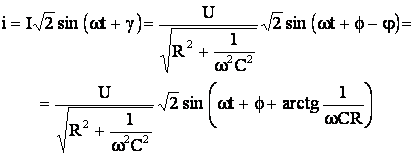 (5.50)
(5.50)
Rezulta ca, intr-un circuit serie cu rezistor si condensator ideale:
curentul i este defazat cu un unghi ![]() inaintea tensiunii u
aplicate la borne (figura 5.8), unghi a carui valoare scade cu frecventa,
tinzand catre
inaintea tensiunii u
aplicate la borne (figura 5.8), unghi a carui valoare scade cu frecventa,
tinzand catre ![]() atunci cand
atunci cand ![]() ; iar atunci cand
; iar atunci cand ![]() unghiul
unghiul ![]() ;
;
valoarea efectiva a curentului din circuit creste cu cresterea
frecventei, tinzand asimptotic catre ![]() atunci cand
atunci cand ![]() .
.
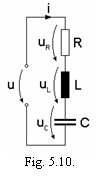 Circuitul serie cu rezistor ideal, bobina ideala si condensator ideal
Circuitul serie cu rezistor ideal, bobina ideala si condensator ideal Se considera un circuit alcatuit
dintr-un rezistor ideal de rezistenta
R,
o bobina ideala de inductivitate L
si un condensator ideal de capacitate
C
conectate in serie (figura 5.10), alimentat cu tensiunea sinusoidala ![]() .
.
Ecuatia circuitului este:
![]()
![]() (5.51)
(5.51)
Curentul de regim permanent va fi dat de o solutie
particulara a ecuatie integro-diferentiale (5.51), care trebuie sa fie de forma
![]() , pe care, substituind-o in ecuatia (5.51) se obtine
identitatea:
, pe care, substituind-o in ecuatia (5.51) se obtine
identitatea:
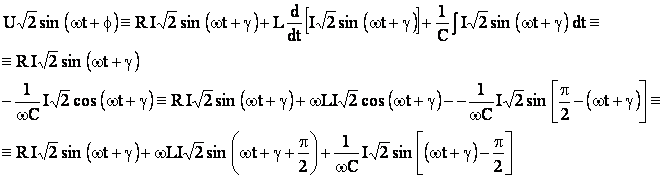
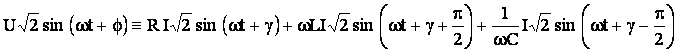 (5.52)
(5.52)
Se pun conditiile ca identitatea (5.52) sa fie satisfacuta
pentru momentele particulare in care ![]() si
si ![]() si se tine seama de
notatia
si se tine seama de
notatia ![]() . Astfel, rezulta:
. Astfel, rezulta:
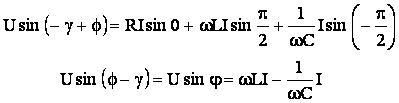 (5.53)
(5.53)
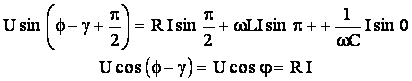 (5.54)
(5.54)
Prin ridicarea la patrat a relatiilor (5.35) si (5.36) si prin adunarea lor se obtine:
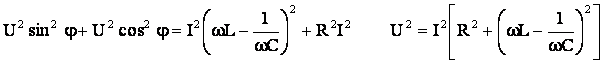
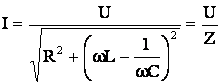 (5.55)
(5.55)
unde Z este impedanta circuitului, care este data de relatia:
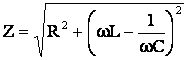 (5.56)
(5.56)
Rezulta, de asemenea, ca:
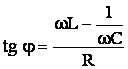
cu 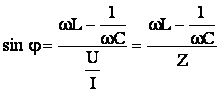 0 si
0 si (5.57)
(5.57)
Conform tabelului 5.1., aceste conditii sunt indeplinite simultan doar daca:
![]() (5.58)
(5.58)
Tinandu-se seama de relatiile (5.53), (5.54) si de notatia ![]() , de unde rezulta ca
, de unde rezulta ca ![]() , expresia valorii instantanee a curentului este:
, expresia valorii instantanee a curentului este:
 (5.59)
(5.59)
Se observa faptul ca acest circuit reprezinta cazul general al unei laturi de circuit de curent alternativ, deoarece nu exista vreun circuit cu o structura mai complexa decat a acestuia. De aici rezulta ca toate celelalte circuite prezentate reprezinta cazuri particulare ale acestui circuit serie alcatuit dintr-un rezistor ideal, o bobina ideala si un condensator ideal.
Pentru circuite simple, metoda substitutiei solutiilor sinusoidale permite, cu destula usurinta, determinarea curentului de regim permanent. Pentru circuite complexe, insa, calculele devin mai complicate, nepermitand o vedere de ansamblu asupra proprietatilor calitative ale circuitului, motiv pentru care, in aceste cazuri se utilizeaza alte metode, care vor fi prezentate in cele ce urmeaza.
Pentru o frecventa data, caracterizarea unui circuit liniar de curent alternativ sinusoidal, care nu are cuplaje magnetice cu exteriorul, se poate face cu ajutorul a numai doi parametri. Exista mai moduri de alegere a acestei perechi de parametri.
Impedanta circuitului, notata cu Z, a fost definita anterior, cu ajutorul relatiei (5.23), ca raportul pozitiv dintre valoarea efectiva a tensiunii si valoarea efectiva a curentului:
![]()
Impedanta depinde, in general, de parametrii circuitului (R, L, C) si de frecventa. In SI, impedanta se masoara, ca si rezistenta, in ohmi (Ω).
De asemenea, defazajul φ dintre tensiune si curent a fost definit anterior cu ajutorul relatiei (5.24):
![]() 0 sau
0 sau ![]()
Defazajul circuitului depinde, de asemenea, de parametrii circuitului (R, L, C) si de frecventa. In SI, defazajul se masoara in radiani.
Pentru caracterizarea unui circuit liniar de curent alternativ sinusoidal, in locul parametrilor Z si φ, se mai pot folosi parametrii rezistenta si reactanta.
Rezistenta R a unui circuit liniar de curent alternativ sinusoidal este data de relatia:
![]() (5.60)
(5.60)
in care ![]() se mai numeste si componenta activa a tensiunii aplicate
(care este in faza cu curentul din circuit). Aceasta marime nu trebuie
confundata cu rezistenta definit prin legea conductiei electrice (definita in
cazul curentului continuu). Ele coincid numai in anumite cazuri particulare.
se mai numeste si componenta activa a tensiunii aplicate
(care este in faza cu curentul din circuit). Aceasta marime nu trebuie
confundata cu rezistenta definit prin legea conductiei electrice (definita in
cazul curentului continuu). Ele coincid numai in anumite cazuri particulare.
Reactanta X a unui circuit liniar de curent alternativ sinusoidal este data de relatia:
![]()
in care ![]() se mai numeste si componenta reactiva a tensiunii aplicate
(care este in cuadratura cu curentul din circuit, adica defazata cu
se mai numeste si componenta reactiva a tensiunii aplicate
(care este in cuadratura cu curentul din circuit, adica defazata cu ![]() fata de curentul din circuit).
fata de curentul din circuit).
In SI, rezistenta si reactanta se masoara in ohmi (Ω).
Intre impedanta si defazaj, pe de-o parte, si rezistenta si
reactanta, pe de alta parte, exista urmatoarele relatii de calcul: ![]() (5.60)
(5.60)
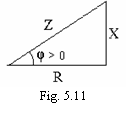 Aceste relatii se retin comod cu ajutorul asa-numitului triunghi al impedantelor (figura 5.11).
Aceste relatii se retin comod cu ajutorul asa-numitului triunghi al impedantelor (figura 5.11).
Valoarea instantanee a curentului din circuit, exprimata in functie de rezistenta si reactanta, este:
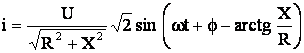 (5.61)
(5.61)
Admitanta circuitului este marimea inversa (reciproca) impedantei:
![]() (5.62)
(5.62)
Impreuna cu defazajul, admitanta poate caracteriza complet circuitul respectiv.
Conductanta circuitului este marimea definita prin relatia:
![]() (5.63)
(5.63)
unde ![]() se numeste componenta activa a curentului.
se numeste componenta activa a curentului.
In general, conductanta nu este egala cu valoarea inversa (reciproca) a rezistentei definite prin relatia (5.60) si nu trebuie confundata nici cu conductanta definita in curent continuu, cu care coincide numai in anumite cazuri particulare.
Susceptanta circuitului este marimea definita prin relatia:
![]()
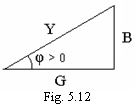 unde
unde ![]() se numeste componenta reactiva a curentului.
se numeste componenta reactiva a curentului.
![]() In SI, admitanta, conductanta si susceptanta se masoara in siemens (S).
In SI, admitanta, conductanta si susceptanta se masoara in siemens (S).
Intre admitanta si defazaj, pe de-o parte, si conductanta si susceptanta, pe de alta parte, exista urmatoarele relatii de calcul:
![]() (5.64)
(5.64)
De asemenea, intre impedanta, , rezistenta, reactanta, admitanta conductanta si susceptanta, exista urmatoarele relatii de calcul:
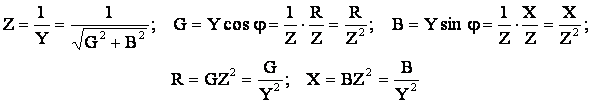 (5.65)
(5.65)
Aceste relatii se retin comod cu ajutorul asa-numitului triunghi al admitantelor (figura 5.12).
Valoarea instantanee a curentului din circuit, exprimata in functie de conductanta si susceptanta, este:
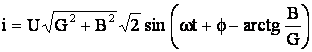 (5.66)
(5.66)
Pentru o frecventa (pulsatie) data, circuitele de curent alternativ sinusoidal pot fi:
circuite rezistive (sau aflate la rezonanta), pentru care φ = 0; Z = R; X = B = 0. Curentul din circuit si tensiunea aplicata sunt in faza.
circuite inductive, pentru care φ > 0; X > 0; B > 0.
Defazajul pozitiv se mai numeste defazaj inductiv, iar curentul este defazat in
urma tensiunii (cazul circuitului cu bobina reala). Daca ![]() , circuitul se numeste pur inductiv (cazul circuitului cu
bobina ideala)
, circuitul se numeste pur inductiv (cazul circuitului cu
bobina ideala)
circuite capacitive, pentru care φ < 0; X < 0; B < 0.
Defazajul negativ se mai numeste defazaj capacitiv, iar curentul este inaintea
tensiunii. Daca ![]() , circuitul se numeste pur capacitiv (cazul circuitului cu
condensator ideal)
, circuitul se numeste pur capacitiv (cazul circuitului cu
condensator ideal)
Se considera un circuit oarecare
(figura 5.13.a), alimentat cu tensiunea sinusoidala ![]() . Curentul de regim permanent va fi de forma
. Curentul de regim permanent va fi de forma ![]() .
.
Puterea instantanee primita de circuit de la sursa pe la borne este egala, conform teoremei transferului de putere, cu produsul dintre valorile instantanee ale tensiunii si curentului:
![]() (5.67)
(5.67)
si este (algebric) putere primita, respectiv cedata, dupa cum sensurile tensiunii si curentului se asociaza dupa regula de la receptoare (relatia 2.48) sau, respectiv, dupa regula de la generatoare (relatia 2.46). Prin inlocuirea expresiilor tensiunii si curentului in relatia se obtine:
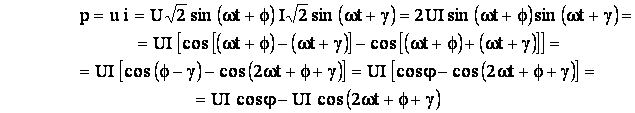 (5.68)
(5.68)
S-a tinut seama de notatia ![]() si s-a utilizat
relatia din trigonometrie, conform careia:
si s-a utilizat
relatia din trigonometrie, conform careia:
![]()
Puterea instantanee este, deci, o marime periodica, avand o componenta constanta si o componenta de frecventa dubla fata de cea a tensiunii de alimentare si a curentului din circuit.
Se numeste putere activa si se noteaza cu P valoarea medie a puterii instantanee p luata pentru un numar intreg de perioade:
![]() (5.69)
(5.69)
Prin integrare, rezulta expresia puterii active:
 (5.70)
(5.70)
In SI, puterea activa, ca si puterea instantanee se masoara in watt (W), care este o unitate de masura mica, mai ales in energetica, unde se utilizeaza multiplii acesteia: kilowatt-ul (1 kW=103 W, megawatt-ul (1MW = 106 W), gigawatt-ul (1 GW =109 W).
Relatia (5.69) este relatia generala de definitie a puterii active, valabila pentru o retea oarecare si in regim periodic nesinusoidal, in timp ce relatia (5.70) este relatia de calcul a puterii active in regim sinusoidal pentru un dipol, adica pentru o retea cu doua borne (in curent alternativ monofazat, de exemplu).
Puterea activa primita de un dipol pasiv este intotdeauna pozitiva, cel mult nula, daca circuitul nu contine rezistoare. Puterea activa se mai poate exprima si cu ajutorul rezistentei sau conductantei:
![]() (5.71)
(5.71)
Aceasta expresie e nula pentru circuitele nedisipative sau pur reactive (adica pentru circuitele care, in medie, nu absorb putere activa din exterior) si este pozitiva pentru circuitele disipative.
Expresia (5.68) a puterii instantanee arata ca aceasta oscileaza cu frecventa unghiulara 2ω in jurul valorii ei medii, care este puterea activa (figura 5.13.b). Chiar daca circuitul este un receptor pasiv, pentru care puterea activa primita este intotdeauna pozitiva (P > 0), exista momente in decursul unei perioade, cand puterea instantanee primita este negativa, adica este, de fapt, cedata spre exterior. In acele momente, energia acumulata in campul magnetic al bobinelor sau in campul electric al condensatoarelor este restituita, partial, sursei de alimentare. In figura 5.13 c sunt indicate sensurile instantanee reale ale tensiunii, curentului si puterii in diferite momente ale unei perioade.
Se numeste putere aparenta a unui dipol electric marimea definita ca produsul valorilor efective ale tensiunii si curentului:
![]() (5.72)
(5.72)
In SI, puterea aparenta se masoara in volt-amper (VA), care este o unitate de masura mica, mai ales in energetica, unde se utilizeaza multiplii acesteia: kilovolt-amper-ul (kVA), (1 kVA=103 VA, megavolt-amper-ul (1MVA = 106 VA), gigavolt-amper-ul (1 GVA =109 VA).
Puterea aparenta se poate exprima si cu ajutorul marimilor impedanta si admitanta:
![]() (5.73)
(5.73)
Se numeste factor de putere raportul pozitiv si subunitar dintre puterea activa si puterea aparenta:
![]() (5.74)
(5.74)
Pentru un dipol electric, in regim sinusoidal, factorul de putere are expresia:
![]() (5.75)
(5.75)
Se numeste putere reactiva a unui dipol electric marimea definita de relatia:
![]()
In SI, puterea reactiva se masoara in voltamper reactiv (var), care este o unitate de masura mica, mai ales in energetica, unde se utilizeaza multiplii acesteia: kilovolt-amper-ul reactiv (1 kvar=103 var), megavolt-amper-ul reactiv (1Mvar = 106 var), gigavolt-amper-ul reactiv(1 Gvar =109 var).
Intre puterile activa, reactiva si aparenta exista relatiile:
![]()
![]() (5.76)
(5.76)
Aceste relatii se retin comod cu ajutorul asa-numitului triunghi al puterilor (figura 5.13).
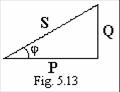 Puterea reactiva primita de
catre un dipol pasiv (pozitiva in cazul circuitelor inductive si negativa in
cazul circuitelor capacitive) se poate exprima cu ajutorul reactantei si
susceptantei, sub formele:
Puterea reactiva primita de
catre un dipol pasiv (pozitiva in cazul circuitelor inductive si negativa in
cazul circuitelor capacitive) se poate exprima cu ajutorul reactantei si
susceptantei, sub formele:
![]()
Puterea reactiva este nula pentru circuitele rezistive.
Referitor la sensul real de transmisie a puterii reactive se fac urmatoarele precizari.
La circuitele receptoare (la care sensurile de referinta ale tensiunii u si curentului i sunt asociate dupa regula de la receptoare):
daca Q = UI sin φ > 0, puterea reactiva este absorbita de la reteana exterioara;
daca Q = UI sin φ < 0, puterea activa este cedata retelei exterioare.
La circuitele generatoare (la care sensurile de referinta ale tensiunii u si curentului i sunt asociate dupa regula de la generatoare):
daca Q = UI sin φ > 0, puterea reactiva este cedata retelei exterioare;
daca Q = UI sin φ < 0, puterea reactiva este absorbita de la reteaua exterioara.
In cazul unor circuite capacitive (sau in cazul particular al unor condensatoare) (X < 0) si Q < 0 (cu regula de la receptoare), rezultand ca aceste circuite (in particular condensatoarele) sunt producatoare de putere reactiva.
Similar, circuitele inductive (in particular bobinele), pentru care (X > 0) si Q > 0, sunt consumatoare de putere reactiva.
Functiile sinusoidale, ca si vectorii liberi in plan, sunt complet caracterizate de doua valori scalare, si anume de un numar pozitiv si de valoarea unui unghi. Unei marimi electrice sinusoidale (curent sau tensiune) i se poate asocia, deci, fara restrictii, un vector liber in plan, si reciproc. Deci, functiile sinusoidale pot fi puse in corespondenta biunivoca cu vectori liberi in plan, fapt ce face ca relatiilor analitice dintre marimile sinusoidale sa le corespunda relatii geometrice mai simple si mai intuitive intre vectorii asociati. Acest gen de reprezentare simbolica este o re-prezentare geometrica.
Se mai cunoaste faptul ca fiecarui numar complex ii corespunde, biunivoc, un punct in plan, numitafixul acelui numar, deci, implicit si vectorul de pozitie al acelui punct.In acest mod functiile sinusoidale pot fi puse in corespondenta biunivoca si cu numere complexe, ceea ce face ca ecuatiile integro-diferentiale liniare, cu coeficienti constantiale circuitelor sa se reduca la ecuatii algebrice liniare de ordinul I. Acest gen de reprezentare simbolica este o reprezentare analitica. In continuare va fi prezentata metoda de reprezentare analiticacu ajutorul numerelor complexe si a vectorilor de pozitie atasati acestora.
O funtie sinusoidala de timp, de frecventa data este complet caracterizata prin doua valori scalare : modulul si argumentul sau. Se poate, deci, asocia fiecarei marimi sinusoidale un numar complex, aceasta asociere fiind biunivoca.
Fie o functie sinusoidala de timp a(t) :
![]()
Imaginea sa in complex, notata cu A, este un numar constant, avand modulul egal cu valoarea efectiva si argumentul egal cu faza initiala a marimii respective :
![]() (5.77)
(5.77)
In exprimarea curenta se utilizeaza formularea prescurtata curent complex (in loc de imaginea in complex a curentului), sau tensiune complexa (in loc de imaginea in complex a tensiunii).
Aplicand formula lui Euler relatiei (5.77), inmultite, in
prealabil, cu ![]() , se obtine :
, se obtine : ![]()
Se observa faptul ca partea imaginara a acestei expresii reprezinta tocmai functia sinusoidala de timp a(t). Deci regula trecerii inverse (de la imaginea complexa) la marimea sinusoidala este :
![]() (5.78)
(5.78)
In planul complex marimea sinusoidala a(t) va fi reprezentata printr-un vector fix (numit in acest cazfazor), avand modulul egal cu valoarea efectiva si argumentul egalcu faza initiala a marimii (figura 5.14).
Marimile sinusoidale origine de faza au imagini reale, adica fazorii lor asociati au aceeasi directie si acelasi sens cu axa reala.
Defazajul φ12 dintre marimile sinusoidale a1 si a2 :
![]()
![]()
este egal cu diferenta argumentelor imaginilor lor in complex, adica cu argumentul catului lor :
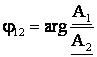
Corespondenta intre operatiile cu marimi sinusoidale si operatiile cu imaginile lor in complex este urmatoarea :
Adunarea a doua marimi sinusoidale a1 si a2 corespunde biunivoc cu adunarea imaginilor in complex ale acestora si cu adunarea vectoriala a fazorilor corespunzatori :
![]() (5.80)
(5.80)
Aceasta proprietate rezulta din faptul ca partea imaginara a unei sume este egala cu suma partilor imaginare ale termenilor sumei respective.
Amplificarea cu un scalar real λ a unei marimi sinusoidale a corespunde biunivoc cu inmultirea fazorului corespunzator marimii in complex a acesteia cu acel scalar :
![]() (5.81)
(5.81)
Aceasta proprietae este evidenta, daca se are in vedere regula de reprezentare in complex a marimilor sinusoidale.
Derivarea in raport cu timpul a unei marimi sinusoidale corespunde biunivoc cu rotirea in sens trigonometric (antiorar) a fazorului corespunzator marimii si inmultirea imaginii tn complex a acesteia cu numarul complex jω :
![]()
Intr-adevar, daca ![]() , prin derivare, se obtine :
, prin derivare, se obtine :
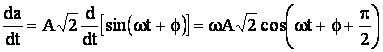
Imaginea in complex a ultimei expresii a derivatei este urmatoarea :
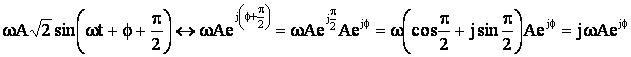
Integrarea in raport cu timoul a unei marimi sinusoidale corespunde biunivoc cu rotirea in sens invers trigonometric(orar) a fazorului corespunzator marimii si cu impartirea imaginii in complex a acesteia cu numarul comlaplex jω :
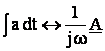 (5.83)
(5.83)
Prin integrarea marimii
sinusoidale ![]() , se obtine :
, se obtine :
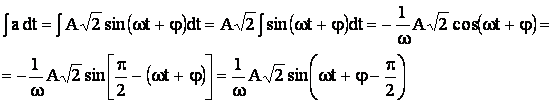
Imaginea in complex a ultimei expresii a integralei este urmatoarea :
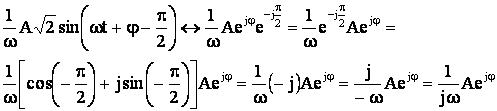
Se observa, deci, ca operatiilor elementare efectuate cu marimi sinusoidale le corespund, fara exceptie, operatii algebrice efectuate cu imaginile in complex ale acestor marimi.
Metoda reprezentarii in complex prezinta avantajul principal de a transforma ecuatiile integro-diferentiale ale circuitelor in ecuatii algebriceale imaginilor in complex ale marimilor sinusoidale(curenti si tensiuni).
Repreyentarea in complex preyentata se numeste repreyentare in complex simplificat si poate fi utilizata numai in problemele in care diferitele marimi sinusoidale au aceea frecventa f (respectiv aceeasi pulsatie ω). In caz contrar se utilizeaza o alta varianta a reprezentarii in complex, denumita repreyentare in complex generalizata sau (nesimplificata), in care imaginea in complex a unei marimi sinusoidale a este o functie complexa de timp, avand modulul egal cu amplitudinea marimii sinusoidale si argumentul egal cu faza acesteia :
![]() (5.84)
(5.84)
In cazul reprezentarii in complex generalizat (sau nesimplificat),corespondenta operatiilor este identica cu cea intalnita la reprezentarea in complex simplificat.
Metodologia de rezolvare a circuitelor de curent alternativ folosind reprezentarea in complex este urmatoarea :
Se scriu ecuatiile integro-diferentiale ale circuitelor in valori instantanee ;
Se determina imaginile in complex ale marimilor sinusoidale date si ale ecuatiilor integro-diferentiale, termen cu termen, inlocuind derivarile prin inmultiri cu jω si integrarile prin imartiri cu jω.
Se rezolva ecuatiile algebrice obtinute, in raport cu imaginile functiilor necunoscute ;
Se determina marimile sinusoidale necunoscute cu regula trecerii inverse data de relatia (5.78)
De obicei, in paralelcu acest calcul, se efectueaza si reprezentarea fazoriala a marimilor sinusoidale, obtinandu-se, in planul complex, asa numitele diagrame de fazori", care ilustreaza sugestivrelatiile de faza dintre diferitele marimi reprezentate.
Se considera un dipol electric receptor, liniar si pasiv, la bornele caruia se aplica tensiunea sinusoidala :
![]() (5.85)
(5.85)
Circuitul absoarbe curentul d regim permanent :
![]()
Se numeste independenta complexa raportul dintre tensiunea complexa aplicata la bornele circuitului si curentul complex corespunzator :
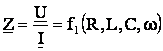
Independenta complexa este o marime caracteristica circuitului, depinzand numai de parametrii elementelor de circuit si de frecventa. Inlocuind (5.87) expresiile imaginilor complese(simplificate sau nesimplificate) ale tensiunii u si curentuli i se obtine :
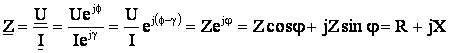 (5.88)
(5.88)
In relatia (5.88) s-a tinut seama ca defazajul φ dintre tensiune si curent a fost definit anterior cu ajutorul relatiei (5.24) Φ - γ = φ, iar prin prelucrarea grupului de relatii (5.60) rezulta expresiile rezistentei si reactantei in functie de impedanta si de unghiul de defayaj dintre curent si tensiune R = Zcosφ si X = Zsinφ.
Impedanta complexa are modului egal cu impedanta circuitului, argumentul egal cu defazajul circuitului, partea reala egala cu rezistenta si coeficientul partii imaginare ehal cu reactanta circuitului. In consecinta, impedanta complexa permite o caracterizare completa a circuitului considerat, la o frecventa data deoarece permite deducerea tuturor parametrilor reali ai circuitului :
![]() (5.89)
(5.89)
Trebuie men'ionat faptul ca impedanta complexa nu este o repreyentare in complex a raportului valorilor instantanee ale tensiunii si curentului (raport care nu este o marime sinusoidalaz) sau a vreunei alte marimi sinusoidale. Impedanta complexa este un parametru complex, utilizat in ecuatii ca un operator de calcul.
Se numeste admitanta complexa raportul dintre curentul complex si tensiunea complexa aplicata la bornele circuitului, fiind egala cu valoarea inversa a impedantei complexe :
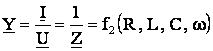 (5.90)
(5.90)
Ca si independenta complexa, admitanta complexa este o marime caracteristica circuitului, depinzand numai de parametrii elementelor de circuit si de fercventa. Inlocuind in relatia (5.89) expresiile imaginilor complexe (simplificate sau nesimplificate) ale tensiunii u si curentului I, se obtine :
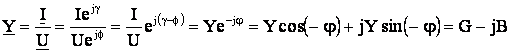 (5.91)
(5.91)
In relatia (5.91) s-a tinut seama de faptul ca defazajul φ dintre tensiune si curent a fost definit anterior cu ajutorul relatiei (5.24) Φ - γ φ , iar prin prelucrarea grupului de relatii (5.64), rezulta expresiile conductantei si susceptantei in functie de admitanta si de unghiul de defazaj dintre curent si tensiune G = Ycosφ si B = Y sinφ.
Admitanta complexa are modulul egal cu admitanta circuitului, argumentul egal cu defazajul cu semn schimbat, partea reala egala cu conductanta si partea imaginara egala cu susceptanta cu semn schimbat a circuitului :
![]() (5.92)
(5.92)
Atat impedanta complexa, cat si admitanta complexa pot fi reprezentate grafic intr-un plan complex al impedantelor, respectiv al admitantelor, in care afixele corspunzatoare se afla, intotdeauna, in semiplanul drept, inclusiv axa imaginara, deoarece R > 0 si G > 0.
Puterea complexa
Puterea instantanee p la bornele unui dipol generator sau receptor este, conform relatiei (5.68) :
![]()
Aceasta nu poate fi reprezentata in complex, dupa regulile stabilite, deoarece nu este o marime sinusoidala. Se poate defini, insa o putere complexa, din care se deduc comod puterea activa, puterea reactiva si puterea aparenta.
Se numeste putere complexa S produsul dintre tensiunea complexa si curentul complex conjugat :
![]() (5.93)
(5.93)
Inlocuind expresiile imaginilor in complex ale tensiunii si curentului, se obtine:
![]() (5.94)
(5.94)
Puterea complexa are modulul egal cu puterea aparenta, argumentul egal cu defazajul circuitului, partea reala egala cu puterea activa si coeficientul partii imaginare egal cu puterea reactiva :
![]() (5.95)
(5.95)
Puterea complexa mai poate fi exprimata astfel :
![]() (5.96)
(5.96)
Puterea complexa S poate fi reprezentata grafic in planul complex al puterilor. In cazul unui circuit pasiv afixul puterii complexe se gaseste in semiplanul drept (P 0 ; Q 0) iar in cazul unui circuit activ pozitia afixului puterii complexe poate fi oricare (P 0 ; Q
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 4474
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved