DISTRIBUTIA TRANZITORIE DE TEMPERATURA INTR-O PLACA METALICA SUBTIRE

DISTRIBUTIA TRANZITORIE DE TEMPERATURA INTR-O PLACA METALICA SUBTIRE

O placa metalica se gaseste initial la o temperatura uniforma de 200ºC. La momentul t=0 temperatura peretelui de est a placii este brusc redusa la 0C. Alte fete ale placii sunt izolate . Utilizand schema explicita a metodei volumelor finite, pentru un pas de timp adecvat, pentru calculul distributiei tranzitorii a temperaturii si comparati rezultatele cu solutia analitica la momentele t=40s , t=80s, t=120s.

Solutie:

Ecuatia diferentiala ce guverneaza transferul termic este:

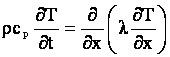
Conditia initiala : T = 200ºC la t=0

Conditiile la limita : = 0 pentru x = 0, t > 0

T = 0 pentru x = L, t > 0

Solutia analitica :

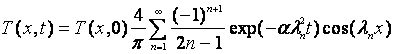
λ_n =    

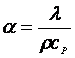
Se utilizeaza o retea de discretizare cu 6 noduri uniform distribuite ca in figura :

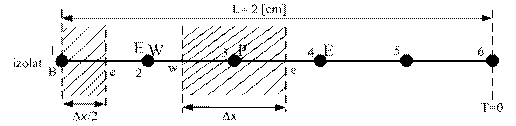
Pentru un nod interior ecuatia discretizata este :

Daca se considera _{e w} si A_e = A_w = A atunci se obtine :

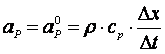
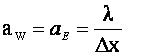
Ecuatia este valabila pentru nodurile 2,3,4,5.

Pentru nodul 1 (nodul situate pe frontiera) se integreaza ecuatia pe jumatate de volum de control.

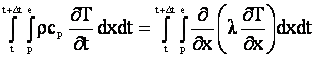
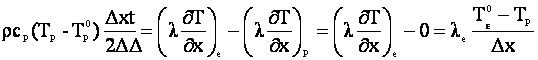
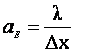
Pentru nodul 5 este valabila aceeasi ecuatie ca pentru un nod interior cu observatia ca termenul ce contine frontiera trece ca termen sursa suplimentar :

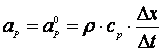
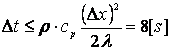
Se alege Δt = 2 [s] si se obtine :

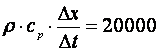
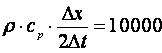
Dupa inlocurea valorilor numerice in ecuatii si simplificand vom obtine:

Nodul 1 :   

Nodul 2, 3, 4 :

Nodul 5 :

Comparatie : solutia numerica - solutia analitica:

Se reprezinta grafic si se compara solutia analitica cu cea numerica:

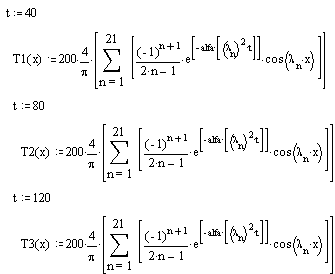
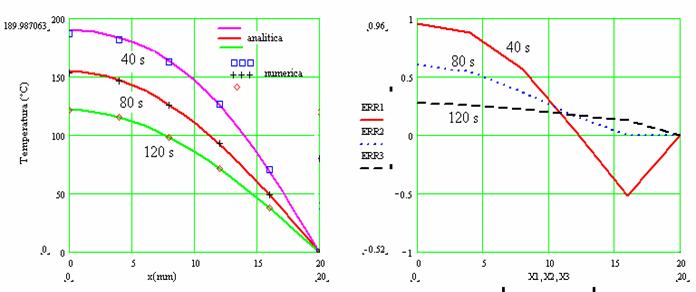
Programul in Fortran

PROGRAM PROBLEMA4

PARAMETER (nn = 21, npt =12000)

DOUBLE PRECISION TEMP(npt+1,nn), AX(nn)

DOUBLE PRECISION DX, ALFA, RCP, TC, TI, L, DT, CRS

DOUBLE PRECISION ap, ap0, aw, ae

c    DOUBLE PRECISION t(npt)

c    INTEGER nn, npt

DATA CON/10.0D0/

DATA RCP/1.D07/,TC/0.0/,TI/200.0/,L/0.02/

c----- calculul pasului in spatiu (DX)

DX = L/(NN-1)

write(*,*)'DX',DX

c----- calcul difuzibilitatii thermice (ALFA) si criteriului de stabilitate (CRS)

ALFA = CON/RCP

write(*,*)'alfa con',alfa,con

CRS = (DX**2)/alfa/2.0

write(*,*)'CRS',crs

c-----initializarea pasului de timp cu valorile CRS

c    DT = aint(CRS/6.0)

c------ pasul de timp-------- ----- ------ -------

DT = crs

if (DT. lt. 10 .and. DT .gt. 1.0) then

DT = 0.1

else

if (DT .lt. 1.0 .and. DT .gt. 0.1) then

DT = 0.01

else

if (DT .LT. 0.1 .and. DT .GT. 0.01) then

DT = 0.001

else

if (DT .LT. 0.01 .and. DT .GT. 0.001) then

dt= 0.0001

else

if (dt .lt. 0.001 .and. dt .gt. 0.0001) then

DT = 0.00001

endif

endif

endif

endif

endif

c-------- ----- ------ ----- ----- ----

c    dt=2.0

write(*,*)'dt=',dt

stop

c------initializarea conditiilor Dirichlet la x = L

do i=2,npt+1

TEMP(i,nn) = TC

enddo

c-----initializarea conditiilor in tot domeniul----- ----- -----------

do j=1,nn

TEMP(1,j) = TI

enddo

c-----formarea vectorului pentru punctele de calcul----- ----- --------

AX(1)= 0.0

do j=1,NN-1

AX(j+1)= AX(j) + DX

enddo

write(*,*)'dx',dx

c-------BUCLA pentru calculul pasului in timp----- ----- --------

do i = 1,npt

c-------bucla in spatiu

ap = rcp*DX/(2*DT)

ap0 = ap

ae = con/DX

write(*,*)'ap ap0 ae',ap,ap0,ae

write(*,*)'rcp dx dt con',rcp,dx,dt,con

TEMP(i+1,1) = (ae*TEMP(i,2) + (ap0-ae)*TEMP(i,1))/ap

do j=2,NN-1

c--------calculul pasului ----- ----- ----- ----- ----

if (j .eq. nn-1) then

ap = rcp*DX/DT

ap0 = ap

aw = con/DX

ae = con/DX

write(*,*)'ap ap0 aw ae',ap,ap0,aw,ae

TEMP(i+1,j) = (aw*TEMP(i,j-1) + (ap0-aw-ae)*TEMP(i,j)

* + ae*TC )/ap

else

ap = rcp*DX/DT

ap0 = ap

aw = con/DX

ae = con/DX

TEMP(i+1,j) = (aw*TEMP(i,j-1) + ae*TEMP(i,j+1)

* + (ap0-aw-ae)*TEMP(i,j))/ap

endif

enddo

enddo

c--------- scrierea solutiei -------- ----- ------ ---------

open(20,file='apl4.prn')

write(20,*)'# solution VF -explicite'

write(20,*)'# DT = ',DT,'s'

write(20,*)'# DX = ',1000*DX,'mm'

do i=1,npt+1

write(20 ,*)'# npt=',i-1, ' t=',(i-1)*dt,' s'

do j=1,nn

write(20,101)1000*ax(j),temp(i,j)

enddo

endoo

open(20,file='REFERAT 4.prn')

write(20,*)'# solution VF -explicite'

write(20,*)'# DT = ',DT,'s'

write(20,*)'# DX = ',1000*DX,'mm'

do i=1,npt+1

IF (i.eq.npt+1) the

c----- ----- --------SCRIEREA SOLUTIEI----- ----- --------- ----- -------

open (20,FILE=REFERAT 5).PRN')

do J=1,NN

write(20,101)AX(J),TEMP(I,J)

enddo

CLOSE (20)

FORMAT (F6.3,5X,F8.4)

else

write(20 ,*)'# npt=',i-1, ' t=',(i-1)*dt,' s'

do j=1,nn

write(20,102)1000*ax(j),temp(i,j)

enddo

endif

enddo

close(20)

format(F5.2,5x,f7.3)

STOP

END