Semnale CSK

Semnale CSK

Semnalele prezentate pana acum folosesc pentru impulsul de semnalizare semnale de forma:

(5.103)

cu in cazul general de forma :

(5.104)

Din teoria transformatei Fourier si analiza spectrala a acestor semnale se constata ca cu cat functia s(t) are un numar mai mare de derivate continue si egale cu zero la capetele intervalului de definitie [-T, T] , cu atat atenuarea componentelor spectrale este mai mare si implicit diafonia in canalul adiacent este mai redusa (datorita interferentei intersimboluri mai redusa). Considerand prima derivata a semnalului s(t) :

(5.105)

si impunand conditia ca s(t) = 0 la capetele intervalului [ - T , T ], se obtine:

(5.106)

Impunand acum conditia ca , obtinem conditia necesara si suficienta pentru ca semnalul sa aiba derivata I-a egala cu zero la capetele intervalului :

(5.107)

Prin generalizare la un numar oarecare n de derivate continue si egale cu zero la capetele intervalului [ - T , T ] conditia necesara si suficienta devine :

(5.108)

Conform definitiei lui Reiffen & White, semnalele cu se numesc semnale CSK (Continuous Shift Keying) .Pentru semnalele de tip CSK faza se defineste in general ca:

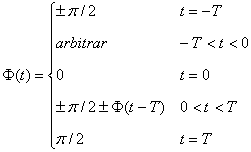(5.109)

adica are o variatie cu simetrie impara in raport cu momentul t = 0 .

Cateva exemple de semnale CSK sunt cele apartinand claselor:, s² (t) si CSK trapezoidal..

1.Clasa

Semnalele au forma generala de tipul:

(5.110)

cu de forma :

cu k impar. (5.111)

2. Clasa s² (t)

Semnalele au forma generala de tipul :

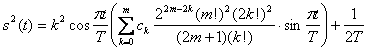(5.112)

Aceste semnale au primele m derivate egale cu zero la momentele

3.Clasa CSK trapezoidal

Frecventa semnalului CSK de acest tip variaza trapezoidal iar faza semnalului are o portiune de variatie liniara incadrata de doua portiuni parabolice.

Faza are forma de variatie:

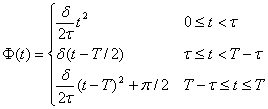(5.113)

cu

In afara de aceste trei tipuri de semnale CSK mai exista o clasa de semnale ce au forma generala:

(5.114)

si care indeplinesc conditiile definitiei Reiffen & White, deci intra in categoria semnalelor CSK (se poate arata ca cel putin primele cinci derivate sunt continue si egale cu 0 la capetele intervalului [- T , T ] ) .

Pentru a calcula densitatea spectrala de putere pornim de la forma in timp a semnalului s(t) si calculam mai intai transformata Fourier :

(5.115)

Pentru a simplifica programul de calcul se face schimbarea de variabila:

(5.116)

de unde se obtine:

(5.117)

Notand si tinand cont ca

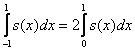(5.118)

deoarece s(x) este o functie reala si para, se obtine:

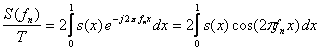(5.119)

Notand

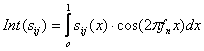(5.120)

se obtine pentru densitatea spectrala de putere expresia:

(5.121)