Calculul arborilor reductorului de turatie

Calculul arborilor reductorului de turatie

Arborii cutiilor de viteze sunt solicitati la incovoiere si rasucire (torsiune). Aceste solicitari dau nastere la deformatii elastice de incovoiere si torsiune, care daca depasesc limitele admisibile, conduc la o angrenare necorespunzatoare, modificand legile angrenarii si reducand gradul de acoperire.

3.1 Determinarea schemei de incarcare a arborilor si calculul reactiunilor din lagare

Fig. 3.1 Schema de incarcare a arborilor

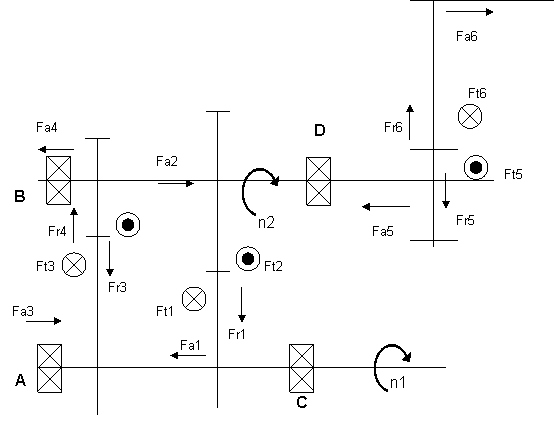
Incarcarile arborilor cutiilor de viteze sunt determinate de fortele din angrenajele rotilor dintate. Aceste forte dau nastere la reactiuni corespunzatoare in lagarele arborilor, a caror determinare este necesara atat pentru calculul de rezistenta al arborilor cat si pentru calculul de alegere al rulmentilor. Fortele care actioneaza in fiecare angrenaj sunt:

Fortele tangentiale:;

Fortele radiale: ;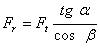

Fortele axiale: , unde:

i_k este raportul de transmitere de la motor la roata pentru care se determina fortele;

α_t este unghiul de angrenare;

β este unghiul de inclinare al danturii;

r_d este raza cercului de divizare al rotii;

6.3.1.1 Schema de incarcare a arborelui primar

In figurile 3.2 si 3.3. se prezinta schemele de incarcare ale arborilor in cazul obtinerii treptei de viteza k. Arborele primar al cutiei de viteze cu doi arbori este solicitat de fortele care apar intr-un singur angrenaj. Deoarece asupra arborilor actioneaza forte in plane diferite, acestea se descompun in componente continute in planul format de axele arborilor primar si secundar si in componente perpendiculare pe acest plan; planul format din axele arborilor cutiei de viteze este un plan vertical, motiv pentru care fortele se descompun in componente verticale si orizontale.

La stabilirea reactiunilor se considera arborele in echilibru static sub actiunea fortelor F_t, F_a si F_r. Sensul fortei axiale depinde de unghiul de inclinare a danturii.

Deoarece la schimbarea treptelor de viteza se modifica atat fortele cat si pozitia rotilor active in raport cu reazemele, se schimba si reactiunile in lagare, ceea ce impune ca determinarea lor sa se faca pentru fiecare treapta de viteza.

Pentru calculul reactiunilor este necesar sa se cunoasca dimensiunile prezentate in figurile 3.2. si 3.3., astfel:

L₁ - distanta dintre lagarele anterior si intermediar, intre care sunt montate pinioanele conducatoare pentru treptele de viteza;

L₂ - distanta dintre lagarele anterior si intermediar, intre care sunt montate rotile conduse pentru treptele de viteza;

l₁ - distanta dintre axa de simetrie a pinionului conducator al treptei I si axa de simetrie a lagarului anterior;

l₂ - distanta dintre axa de simetrie a pinionului conducator al treptei I si axa de simetrie a lagarului posterior ( sau intermediar);

l₃ - distanta dintre axa de simetrie a pinionului de atac al transmisiei principale si axa de simetrie a lagarului anterior al arborelui primar;

In cazul arborelui secundar l₁ si l₂ devin l₄ respectiv l₅;

De regula l₁ = l₃, l₂ = l₄ si L₁ = L₂;

Pentru cutia de viteze aleasa ca solutie de proiectare aceste distante se adopta astfel:

L₁ = L₂- pentru treptele I-II;

l₁ = 19.75 mm - pentru treapta I; si 17 mm pentru treapta II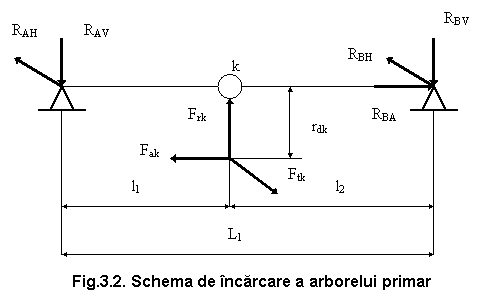

Fiind cunoscute dimensiunile geometrice ale cutiei de viteze se pot calcula reactiunile din lagarele arborelui primar, astfel:

Reactiunile in plan orizontal :

- reactiunea in plan orizontal din lagarul anterior;

- reactiunea in plan orizontal din lagarul intermediar

Reactiunile in plan vertical :

- reactiunea in plan vertical din lagarul anterior

- reactiunea in plan vertical din lagarul intermediar

- reactiunea produsa de forta axiala in lagarul intermediar;

Reactiunile totale din lagare:

- reactiunea totala din lagarul anterior;

- reactiunea totala din lagarul posterior;

3.3. Schema de incarcare a arborelui secundar

Arborele secundar este solicitat de fortele care apar in angrenajul cu arborele primar si de fortele din transmisia principala. Schema de incarcare a arborelui se prezinta in figura 3.2 iar rezultatele obtinute in urma unui calcul numeric sunt sistematizate in tabel .

Reactiunile din lagarele arborelui secundar sunt date de relatiile:

Reactiunile in plan orizontal :

;

Reactiunile in plan vertical :

;

;

Reactiunile totale din lagare:.

;

.3.2 Predimensionarea arborilor din conditii de rezistenta la solicitarile de incovoiere si torsiune

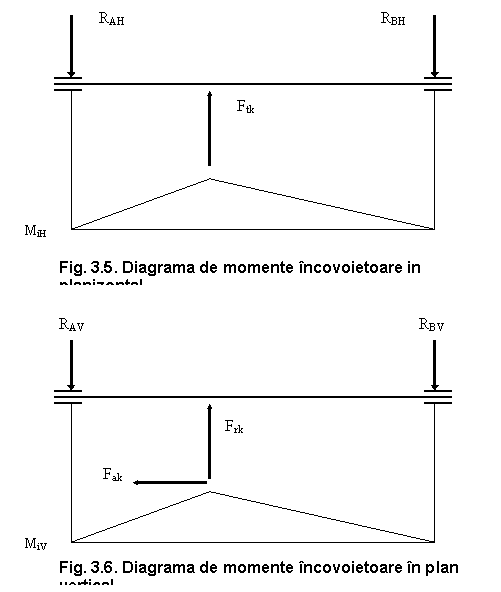
Cunoscandu-se reactiunile din lagare R_V si R_H si distantele dintre rotile dintate si lagare, se determina momentele de incovoiere maxime in plan orizontal si vertical, in dreptul rotilor dintate (fig. 6.21 si 6.22):

3.2.1.Arborele primar

Momentul incovoietor maxim in plan orizontal:

Momentul incovoietor maxim in plan vertical:

Momentul incovoietor rezultant:

3.2.2.Arborele secundar

Momentul incovoietor maxim in plan orizontal:

Momentul incovoietor maxim in plan vertical:

Momentul incovoietor rezultant:

Pentru arborii cutiei de viteze, solicitati la incovoiere si torsiune, efortul unitar echivalent se determina dupa ipoteza a III-a de rupere cu relatia:

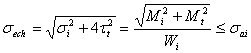
unde:

este efortul unitar de incovoiere;

este momentul incovoietor rezultant;

este modulul de rezistenta la incovoiere;

este momentul de torsiune;

este modulul de rezistenta la torsiune;

este momentul de torsiune ;

este raportul de transmitere dintre motor si arborele care se calculeaza;

Diametrul arborilor se determina din relatia: .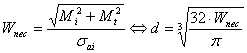

3.3. Calculul de verificare a rigiditatii arborilor

Solicitarile compuse de torsiune si incovoiere ale arborilor dau nastere la deformatii elastice care, daca depasesc anumite valori admisibile, conduc la o angrenare necorespunzatoare, iar solicitarile danturii cresc. Datorita deformatiei arborilor polul angrenarii, osciland in jurul pozitiei teoretice, determina o miscare neuniforma a arborelui condus, fapt ce implica o functionare zgomotoasa.

Sageata totala a arborelui, in locul de dispunere a rotii dintate, se determina cu relatia:

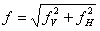
unde:

f_V este sageata in planul vertical (datorita fortelor F_r si F_a );

f_H este sageata in planul orizontal ( datorita fortei F_t );

In figura 3.5. se prezinta schema de incarcare a arborilor.

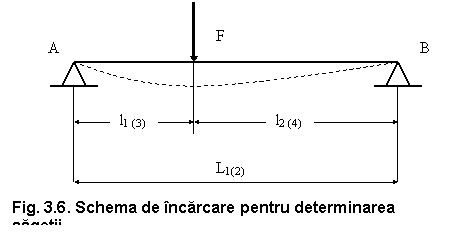
Sageata in plan orizontal, in dreptul rotilor dintate din angrenajul treptei k, este:

, pentru arborele primar;

, pentru arborele secundar,

unde:

E este modulul de elasticitate longitudinal;

este momentul de inertie axial;

D este diametrul arborelui;

Sageata in plan vertical este:

, pentru arborele primar;

, pentru arborele secundar;

In cazul cutiilor de viteze pentru autoturisme, sageata totala admisibila ( in planul de dispunere al rotilor), considerand incarcarea corespunzatoare momentului motor maxim este: f = 0,13 - 0,15 mm pentru treptele superioare; f = 0,15 - 0,25 mm pentru treptele inferioare.

Din cele expuse in randurile de mai sus, se observa ca ne intereseaza care este sectiunea periculoasa, care este deformarea maxima a arborelui, cat s-a rotit acesta in urma solicitarii la care a fost supus si daca materialul rezista la incarcarea la care a fost supus.

Am folosit un program specializat in calcule tehnice, Mechanical Desktop, in urma generarii conturului arborilor si stabilirii punctelor de reazem (locurile unde sunt pozitionate lagarele), dupa incarcarea cu momente de torsiune dupa fiecare arbore, au rezultat diagramele de momente incovoietoare echivalente, diagramele de momente de torsiune, sagetile maxime si unghiul de rotatie al arborelui reductorului.